基于CFD的斜航船舶浮态数值预报

邵江明，应业炬

(浙江海洋学院船舶与海洋工程学院，浙江舟山 316022)

基于CFD的斜航船舶浮态数值预报

邵江明，应业炬

(浙江海洋学院船舶与海洋工程学院，浙江舟山 316022)

目前涉及斜航船舶的数值模拟计算鲜有在模拟过程中考虑到船舶浮态的影响，然而浮态变化对水动力数值计算精度的影响是不容忽视的。基于此，文章以系列60船斜航运动（傅汝德数Fr=0.316，斜航角β=10°）为算例，采用重叠网格技术处理斜航船的大幅运动问题，通过耦合求解船舶六自由度运动方程和流体流动方程的方法，计算出了斜航船的升沉量、纵倾和横倾角度。结果显示，考虑浮态的数值预报结果与爱荷华大学的试验数据相比误差基本控制在10%以内，体现出该数值计算预报方法具有较强的工程实用性。

斜航；浮态计算；重叠网格；数值模拟

船舶斜航即指船舶的航行方向与前方来流形成一定夹角的航行状态，水面船舶大多数情况下都处于斜航状态。当船舶斜航时，受到不对称流的影响，船体受到较直航情况更加复杂的水动力影响。比如，在流场方面：斜航船的尾流场中流体分离作用更加明显，伴流分数变大[1]；浮态方面，斜航船除了会出现升沉、纵倾运动外往往还会出现较为明显的横倾。横倾作用对高重心船（集装箱船或者滚装船）的影响是非常恶劣的，它可能导致货物碰撞甚至倾覆。因此对斜航船浮态的研究显得格外重要。

目前对船舶斜航的研究主要有约束模试验[2-3]、基于势流理论的理论计算[4-5]和和基于黏性流理论数值模拟[6-7]。约束模试验方法具有一定的精度优势，但一般费时费力。基于势流理论的计算对受黏性影响较大的运动很难模拟准确，比如横倾运动。近些年来，随着计算机科学技术的飞速发展，基于计算流体动力学（CFD）的数值模拟方法得到越来越广泛的应用，模拟中引入湍流模型概念充分考虑到流体的黏性作用。目前，这种方法已成为与约束模试验并驾齐驱、相辅相成的一种水动力预报方法。回顾以往对船舶斜航的数值模拟，可以发现，在绝大部分的研究中很少在模拟中考虑到船舶浮态影响。然而，浮态对水动力计算精度的影响是不容忽视的。刘晗，马宁等[8]在对比由Fluent软件计算得到的斜航KVLCC2船模水动力的数值结果和由循环水槽平面运动机构试验得到的试验结果中发现，在斜航角为20度时，不考虑浮态情况下的水动力系数同试验值误差达到20%之多。邹璐[9]在研究数值计算精度中提到，对比考虑斜航船舶升沉、纵倾后的水动力计算值和不考虑浮态改变的情况，误差在20%-25%之间。

在本文的数值模拟中，采用Star-ccm软件，通过耦合求解船舶的运动方程和流体运动方程，计算出了斜航船的浮态变化，其中包括升沉、纵倾以及横倾。计算结果同爱荷华大学的实验进行对比，吻合良好。

1 数学模型

1.1 流体运动方程

连续性方程：

动量方程：

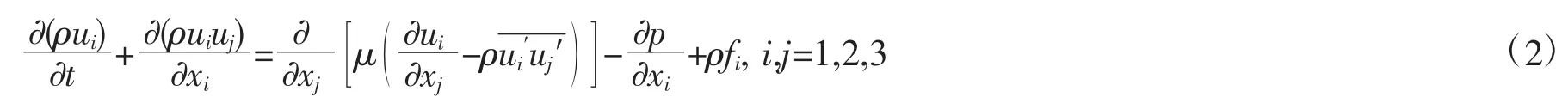
对湍流的模拟采用雷诺平均法可得：

式中：ui，uj为速度分量；P为流体压力；μ为动力粘性系数；fi为坐标变换引起的惯性力，其中是随船坐标系下的线速度和角速度是随船坐标系下的位置矢量(xs,ys,zs);Ui是斜航特征速度。自由液面采用流体体积函数VOF方法来追踪自由液面的运动状态：

式中：aq是某计算单元内第q相流体占的体积分数；ρq是第q相的密度。

文中选用SST k-ω湍流模型来封闭控制方程；微分方程的离散采用有限体积法；对流项采用二阶迎风差分格式；湍动能及其耗散、体积分数都采用二阶迎风格式；扩散项采用中心差分格式；压力和速度耦合采用PISO方法。松弛因子除了压力项都选用0.3，压力项用0.1。时间积分采用二阶欧拉隐士格式，时间步长取为0.002 s，内部迭代10次。

1.2 船舶运动方程

云南电力市场中，对具有年调节能力以上的机组的调节电量有一定的政策倾斜。具有年调节能力及以上水库的水电厂(小湾、糯扎渡、龙江、马鹿塘、普西桥、泗南江、小中甸)的调节电量(年设计电量的25%，枯水期每月分配年调节电量的10%，丰水期每月分配调节电量的6%)按照核定的上网电价。且接入500 kV电网的大型水电机组参与西电东送摘牌，价格在0.24～0.25元/kWh之间，高于市场电价。即云南已对省内有调节能力和大型的水电机组进行了一定的政策倾斜。

根据刚体六自由运动方程理论，推知船舶的六自由度运动包括重心的平动和绕重心的转动。船舶的线加速度和角加速度可以分别通过动量定理和动量矩定理求得，如下：

2 算例描述

本文选取系列60船模作为算例。国际拖曳水池会议(ITTC)在1996年把系列60船列为CFD计算船舶阻力和推进的标准船型。它的主尺度如表1所示。采用双重坐标系来描述斜航船舶的浮态，即惯性坐标系和随船坐标系，如图1所示。随船坐标系的原点位于船模重心位置，x轴指向船首方向，y轴指向左舷，z轴指向垂直甲板方向向上。欧拉角φ、θ、ψ分别表示横倾角、纵倾角和艏摇角，规定向右舷侧转向的横倾角为正，抬艏的纵倾角为正，升沉量为正表示船舶上浮，斜航角β以偏向右舷侧为正。

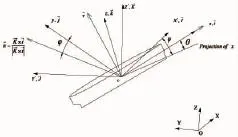
图1 坐标系Fig.1 Coordinate system

表1 系列60实船、船模主要参数Tab.1 Parameters of series 60 ship and model

3 数值计算

3.1 计算方法

要计算出斜航船的浮态变化，这需要耦合求解船舶的六自由度运动方程和流体流动方程。大致步骤如下：

1）RANS求解器求解船舶周围流场，通过积分船表面法向和切向应力得到作用在船上的力和力矩；

2）把第一步中求得力和力矩输入到六自由度求解器中计算出船的加速度、速度和位移；

3）更新船舶浮态，再一次重复第一、二步，直至浮态不再发生变化。

3.2 计算域和边界条件

计算域及其边界条件设置如图2所示。入流边界位于距离船首1.5倍船长位置；左舷侧的远场边界距离左舷侧1.5倍船长；右舷侧的出流边界距离右舷侧2.5倍船长；出流边界距离船尾2.5倍船长，其上设置压力出口边界条件，且P=0。船表面设置为不可穿透无滑移边界条件，为了避免甲板上浪，干舷被加高1.5倍吃水，上表面距离加高后的甲板1倍船长；文中模拟无限水域中的斜航情况，水底距离水面1.5倍船长。在入流边界、远场边界、上表面和水底设置为速度进口边界条件，且速度为u=-Ucosβ，v=-Usinβ，w=0，式中，u，v，w为速度分量，U为斜航特征速度。

图2 计算域及其边界条件Fig.2 The computational domain and boundary conditions

3.3 计算网格

重叠网格拥有网格逻辑关系简单，流场计算精度高、效率高、壁面粘性模拟能力强等优点，更弥补了结构网格[10]对外形适应能力差的缺点，相比较于传统的网格生成方法，重叠网格更易于生成高质量网格，对大幅度运动的斜航船浮态求解精度较高。本文中采用重叠网格来划分流场，网格划分如图3所示，用重叠网格将流动区域分为两个子区域，即背景网格区域和重叠网格区域，两个子区域内网独立生成，彼此存在重叠关系，在重叠区域内流场信息通过插值进行数据交换。重叠网格可以在背景网格中作大幅运动而不会出现网格变形和重生成，保证了斜航船大幅度运动时的网格质量。图3（a）中贴近船舶周围最内层颜色最深长方形部分为重叠网格区域，网格密度从里到外由高到低平滑过渡。在船舶斜航中，船两侧的波浪是不对称的，文中在自由液面附近，采用两边不对称的四面体加密区域（如图3（a）所示）来捕捉船行波。此外，船附近生成边界层网格以更加准确地求解流场。

图3 网格划分Fig.3 Grid generation

4 计算结果分析与讨论

图4，图5分别展示了Fr=0.316,β=10°时升沉、纵倾、横倾时历曲线和总阻力系数（CT）、侧向力系数(CS)、艏摇力矩(CM)系数时历曲线，其中横坐标均为时间（s），纵坐标为无量纲数值。为了同爱荷华大学的试验数据进行直接对比，将总阻力、侧向力和首摇力矩进行无量纲化，无量纲化方法如式（9）-（11）。

本文中定义一个比较误差，具体为：E%D=100*(S-D)/D，式中，S为计算值，D为试验值。从图4看出除了横倾角以外，其他考察的物理量都能在很短的时间内收敛到一个稳定值。横倾角以一种衰减的形式逐步达到稳定。横倾角、纵倾角，升沉量都为负，这表明斜航船处于向左舷侧（迎风面）横倾、埋首和下沉的状态。横倾角、纵倾角、升沉、总阻力系数、侧向力系数和艏摇力矩系数同爱荷华大学试验数据的比较结果如表2所示，误差分别为-7.35、+6.8、-8.75、-4.93、-4.64和+4.81，浮态计算值基本控制在±10%以内，总体上可以满足实际工程需要。

表2 浮态计算结果同实验数据对比Tab.2 Comparisons between Computational result with experimental data

值得注意的是，侧向力计算误差为4.64%，之前的学者，比如CuraHochbaum[11]、Rodrigo Azcueta[12]在数值模拟斜航问题时，侧向力的计算误差都达到了25%量级，其中CuraHochbaum把侧向力误差偏大归结于在他的计算中没有考虑自由液面和没有计及浮态的影响，本文的侧向力计算精度有了很大的改善。

船模试验中只有不考虑浮态的波高图可供参考，本文中将不考虑浮态的计算波高、考虑浮态的计算波高分别同不考虑浮态的试验波高进行对比，如图6所示。不考虑浮态的计算波高（b）同试验（a）相比很接近，出现在船首的最大波高同试验值基本保持一致，出现在肩部的最小波高计算值比试验值略大。在考虑浮态的后的波形变化，对比试验波高图，最大波高抬高了3%，而波谷降低了34%。最大波峰依然出现在船首迎风面，最大波谷出现在船的肩部。波形变化不大，这包括波包角、散波角和尾流场中的楔形角，只是波浪衰减的比较厉害，主要是由于网格离船越远，密度越低造成的。

图4 升沉、纵倾、横倾时历曲线图Fig.4 Curves of sinkage、trim and heel

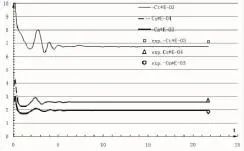
图5 总阻力系数、侧向力系数、艏摇力矩系数时历曲线Fig.5 Coefficients curves of resistance、lateral force and yawing moment

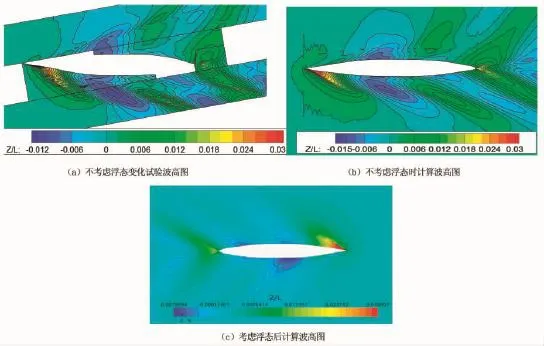
图6 计算波高同试验波高对比Fig.6 Comparisons between Computationalwave height with experimental wave height

船体表面动压分布情况如图7所示。通过计算结果可知船首迎风面压力大于背风面，而船尾两侧压力变化不明显，由于两侧压力差产生了转首力矩。迎风面底部压力大于背风面压力，这导致了船向迎风面横倾。横倾的同时也出现了首倾现象，这导致了船首底部压力大于船尾压力的情况。

图7 船体表面动压分布Fig.7 Dynamic pressure contours at hull surface

图8展示了船舯横剖面上Z向速度计算同试验结果的对比图。图8(a)可以明显地看出船有一个向左舷侧横倾的状态，这造成了船舭部形成了明显的涡。同试验对比可以看出计算的负涡核心筒试验比较接近，但是正的涡核心位置差别较大，试验中的正涡核心远离船体，出现流体分离现象，而计算中的正涡核心也有远离船体的趋势但还没有远离。这也可能是造成侧向力以及升沉误差较大的原因。此外，最大的速度偏低了11%，最小速度偏高了5%。总体而言，采用本文中的重叠网格技术可以较为准确地预报斜航船舶周围流场。

图8 计算船舯横剖面速度云图同试验对比Fig.8 Amidships cross-sectional velocity contours compared with experiment data

5 结语

本文给出了一种基于CFD理论进行斜航船舶浮态数值预报的方法。采用重叠网格技术，通过耦合求解流体运动方程和船舶六自由度方程的方法，计算出了系列60船在傅汝德数Fr=0.316和斜航角β=10°情况下的斜航船浮态，包括升沉、纵倾和横倾等。计算显示采用重叠网格能很好的处理斜航船大幅运动问题，计算中网格不变形和重生成充分保障了网格质量，而这些都保证了计算精度。将计算结果同爱荷华大学的试验数据进行对比，偏差基本控制在10%以内，吻合较好，体现出该方法具有较强的的工程实用性。文中展示了部分斜航船周围的流场信息包括波高图和舯横剖面速度云图，计算结果较为准确的预报了斜航船周围流场变化，对理解斜航船浮态变化机理有一定的帮助。

[1]郭春雨,赵庆新,赵大刚.基于CFD仿真模拟的船模自航试验数据处理[J].船海工程,2013,42(3):17-20.

[2]OKUNO T,TANAKA N,HASEGAWA Y.Flow field measurements around ship hull at incidence[J].J Kansai Soc Naval Arch, 1989,212:67-74.

[3]LONGO J,STERN F.Effects of drift angle on model ship flow[J].Experiments in Fluids,2002,32:558-569.

[4]INOUE S,HIRANO M,KIJIMA K.Hydrodynamic derivatives on ship manoeuvring[J].International Shipbuilding Progress,198, 28(321):112-125.

[5]YUKAWA K,KIJIMA K.An estimation of hydrodynamic forces acting on a ship hull in manoeuvring motion[J].Trans West-Japan Soc Nav Arch,1998,95:67-79.

[6]TOXOPEUS S,SIMONSEN C D,GUILMINEAU E,et al.Viscous-flow calculations for KVLCC2 in manoeuvring motion in deep and shallow water[C]//NATO AVT-189 Specialists Meeting on Assessment of Stability and Control Prediction Methods for NATO Air and Sea Vehicles.Portsdown West,UK,2011:151-169.

[7]WANG H M,ZOU Z J,TIAN X M.Computation of the viscous hydrodynamic forces on a KVLCC2 model moving obliquely in shallow water[J].Journal of Shanghai Jiaotong University,2009,14(2):241-244.

[8]刘 晗,马 宁,邓德衡,等.循环水槽在平面运动机构试验中的应用及其数值验证 [C]//2013年船舶水动力学学术会议, 2013:623-631.

[9]邹 璐.浅水中低速斜航运动船舶水动力预报及误差分析[C]//2013年船舶水动力学学术会议,2013:503-510.

[10]王留洋,陈晓亮.瓯江口波流耦合作用下二维流场数值模拟研究[J].船海工程,2013,42(5):130-137.

[11]CURAHOCHBAUM A.Computation of the turbulent flow around a ship model in steady turn and in steady oblique motion[C] //Proc.22nd Symp on Naval Hydro,Washington,D.C.,USA,1998:198-213.

[12]AZCUETA R.Computation of turbulent free-surface flows around ships and floating bodies[J].Ship Technology Research, 2002,49(2):46-69.

CFD Theory Based Floating State Prediction of Oblique Ship Motion

SHAO Jiangming1，YING Yeju1，ZHOU Qi2,SUN Xiangjie3
（1.School of Naval Architecture&Ocean Engineering,Zhejiang Ocean University,Zhoushan,316022；2.Zhoushan Wonderful Marine Design CO.LTD.，Zhoushan 316021；3.School of Naval Architecture& Ocean Engineering，Harbin Engineering University，Harbin 150001，China）

The oblique ship motion calculation is rarelyconsidering the effects of ship floating state.However,the change of floating state can not be ignored due to it’s great effect on numerical calculation precision. In this paper,the oblique motion of Series 60 ship model with Fr=0.316,yaw angleβ=10°is taken as example. The running attitudes including the sinkage,trim and heel are obtained by coupling the 6-DOF equations of ship motion with the Reynolds Averaged Navier-Stokes(RANS)equations.The overset grid method is adopted to deal with the sinkage,trim and heel in large amplitude.Comparisons between the numerical results with IWOA (The University of Iowa)experimental data are made,and it is observed that the prediction error can be controlled bellow 10%,which successfully validates the applicability and efficiency of the proposed method in engineering applications.

Oblique Motion；Running Attitude；Six-DOF Equation；RANS

U661.3

A

1008－830X(2015)06－0559－06

2015-08-20

邵江明（1990-），男，硕士研究生，主要从事船舶水动力研究和船型优化设计.