基于ESTAR模型的单位根检验——Wald统计量的研究

胡俊娟

(浙江科技学院 理学院,杭州 310023)



浙江科技学院学报,第27卷第1期,2015年2月

Journal of Zhejiang University of Science and Technology

Vol.27 No.1, Feb. 2015

基于ESTAR模型的单位根检验——Wald统计量的研究

胡俊娟

(浙江科技学院 理学院,杭州 310023)

摘要:已有的基于ESTAR模型的单位根检验通常假设α=0,但实践研究表明α显著。对α≠0的情况进行单位根检验,研究该情形下的Wald检验统计量。从理论上推导了Wald检验统计量的极限分布,并通过Monte Carlo随机模拟,结果表明该统计量有效。

关键词:单位根检验;Wald统计量;ESTAR模型

自Teräsvirta[1]提出STAR(smooth transition autoregressive)模型以来,非线性模型一直受到国内外学者的关注。STAR模型很好地描述了模型的状态转化和结构变化,因而被广泛地应用于预测工业产出、实际汇率、失业率等主要宏观时间序列[2-3]。由于模型拟合前需要进行单位根检验,众多学者对指数STAR(ESTAR)模型进行了研究。Kapetanios等[4]提出了Dickey-Fuller型t统计量，Kruse[5]用修正的t统计量进行了研究，Hanck[6]对带均值的情况进行了研究。这些检验都在假设α=0的情况下进行,但实践研究表明α显著[7]。笔者在此基础上放宽了条件,在α≠0的情况下进行单位根检验的研究。

1基于ESTAR模型的单位根检验

ESTAR模型是STAR类模型中最常用的模型之一,首先给出ESTAR模型的具体形式:

yt=βyt-1+γyt-1G(yt-1;θ)+εt,t=1,…,T,

(1)

该过程也可以写成:

Δyt=αyt-1+γyt-1G(yt-1;θ)+εt,

(2)

式(2)中:α=β-1,Δ—差分算子。

1.1　Dickey-Fuller型t统计量

Kapetanios等[4]在假设α=0的条件下,考虑θ是否为零。即对于方程:

Δyt=γyt-1G(yt-1;θ)+εt

给出了原假设H0:θ=0,备择假设H1:θ>0来进行单位根检验。考虑到参数γ未知,常用的做法是用一阶泰勒展开来逼近非线性函数G(yt-1;θ),则检验方程就变成:

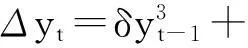
从而对方程检验H0:δ=0。Kapetanios等给出了Dickey-Fuller型t统计量:

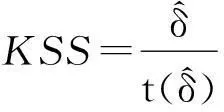
(3)

1.2　Wald检验统计量

考虑到ESTAR模型(式(1))中α不一定为零,则对ESTAR模型进行一阶泰勒展开后得到的辅助线性方程是:

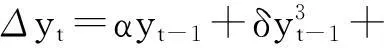
(4)

考虑到当α=δ=0时,模型含有单位根,所以对模型检验:H0:α=δ=0。

Wald检验是计量经济学三大检验方法之一,只要求计算无约束模型,在实证分析中得到广泛应用。在原假设H0:Rβ=0情况下的Wald统计量[8]为:

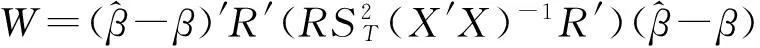
(5)

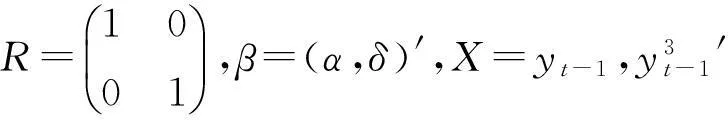
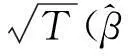
2Wald统计量的极限分布

为了给出统计量W的极限分布,先假设序列yt的六阶矩存在。有关W极限分布的定理如下。

定理1考虑模型(2)在H0:α=δ=0的条件下,统计量W有如下的极限分布:

W⟹A′B-1A,

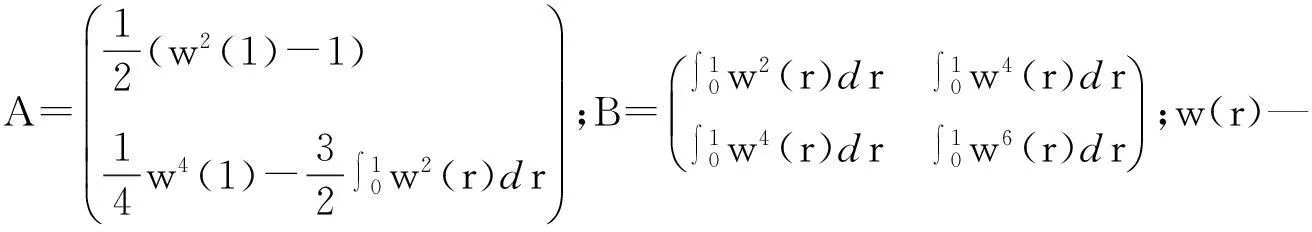
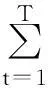
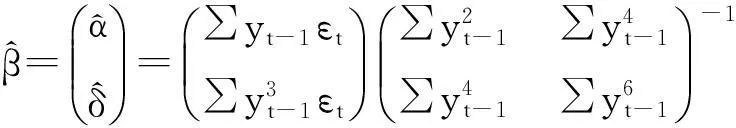
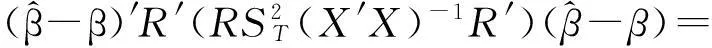
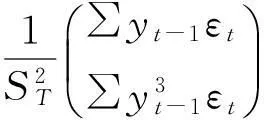
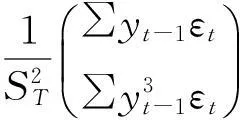
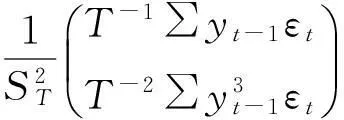
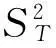
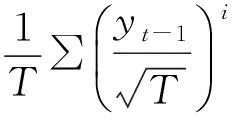
即

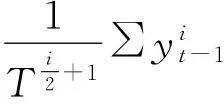
进一步,有:

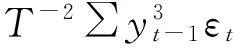
并且

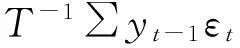
所以,可以得到:

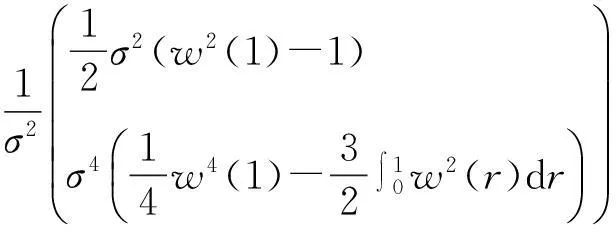
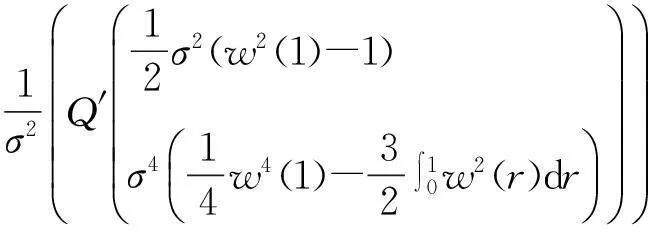
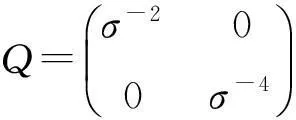
现对模型(2)进行推广,考虑误差项εt序列相关。根据ADF检验,通过加入p阶滞后项来代替误差项的序列相关,则模型(2)变成

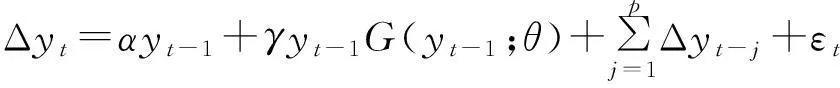
(6)

式(6)中:εt～i.i.d.(0,σ2)。则相应地可以得到辅助方程:

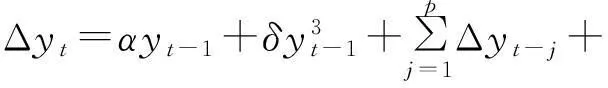
对于统计量W有如下分布:

定理2考虑模型(6)在H0:α=δ=0的条件下,统计量W有与定理1一样的极限分布。

证明:设T×p的数据矩阵Z=(ΔY-1,…,ΔY-p),其中ΔY-i=(Δy-i+1,…,Δy-i+T),设T×T矩阵M=IT-Z(Z′Z)-1Z′,向量ε=ε1,…,εT′,则

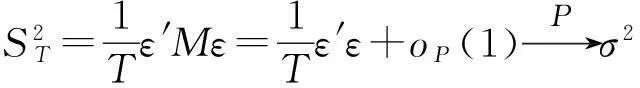
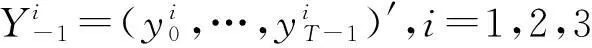
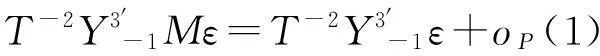
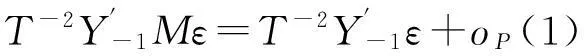
和

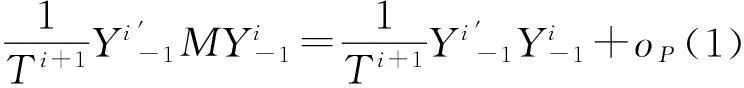
所以,类似地可以得到W⟹A′B-1A,

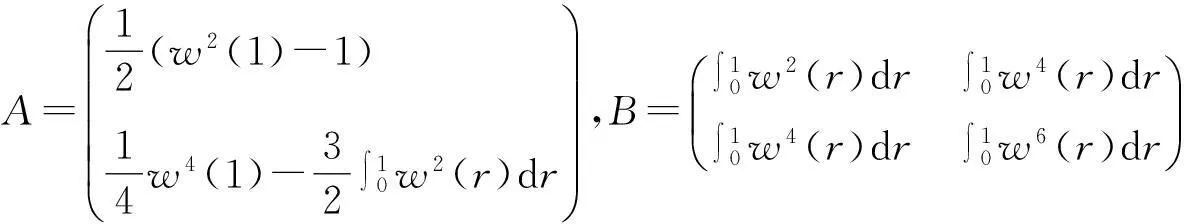
3Monte Carlo模拟

上述分析表明,在单位根检验下,参数约束的Wald统计量的极限分布都不是χ2分布。本研究采用蒙特卡罗模拟方法模拟出上述Wald统计量的临界值。数据生成过程为:Δyt=εt,y0=0,εt～i.i.d.(0,1)。考察统计量W的极限分布,样本容量T取1 000,针对样本容量模拟20 000次,从而得到检验统计量W常用检验水平0.01、0.05、0.10的渐进临界值(表1)。

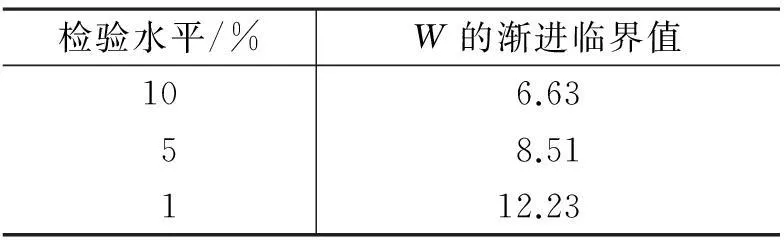
表1　统计量W的临界值

对于小样本而言,分别针对样本容量T为50、100、200，考察检验统计量的检验水平。数据生成过程为:Δyt=εt,εt=ρεt-1+ut,ut～i.i.d.(0,1)。为了考察更多情况,ρ取0~0.4的均匀分布。通过表2可以看出,统计量W的实际检验水平与名义检验水平一致。

表2　统计量W的实际检验水平

考虑数据生成过程为ESTAR模型,现对式(3)的统计量KSS和统计量W的势进行对比。不妨假设数据生成过程为:

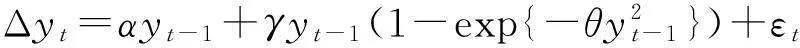
式中,α设为0.1,γ为-1.5、-1、-0.5,θ为0.001~0.01的均匀分布。给定名义水平为0.05,从表3可以看出,统计量W较统计量KSS有更高的势。

表3　统计量W和统计量KSS的势

4结语

本研究主要针对ESTAR模型提出用于单位根检验的Wald统计量,通过研究得出以下结论:无论是否有p阶滞后项,含有单位根约束条件的Wald统计量的极限分布均不服从χ2分布,而是服从以Wiener过程泛函表示的分布;蒙特卡罗模拟结果显示,有限样本下Wald统计量W的势比KSS的势更高,故认为统计量W更有效。

参考文献:

[1]Teräsvirta T. Specification, estimation and evaluation of smooth transition autoregressive models[J]. Journal of the American Statistical Association,1994,89:208-218.

[2]Lundbergh S, Teräsvirta T. Forecasting with smooth transition autoregressive models[M]. [S.L.]: Clements M P,2001.

[3]Van Dijk D, Teräsvirta T, Franses P H. Smooth transition autoregressive models: A survey of recent developments[J]. Econometric Reviews,2002,21:1-47.

[4]Kapetanios G, Shin Y, Snell A. Testing for a unit root in the nonlinear STAR framework[J]. Journal of Econometrics,2003,112:359-379.

[5]Kruse R. A new unit root test against ESTAR based on a class of modified statistics[J]. Statistical Papers,2011,52(1):71-85.

[6]Hanck C. On the asymptotic distribution of a unit root test against ESTAR alternatives[J]. Statistics and Probability Letters,2012,82:360-364.

[7]Ubilava D, Helmers C G. Forecasting ENSO with a smooth transition autoregressive model[J].Environmental Modelling and Software,2013,40:181-190.

[8]张凌翔,张晓峒.单位根检验中的Wald统计量研究[J].数量经济技术经济研究,2009(7):146-158.

[9]聂巧平,张晓峒.ADF单位根检验中联合检验F统计量研究[J].统计研究,2007,24(2):73-80.

Unit root test based on ESTAR process

—Study on Wald statistics

HU Junjuan

(School of Sciences, Zhejiang University of Science and Technology, Hangzhou 310023, China)

Abstract:The alternative hypothesis of exponential smooth transition autoregressive (ESTAR) nonlinearity usually assumes thatα=0, while the Existing tests of the unit root hypothesis is against that. However, empirical work indicates that the estimated value of α is always greater than zero and significant. Hence, the paper relaxes the restriction in the test regression and investigate the Wald-type test for a unit root process against ESTAR process. The asymptotic distributions of the test statistic are derived. Results show that the Wald statistic is effective via Monte Carlo simulation.

Key words:unit root test; Wald-type statistic; exponential smooth transition autoregressive

中图分类号:O212;F222

文献标志码:A

文章编号:1671-8798(2015)01-0006-05

作者简介:胡俊娟(1979—),女,浙江省兰溪人,讲师,博士研究生,主要从事时间序列分析研究。

收稿日期:2015-01-21

doi:10.3969/j.issn.1671-8798.2015.01.002