卡尔曼滤波在水下惯性导航系统中的研究及实现

雷曙光，张　柳，林列书

(广州民航职业技术学院，广东广州510403)

卡尔曼滤波在水下惯性导航系统中的研究及实现

雷曙光，张柳，林列书

(广州民航职业技术学院，广东广州510403)

摘要:首先建立惯性导航系统中的速度误差、位置误差、陀螺仪误差模型，然后与现实相联系研究带偏移量的卡尔曼滤波，同时对偏移量进行估计，最后通过实验验证卡尔曼滤波对航向、陀螺仪误差等的修正，极大地提高了水下惯性导航系统的结算能力和准确性。

关键词:卡尔曼滤波;惯性导航系统;偏移量;估计量

The research and implementation of kalman filtering in INS integrated navigation

LEI Shu-guang，ZHANG Liu，LIN Lie-shu
(Guangzhou Civil Aviation College，Guangzhou 510403，China)

Abstract:First，this article established speed error，position error，gyro error model in inertial navigation system．Then linked with reality and researched on Kalman filter with offsets．At the same time estimated offset．Finally，experiments show that Kalman filter amendmented to the heading，gyroscope error，etc．This algorithm greatly improved the billing capability and accuracy of underwater inertial navigation system．

Key words:Kalman filter; INS integrated navigation; bias federated filter;estimator

0　引言

随着科技的发展，利用导航对潜艇等非固定目标进行定位、定向等应用越来越广泛，在复杂的海洋中对潜艇进行高精度的导航定位可以有效的预防意外事故的发生。惯性导航系统全天候都可以工作，隐蔽性强、带宽宽，能够平稳的提供才捕捉到数据信息。在状态空间中卡尔曼滤波是典型的最优估计法。

本文首先建立了惯性导航系统中的速度误差、位置误差、陀螺仪误差模型，然后与现实相联系研究了带偏移量的卡尔曼滤波，同时对偏移量进行估计，最后通过实验验证卡尔曼滤波在水下惯性导航系统中的作用。

1　建立惯性导航系统的数学误差模型

在现实中船舶上的微机电系统在通电工作后，随着时间的增长，元件自身的温度会升高，同时环境、元件材质等影响使元器件的电压处在一个动态变化的状态，从而影响了惯性导航系统的精度，所以本文着重研究这种带有偏置的卡尔曼滤波，在利用卡尔曼滤波之前应该获取到惯性导航系统的数学误差模型。

惯性导航系统的误差有速度误差、位置误差、平台误差、陀螺仪和加速计等误差［1－3］。

1)陀螺仪误差方程

陀螺仪直接关系到惯性导航系统的姿态误差。本文选用的陀螺偏移模型是AIC最小的AR(1)。

将AR(1)的数学表达式xk=φ1xk－1+αk转换成连续的一阶马尔科夫x·(t) +βx(t) = z(t)，从而可以得到:

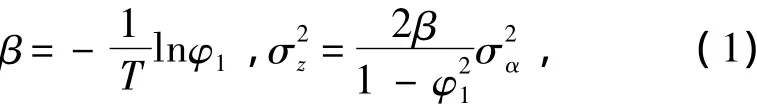
式中wg(t)为陀螺仪的随机信号。

2)位置误差模型

由

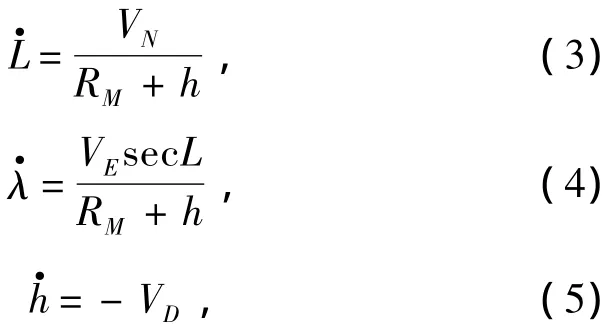
从而可以获得空间直角坐标的位置误差为:

3)航速误差

根据惯性导航方程

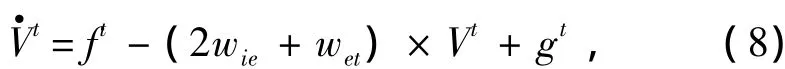
可知:

通常重力加速度被认为是常数，故σg= 0。令

则:

式中: fp为实际的加速度;Δp为测量的偏差。

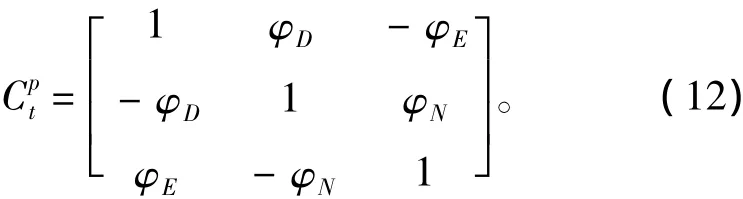
则:

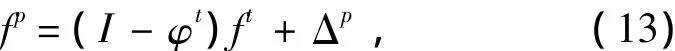
从而可得:

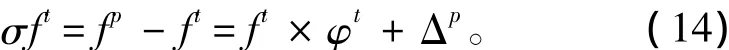
代入式(9)得到速度的误差方程:

2　带偏移量的卡尔曼滤波

参考文献根据［4］可知，带偏置的科尔曼滤波的估计状态方程为:

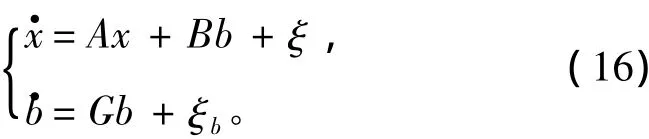
观测方程为:

对式(16)和(17)进行离散可得:

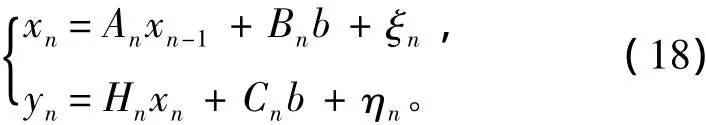
式中: xn为第n个更新点变化向量; yn为第n个更新点的观测向量; b为偏置向量; An，Bn，Hn，Cn均为随时间变化的矩阵系数;ξn为系统数学期望为0时的噪声;ηn为观测噪声。

在没有偏置的理想情况下，得到的状态方程为:

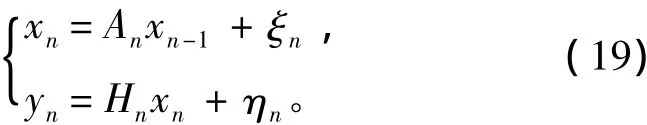
从而得到状态的估计方程为:

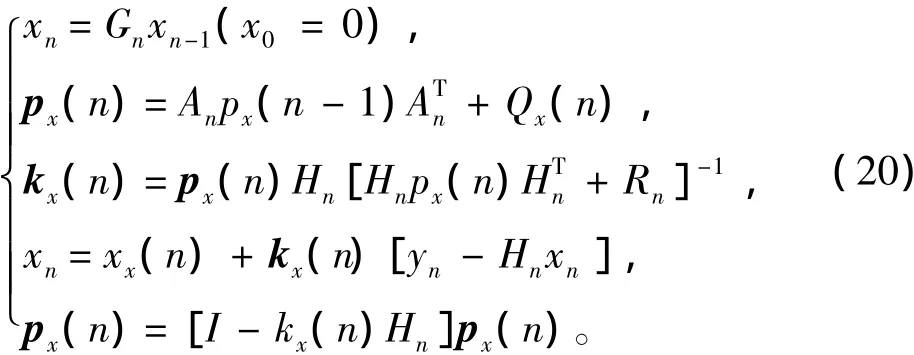
式中: x为理想状态下的估计; p为x的误差协方差矩阵; kx为卡尔曼滤波的增益矩阵。

当偏置已知时，b就是固定值，则可以得到x的估计:

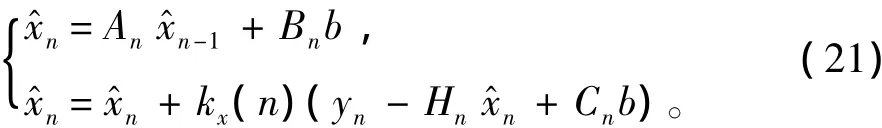
由式(20)和式(21)可得2个状态的估计值关系为:

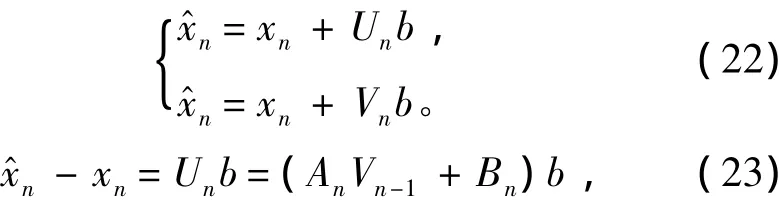
从而得到状态的加权阵:

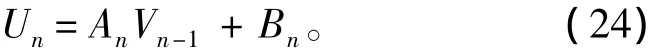
同时可知:

因此，可得关于每一步估计的状态矩阵:

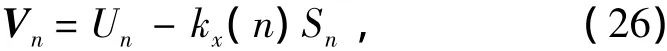
式中:

由式(24)～式(27)可以得到加权矩阵的类推方法。

没有偏置情况下，滤波器的测量误差为:

对上式作如下变换可得:

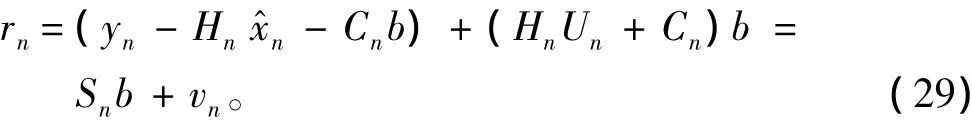
式中: vn为滤波估计的测量误差，表述了与自估计偏移量之间的关系; vn不是一个固定的值，因此测量值与估计值没有关系。

对偏移向量b进行估计:

式中: px和rn根据没有偏移量的情况估算求得; Sn通过式(24)～式(27)可得。

从而得到状态估计的修正值，利用式(30)修正没有偏移的x，从而得到最小方差估计表示为:

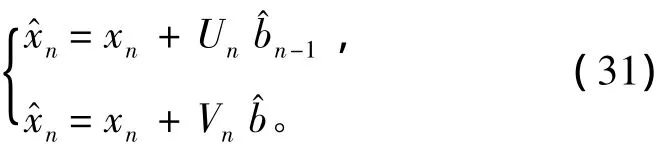
求偏移向量b的估计值

故而得到最小方差估计为:

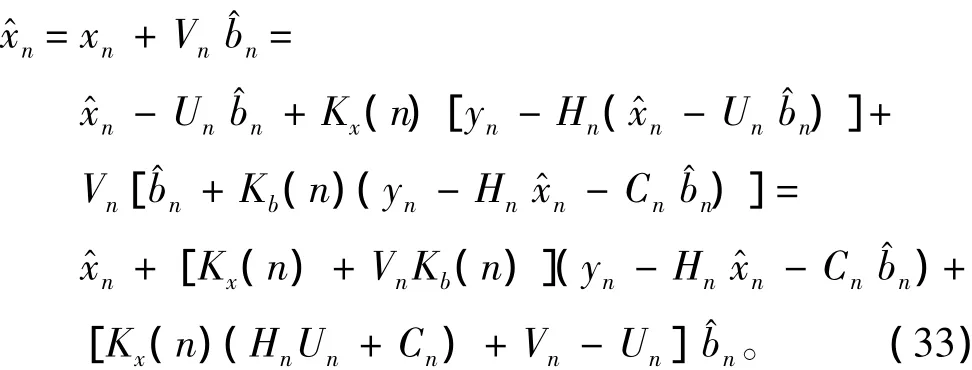
通过以上推理可知卡尔曼滤波是利用两部分之间的相互关系估算状态偏差。步骤如下估算出在偏移量作用下的，同时可以求得协方差矩阵P，P有系统状态X和b有关，根据二者影响的不同，可以将b对之的影响分离出来，从而求出偏移向量b。

3　带偏移的卡尔曼滤波在惯性导航系统的应用实验结果

本文通过建立六状态下的卡尔曼滤波方程估算航行方向、陀螺仪角速度等的误差。要估算的六状态误差为Δθ，Δγ，Δψ，Δwx，Δwy，Δwz。

由加速度计信号确定的姿态角θ0= 2.45°， γ0= 1.55°。令ψ0= 1°，从而获得初始姿态矩阵，实验结果如图1所示(横坐标表示时间，单位: s)。

图1　六个状态量的卡尔曼滤波误差曲线Fig.1　Kalman filter error curve of six state quantity

从图1可看出，航向角误差和姿态角误差在很短的时间内就接近于0，由此可知在经过卡尔曼滤波后，大大提升了系统的结算能力，并且准确度得以提高。角度的偏移量最大不超过±0.05°，一定时间后系统趋于平稳，从陀螺的角速度误差曲线可以看到处于稳定的状态。由此说明了带偏移量的卡尔曼滤波通过偏移量修正改善了实际应用中因为偏移量所带来的不准确性，提高了系统的稳定性。

4　结语

本文首先建立了惯性导航系统中的速度误差、位置误差、陀螺仪误差模型，然后与现实相联系研究了带偏移量的卡尔曼滤波，同时对偏移量进行估计，最后通过实验验证了通过卡尔曼滤波对航向、陀螺仪误差等的修正，极大提高了水下惯性导航系统的结算能力和准确性。

［1］LIU Hai-tao．Study and realization of the low-cost INS/GPS integrated navigation system algorithms［J］．Journal of Telemetry，Tracking and Command，2003，24(2) :36－41．

［2］WEN Wu．Federated filter of INS/GPS integrated navigation ［J］．Journal of North China Institute of Technology，2004，25 (4)．

［3］YAN Xian-gong．Research of kalman filter and its application in ship GPS/SINS integrated navigation［J］．Ship Science and Technology，2014，36(12) :128－131．

［4］BERNARD F．Treatment of bias in recursive filtering［C］/ / IEEE Transactions on Automatic Control，volAC－14，NO．4，AUGUST 1969:359－367．

作者简介:雷曙光(1973－)，男，副教授，研究方向为飞机电子设备维修研究。

收稿日期:2014－10－26;修回日期: 2014－12－27

文章编号:1672－7649(2015) 07－0200－03doi:10.3404/j.issn.1672－7649.2015.07.047

中图分类号:U665．26

文献标识码:A