基于改进混沌系统的微弱信号检测方法

石　敏，陈迎春，屈　武

(中国人民解放军91388部队，广东湛江524022)

基于改进混沌系统的微弱信号检测方法

石敏，陈迎春，屈武

(中国人民解放军91388部队，广东湛江524022)

摘要:混沌系统具有对噪声和与系统内置信号频差较大信号免疫，而对与系统内置信号频差较小信号敏感的特点，据此可检测强宽带噪声背景下的微弱信号。但在实际仿真过程中发现，当系统处于混沌临界状态时，输入纯噪声也可能引起系统的相变，且当输入的信号与系统内置信号频率相同而初相位不同时，可能不能引起系统的相变。这些情况的出现降低了微弱信号检测的正确率。本文主要针对该问题提出解决方法，将混沌系统内置信号的幅度取为小于混沌临界阈值，可避免纯噪声引起系统的相变，将混沌系统扩展为4种形式后，可检测不同初相位的输入信号。仿真结果证实该改进方法的有效性。

关键词:微弱信号检测;混沌;改进混沌系统

Weak signal detection method based on improved chaos system

SHI Min，CHEN Ying-chun，QU Wu
(No．91388 Unit of PLA，Zhanjiang 524022，China)

Abstract:Weak signal hides in strong broad band background noise can be detected by chaos system．It mainly bases on the characteristics that chaos system is immune to noise and signal whose frequency is quite different from that of inner signal in chaos system，while it is sensitive to the signal whose frequency is same as the inner signal's frequency in a chaotic system．But in the actual simulating process，it finds that pure noise inputs into chaos system which is under critical state will probably induce to system state variation．And signal whose frequency is same as inner signal while phase is different from inner signal inputs into chaos system which is under critical state，the system state variation will probably not happen．The appearance of these cases will reduce the detecting accuracy ratio of weak signal．The setting method is proposed in the paper to the question．The amplitude of inner signal in chaos system is chosen to less than the threshold of chaos critical state，which can avoid system state variation induced by pure noise．Expanding the chaos system to four forms can detect input signal with different original phase．Simulation results verify the validity of the improved method．

Key words:weak signal detection; chaos;improved chaos system

0　引言

传统的微弱信号检测方法大部分采用线性方法，在较低信噪比信号检测时存在不可避免的缺陷。利用非线性方法的混沌系统在微弱信号检测中表现出超常的优势，成为目前微弱信号检测方法研究中的一个热点［1－2］。其主要是基于混沌系统对噪声及与其内置信号频差较大信号具有免疫力，而对与混沌

系统内置信号差较小信号敏感的特点［3－8］。

实际仿真发现，当混沌系统处于混沌到大尺度变化的临界状态时，输入一定功率的纯噪声，也可能引起系统的相变［9－11］。且在混沌临界状态时，输入与其内置信号频率相同而初相位不同的信号时，也可能无法引起系统的相变。

针对混沌系统检测中出现的这些问题，本文采用改进的混沌系统进行微弱信号检测:将内置信号幅度取为小于临界阈值，可避免纯噪声引起的相变;将混沌系统扩展为4种形式后，可检测具有不同初相位的输入信号。

1　混沌系统微弱信号检测的基本原理

考虑可用于任意频率微弱信号检测的duffing混沌检测系统，其duffing方程为:

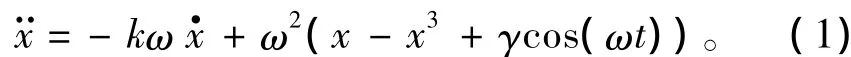
式中:ω和γ分别为混沌系统内置信号频率和幅度; k为阻尼系数，一般取k =0.5，(x－x3)为非线性项，x·和x··分别为x的一阶和二阶微分。

随着γ值的变化，系统的相轨迹将发生变化，当γ等于混沌临界阈值γd时，系统进入混沌临界状态。此时输入含有与内置信号频率相同的信号时，系统迅速从混沌状态转化为大尺度周期状态，而输入纯噪声时，系统仍保持混沌状态。据此可检测微弱信号是否存在。

2　混沌系统微弱信号检测中存在的问题

以ω=1为例，取系统初始值［x，x·］=［1，1］，根据Lyapunov指数或系统的相轨迹图得混沌临界阈值γd=0.827，图1分别给出了γ=0.827和γ=0.828时，方程(1)对应的系统相轨迹图。

由图1可见，γd= 0.827为系统的混沌临界阈值。

2.1噪声对混沌系统的影响

图2给出了纯噪声下的测试结果，图2(a)和(b)为功率为0.1的高斯随机白噪声输入处于临界状态的混沌系统后产生的相轨迹图。由图2(b)可见，混沌系统并不是对噪声绝对免疫，也有一定的概率使系统进入到大尺度周期状态，从而使混沌信号检测方法失效。

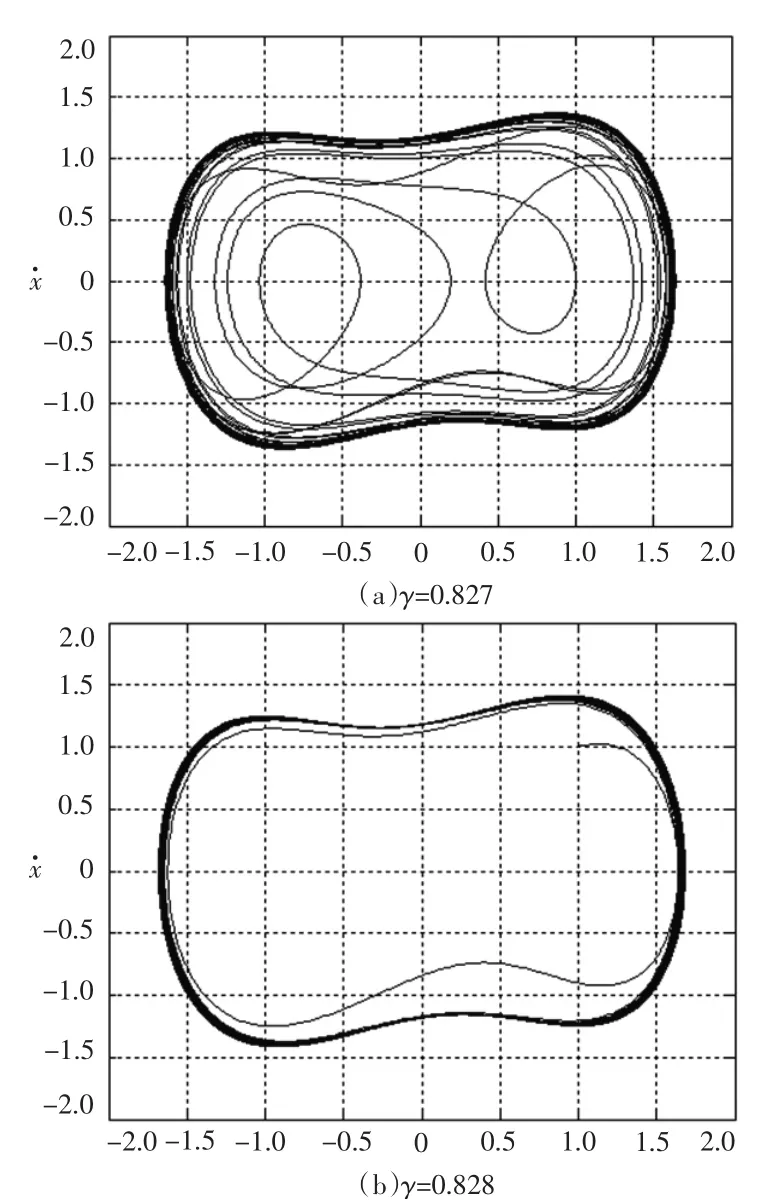
图1　不同γ值下的系统相轨迹图Fig.1　The system phase contrail under different γ

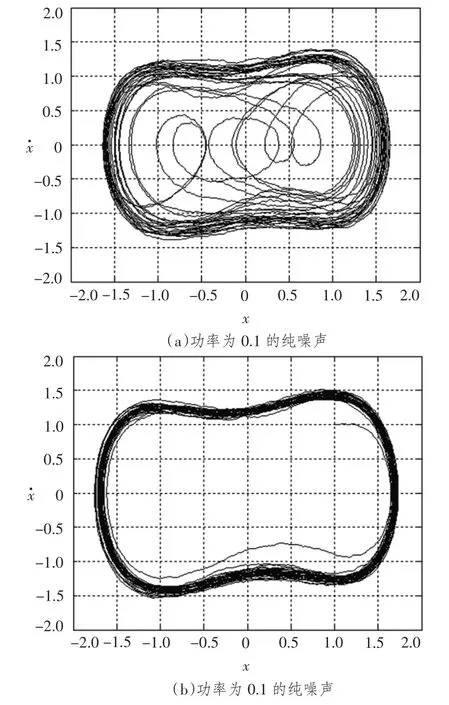
图2　输入功率为0.1的随机纯噪声后的系统相轨迹图Fig.2　The system phase contrail after input random noise with power is 0.1

2.2信号初相位对混沌系统的影响

当输入信号时，混沌系统的方程变为:

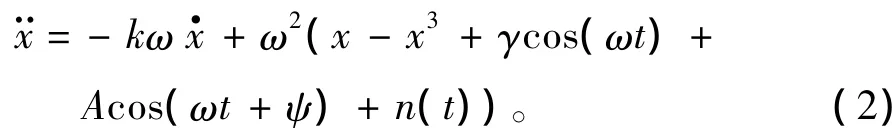
式中: A和ψ分别为输入信号的幅度和初相位; n (t)为随机噪声。

当式(2)中的γ=γd时，输入与内置信号频率相同的信号，其幅度为A = 0.05，白噪声功率为0.5。图3给出了输入含噪信号后的系统相轨迹图，其中(a)和(b)分别对应初相位ψ=0和ψ=π。

图3　输入含噪信号后的系统相轨迹图Fig.3　The system phase contrail after input signal with random noise

由图3可见，信号的初相位对混沌系统检测结果有影响，输入与内置信号频率相同而初相位不同的信号可能不能引起系统的相变，从而使检测方法失效。

3　改进混沌系统基本原理

为避免噪声对混沌系统的影响，可以设置系统的状态远离由混沌向大尺度转化的敏感临界状态，即将方程(2)中的γ值取为小于混沌临界阈值γd，如取γ=0.81，可避免输入纯噪声引起系统的相变。在此情况下，式(2)中，输入信号后，其内置信号变为

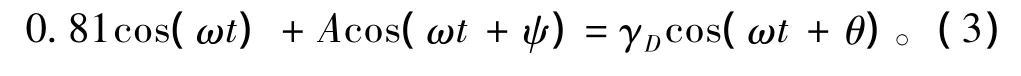
其中

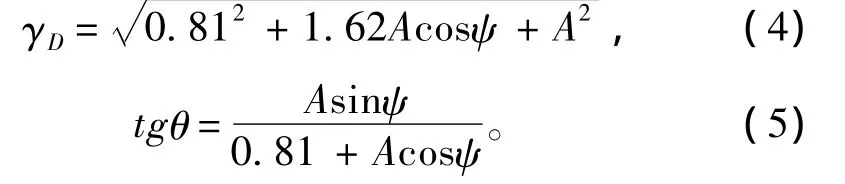
因为是微弱信号，其幅度A＜＜0.81，θ≈0。θ对系统动力学的影响可以忽略不计。

理论上当γD＞γd时，系统就可以发生从混沌向大尺度周期状态的变化，从而将待测信号检测出来。即当满足:

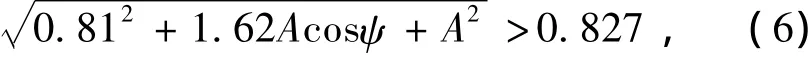
时，系统发生相变。

若已知幅度A，则可以通过式(6)计算ψ的取值范围。设A = 0.035，则通过式(6 )得－62.0172°＜ψ＜62.0172°。仿真分析也表明，当ψ满足该条件时，系统从混沌态向大尺度周期态转换。为了精确检测，放宽信号的初相位为－60°≤ψ≤60°。由式(6)易知，当A＞0.035时，ψ的取值范围将增大。因此当A≥0.035时，满足－60°≤ψ≤60°的输入信号将使系统发生相变，从而可以将该类信号检测出来。对于其他的ψ值，在此条件下将不能引起系统的相变。若将式(2)中输入信号前的“+”改为“－”号，即混沌系统的方程变为:

则内置信号变为

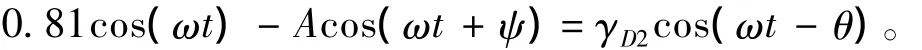
理论上当γD2＞γd时，系统就可以发生从混沌向大尺度周期状态的变化，从而将待测信号检测出来。即当信号初相位满足－180°≤ψ＜－117.9828° 或117.9828°＜ψ≤180°时的信号可以由式(7)的混沌系统检测出来。放宽为－180°≤ψ≤－120°或

120°≤ψ≤180°。

通过式(2)和式(7)的2种混沌系统形式，可以检测初相位为ψ∈［－π/3，π/3］∪［－π，－2π/3］∪［2π/3，π］的信号。对于不在此范围内的初相位，可通过引入内置信号的相位进行补偿来达到检测的目的。将式(2)扩展为如下2类形式:

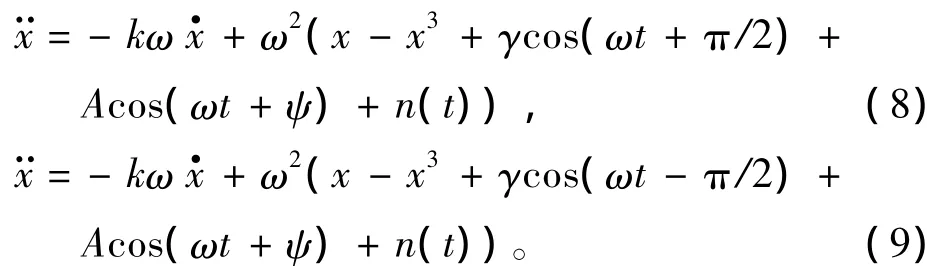
则式(8)检测的初相位范围为ψ－π/2∈［－π/3，π/3］，即ψ∈［π/6，5π/6］，而式(9)可检测的初相位范围为ψ∈［－5π/6，－π/6］。

综合式(2)、式(7)～式(9)的检测范围可覆盖初相位为［－π，π］的整个区间。

因此该改进混沌弱信号检测方法的基本原理是:首先令内置信号的幅度小于混沌临界阈值，如γ= 0.81，然后将待测信号分别输入到混沌方程(2)、(7)～(9)中，若任一方程对应的相轨迹进入大尺度周期状态，则判定待测信号中含有与内置信号频率相同的微弱正弦信号。

4　仿真信号分析

设式(1)中内置信号频率ω=20，当系统初始值为［x，x·］=［1，1］时，其混沌临界阈值仍为0.827，取内置信号幅度γ= 0.81，则当输入纯白噪声时，无论其功率为多少均不能引起系统的相变。当输入信号为0.05cos(20t + 100°) + n(t)时(其中n(t)为功率为0.1的高斯白噪声)，式(2)、式(7)～式(9)对应的系统相轨迹分别如图4的(a)～(d)所示。

由图4可见，当满足一定幅度条件(如信号幅度A≥0.035)的待测信号初相位不为0时，输入到混沌方程(2)中，即使信号频率与内置信号频率相同也不能引起系统的相变，如图4(a)所示。只有将方程(2)扩展为式(2)、式(7)～式(9) 4种混沌方程后，综合4种方程对应的系统相轨迹图才能发现系统状态的变化，如图4(c)所示。图4(b)和(d)对应另外2种不能引起系统相变的情形。

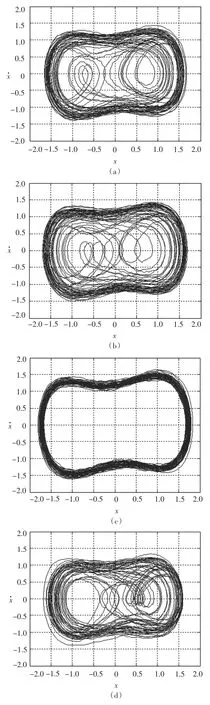
图4　待测信号输入后，方程(2)、(7)～(9)对应的系统相轨迹图Fig.4　The system phase contrail corresponding to equation (2)，(7)～(9) after input detection signal

5　结语

本文针对噪声和待测信号初相位对混沌微弱信号检测结果的影响，提出了改进的混沌系统微弱信号检测方法。该方法将混沌系统内置信号的幅度取为小于混沌临界阈值，可以避免纯噪声引起的系统相变，将常规的混沌检测方程扩展为4种不同的形式，可检测满足一定幅度要求的任意初相位信号。数字仿真结果表明了该改进方法的有效性，下一步将研究该方法的工程实际应用。

参考文献:

［1］楼天良．基于混沌理论的微弱线谱信号检测研究［J］．舰船科学技术，2009，31(1) :96－99．LOU Tian-liang．Research on the detection of weak linearspectrum signals based on chaotic theory［J］．Ship Science and Technology，2009，31(1) :96－99．

［2］周胜，林春生．微弱舰船声信号的混沌处理方法［J］．武汉理工大学学报(交通科学与工程版)，2009，33(1) : 161－164．ZHOU Sheng，LIN Chun-sheng．Application of chaos theory for weak signal of ship detecting［J］．Journal of Wuhan University of Technology (Transportation Science＆Engineering)，2009，33(1) :161－164．

［3］李义方，陈艳峰．基于混沌振子的微弱生命周期信号频率检测方法［J］．计算机工程与科学，2011，33(5) : 183 －189．LI Yi-fang，CHEN Yan-feng．A method of weak vital periodic signals' frequency detection based on the chaotic oscillator［J］．Computer Engineering＆Science，2011，33 (5) :183－189．

［4］陈军．基于混沌理论的检测系统应用研究综述［J］．甘肃高师学报，2013，18(2) :21－25．CHEN Jun．Application research and discussing of detective systems based on chaos theory［J］．Journal of Gansu Gaoshi，2013，18(2) :21－25．

［5］郭玉秀，倪晓红，王玉田．基于混沌弱信号检测的轧机故障诊断研究［J］．工程设计学报，2011，18(3) : 218－221，232．GUO Yu-xiu，NI Xiao-hong，WANG Yu-tian．Study on the fault diagnosis of rolling mills based on the chaos weak signal detection method［J］．Journal of Engineering Design，2011，18(3) :218－221，232．

［6］朱来普，张陆勇，谢文风，等．基于Duffing混沌振子的微弱信号检测研究［J］．无线电工程，2012，42(1) :17－20．ZHU Lai-pu，ZHANG Lu-yong，XIE Wen-feng，et al．Research of weak signal detection based on doffing chaotic oscillator［J］．Radio Engineering，2012，42(1) :17－20．

［7］任志玲，刘银报，史旭鹏．基于Duffing振子的弱正弦信号检测的改进［J］．计算机测量与控制，2011，19(6) : 1301－1303．REN Zhi-ling，LIU Yin-bao，SHI Xu-peng．Improvement of weak sinusoidal signal detecting based on doffing oscillator ［J］．Computer Measurement＆Control，2011，19 (6) : 1301－1303．

［8］李琳，刘春刚，石硕，等．基于混沌和Lyapunov指数的微弱信号检测方法［J］．黑龙江大学自然科学学报，2012，29(4) :556－560．LI Lin，LIU Chun-gang，SHI Shuo，et al．A method of weak signal detection based on chaotic oscillator and Lyapunov exponent［J］．Journal of Natural Science of Heilongjiang University，2012，29(4) :556－560．

［9］赖志慧，冷永刚，孙建桥，等．基于Duffing振子的变尺度微弱特征信号检测方法研究［J］．物理学报，2012，61 (5) :050503．LAI Zhi-hui，LENG Yong-gang，SUN Jian-qiao，et al．Weak characteristic signal detection based on scale transformation of doffing oscillator［J］．Acta Phys．Sin，2012，61 (5) :050503．

［10］陈伟根，张嵩，杜林，等．基于互相关与混沌检测相结合的光声信号检测方法［J］．电力自动化设备，2008，28 (3) :22－26．CHEN Wei-gen，ZHANG Song，DU Lin，et al．Photoacoustic Signal measuring based on cross-correlation analysis and chaotic detection［J］．Electric Power Automation Equipment，2008，28(3) :22－26．

［11］冉莉，王民．一种强噪声背景下微弱信号检测方法研究［J］．信息技术，2012(2) :41－45．RAN Li，WANG Min．Research on weak signal detection method under the strong noise background［J］．Information Technology，2012(2) :41－45．

作者简介:石敏(1979－)女，博士，工程师，主要从事水声信号处理方面研究。

基金项目:国家自然科学基金资助项目(61271418)

收稿日期:2014－10－08;修回日期: 2014－11－18

文章编号:1672－7649(2015) 07－0078－05doi:10.3404/j.issn.1672－7649.2015.07.018

中图分类号:TP391

文献标识码:A