高速小目标回波信号仿真研究
2015-02-21张宝华海军装备部北京100841
张宝华(海军装备部,北京,100841)
高速小目标回波信号仿真研究
张宝华
(海军装备部,北京,100841)
摘要提出基于回波叠加的数值仿真模型,用于目标回波信号的仿真;根据仿真条件,结合多普勒频移公式建立目标回波的理论模型,计算回波信号的频率参数;将目标回波的数值模型和理论模型进行比较,验证了数值模型的有效性,并由此获得高速小目标的回波特性,为进一步的目标回波检测奠定基础。
关键词高速小目标;回波信号;回波检测;仿真
水下高速小目标检测是目前水声学研究中的热点课题,然而利用长脉冲测量高速小目标时由于反射点尺寸小且移动速度快、反射时间短,存在波形不能完整反射、回波相位不连续等问题,一直是水声检测的难点。
声呐是水下测量和监视水下目标的主要工具,以工作方式可分为主动声呐与被动声呐。前者会因为信道复杂和背景干扰严重[1]导致检测精度下降。因此提高主动声呐的抗干扰能力与检测精度成为现代水声学研究的重要课题[2]。
当利用主动声呐探测高速小目标时,存在更加复杂的情况:反射点尺寸小且移动速度快,反射能力弱.[1]。传统的主动声呐检测,常用短脉冲作为发射信号,但是短脉冲的抗混响能力较弱。原因在于高速小目标的速度可达50~60 kn(约25~30 m/s),而此时主动声呐的发射信号频率达几万赫兹以上,因此回波信号较发射信号有很大的多普勒频偏。在对水下高速小目标进行检测时,工作区域主要在近场[3],混响对目标检测的影响较大。为提高回波的抗混响能力,需根据混响和发射信号的强相关性,利用频域差异来区分回波与混响。短脉冲的频率分辨率低,无法在频域将混响与回波信号分离,抗混响能力较弱,而长脉冲则具备较高的频率分辨率,能很好克服这一困难。但在利用长脉冲对高速小目标进行检测时,又存在波形不能完整反射、回波相位不连续等问题。
本文在分析高速小目标运动特性的基础上,建立一种长脉冲高速小目标检测模型,由此对高速小目标的回波波形进行仿真并分析目标回波特性。
1 主动声呐测速原理
当目标相对观察者运动时,观察者接收的信号频率与发射信号的频率不同,产生的频率变化称为多普勒频移。接收信号的频率可由下式计算:

其中,v0是观察者与目标的相对速度,取正值用于相向运动,负值适用于相离运动,c是声速,f0是发射信号频率。主动声呐的测速即是依据多普勒效应,其原理如图1所示,其中水平方向为x轴,目标以速度vx沿x轴方向运动,主动声呐发射波形与目标运动方向的夹角为α。

图1 主动声呐测速原理
由于目标与声源存在径向运动,则照射至目标的波形所产生的多普勒频移为

其中v是目标径向速度,v′是主动声呐的运动速度。图中v= vx⋅cos α,假设v′=0,且v相向运动时取正值,相离运动为负值,则

可以得出速度

主动声呐测速要比一般的多普勒测速多一个回波反射的过程:在波形发射时,目标作为接收者以速度v运动;而在反射过程中,主动声呐是接收者,高速小目标在移动。因此带来了双向的频率偏移,使接收信号的回波频率为

式(5)即为主动声呐回波信号频率与发射信号频率的关系,以此可作为测量目标速度的理论依据。
2 长脉冲检测高速小目标的数值模型
用主动声呐探测水下高速航行的小目标,主要难点在于目标尺度小而背景干扰强。目标尺度小,不仅使其反射本领小,而且要求声呐采用较高的工作频率,这同时限制了探测的作用距离;而干扰背景则主要包括界面混响和回波的起伏等。
因为长脉冲对速度的敏感性高,在高多普勒频移下有很好的抗混响特性,且对噪声的抑制作用也很明显,所以适合用来测量水下高速运动的目标。用于测量高速小目标的主动声呐工作频率一般在几万赫兹以上,波长较短;而高速运动的小目标,尺寸较小,速度达到几十节。因此在使用长脉冲测量高速小目标时,会存在以下几方面的困难:如图2所示,目标尺寸小,运动速度快,因此在脉冲持续时间内,目标已经运动较远距离,使得某一方向上的波形不能被完全反射;由于目标运动速度快,下一个反射点与前一个点的反射角相比有较大变化,可能会造成信道的不一致,使波形相位产生突变,给检测造成困难。
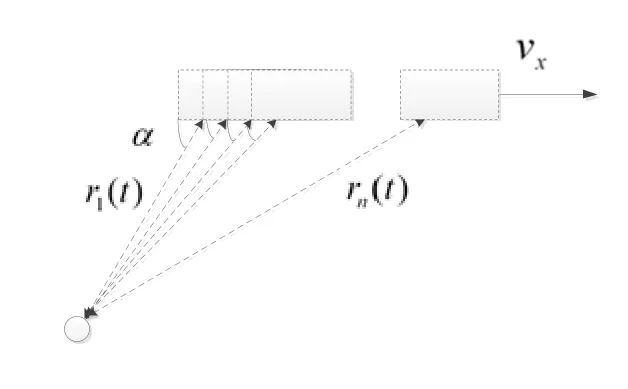
图2 高速小目标回波数值仿真模型
针对长脉冲检测高速小目标的困难,本文提出一种高速小目标回波仿真模型,考虑如下建模方法:将运动目标的轨迹看作无限多细分的离散点,每个点对应高速小目标在运动过程中的一个反射点[4];假设每个离散点在所划分的时间间隔Ti内静止不动,如图2。计算每个离散点的反射回波,设为ri(t),将各个离散点的回波进行叠加,即可获得完整的接收波形[5,6]:
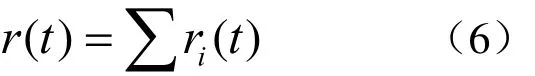
其中每一个离散点的回波ri(t)是目标在Ti内所接触的入射波形si(t)经时延Δτ=di/ c 所得到的波形,即
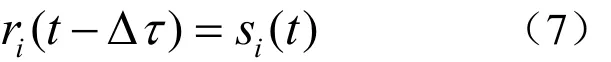
且si(t)与发射信号形式、目标与声源的相对位置、目标的运动状态等有关,在仿真模型中根据具体的参数设置进行计算。
对于叠加后的波形,可以进行频谱分析、匹配滤波等处理,研究目标回波的频域特性,并由此探讨相应的检测方法,估计目标的运动速度等信息。
高速小目标回波的数值模型仿真参数如下:采用频率为10 kHz、时长为0.15 s的CW脉冲作为发射信号,采样频率fs=200 kHz。如图3,在直角坐标系中,以声呐位置为坐标原点,目标起始位置为(30 m,40 m),以30 m/s的速度沿x轴方向运动。为提高目标回波的仿真精度,需使相邻两个反射点之间的时间间隔尽量小。数字信号受采样频率限制,最小的时间分辨力为1/fs,所以设置目标相邻反射点之间的时间间隔为1/ fs。选取第一个波形的反射时间作为时间起点,即只计算单程时延,将0.15 s时间内所有反射点的回波进行叠加,并进行中值滤波,结果如图4所示。

图3 数值仿真坐标图
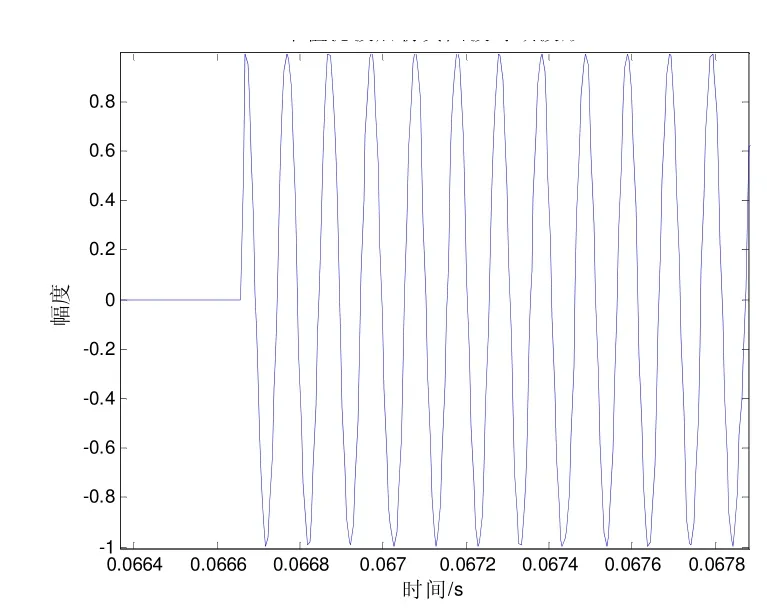
图4 中值滤波后的波形
对接收信号的频谱进行粗略估计,并进行多普勒频移的粗略验证,即对整个信号直接做FFT(快速傅里叶变换),观测信号的平均频移是否符合多普勒频移规律。由多普勒频移的计算公式,以运动目标的初始点来计算运动角度,则运动目标的径向速度为v=vxcosα=18 m/s,且方向为相离,所以符号取负。带入公式(5),计算接收波形的频率应为9762.8 Hz。对发射和接收信号做FFT,频谱如图5所示。上图是发射波形的频谱,峰值在10 kHz;下图是接收波形的平均频谱,峰值对应9754 Hz。受仿真信号频率分辨率限制,结果存在误差,但基本符合实际情况。
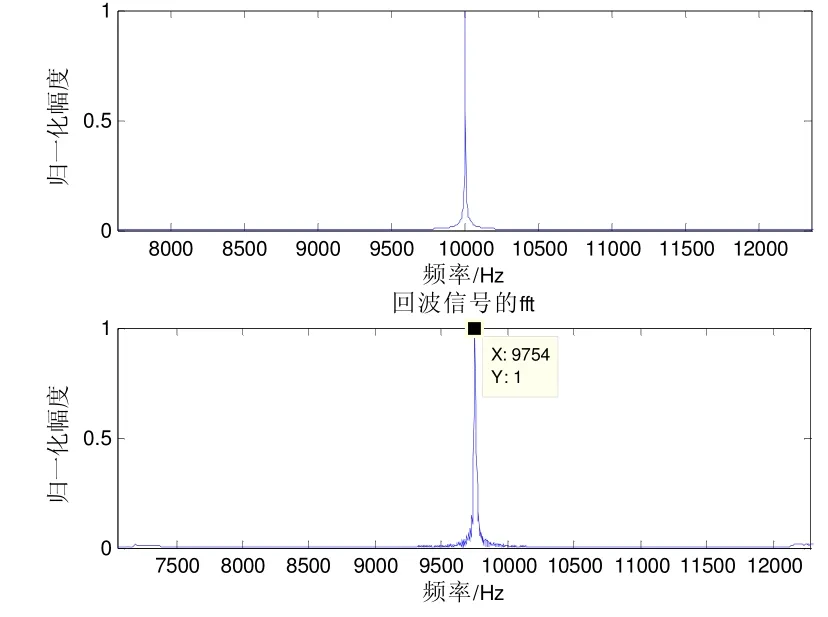
图5 发射信号与回波信号的频谱对比
3 高速小目标回波的多普勒理论模型
设坐标原点为主动声呐,横向为x轴,纵向为y轴。以高速运动的小目标为圆心,运动方向与径向的夹角为α。从零时刻起,运动方向和径向的角度会发生变化,对应的径向速度也会发生变化。高速小目标的运动方向和径向存在一个角度范围:当运动方向和径向平行时,径向速度最大,速度不随时间改变,所以多普勒频移是一个固定值;对应的,在与径向垂直的方向上,径向速度为零值,回波的多普勒频移也是零。因此回波的频率与运动方向相关,可根据理论模型推导出两者的函数关系。

图6 理论模型的几何关系
设目标与坐标原点的初始距离为d0,那么在t时刻,由余弦定理,目标与原点的距离为

t时刻小目标运动方向与径向的夹角记为β,则径向速度为vcosβ,再次利用余弦定理

可得

再根据多普勒频移公式(5)即可得出回波信号频率的瞬时表达式

由此可计算回波信号的瞬时频率,用来验证第2节中数值模型的准确性。此处为了计算方便,未计算传播延时;若要与数值模型进行对比,需要加入反射回程的时间作为时间修正。设发射频率为10 kHz,以(30 m,40 m)为目标的初始位置,对应的α角度为126.87°,计算1.5 s内回波信号的频率随时间变化的规律,如图7所示。

图7 理论计算频率随时间变化
4 数值和理论模型的相互验证
采用第2节中的数值模型对1.5 s发射信号的回波波形进行仿真,如图8(a)所示。为观测波形细节,图8(b)显示了前25 ms的回波波形。用STFT(短时傅里叶变换)精确分析数值模型的结果,即图8(a)中的波形,并与理论模型进行对比。使用窗长为65536点的Hanning窗,逐点移动时间窗,在每个窗内做FFT;搜索每个窗内FFT的最大值点,对应的频率作为每个窗中点位置所对应时间的瞬时频率。时频分析的瞬时频率与时间的关系表示图9,再将数值仿真结果与理论计算结果进行对比。在数值模型的回波分析中,STFT窗长占一定时长,所以频谱图呈以窗长为间隔的阶梯状。尽管如此,数值模型的回波时频曲线与理论模型依然基本吻合。并可以看出,高速小目标的回波信号时频曲线呈非线性特性,这对今后的高速小目标检测中的拷贝信号设计具有指导性。

图8 1.5 s发射信号的回波波形

图9 数值模型仿真与理论模型的对比
5 结论
本文通过运动目标模型分析高速小目标检测存在的困难,并由此建立数值模型,进行目标回波仿真;使用多普勒频移公式建立理论模型,计算回波参数。对数值仿真得到的目标回波波形做频谱分析,并与理论模型进行对比,验证了数值模型的准确性,为今后的高速小目标检测奠定基础。
参考文献:
[1] 杨崇林,姚蓝. 探测高速小目标的声呐信号波形设计[J].声学技术,1999,18(3): 112-115.
[2] 朱埜.主动声呐检测信息原理[M]. 北京: 海洋出版社,1990.
[3] 曹黎明,李耀波. 一种水下高速小目标回波频率估计方法[J]. 指挥控制与仿真,2013,35(5): 106-109.
[4] HAO L,PAKNYS R. Comparison of near-field scattering for finite and infinitie arrays of parallel conducting strips TM incidence[J]. IEEE Transactions on Antennas and Propagations,2005,53(11):3735-3740.
[5] 范军. 复杂目标回波特性预报[D].上海: 上海交通大学,2002:25-52.
[6] 何心怡,蒋兴舟,林建域.基于亮点模型的潜艇回波仿真[J].鱼雷技术,2001,9(3):15-18.
