采用模糊理论的零部件工艺PFMEA评估

盛精， 王君， 罗善明

(厦门理工学院 机械与汽车工程学院, 福建 厦门 361024)

采用模糊理论的零部件工艺PFMEA评估

盛精， 王君， 罗善明

(厦门理工学院 机械与汽车工程学院, 福建 厦门 361024)

为了控制和降低零部件的制造质量风险，在对零部件工艺过程进行分析的基础上，提出基于模糊理论的潜在失效模式及后果分析(PFEMA)方法.通过研究零部件加工过程的风险评估，构建基于生产成本的评价指标；设计评价因素集和因素水平集，并用层次分析法确定评价因素的权重，提出零部件制造工艺的风险评估模型；采用模糊评价决策，定量计算其综合评价值，进而确定其风险等级.以某型号叉车门架系统的横梁加工工艺为例进行实例验证，结果表明：改进后PFMEA方法的可行性和正确性.

工艺过程; 风险评估; 过程失效模式及后果分析; 模糊评价; 层次分析法.

潜在失效模式及后果分析(failure mode and effect analysis，FMEA)是在可靠性工程中取得广泛应用的分析技术.过程失效模式及后果分析(process failure mode and effect analysis，PFMEA)是FMEA中的一部分，通过PFMEA分析，找出工艺过程中威胁生产安全和影响产品质量的所有潜在风险及原因，经采取的风险预防措施，可减少生产过程中的不稳定因素和提高产品的质量[1].Yeh等[2]将模糊评价理论结合FMEA进行系统失效风险分析，改进最初的风险评价方式.Shahin[3]针对失效模式的严重度与发生频率之间非线性的问题，提出采用FMEA与Kano模型相结合的办法，使风险评价的结果更具可比性.高鹏程[4]将FMEA与FTA相结合，使评价的过程更具效率，结果更加准确.陈超[5]提出NFMEA的方法，即结合FMEA与BFA的可靠性建模方法-网状失效分析法，建立失效和系统设计参数之间的关系.聂淼[6]构建了FMEA的数据库系统.然而，这些方法都没有改变传统的FMEA中存在的问题，即它的风险评估的主观性和风险序数(risk priority number,RPN)值的可辨识度不高.因此，本文通过模糊评价的方式，结合基于过程成本制定的PFMEA评判标准，计算出失效模式的危害结论等级值，并以此值取代RPN值作为风险排序的依据.

1 传统PFMEA方法存在的缺陷

1.1 风险判别的主观性与模糊性

传统的PFMEA方法中，确定风险序数RPN的3个参数值(失效严重度S，失效发生频率O，失效探测难度D)都是由定性描述的评价指标结合专家打分得到的.不同的分析团队在同一个失效模式、相同的评价指标下，很可能会得出相差较大的RPN值，从而极大地限制了PFMEA的使用效果.

1.2 风险序数值的分辨度不高

传统的PFMEA中，风险序数RPN的计算公式为RPN=S×O×D.3个重要参数S,O,D的评分范围都是1～10分.令S1=1，O1=6，D1=9，则RPN1=54；令S2=6，O2=3，D2=3，则RPN2=54.可见，2个RPN值完全相等，但2个失效模式的严重度、频度和探测难度都不相同，其风险程度也不相同.同时，3个参数对风险的影响程度不同，在传统的使用RPN值的方法中，也无法体现3个参数各自的权重.因此,传统PFMEA方法得出的RPN值存在分辨度不高的缺陷[7].

2 模糊评价方法建模

2.1 模糊评价的基本方法

运用模糊综合评价方法，将PFMEA中的3个评价因素组成集合U，同时构建由各级评语所组成的评价集合V.进而针对目标中的每一个单个因素ui用V中的评语进行评价，通过选取适当的隶属函数，得到因素集U在评价集V上的隶属度矩阵R，即单因素评价.通过单因素评价，可使传统PFMEA评价方法的主观性和模糊性变得更加客观和接近实际.

通过选用适当的权重分配方法对各评价因素确定权重，最终的PFMEA模糊综合评价模型为

B=W*R.

式中:R为评价因素隶属度矩阵;W为评价因素权重向量;B为评估结果;*为模糊算子.模糊算子的模型主要有主因素决定型，主因素突出型，加权平均型等，根据具体情况的需要进行选择.

由于模糊综合评判的结果B为一个向量，为了使结果更加直观，可将B通过赋值法转化为一个简单的数字，作为评价目标的结论等级值，即

M=B·AT.

式中:A为赋值向量(a1,a2,…,an).通过对各评价因素权重的确定和选择更贴近实际的模糊评判决策，并对模糊综合评价结果的赋值，可使最终得到的风险结果具有更高的分辨度.

模糊综合评价的基本步骤,如图1所示.

图1 模糊综合评价基本步骤

2.2 评价因素集和评价因素水平集的建立

根据模糊数学的基本方法，建立包含所有需要评价的指标的集合[8-9]，即

U={u1,u2,u3,…,ui} .

式(1)中:ui为被评价对象的第i个决定因素.

针对需要被评价的因素，建立水平集合

V={v1,v2,…,vj} .

式(2)中：vj表示评价水平的第j个等级.

2.3 评价因素权重集的确定

在PMFEA中，经常需要将定性分析与定量分析相结合.因此，可用层次分析法确定权重集[10-11].

首先，对评价因素两两进行比较，结合各因素的重要程度得出判断矩阵X=(xi，j)n×n.其中，xi，j取值如表1所示.

表1 判断矩阵取值表

在构造判断矩阵X之后，求出判断矩阵的最大特征值λmax，并用一致性指标和随机一次性指标对其进行一致性检验.

一次性指标为

式中:当C=0时，判断矩阵是一致的；当C的值为负数时，判断矩阵一定是不一致的；此外，C的值越大，判断矩阵的不一致程度越严重.

此时,引入随机一致性指标,即

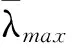
当随机一致性比例C/R<0.1时，判断矩阵的一致性是可以接受的.

当判断矩阵X是一致时，求出其最大特征值所对应的特征向量W，并归一化，得到的向量即是评价因素的权重分配,即

W=(w1,w2,…,wi,…,wn) .

2.4 单因素评价

模糊单因素评价即确定评价因素对评价水平的隶属度.建立模糊映射为

f∶U→Γ(V),

ui→f(ui)={ri,1,ri,2,…,ri,j}∈Γ(V).

模糊映射即隶属函数，可导出模糊关系，即

Rf(ui,vj)=f(ui)(vi)=ri，j.

由于PFMEA的3个评价因素所构成的模糊集，很难直接给出其隶属度.因此,采用二元对比排序法.在确定严重度优先于探测难度，探测难度优先于频度的排序顺序后，采用平均法确定隶属函数,即

ri，j=vi，j/n.

式中:ri,j表示第i项因素ui对第j级评语vj的隶属度；n为参与评价的总人数；vi,j表示第i项因素的第j级评语的评价人数.单因素评价用矩阵表示为

式(4)中：R为单因素评价矩阵，是U到V的模糊线性变换.

2.5 模糊综合评价

将权重集结合单因素评价矩阵，得出模糊评价向量[12],即

式(5)中：*为模糊综合评判决策.在模糊评价中，往往因具体考虑的因素情况不同和评判者偏重点的不同，有多种决策模型可以选择.

在PFMEA评估中，需对所有因素依权重大小均衡兼顾.因此,评判决策中，使用加权平均模型

其结果为一个向量，即

B=(b1,b2,…,bm).

对(b1,b2,…,bm)归一化后，为模糊综合评价向量，代表评价因素的评价等级对v1,v2,…,vm的隶属度分别为b1,b2,…,bm.

2.6 模糊评价结果的处理

根据等级赋值法，构造一个等级赋值向量.将水平集中的评语用能体现水平级别差异的数字代替,即有

A=(a1,a2,…,aj,…,am).

式中：aj为赋予vj水平的数值.这样，利用表达式

可以在模糊评价最终得到一个结论等级值.

3 改进后PFMEA方法的应用

以叉车门架的横梁加工工艺PFMEA为例.L公司是一个叉车专业研发生产企业，该厂为提高产品的质量水平，加强对制造过程可靠性的控制，特引用PFMEA的方法减小过程失效的风险.

将门架横梁的机加工工艺步骤由工艺工程师详细列出，评价组成员需针对失效模式严重度(S)，发生频度(O)和探测难度(D)制定相应的评价指标，并以此对每一道工序逐一进行评价.此项指标一经确定，则在之后对其他型号门架系统的PFMEA评估中，不得轻易更改， 否则， 会造成之前项目中所得的

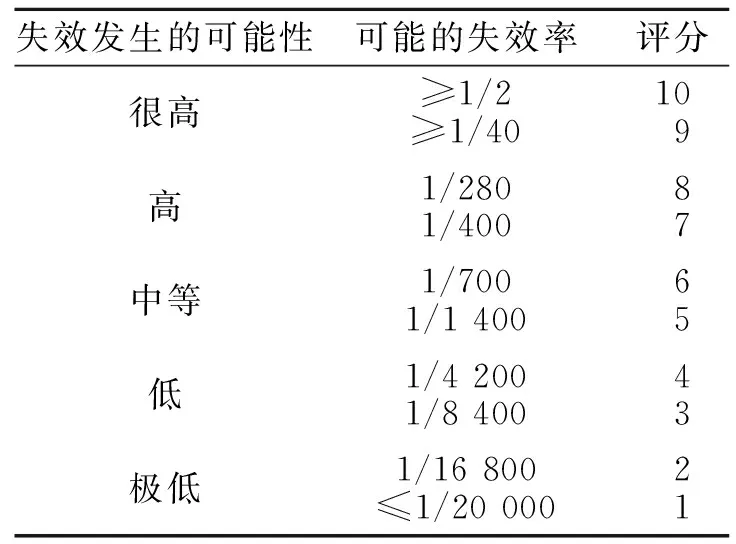
表2 机加工PFMEA频度评价准则

数据与更改标准后所得的数据无可比性.

机加工PFMEA频度评价准则、机加工PFMEA严重度评价准则和PFMEA探测度评价准则，分别如表2～4所示.

该公司根据传统PFMEA方法,得到的加工门架左右板部分工序的风险分析结果,如表5所示.

由表5可知：传统PFMEA分析得出的风险序数RPN值的辨识度不高，不同的过程风险常常出现相同的RPN值，而其严重度、频度和探测难度都不相同.因此，无法区别这种情况下，工序之间的风险大小差异.

将改进后的模糊评判法的PFMEA运用在同样的工序上.以其中RPN值同为45的2个工序为例.

表3 机加工PFMEA严重度评价准则

表4 PFMEA探测度评价准则

表5 传统PFMEA分析

3.1 建立评价因素集和因素水平集

根据PFMEA中的影响风险序数的3个评价指标，建立评价因素集为

U={S,O,D}.

水平集是评价人员对各级评价指标给出的评语集合.根据制定的评价准则，将评价等级分为10级.则得因素水平集为

V={v1,v2,v3,…,v10}.

另外，根据等级赋值法，可构造一个等级赋值矩阵，即

A=(1,2,…,10).

3.2 确定因素权重集

根据层次分析法，建立判断矩阵为

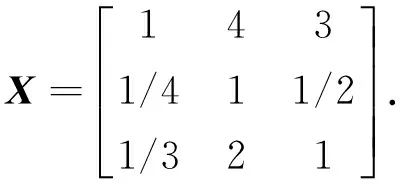
求其最大特征值为3.03.由λmax=3.03,可求得判断矩阵A的一致性指标为0.015，引用撒汀的数据结论，可得随机一致性比例为0.015/0.58=0.026<0.1.因此,判断矩阵A的一致性可以接受，求其最大特征值对应的特征向量，并归一化后，得到评价因素的权重分配为

W=(0.63,0.14,0.24).

3.3 单因素评价

小组中每个成员在不受他人影响的情况下，对每个失效模式的评价因素进行单独打分.根据每个成员(一组有6人)给出的打分，制成统计表,如表6,7所示.

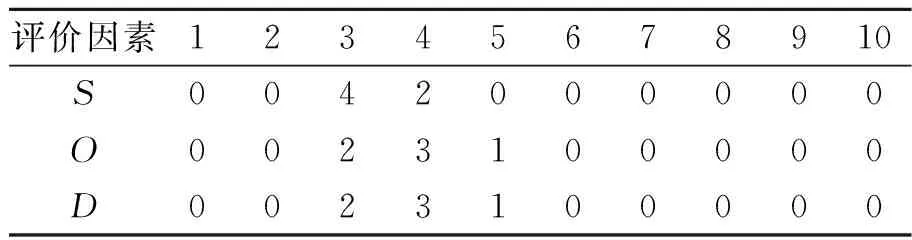
表6 针对失效模式“有锈迹”的评分

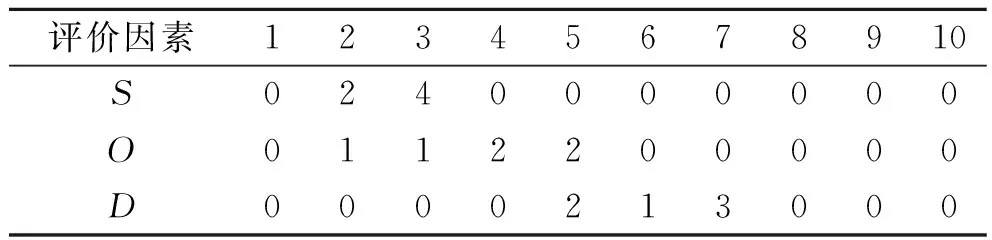
表7 针对失效模式“平面度超差”的评分

由之前确定的隶属函数，可分别确定单因素模糊评价矩阵.其中，失效模式“有锈迹”的模糊评价矩阵R1为

失效模式“平面度超差”的模糊评价矩阵R2为

3.4 模糊综合评价

由式(5)分别计算2个失效模式的模糊评价向量.根据加权平均模型可得

B1=W·R1=(0,0.231 7,0.445 9,0.046 2,0.125 4,0.040 8,0.120 0,0,0,0).

归一化后，得

B1=(0，0，0.542 1，0.394 0，0.063 9，0，0，0，0，0),

B2=(0，0.229 4，0.441 5，0.045 7，0.124 2，0.040 4，0.118 8，0，0，0).

3.5 对模糊评价结果的处理

由式(6),(7)求得模糊评价的最终结论等级值(结果取小数点后两位)为

M1=B1·CT=3.52,

M2=B2·CT=3.66.

由此可知，失效模式“平面度超差”的风险等级比“有锈迹”的风险等级高.证明了传统的PFMEA评价方法是无法区分两者之间风险高低差异的，这样会在大量的相同风险序数下,掩盖了实际上具有高风险的一些工艺过程失效模式;同时,也验证了模糊理论应用于PFMEA评估的可行性和正确性.

4 结论

1) 使用传统PFMEA评价无法体现3个评价因素各自所占的权重，即使得到相同的RPN值，实际上风险程度还是有差异的.使用模糊评价的方法，可以更清晰准确的对工艺过程的风险大小进行排序.

2) 在评价过程中，一个人的主观因素对结果的影响降低了，并且越多的人参与评估，越能得到贴近现实的准确结果.在风险值中,相等的数值越少越利于企业排查生产过程中存在的失效风险.通过结论等级值进行排序之后，绘制帕拉图，可更方便地找出需要重点去改进或关注的工序.

3) 在PFMEA对工艺过程风险进行排序之后，针对预防风险确定改进措施的时候，也可采用模糊评价的方法对提出的改进方案进行优劣的判别和取舍.这样可以使PFMEA在整个执行过程中尽量地减少人的主观因素带来的片面性，得到更准确和更合理的结果.

[1] 中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.系统可靠性分析技术失效模式和影响分析(FMEA)程序：GBT 7826-2012[S].北京：中国标准出版社,2012:5-11.

[2] YEH T M,CHEN Longyi.Fuzzy-based risk priority number in FMEA for semiconductor wafer processes[J].International Journal of Production Research,2014,52(2):539-549.

[3] SHAHIN A.Integration of FMEA and the Kano model: An exploratory examination[J].International Journal of Quality and Reliability Management,2004,21(7):731-746.

[4] 高鹏程.FMEA与FTA在阴极电泳项目质量管理中的应用研究[D].上海：上海交通大学,2011:10-17.

[5] 陈超.基于FMEA和BFA的产品失效分析方法的研究[D].上海：东华大学,2011:12-17.

[6] 聂淼.FMEA技术研究与软件系统发展[D].合肥：合肥工业大学,2007:10-16.

[7] BARENDS D M,OLDENHOF M T,VREDENBREGT M J,et al.Risk analysis of analytical validations by probabilistic modification of FMEA[J].Journal of Pharmaceutical and Biomedical Analysis,2012,64/65(4):82-86.

[8] 赖昱光,管霖,王滔,等.基于模糊综合评判的直流输电系统检修时机选择方法[J].电力自动化设备,2014,34(9):90-94.

[9] 马存宝,李雯,孙焱,等.基于模糊理论的FMEA方法研究[J].测控技术,2013,32(8):137-144.

[10] 李涛.基于模糊层次分析法和灰色关联分析方法的变电站选址研究[D].郑州：郑州大学,2014:15-17.

[11] 崔文彬,吴桂涛,孙培廷，等.基于FMEA和模糊综合评判的船舶安全评估[J].哈尔滨工程大学学报,2007,28(3):263-267.

[12] 梁晓飞,郑小燕,李忠梅.基于可信性理论的桥梁基础施工风险评估[J].合肥工业大学学报(自然科学版),2014,37(12):1483-1487.

(责任编辑： 黄晓楠 英文审校： 杨建红)

PFMEA Evaluation of Parts Process Based on Fuzzy Theory

SHENG Jing, WANG Jun, LUO Shanming

(School of Mechanical and Automotive Engineering, Xiamen University of technology, Xiamen 361024, China)

In order to control and reduce the risk of parts manufacturing quality， based on the analysis of the process of parts and components，the potential failure mode and effect analysis (PFEMA) method based on fuzzy theory is proposed. By studying the risk assessment of parts processing process， the evaluation index based on production cost is constructed. Designing evaluation factor set and factor level set， and the weights of the evaluation factors are determined by the analytic hierarchy process, then risk assessment model of component manufacturing process is put forward. Fuzzy evaluation is used to calculate the comprehensive evaluation value, and then determine the risk level. Taking the cross beam manufacturing process of a certain type of forklift truck door frame system as an example, the results show that the improved PFMEA method is feasible and correct.

process; risk assessment; process failure mode and effect analysis; fuzzy theory; analytic hierarchy process

1000-5013(2015)06-0609-06

10.11830/ISSN.1000-5013.2015.06.0609

2015-07-12

盛精(1965-)，男，教授，博士，主要从事汽车零部件CAD/CAE的研究.E-mail:shengjing@xmut.edu.cn.

国家自然科学基金资助项目(51375411)； 厦门理工学院科研基金资助项目(YKJ11005R)

TH 162.1

A