粒子群与遗传算法的混合算法

阳琼芳, 孙如祥,2

(1. 广西职业技术学院 计算机与电子信息工程系， 广西 南宁 530226;2. 广西大学 计算机与电子信息学院， 广西 南宁 530004)

粒子群与遗传算法的混合算法

阳琼芳1, 孙如祥1,2

(1. 广西职业技术学院 计算机与电子信息工程系， 广西 南宁 530226;2. 广西大学 计算机与电子信息学院， 广西 南宁 530004)

针对粒子群算法直接用于求解离散旅行商优化问题会存在诸多困难，通过分析粒子群算法、遗传算法各自优缺点，将粒子群算法、遗传算法有效结合组成混合算法用于求解离散旅行商问题.混合的目的在于保持两种算法各自的优点，并有效地避免各算法原有的不足.对3个不同规模的巡回旅行商问题进行实验，结果表明：混合算法提升了算法的局部搜索能力.

离散旅行商问题； 遗传算法； 粒子群算法； 自适应； 启发策略.

遗传算法 (genetic algorithm,GA) 起源于Holland教授与其学生对自然界生物进化系统的计算机模拟研究，其本质是一种随机全局搜索的进化算法.它能在搜索过程中自动获取和积累有关搜索空间的特征知识，并自适应的控制搜索过程，最终求得最优可行解.遗传算法的操作以“物竞天择，适者生存”为原则，在可行的解决方案种群中产生一个逐渐逼近最优可行解的方案.1995年,Kennedy,Eberhart 两位博士首先提出粒子群优化算法(particle swarm optimization,PSO)[1-2]，算法源于鸟类寻找食物时的飞行规律.粒子群算法简单明了、收敛迅速而且精度也高，是非线性连续问题的有效求解方法[3].针对遗传算法求解离散旅行商问题(travelling salesman problem，TSP)存在的不足[4-5]，一些学者提出了定位-配给问题(location-allocation problems，LAP)模型[6-8].为了加快粒子群的搜索速度，一些学者采取了自适应的加速因子策略[9-10].为了更好地解决TSP离散问题，需要对粒子群算法的两个位置更新公式进行修改.二元交叉在操作上类似于遗传算法的交叉算子，同时又有粒子群算法学习因子的操作特征.为了进一步加快混合算法的收敛速度，提高算法的收敛精度，采用城市距离远近关系的启发策略.本文通过引入二元交叉操作解决TSP离散问题.

1 混合算法的设计

用路径表示的旅行商问题，若采用基本遗传法中简单的一点或者多点交叉策略，必然产生不能完全遍历所有城市的非法旅行路线.文中采用顺序表示的基因码，配合交叉择优保留策略.即如果交叉之后，个体更加优良，则用子个体替换父代中的较差个体；否则，还原.

1.2 遗传变异算子设计

求解旅行商问题的遗传算法常用的变异算子有常规变异、逆转变异、对换变异、插入变异等.选用对换变异算子，配合变异择优保留策略，对随机的两个码位进行对换，对换后的个体如果得到改进，则保留该次变异，否则，还原.对换变异对采用路径表示的染色体基因的绝对位置影响比较小，也就是说其对码串模式的影响比较小.随着进化的进行，个体的优良基因不断增加，这种变异策略能够在不破坏优良基因的前提下对个体进行改进，而且所需计算也较为简单.

1.3 离散粒子运动方程

近年来，人们提出了多种离散粒子群算法模型，如Wang等[11]提出的基于交换子、交换序两种策略的离散粒子群改进算法.粒子群算法最初是为了解决连续优化的计算问题而提出的，其粒子更新公式是针对连续的对象而设计，因此，需要改造其粒子运动方程才能用于解决离散旅行商问题.离散粒子运动方程[12]改进简化为

X(t+1)=reverse(V(t+1),f,l).

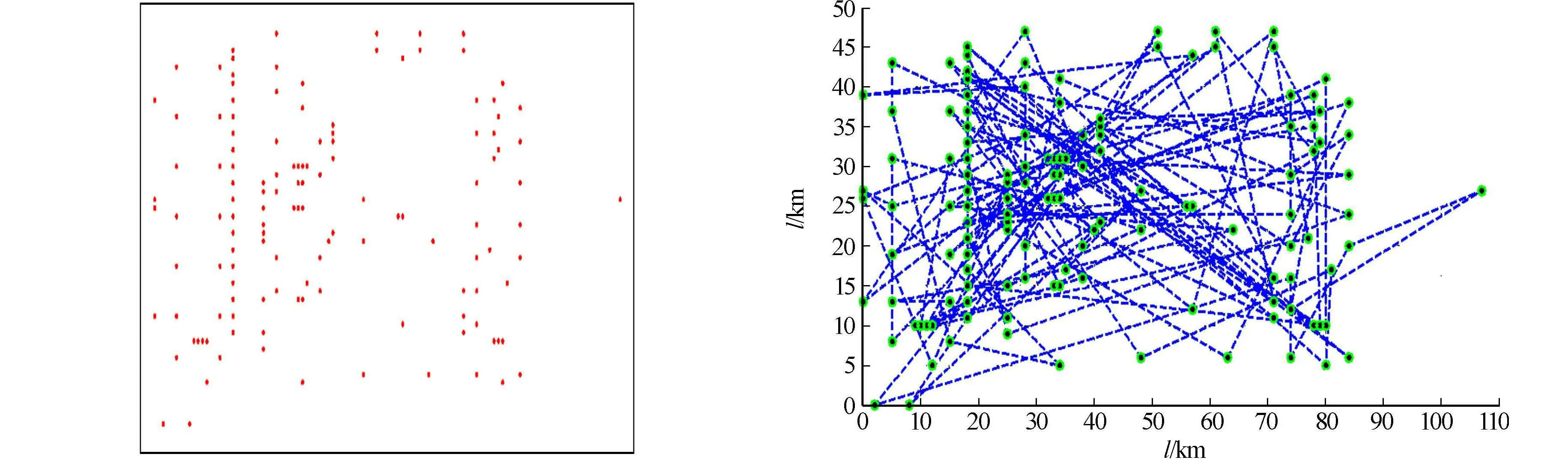
式(1)，(2)中:⊗表示二元交叉运算，类似遗传算法中的交叉思想；x(t)表示t时刻群体中的某个粒子对应的一种旅行路线方案；S(t)表示到t时刻为止，粒子曾经寻找到的最好的旅行路线方案；G(t)表示到t时刻为止，群体中的所有粒子曾经寻找到的最好旅行路线方案；C1和C2对应连续优化计算问题中的两个学习因子；R1和R2为0到1之间符合均匀分布的随机数；C1·R1和C2·R2分别控制当前粒子与个体发现的最佳路线方案和群体发现的最佳路线方案的最大交换长度，离散运动方程通过类似遗传算法的交叉操作实现了对个体最佳可行解和全局最佳可行解的跟踪；reverse(V(t+1),f,l)表示V(t+1)的排列从f的位置开始到l位置结束的子序列进行逆转，其中，f,l为随机整数，并且满足 1≤f≤l

粒子的当前路线方案编码与个体历史最优路线方案编码、全局历史最优路线方案编码的交叉策略通常可以采用遗传算法中的部分匹配交叉或者顺序交叉策略，这两种策略都能保证下一代新个体能够从两个最优个体继承到优良的基因片段，在这些片段中，城市的相对访问次序已经是最佳次序.

这时风歇了，太阳已经西沉。夕阳艳红如血，映出了满天彩霞。姑妈不知所措地划着双手，像一个求救者绝望地挥舞着。夕阳将最后的余晖，洒遍了凌州的每个角落，也洒在了姑妈手上。姑妈的手在夕阳中闪着紫红色的光泽，温馨而耀眼，划出一道美丽的弧。小虫被这道弧吸引了，突然出手抓住，说快快，快摘下钻戒。姑妈也恍然大悟，说对对对，你把钻戒带上，这个钻戒能值二十多万呢，少了不能换呀。小虫说别啰嗦，来不及了。姑妈用力抹钻戒。姑妈手胖，又抖得厉害，怎么也抹不下来。小虫猛地拽过姑妈手指，一用力，钻戒抹下来了。姑妈肥嘟嘟的手指上，被抹出了一道鲜红的血印来。

1.4 启发因子策略

如果没有一些针对TSP问题而设计的特定辅助策略，而只是针对一般的离散优化问题进行一些泛型优化设计，那么，对于规模较大的TSP，在算法演进前期，尽管在寻优速度上可能会有所改进，但在算法的后期搜索阶段，搜索到最优可行解的速度可能会非常缓慢，甚至可能根本搜索不到最优可行解.通过对多个旅行商问题的最终解决方案的研究，发现最佳路径中某个城市的下一个或者前一个访问城市很大程度上都是与该城市距离最近或者相对较近的城市，这个是旅行商问题的最优解的一种特征属性.

启发因子策略在算法开始前需要计算粒子间的相互距离，然后，把结果收集以用于后续的算法搜索[12].当问题规模巨大时，这种计算耗时较长，不适合求解要求快速响应的问题.改进启发因子策略，当粒子进化到一定程度时，而群体中的最优粒子又没有变化时，开始使用启发因子策略.因为在编码位置上，某个城市的最近距离的城市往往就在附近，因此，只需要在某个城市及相邻的几个城市间做小范围调整，即可得到局部最优旅行路线.其具体做法是随机选中一个码位，将它与相邻的或者较近的码位对换，配合择优保留策略，如果得到改良，则保留该次交换；否则，还原.

1.5 混合策略

算法的混合需要遵守一些结合原则[13]，才能有效利用原有进化算法各自的优点，加快收敛速度，保证混合算法求解到的最优可行解的质量高于原有算法，从而达到改进算法的目的.结合粒子群、遗传混合算法的思想，将粒子群算法中每个粒子搜索到的历史最优可行解与遗传算法共享，遗传算子根据指定的进化原则，在这些可行解上进行搜索进化，更新这些历史最优可行解.混合策略既能够保持粒子群算法良好的局部搜索性能，又能够利用遗传算法良好的全局搜索能力.因此，混合策略在粒子群、遗传算法的性能基础上提升了算法性能.

2 实验步骤

混合算法有如下8个主要步骤.

步骤1 设置算法的进化参数：群体规模、终止迭代次数、合理的学习因子C1，C2.

步骤2 初始化粒子群体，并存储记忆当前的最优粒子.

步骤3 开始进化.由于设计的遗传算法保留策略的特殊性，无论是交叉还是变异算子都只会进化到更优的个体.因此，遗传算法的操作对象是粒子群算法中每个粒子曾发现的最优旅行路线染色体编码，粒子群算法操作的是另一个染色体编码，当这个染色体编码代表的旅行方案更优时，才更新覆盖遗传算法操作的染色体编码.

步骤4 执行遗传算法的交叉操作、变异操作，并同时更新存储记忆的历史最优粒子.

步骤5 执行粒子群算法的二元交叉与逆转更新，并同时更新存储记忆的历史最优粒子.

步骤6 判断是否达到使用启发因子策略的条件.如果达到，后续的搜索将一直使用启发策略，执行启发搜索并更新记忆中的最优粒子；否则，继续下一步.

步骤7 如果达到搜索停止条件，则停止搜索；否则，返回步骤4，继续重复执行.

步骤8 算法迭代完成后，种群中的存储记忆的最优结果就是全局最佳旅行路线方案.

3 实验结果与分析

3.1 实验环境

软件编程环境是Microsoft Visual Studio 2010，编程语言是C++，硬件环境是i5-2450 M的处理器、4 GB的内存.选用3个不同的例子进行实验测试，并与文中未结合粒子群算法、未采用启发因子策略但已部分改进的遗传算法(IMGA)的求解结果进行对比，以检验混合算法(IPSOGHA)的有效性.其中，算例1，2来源于文献[14]，其城市规模分别是10个和50个，算例3来源于TSPLIB[15]，其城市规模是131个.3个算例的进化截止代数均为200.

3.2 实验结果对比

算例1的理论最优路径长度为309.642 558，算例2的理论最优路径长度为571.253 118，算例3的理论最优路径长度是567.203 000.IPSOGHA，IMGA算法均能在指定迭代次数内找到算例1的理论最优路径.对于算例2，IPSOGHA算法能在指定迭代次数内找到最优路径，而IMGA算法仅能找到长度为576.168 375的路径.对于算例3，在指定迭代次数内，IMGA算法只能找到长度为587.501 025的旅行路径，而IPSOGHA算法可以找到最优旅行路径.

3.3 XQF131城市进化情况

XQF131的131个城市坐标分布图[15]，如图1所示.初始化生成的路径最优个体，如图2所示.图2中：路程长度(l)为4 103.789 851.经过1次进化，第一代最优个体的路径图，如图3所示.图3中：路程的长度为1 516.901 870.第10代最优个体路径图，如图4所示.图4中：路程的长度为700.517 251.第40代最优个体路径图，如图5所示.图5中：路程的长度为663.286 373.第60代最优个体路径图，如图6所示.图6中：路程的长度为616.076 940.第80代最优个体路径图，如图7所示.图7中：路的程长度为587.501 025.第200代最优个体路径图，如图8所示.图8中：路程的长度为567.203 000.

图1 XQF131的131城市坐标分布图 图2 初始种群最优旅行路线方案

图3 第1代最优旅行路线方案 图4 第10代最优旅行路线方案

图5 第40代最优旅行路线方案 图6 第60代最优旅行路线方案

图7 第80代最优旅行路线方案 图8 第200代最优旅行路线方案

对于10城市旅行商问题，两种算法均能在截止进化代数范围内找到最佳旅行路线，IPSOGHA算法要比IMGA更加优异一些，所需平均进化代数略少于IMGA算法.对于50城市以及131城市旅行商问题，IMGA算法无法在200代之内找到最佳旅行路线，即使将最大截止进化代数增加至300，IMGA算法依旧无法寻找到最佳旅行路线，说明其局部搜索能力不足，无法应对城市数量稍多的旅行商问题.

由图2～8可知：IPSOGHA在算法的执行初期就具有很好的进化能力，初始化生成的最优个体的路程是4 103.789 851，经过仅仅一代的进化便迅速缩短为1 516.901 870；随着进化的不断进行，个体不断接近最优个体.

在后期，算法每10代的进化改进幅度要小于初期的每10代进化幅度，进化速度没有前期那么快.IMGA也具有很好的进化能力，但由于篇幅的限制，没有给出其具体进化路径图.IPSOGHA算法在进化后期虽然速度放缓，但进化仍旧是稳步向前的，IMGA算法则基本停止不前，尽管增加其进化截止次数，但情况依旧很少有改观，其原因在于其局部搜索能力没有IPSOGHA算法好.

3 结束语

对于城市数目少的旅行商问题，未加入粒子群算法及启发因子策略的改进遗传算法同样能在规定的进化次数内快速地找到最优可行方案.但对于城市数目稍微大的旅行商问题，该算法虽然也能寻找到很接近最优的可行方案，但始终不能进化到问题的最优可行路线.对于IPSOGHA算法，尽管在算法进化的后期表现出来的性能没有前期那么优秀，但还是能在较少的进化次数内找到问题的最优解，这样的表现整体上还是不错的，即粒子群算法及启发因子的加入达到了算法结合的目的，提升了算法的局部搜索能力.

[1] 龚纯，王正林.精通Matlab最优化计算[M].北京：电子工业出版社，2009：270-272.

[2] 崔长彩，李兵，张认成.粒子群优化算法[J].华侨大学学报(自然科学版)，2006,27(4):343-346.

[3] 付荣，居鹤华.基于粒子群优化的时间最优机械臂轨迹规划算法[J].信息与控制，2011,40(6):802-808.

[4] 潘文军，王健.基于改进遗传算法的食品召回中心选址研究[J].物流工程与管理，2014,12(36):53-55.

[5] 胡大伟，陈诚.遗传算法和禁忌搜索算法在配送中心选址和路线问题中的应用[J].系统工程理论与实践，2007(9)：172-179.

[6] 付宝英，王启志.自适应粒子群优化BP神经网络的变压器故障诊断[J].华侨大学学报(自然科学版),2013,34(3)：262-267.

[7] 蒋腾旭.改进的遗传蚁群混合算法在TSP中的应用[J].计算机与现代化，2013,12(220):31-33.

[8] 王晓霞，王涛.基于粒子群优化神经网络的变压器故障诊断[J].高电压技术，2008,24(11)：2362-2367.

[9] 詹仕华,王长缨,钟一文.求解TSP问题的伪贪婪离散粒子群优化算法[J].小型微型计算机系统,2011,32(1):181-184.

[10] 赵远东，方正华.带有权重函数学习因子的粒子群算法[J].计算机应用，2013,33(8):2265-2268.

[11] WANG Kangping,HUANG Lan,ZHOU Chunguang.Particle swarm optimization for traveling salesman problem[C]∥Proc of the 2nd International Conference on Machine Learning and Cybernetics Piscataway.Nanjing:IEEE Press,2003:1583-1585.

[12] 钟一文，杨建刚，宁正元.求解TSP问题的离散粒子群优化算法[J].系统工程理论与实践，2006,6(6):89-94.

[13] 江中央，蔡自兴，王勇.求解全局优化问题的混合自适应正交遗传算法[J].软件学报，2010,21(6):1296-1307.

[14] 王秋芬，袁东锋，梁道雷.一种求解TSP的贪心遗传算法[J].制造自动化，2013,35(1):71-74.

[15] Andre Rohe.Forschungsinstitut für Diskrete athematik[DB/OL].[2015-10-05].http://www.math.uwaterloo.ca/tsp/vlsi/index.html#XQF131.

Guangxi Vocational and Technical College， Nanning 530226， China;2. College of Computer and Electronic Information， Guangxi University， Nanning 530004, China)

(责任编辑： 陈志贤 英文审校： 吴逢铁)

Mixed Research on Particle Swarm Optimization and Genetic Algorithm

YANG Qiongfang1, SUN Ruxiang1,2

(1. Department of Computer and Electronic Information Engineering，

There are many difficulties when particle swarm optimization is used directly to solve discrete travelling salesman problem (TSP) optimization problems. Therefore, we analyze the advantages and disadvantages of particle swarm optimization algorithm and genetic algorithm, and then mix them to be an effective algorithm to solve discrete TSP. The purpose of combination is to keep the original advantages of the two kinds of algorithms and to avoid the existing deficiencies. We conduct some experiments on the 3 TSP problems different scales. The result shows that the hybrid algorithm can highly improve the local search ability of algorithm.

genetic algorithm; particle swarm optimization algorithm; self-adaptive; heuristic strategy

1000-5013(2015)06-0645-05

10.11830/ISSN.1000-5013.2015.06.0645

2015-10-08

阳琼芳(1973-)，女，副教授，主要从事农业信息化、计算机应用技术的研究.E-mail:459776040@qq.com.

广西高校科学技术研究项目(2013YB295)

TP 302

A