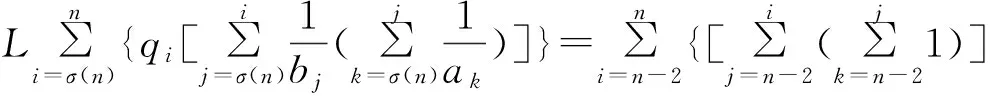三阶非线性差分方程的振动性
2015-02-21王冬梅
王冬梅
(海南大学 信息科学技术学院,海南 海口 570228)
Δ[bnΔ(anΔxn)]+qnf(xσ(n))=0,n≥n0
,
.
,
f(xσ(n))≥Lxσ(n)>0.
Δ[bnΔ(anΔxn)]=-qnf(xσ(n))≤-Lqnxσ(n)≤0,n>n1 ,
Δ(anΔxn) ≥0 .
.
.
xσ(n)>M .
Δ[bnΔ(anΔxn)]≤-LMqn .
,
,
.
,
,
Δ3xn+xn-2=0,n≥3 ,
}=10>1 ,
三阶非线性差分方程的振动性
王冬梅
(海南大学 信息科学技术学院,海南 海口 570228)
利用分析方法研究了三阶非线性差分方程Δ[bnΔ(anΔxn)]+qnf(xσ(n))=0,n≥n0的振动性,并举例说明.
三阶差分方程; 非线性; 振动
近年来,差分方程振动性引起学者们广泛关注,研究成果也很多[2-6].但大部份研究结果集中在二阶差分方程上,三阶的却不多见.文献[1]研究了一类具时滞的三阶非线性泛函微分方程
的振动性,并得到很好的结果.笔者在文献[1]的启发下,考虑三阶非线性时滞差分方程
Δ[bnΔ(anΔxn)]+qnf(xσ(n))=0,n≥n0
(1)
的振动性,其中an>0,bn>0,qn≥0,Δ为向前差分算子,即Δxn=xn+1-xn,Δ3xn=Δ[Δ(Δxn)],函数f(x)满足

(2)
函数σ(n)满足

(3)

定理1 若
(4)
且

(5)
则方程(1)是振动的.
证明 设{xn}是方程(1)的一个非振动解.不失一般性,假设{xn}是方程(1)的一个最终正解,即存在正整数n1>n0,当n>n1时,有xn,xσ(n)>0.
根据条件(2),当n>n1时,有
f(xσ(n))≥Lxσ(n)>0.
(6)
根据式(6),方程(1)转化为
Δ[bnΔ(anΔxn)]=-qnf(xσ(n))≤-Lqnxσ(n)≤0,n>n1,
(7)
即{bnΔ(anΔxn)}是非增的.可以断定:当n>n1时,必有
Δ(anΔxn) ≥0 .
(8)
否则,必存在正整数n2>n1,使得bn2Δ(an2Δxn2)<0.当n>n2由式(7)得bnΔ(anΔxn)≤bn2Δ(an2Δxn2)<0,即

(9)
将式(9)两边从n2到n-1相加得

(10)

(11)
将式(11)两边从n3到n-1求和得
(12)
1)Δxn>0, {anΔxn}是正的非减数列.
存在正整数n4>n1,当n>n4时,有anΔxn≥an4Δxn4>0.即
(13)
将式(13)两边从n4到n-1求和得
(14)
xσ(n)>M .
(15)
由式(7)和(15)得
Δ[bnΔ(anΔxn)]≤-LMqn.
(16)
将式(16)两边从n5到n-1求和得


2)Δxn<0,{anΔxn}是负的非减数列.
当m>n时,将式(7)两边从n到m-1相加得

令m→+∞得
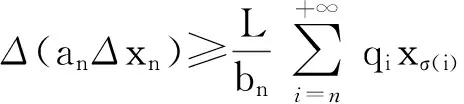
(18)
当r>n时,将式(18)两边从n到r-1相加得
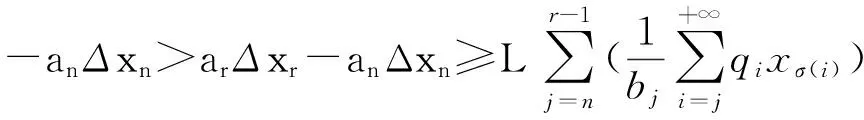
令r→+∞并交换求和顺序得
(19)
当s>n时,将式(19)两边从n到s-1相加得
令s→+∞并交换求和顺序得
将上式中的n用σ(n)替换,再根据σ(n) 即 与式(5)矛盾. 例 考虑三阶时滞差分方程 Δ3xn+xn-2=0,n≥3 , (20) 根据定理1得方程(20)是振动的. [1]CandanT,DahiyaRS.Oscillationofthirdorderfunctionaldifferentialequationswithdelay[J].ElectronicJournalofDifferentialEquations,2003,10:79-88. [2]LiWT.Oscillationtheoremsforsecond-ordernonlineardifferenceequations[J].MathematicalandCompeterModelling,2000,31(6/7):71-79. [3]PadhiS,QianCX.Oscillationofneutraldelaydifferenceequationsofsecondorderwithpositiveandnegativecoefficients[J].MathematicaSlovaca,2009,59 (4): 455-470. [4]KoplatadzeR,PinelasS.Onoscillationofsolutionsofsecond-ordernonlineardifferenceequations[J].JournalofMathematicalSciences,2013,189(5) :784-794. [5]AgarwalRP,WongJY.Oscillationforsecondorderneutraldelaydifferenceequations[J].AdvancedTopicsinDifferenceEquations,1997,404:227-233. [6]ChengJF.Kamenev-typeoscillationcriteriafordelaydifferenceequations[J].ActaMathematicaScientia, 2007, 27B(3): 574-580. Oscillation Criteria of Third-order Nonlinear Difference Equations WangDongmei (CollegeofInformationScienceandTechnology,HainanUniversity,Haikou570228,China) Inthereport,theanalyticalmethodswereusedtoanalyzetheoscillationcriteriaofthird-orderdifferenceequationsΔ[bnΔ(anΔxn)]+qnf(xσ(n))=0,n≥n0.Andanexamplewasusedtoillustratetheresult. third-orderdifferenceequations;nonlinear;oscillation 2015-05-11 海南省教育厅基金(Hjkj2013-09) 王冬梅(1980-),女,山东潍坊人,讲师,硕士,研究方向:微分方程,E-mail:wdm_math@163.com 1004-1729(2015)03-0208-04 O ADOl:10.15886/j.cnki.hdxbzkb.2015.0038