初高中衔接中对二次函数的探究

刘娟丽

（江西省萍乡市上栗中学）

二次函数是初高中重点内容，在新课改下，由于初中有些问题未涉及而影响学习数学的兴趣。下面结合自己多年的教学实践，探究初升高二次函数教材衔接的问题。

一、十字相乘

十字相乘（因式分解）是初中必须掌握的，可速解一元二次方程，还能理解二次函数解析式中的两根式f（x）=a（x-x1）（x-x2）（a≠0）。教学中不能仅局限于二次项系数是1的，如12x2-5x-2，联想到12x2-5xy-2y2进一步联想到如：（x2+x）2-4（x2+x）-12，令t=x2+x，原式=（t-6）（t+2）把二次问题拓展到三次的因式分解，但不宜复杂，如：x3-3x2+2x=x（x-1）（x-2）；又如：巧拆项再分解=x3-3x-2=x3+1-3（x+1）=（x+1）（x+2）（x-1）。

二、一元二次方程

1.数形结合思想。一元二次函数的图象与x轴交点的横坐标就是对应一元二次方程的根,结合函数的图象由判别式Δ符号确定方程根的个数。若Δ＞0，基本都可因式分解确定根，不能因式分解用求根公式；若Δ＜0无根；若Δ=0一根。

2.韦达定理。一元二次方程的根与系数的关系可以用韦达定理中两个式子体现。设，则联想到：

三、二次函数的性质

由于图象直观性，教学中应强调并要求学生会数形结合分析其性质。如：开口，对称轴，顶点，最值，增减性，会写二次函数顶点式。拓展到给定区间求最值问题，如y=x2-3x+1，分别求在-1≤x≤1，1≤x≤2，2≤x≤3上函数最大值、最小值。也可涉及简单的含参数问题。

①a___0；②c___0；③ab___0 ④a+b+c___0

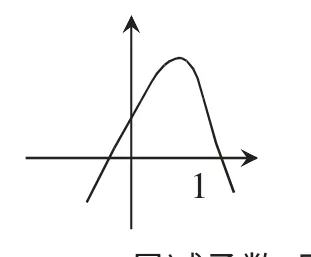
例2.y=x2+bx+1在-3≤x≤3是减函数，则b的范围（ ）.

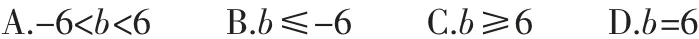
例3.求y=-x2+2ax+1，-1≤x≤1的最大值。

本题注意对称轴x=a，未知a与-1和1的大小关系，故分三种情况讨论。

四、一元二次不等式的解法

（1）确定ax2+bx+c=0（a≠0）的根，但当对于二次方程根不明显的情况下可利用判别式Δ符号画出函数简图解相应不等式。二次函数的图象在x上方满足不等式ax2+bx+c＞0（a≠0）的解，在x下方就满足不等式ax2+bx+c＜0的解。可涉及简单含参的不等式，如：x2-ax≥0，又如：ax2-x≤0；甚至可以联想到简单的含参问题：kx2+x+1＞0对任意的x恒成立，求k的取值范围。这是高中参数不等式恒成立的热点问题。

以上（1）（2）两个内容在高中阶段会强化并熟练掌握。

总之，在二次函数的学习中培养学生利用函数的图象解决一元二次方程，让学生体会数形结合的数学思想。不等式及函数性质的题型及含参数的不等式问题，应分析开口和判别式的符号，让学生感知分类讨论和化归转化的数学思想。