门限CARR模型的实证研究
——以上证市场为例
2015-02-20邹文俊
邹文俊
门限CARR模型的实证研究
——以上证市场为例
邹文俊
(天津大学 管理与经济学部,天津 300072)
金融数据的波动往往存在着非线性的特征,为了更好地刻画上证市场股价指数的波动特征,将门限模型与CARR模型相结合,构建了门限CARR模型。首先借鉴门限自回归条件持续期模型(TACD)的建模方法,构建门限CARR模型;其次选取2002年1月4日至2012年2月15日的上证综合股价指数的日数据进行研究,通过非线性检验和门限值识别的方法找到样本序列的门限值;最后建立了拟合上证股票市场波动的非线性特征的门限CARR模型,得到上证股票市场在高、低波动下的不同波动特征。
非线性;门限模型;CARR模型;波动
针对金融数据的非线性特征的研究是金融时间序列分析中的重要研究领域,对于非线性时间序列模型的研究也逐渐成为学术研究的热点。常见的非线性模型有非线性自回归模型(NLAR)、广义自回归模型(GAR)、双线性模型(BL)、门限自回归模型(TAR)、双门限模型、平滑转移模型(STAR)、向量平滑转移模型(STVAR模型)、人工神经网络模型(ANN)、马尔科夫体制转换模型等。
在以上几种常见的非线性模型中被广泛使用的主要有两种类型,一类是门限模型;另一类是马尔科夫机制转换模型。Hamilton(1989)[1]提出了马尔科夫机制转换模型(Markov regime switching model),此后马尔科夫机制转换模型在时间序列分析上被广泛应用。马尔科夫机制转换模型只能推断出变量在各机制之间的转换概率,而无法描绘出机制转换的非线性形式。门限模型(Threshold models)由Tong(1978)[2]提出,与马尔科夫机制转换模型相比,门限模型以变量本身作为结构转折点,利用类似分段建模的形式采用门限空间来改进线性逼近,能够更加清晰地描述时间序列的机制转换运动状态。
而对于时间序列波动性的刻画,Chou(2005)[3]提出了CARR(Conditional Auto-Regressive Range)模型,即自回归条件极差模型,将极差与GARCH模型的思想结合起来,有效刻画极差的动态结构。使得极差在波动性的预测上,比已被广泛接受的GARCH模型更具有优势。丁忠民等(2005)[4]以上海股市作为研究对象,分别运用CARR模型和GARCH模型进行波动性预测,进而对两种方法的预测能力进行比较,实证结果表明CARR模型在拟合波动性方面优于GARCH模型。程细玉等(2009)[5]以2006年美元对港币5分钟汇率比价和日元对美元15分钟汇率比价的极差和收益率作为样本数据进行实证分析,研究结果表明CARR模型及其衍生模型在高频金融时间序列的价格波动性捕捉方面表现突出。
然而,传统CARR模型和GARCH模型无法很好地拟合存在变结构现象的非线性金融时间序列。对于存在不同波动体制的波动序列还需要引进门限模型的思想。本文将门限模型与CARR模型相结合建模,构建门限CARR模型,选取2002年1月4日至2012年2月15日的上证综合股价指数的日数据进行研究,分别为上证市场股价指数的高波动和低波动建模,刻画上证市场在不同波动体制下的波动特征。
1 门限CARR模型的构建
1.1 CARR模型简介
传统的GARCH模型能够很好地解决金融时间序列中出现的异方差问题,对于金融资产的波动持续性、聚集性和非对称性能够较好地描述, 所以GARCH模型方法在经济金融领域被广泛接受。在此基础上,Chou(2005)[3]提出了CARR(Conditional Auto-Regressive Range)模型,将极差与GARCH模型的思想结合起来,有效刻画极差的动态结构,使得极差在波动性的预测上,比已被广泛接受的GARCH模型更具有优势。GARCH模型通过收益率数据来估计波动性,CARR模型则是通过极差数据来估计波动率,相对于收益率所包含的资产价格变动信息不足的弱点,极差在反映资产价格变动方面占有优势。极差利用了单位交易区间中资产的最高价和最低价两个时间点上的信息,更能反映单位交易区间内的波动情况。
就模型的形式及性质而言,CARR模型类似于GARCH模型,同时也类似于Engle等(1998)[6]所提出的ACD(Autoregressive Conditional Duration)模型。CARR(p,q)模型如下式所示:
Rt=λtεt
(1)
(2)
εt~iidf(·)
(3)
(4)
式中:Rt表示第t期股票价格Vt取自然对数后的极差;λt表示在t期之前的所有信息集合It-1已知的情况下,对第t期极差Rt进行预测的条件期望,λt=E(Rt/It-1),λt≥0;干扰项εt是标准化极差εt=Rt/λt,不同时期的干扰项相互独立,它的分布被假定为服从一个有单位均值的密度函数f(·)的分布;ω表示极差中的不确定性,也可以表示极差的初始水平,ω >0;αi是极差的滞后期系数,可以表示极差条件均值的短期影响,且αi≥0,i=1,2,…,p;βj是极差条件均值的滞后期系数,可以表示极差条件均值的长期影响,且βj≥0,j=1,2,…,q。
Chou提出根据CARR模型干扰项服从不同分布,CARR模型可分为不同种类模型。当干扰项εt服从单位指数分布时,CARR模型的对数似然函数形式为
(5)
干扰项服从上述指数分布的CARR模型称为ECARR模型。
当干扰项εt服从Weibull分布,即εt~Gamma(γ,1/γ)时,CARR模型的对数似然函数形式为:
(6)
干扰项服从上述Weibull分布的CARR模型称为WCARR模型。
1.2 构建门限CARR模型
CARR模型较好地拟合了金融资产的波动性特征,而在现实情况中,金融资产的波动往往会出现不同波动体制的变结构现象,因此构建非线性的CARR模型十分必要。本文构建门限CARR模型的思路借鉴了门限自回归条件持续期模型(TACD)的建模方法。Zhang等(2001)[7]提出了依靠门限变量来描述复杂经济过程的ACD模型,成为TACD模型。首先定义
Rj∈[rj-1,rj),j=1,2,…,J
(7)
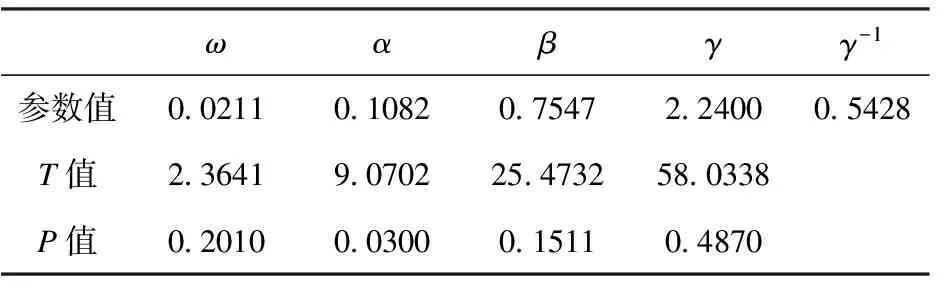
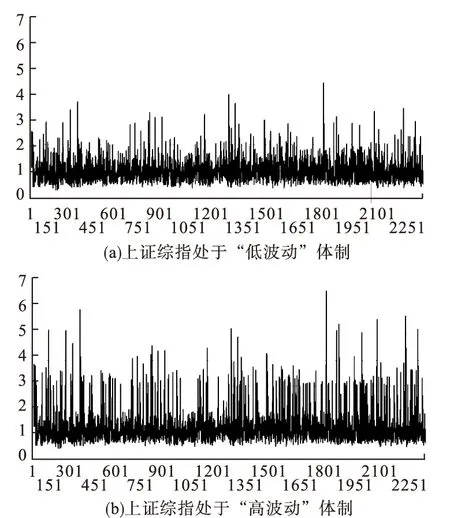
式中:J为正整数;-∞=r0 门限变量定义为 Zi=h(xi,…,x1;yi,…,y1) (8) 式中{yi}为一组与{xi}相关的经济变量。 当Zi-1∈Rj (9) 依据TACD模型的构建方法,本文将构建门限条件自回归极差模型即TCARR模型。将极差作为研究变量,门限变量为极差Rt的一阶滞后项,定义门限空间为Sj,则TCARR模型的基本形式为 (10) (11) 两体制TCARR模型TCARR(2,p,q)可以较好地反映极差波动的非线性特征,同时将金融资产波动分为高波动和低波动两种体制,能够反映出更多的市场微观结构信息。 门限模型是非线性时间序列模型,所以在构建门限模型之前,首先要对样本进行检验,考察其是否具有非线性的特征。金融时间序列的非线性特性检验方法有Hurst指数法、BDS检验法、替代数据法和基于Ljung-Box Q统计量的Mcleod-Li检验法。BDS检验能有效地检测出其他统计检验所忽视的非线性特征,因而在非线性检验中具有很强的功效性,应用较为广泛。本文简要介绍BDS检验方法。 BDS检验是由Brock等(1996)[8]正式提出的。BDS检验运用了关联积分法,零假设为所检验的时间序列是独立同分布的。在进行检验之前,先确定区间大小ε。如果时刻s,t的观察值为ys和yt,则所有的观察值(ys,yt)按对构建为 {(ys,yt),(ys+1,yt+1),…,(ys+m,yt+m)} (12) 式中m为嵌入区间。每对观察值满足ε条件的共有概率被定义为概率cm(ε)。在独立同分布的零假设下共有概率cm(ε)是每对概率c1(ε),c2(ε),…的简化: (13) 如果需要观察的有n个样本,那么就要通过满足ε条件的数对的数量和所有被观察数对来估计: (14)式中Iε为指示函数: (15) 这里的cm,n也可以作为关联积分项来定义。通过关联积分项,BDS检验统计量被定义为 (16) 在零假设为“时间序列yt为独立同分布”时,BDS检验统计值近似于一个标准正态分布:BDS(n,m,ε)→N(0,1) 如果BDS检验统计量是正值,即cm,n(ε)-[c1,n-m+1(ε)]m>0,说明“积聚效应”在价格波动中要比纯粹的随机过程中发生的频率要高。一个正的BDS检验统计量拒绝了残差为独立正态同分布的假设。在实际操作中还应该注意ε和“嵌入区间”m的选择范围。Scheinkman等(1989)[9]指出,当ε取值过小,可能会导致接受零假设;而如果ε过大,那么就会存在对数据过高估计的危险。Hsieh(1989)[10]则建议“嵌入区间”m应该从2到10的区间里选取。m越大,相关函数被高估的风险就越大。文中根据样本个数,m取值为6. 在建立门限CARR(TCARR)模型时,本文选用极差的一阶滞后项Rt-1作为模型的门限变量。接下来就要设定门限值,由于门限值是未知的,需要人为地进行寻找。Chan(1993)[11]提出了一种获得门限值的超一致估计量的方法。本文运用这种方法寻找门限CARR模型的门限值。其估计方法为: 首先,对样本中所有的极差观察值从小到大进行排序,即: R1 对于每个Rj,令τ=Rj,首先将其作为门限值进行门限CARR模型的参数估计。门限值的一致估计量就是该模型的残差最小时所采用的样本值。 而在实际实证分析中,通常不考虑样本中最大的15%和最小的15%的{Rj},使门限的两侧都存在足够多的观察值。将排序后得到的新序列(记其样本共有T′个变量)的第一个值作为门限值带入模型进行门限模型参数的估计,同时需要求出此时的模型的残差平方和,记做resid(1);然后,再将排序后序列中的每个样本值作为门限值进行门限CARR模型的估计,得到残差平方和序列{resid(1)},i=1,2,…,t′。该序列中的最小值resid(k)(k≤t′)所对应的极差序列样本值Rk即为门限CARR模型的门限值。 4.1 数据描述 本文选取2002年1月4日至2012年2月15日的上证综合股价指数的日数据进行研究,经过整理之后总共有2369个极差观察值。本文首先利用上证综合股价指数极差序列所拟合的CARR模型的残差序列进行BDS检验,以判断上证股票市场的极差序列是否具有非线性特征。 表1 上证综合指数的BDS检验 4.2 门限值的设定 由4.1得出上证综合指数的极差序列具有非线性特征的结论,在此基础上,本文建立门限CARR模型。首先要确定门限值。按照前面介绍的门限值识别方法,本文将原极差序列样本进行从小到大的排序,并排除前15%和后15%的样本得到样本容量为1658个的新序列。然后将新序列中的每个样本值一次带入门限CARR(2,1,1)模型中并计算其残差平方和,得到残差平方和序列,见图1. 图1 上证综合指数残差平方和序列 从残差平方和序列分布图并结合样本序列,得出上海综合指数极差序列的第1211个样本拟合的门限CARR(2,1,1)模型的残差平方和最小,得到其模型的门限值为2.744642603。 4.3 建立两体制门限CARR(2,1,1)模型 由4.2得出了拟合上海综合指数极差序列的两体制门限CARR(2,1,1)模型的门限值,将Rt-1作为门限变量,建立拟合上证股票市场波动的非线性特征的门限CARR模型。为了更好地说明门限模型在拟合非线性金融数据中的作用,本文将新构建的两体制CARR(2,1,1)模型与传统CARR(1,1)模型分别拟合样本数据,得到的实证结果如下: 描述上证综合指数极差序列的两体制门限CARR(2,1,1)模型(τ=2.744642603)数据见表2。 表2 两体制门限CARR(2,1,1)模型数据 描述上证综合指数极差序列的CARR(1,1)模型数据见表3. 表3 CARR(1,1)模型拟合数据 表2中,各均值方程各参数值旁的方括号和圆括号内的数据为其参数的T统计量及P值。 在95%的置信水平下,T(40)=1.684,而T(2369) 表3中,ω、β和γ的P值在95%的置信水平下不能推翻参数为零的假设,故参数不显著。 从以上的实验结果可以看出,两体制门限CARR(2,1,1)模型相对于传统CARR(1,1)模型,对于上海股票市场数据拟合程度更好,并且对于上海股票市场在低波动和高波动体制下的波动特征进行了有效地刻画,其对数似然函数值达到了-2924.18841599,较好地体现了上海股票市场波动的非线性特征。 图2为上证综合指数波动在不同体制下的模型的残差项序列 图2 上证综合指数波动处于两种体制下的 从图2中可以明显看出,处于不同体制下的波动序列存在明显差别,在高波动体制下波动特征更加明显,这充分说明了两体制门限CARR(2,1,1)模型可以非常明显地刻画出上证股票市场在不同波动体制下的波动特征。 从上述实证结果可看出,我国上证股票市场存在不同波动体制,这与现实情况十分契合。在现实情况中,由于金融危机,信息不对称,庄家操纵股价,投资者不理性等问题,股市会产生剧烈波动,这时如果仍用单一波动体制来刻画金融时间序列就会刻画不充分。将变结构的非线性模型与传统刻画波动的模型相结合,能够更加准确地刻画剧烈波动的金融市场。 本文将门限模型与CARR模型相结合构建门限CARR模型,利用构建的门限CARR模型对上证市场股价指数的波动进行了研究。在实证研究中,两体制门限CARR(2,1,1)模型很好地描述了上证市场股价指数在高波动和低波动时的不同特征。本文尝试用非线性模型中的门限模型与刻画波动的CARR模型相结合来拟合金融市场数据,在未来的研究中,可以扩展到更加广泛的非线性模型的应用,比如马尔科夫体制转换模型等。 [1] Hamilton J D,Susmel R.Autoregressive conditional heteroskedasticity and changes in regime[J].Journal of Econometrics,1994,(64):307-333. [2]Tong H.On a Threshold Model[M].Pattern Recognition and Signal Processing,Amsterdan:Sijthoff&Noordhoff,1978:101-141. [3]Chou R Y.Forecasting financial volatilities with extreme values:the conditional autoregressive range (CARR) model[J].Journal of Money’ Credit and Banking,2005,37(3):561-582. [4]丁忠明,夏万军.中国股市波动的CARR模型分析[J].商业经济与管理,2005,(12):41-45. [5]程细玉,夏天.金融市场波动性CARR类模型与GARCH类模型的比较研究[J].数学的实践与认识,2009,(13):12-18. [6]Engle R F,Russell J F.Autoregressive Conditional Duration:a New Model for Irregular Spaced Transaction Data[J].Econometrica,1998,66(5):1127-1162. [7]Zhang M Y,Russell J,Tsay R.A nonlinear autoregressive conditonal duration model with applications to financial transactions data[J].Journal of Econometrics,2001,(104):179-207. [8]Brock W A,Dechert W D.LeBaron Scheinkman J.A.A Test for Independence Based on the Correlation Dimension [J].Economic Review,1996,(15):197-235. [9]Scheinkman J A,LeBaron B.Nonlinear Dynamics and Stock Returns [J].The Journal of Business,1989,62 (3):311-337. [10]Hsieh D A.Modeling Heteroscedasticity in Daily Foreign-Exchange Rates[J].Journal of Business & Economic Statistics,1989,7(3):307-317. [11]Chan K S.Consistency and limiting distribution of the least squares estimator of a threshold autoregressive model [J].Ann.Statist ,1993,(21):520-533. (责任编辑:马金发) Empirical Study on the Threshold CARR Model:An Example from Shanghai Stock Market ZOU Wenjun (College of Management and Economics,Tianjin University,Tianjin 300072,China) The volatility of financial data often has nonlinear characteristics.In order to describe the volatility characteristics of Shanghai stock market,we combined the threshold model and CARR (Conditional Auto-Regressive Range) model to construct the threshold CARR model.First,we borrowed the lessons from the threshold autoregressive conditional duration model (TACD) to construct the threshold CARR model;Secondly,we used the daily data of Shanghai stock market from January 4th,2002 to February 15th,2012 as the sample and find the threshold value through the nonlinear test and threshold recognition method;At last,we established the threshold CARR model which fit the nonlinear characteristics of the volatility of Shanghai stock market and describe the different volatility characteristics of Shanghai stock market. nonlinear characteristics;threshold model;CARR model;volatility 2014-09-23 国家自然科学基金资助项目(70901055);国家社会科学基金资助项目(14CTJ012);教育部博士点新教师基金资助项目(20090032120031);天津大学自主创新基金项目 邹文俊(1990—),女,硕士研究生,研究方向:金融时间序列分析. 1003-1251(2015)02-0078-06 F830 A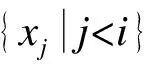
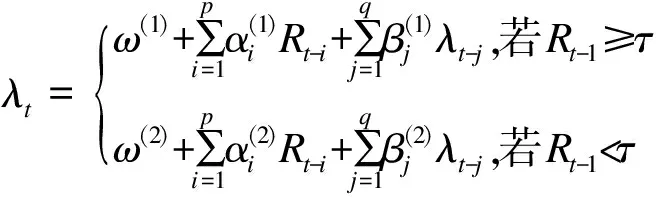
2 非线性检验

3 门限值识别方法
4 实证研究

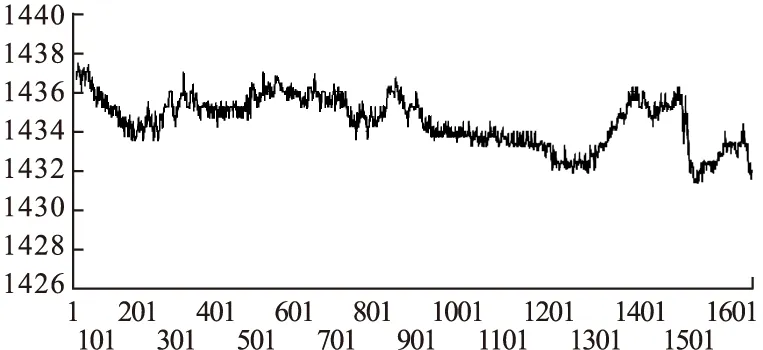
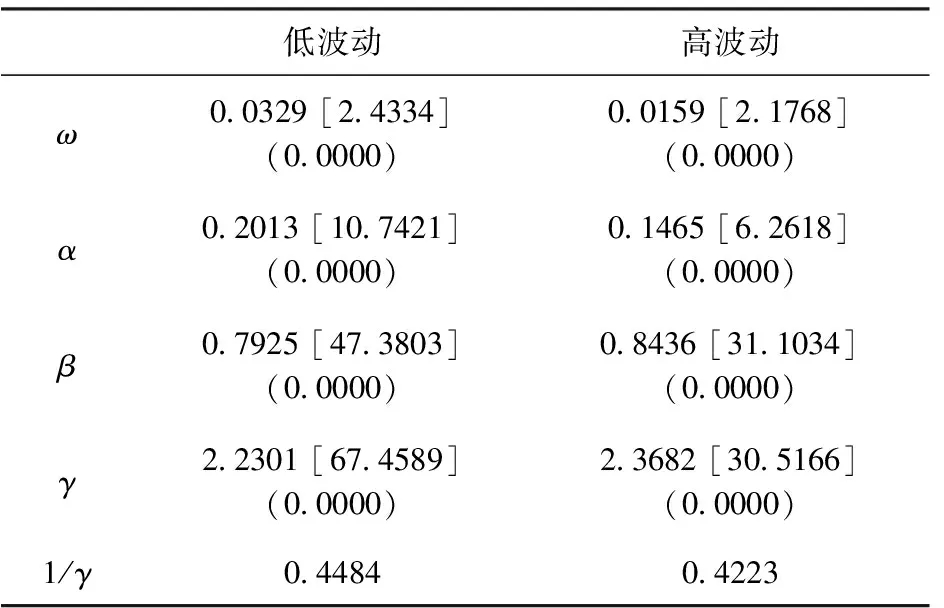
5 结束语
