声发射信号小波阈值消噪方法研究
2015-02-20陈光曦
刘 军,陈光曦
(沈阳理工大学 信息科学与工程学院,辽宁 沈阳 110159)
声发射信号小波阈值消噪方法研究
刘 军,陈光曦
(沈阳理工大学 信息科学与工程学院,辽宁 沈阳 110159)
声发射信号在采集、转换和传输过程中,由于受到设备、环境及传输信道的影响,不可避免地受到噪声干扰。因此,如何去除信号中的噪声,得到感兴趣的信息成为信号处理中一项关键技术。对声发射信号的小波变换阈值消噪方法进行了研究。首先分别对原始信号进行三重db3和sym8小波分解,然后对分解后的各层系数采用硬软阈值方法进行截断处理,最后利用阈值处理后的小波系数完成信号小波重构。通过试验数据分析比较发现,采用sym8小波基的软阈值消噪方法显著提高了声发射信号的局部弱特征保持能力。
小波变换;硬阈值;软阈值,信号消噪
信号消噪是获取信号准确特征的前提条件。经典的傅立叶分析通过构造不同类型的滤波器来实现信号消噪,但是无法有效消除遍布于整个频率范围内的噪声。此外,实际工程测量中获取的信号除含有大量加性噪声外,还包含有大量有用的局部弱特征信息[1],例如桥梁关键结构支承点动态载荷声发射信号,同时含有加性噪声和局部微弱闪变特征。小波消噪在实现低通滤波消噪特性的同时,还能成功保留信号的局部弱特征,因此小波消噪性能明显优于传统低通滤波消噪[2]。小波变换的稀疏性决定了真实信号小波变换的能量集中于有限小波系数,大部分小波系数接近于零,而噪声经小波变换后仍近似为噪声,能量均匀分布于所有小波系数[3]。小波阈值消噪方法通过估计阈值对小波系数进行截断处理,把绝对值小于阈值的系数置为零,而对绝对值较大的系数通过阈值函数映射加以保留或收缩,然后对经过阈值处理后的小波系数进行小波逆变换重构,即可达到消噪目的[4]。
1 小波阈值消噪原理及算法分析
1.1 小波阈值消噪原理
设小波母函数为Ψ(t),将小波母函数进行伸缩和平移,设其伸缩尺度因子为a,a>0,平移尺度因子为b,令其平移和伸缩后的函数为Ψ[(t-b)/a],则有
(1)
式中,Ψ[(t-b)/a]为依赖于参数a、b的小波基函数。对连续信号函数f(t),式(1)称为f(t)的连续小波变换[4],记为ω(a,b)。在实际应用中,当伸缩尺度因子a和平移因子b分别二进取样为k·2-j和2-j时,则连续小波变换(1)转换为离散小波变换:
(2)
式中,ωj,k为二进尺度因子j和平移因子k下的小波系数。利用取样的小波系数ωj,k可以重构连续信号f(t),得到离散小波逆变换重构公式:
(3)
同理,还可以利用离散小波变换将含噪信号f(t)=s(t)+n(t)(其中s(t)为原始信号,n(t)为噪声信号)分解为离散平滑分量Aj(k)和离散细节分量dj(k),而加性噪声对原始信号的干扰作用主要包含在离散细节分量中,因此可以通过对离散细节分量进行阈值消噪来达到对含噪信号f(t)进行消噪处理的目的。
1.2 小波阈值消噪算法分析
小波阈值消噪算法的关键是阈值处理,包括阈值估计和阈值函数的选取。小波系数阈值处理直接决定信号消噪质量。因此,阈值估计和阈值函数选取成为阈值消噪方法的重点和难点。对硬阈值和软阈值消噪算法中阈值处理的设计思想分述如下:
(1)用Mallat塔式分解对含噪信号f(t)进行小波分解,根据式(2)得到f(t)在各尺度下的小波系数ωj,k。
(2)根据小波系数估计门限阈值T,用门限阈值函数对各尺度下的小波系数进行筛选。其中硬阈值门限函数为
(4)
软阈值函数为
(5)
(3)门限阈值估计的经验公式为
(6)
式中:γ为常数取0.1;n为小波系数的个数;门限阈值T依赖于噪声方差σ的估计,用中值估计器估计噪声方差σ:
(7)
对于每层小波分解,由于门限阈值T为常数,因此阈值方法称为固定门限小波消噪。硬阈值和软阈值方法均存在缺陷,如硬阈值函数的不连续性,软阈值函数估计得到的小波系数与信号小波系数之间存在恒定偏差等。
2 阈值消噪算法设计
依据张平等人[5]对声发射信号分析中小波基函数选取问题的研究结果,从Daubechies和Symlets小波基中选择db3和sym8作为小波基对原始声发射信号进行小波消噪处理。小波阈值消噪算法的流程为:
(1)对含噪信号f(t)进行离散小波变换并完成三重小波分解,得到三组小波系数ωj,k;
(2)对小波系数ωj,k分别根据硬阈值和软阈值门限函数进行阈值处理,得到估计小波系数;
(3)利用处理后的小波系数进行小波重构,得到消噪后的信号f′(t)。
3 试验验证
选取桥梁关键结构支撑点动态载荷声发射信号进行消噪试验,信号长度为1450。采用三种阈值消噪方法:强制阈值消噪(小波系数高频部分强制置零)、硬阈值和软阈值,通过试验验证阈值方法的有效性并比较db3和sym8小波消噪性能。分别采用db3和sym8小波对信号进行三重分解并得到小波系数,对三层小波系数d1、d2、d3分别进行上述三种阈值处理,然后分别重构出消噪后的信号,实验结果如图图1~图4所示。
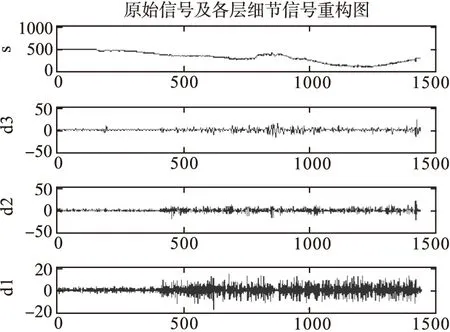
图1 采用db3小波分解
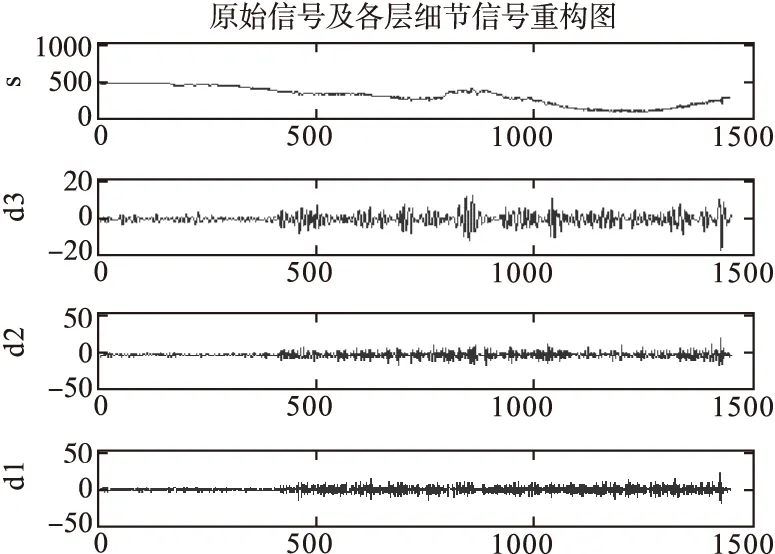
图2 采用sym8小波分解
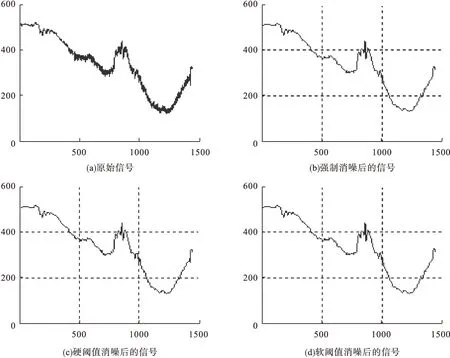
图3 采用db3小波基函数的阈值消噪试验结果
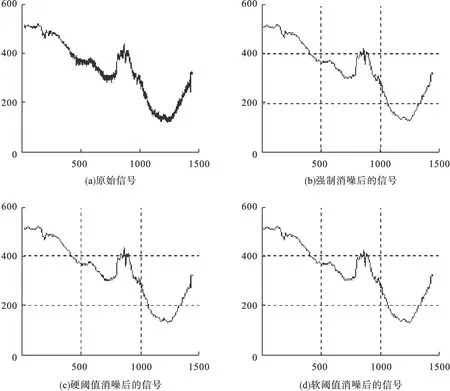
图4 采用sym8小波基函数的阈值消噪试验结果
从图1、图2 可见,db3小波系数的噪声能量主要存在于d1中,而sym8小波系数的噪声能量主要存在于d3中,从图3、4可看出,当采用上述三种阈值方法进行消噪时,虽然消噪效果都很明显,但是sym8小波软阈值消噪方法将保留更多的原始信号细节分量,所以它比db3小波阈值消噪方法具有更强的局部弱特征保持能力。
4 结论
针对桥梁关键结构支撑点动态载荷声发射信号中存在加性噪声的问题,采用硬软阈值方法对声发射信号进行小波消噪处理。对原始信号进行三重db3和sym8小波分解,然后对分解后的各层系数采用硬软阈值方法进行消噪处理,通过试验数据分析比较发现, sym8小波软阈值消噪方法显著提高了声发射信号的局部弱特征保持能力。
[1]耿荣生,沈功田,刘时风.声发射信号处理和分析技术[J].无损检测,2002,24(1):23-28.
[2]唐世伟,林君.小波变换与中值滤波相结合图像去噪方法[J].哈尔滨工业大学学报,2002,24(1):1334-1336.
[3]SHAO Qunfeng,ZHANG Xiaoping,QIA Xiaoqiong,et al.Optical wavelet de-noising applied in multi-span nonlinear fiber links[J].Optics Communications,2010,283(7):1261-1267.
[4]杨建国.小波分析及其工程应用[M].北京:机械工业出版社,2005.
[5]张平.集成化声发射信号处理平台的研究[D].北京:清华大学,2002.
(责任编辑:马金发)
Research on Wavelet Threshold De-noising Methods for Acoustic Emission Signal
LIU Jun,CHEN Guangxi
(Shenyang Ligong University,Shenyang 110159,China)
Acoustic Emission signal is inevitably interfered by noises caused by devices,environment,and transmission channel in the process of acquisition,transform and transmission.Therefore,how to dispose noises from noisy signal to obtain interesting information is one key technology in signal processing.The wavelet threshold de-noising methods have been researched for acoustic emission signal.Firstly the original signal is triple decomposed with db3 and sym8 wavelets.Secondly these decomposed wavelet coefficients in different layers are truncated with hard and soft threshold methods.Finally wavelet reconstruction is accomplished with these threshold processed wavelet coefficients.Through experimental data comparison and analysis,it is found that local weak characteristics preservation ability of acoustic emission signal is significantly improved with sym8 wavelet soft threshold de-noising method.
wavelet transform;hard threshold;soft threshold;signal de-noising
2014-10-28
辽宁省科学事业公益研究基金资助项目(2012004002);辽宁省科学计划资助项目(2012217005)
刘军(1972—),男,副教授,工学博士,研究方向:智能传感器与检测技术,图像与信号处理.
1003-1251(2015)02-0012-04
TP391.4
A
