分数阶系统的自适应PID控制器参数优化
2015-02-20张艳珠王艳梅
张艳珠,葛 筝,王艳梅
(沈阳理工大学 信息科学与工程学院,辽宁 沈阳 110159)
分数阶系统的自适应PID控制器参数优化
张艳珠,葛 筝,王艳梅
(沈阳理工大学 信息科学与工程学院,辽宁 沈阳 110159)
随着分数阶微积分理论的深入研究,越来越多的复杂系统应用分数阶模型表征更加准确,然而将经典控制器方法应用于分数阶系统时,会出现收敛速度慢和超调量大等问题。针对分数阶系统研究分数阶控制器的参数优化问题。以绝对误差积分模型(ITAE)作为性能指标,引入遗传优化算法实现对分数阶PIλDμ控制器的参数优化,该改进算法通过自适应选择交叉概率和变异概率来优化分数阶PIλDμ控制器的多个参数的选择。仿真结果说明,分数阶PIλDμ控制器能够很好地解决分数阶系统应用经典控制器出现的问题,提高了系统的收敛速度,大大改善了系统的控制性能。
分数阶PIλDμ控制器;分数阶系统;参数优化;自适应遗传算法
近年来,分数阶PIλDμ控制器在控制工程领域得到更多的关注。分数阶PIλDμ控制器最先由Podlubny教授提出的,引入了微分阶次μ和积分阶次λ,是整数阶PID控制器概念的推广[1-2]。由于控制器多了两个可调参数,因此,控制参数的整定范围变得更大,能更加灵活地控制被控对象。
目前,众多学者针对经典PID控制器参数进行整定和优化,提出很多方法,如Z-N法、梯度法、Cohen-Coon整定法、单纯形法等。但是在逐步研究的过程中发现这些方法有一定的缺陷,运算量大,容易陷入局部最优点等问题。近年来,随着计算机技术的发展,一些智能算法被广泛引入参数的优化选择中,如粒子群算法、神经网络算法、蚁群算法、遗传算法等等。文献[3]是基于混合PSO神经网络的自整定分数阶PIλDμ控制器的设计,其可适合不同的对象和过程。文献[4]是基于交流电机振动抑制问题,提出基于遗传算法的分数阶PIλDμ控制器的参数整定,改善了交流机的振动抑制特性。
针对经典PID控制器在分数阶系统中存在的问题,本文提出应用分数阶PIλDμ控制器控制分数阶系统,提出一种基于遗传算法的自适应优化分数阶PIλDμ控制算法,遗传算法有很强的寻优搜索能力,根据仿真结果得出,该算法在保证了收敛性的同时,明显降低了系统的超调量,证明了算法的有效性。
1 分数阶微积分及分数阶PIλDμ控制器
分数阶微积分是整数阶微积分在阶次上向任意阶次的扩展的一个推广的整数阶的微积分。根据分数阶微积分理论的基础,发展得出了多种不同的分数阶微积分的定义[5],比较常用的有以下两种:
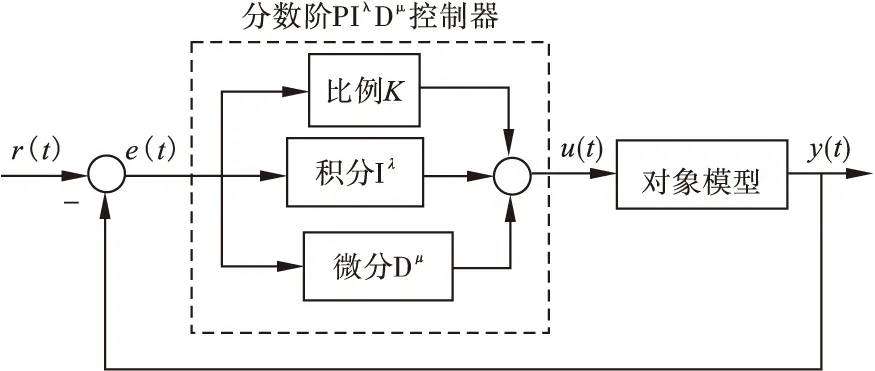
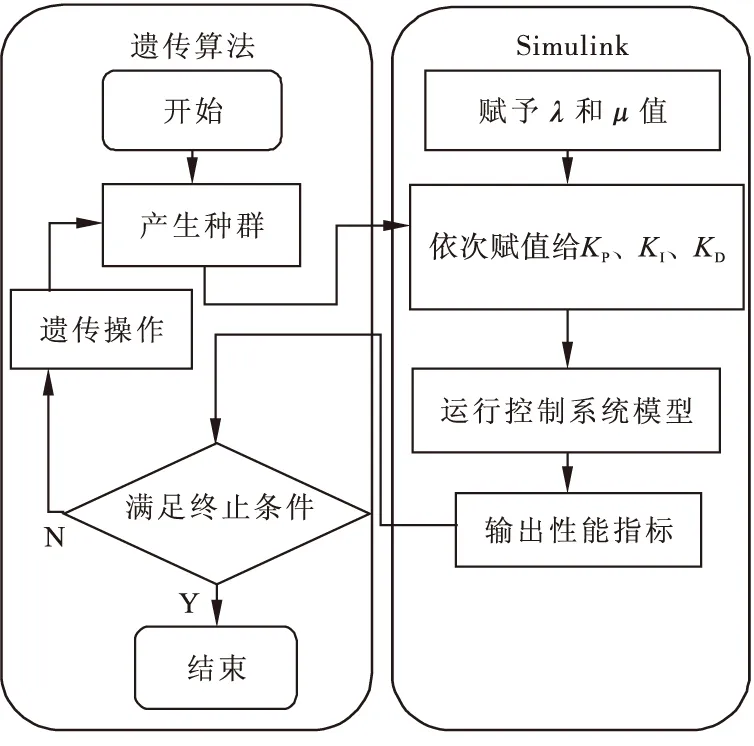
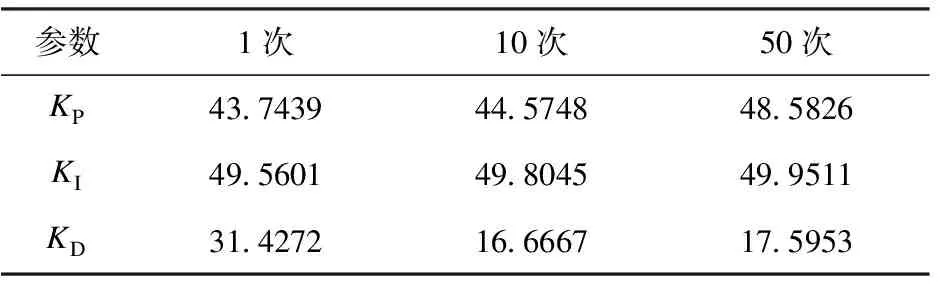
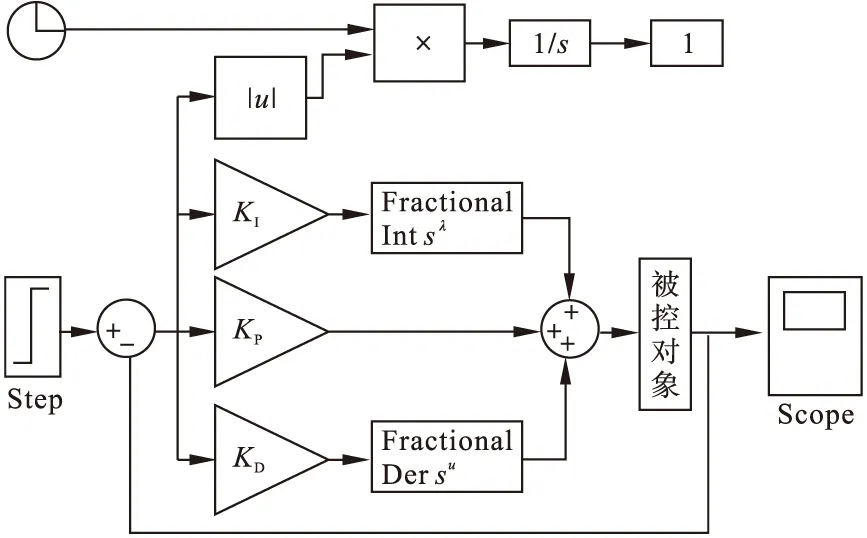
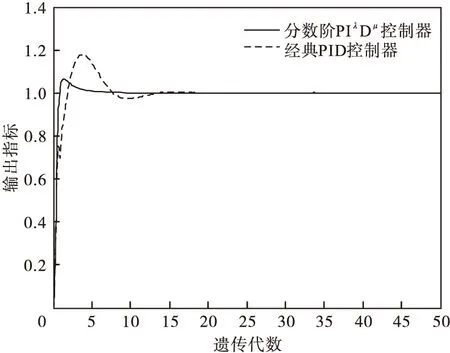
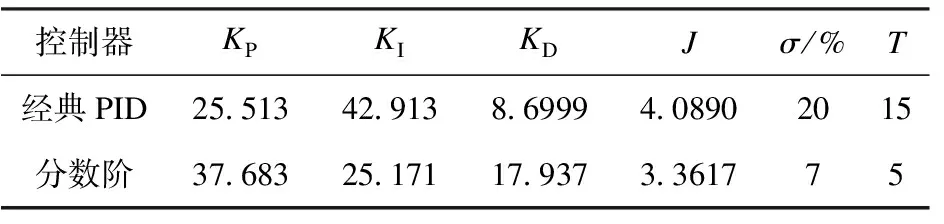
Grunwald-Letnikov分数阶微积分定义。对于任意的实数m, 对m取整,记为[m],其中[m] (1) (2) (2)Riemann-Liouville分数阶微积分定义 (3) 式中:m-1<α 分数阶PIλDμ控制器包含一个可调的积分阶次λ和微分阶次μ,λ和μ的取值范围是任意实数,这是它和整数阶PID控制器不同的地方。其传递函数可以表示如下: (4) 式中:KP、KI、KD这三个参数分别表示比例增益、积分常数和微分常数,它们通过线性组合构成控制量,控制被控对象,三个参数的选择直接影响控制效果。分数阶PIλDμ控制器能够通过选择合理的参数λ和μ来提高控制效果。相比于改变微分系数KD和积分系数KI,调整分数阶微积分的阶次λ和μ来改变控制效果更加明显。 图1为分数阶PIλDμ控制器的原理图。 图1 分数阶PIλDμ控制器结构原理图 图中:r(t)为系统输入;e(t)为误差;u(t)为控制器输出;y(t)为系统输出。 遗传算法不需要任何初始信息可以优化参数,能够快速有效地找到最优解。本文的自适应GA算法的基本过程如下: 采用随机遍历抽样的方法选择个体,通过单点交叉进行重组,通过变异产生新的个体,再计算新个体的目标函数值。文中运用Matlab和Simulink实现基于自适应遗传算法的分数阶PIλDμ控制器的参数整定,具体操作流程图如图2所示。 图2 遗传算法优化分数阶PIλDμ控制器参数流程图 遗传算法(GA)产生种群,首先该种群依次赋值给PID控制器的参数KP、KI、KD,对于λ和μ的选择是经过大量的人工实验验证的,得出最好的参数赋予它们。然后运行控制系统的Simulink模型,得到该组参数对应的性能指标,该性能指标再传递到遗传算法中作为该种群的适应值,最后判断是否可以退出算法。 2.1 对参数进行编码 在遗传算法中,首先选择运行参数,如个体数目L、最大遗传代数为M、变量的二进制位数Q(即对每一个参数用10位二进制串来表示);其次确定要寻优的PID控制器的参数范围,即KP、KI、KD;最后根据精度要求用一个二进制字串对对每个参数进行编码。 2.2 初始种群的确定 在生成初始种群时,为了更快的寻求最优解,一般根据经验确定目标函数的可能最优解。初始种群及其变化如图3~图6所示。 图3 初始种群分布图 图4 经过一次遗传迭代的结果 图5 经过10次遗传迭代的结果 图6 经过50次遗传迭代的结果 其中,在经过遗传算法优化迭代的过程中,KP、KI、KD的数值变化趋势如表1所示。 表1 KP、KI、KD的数值变化趋势 2.3 适应度函数的选取 PID参数优化的本质是通过优化KP、KI、KD这三个参数来达到求目标函数的最优值的目的。适应度值与选取的目标函数有关,首先需要对目标函数进行分配,其值表示个体对环境适应能力的强弱。本文选择用绝对误差积分模型(ITAE)来表示性能指标[6-7]: (5) 由于PID的参数优化问题是求目标函数的最小值,定义适应度函数为 (6) 2.4 遗传算子的自适应选择 采用改进的自适应方法对遗传算子(交叉算子Pc和变异算子Pv)进行选择。经典的自适应调整Pc和Pv的方法是由 Srinvivas等提出的,具体公式如下: (7) (8) k1、k2、k3、k4取(0,1)区间的值,分别为0.5、0.85、0.02、0.01可自适应调整。fmax表示最大种群的适应度值,favg表示每代种群的平均适应度值,f′表示要交叉的两个个体中的较大的适应度值,f为变异个体的适应度值。 上述方法可以看出,当适应度值越接近最大适应度值时,交叉概率和变异概率越小;当等于最大适应度值时,交叉概率和变异概率的值变为零。这种自适应方法比较适合群体处于进化后期,对进化初期不利,因为在进化初期群体中优良的个体大部分处在不变的状态,此时的个体不一定是优化的全局最优解,这容易陷入局部最优解。因此,为了使最大适应度个体的交叉概率和变异概率不为零,经过大量的实验,改进的自适应公式如下: (9) (10) 式中:Pc2为种群初始交叉概率;Pc1为提高后的种群交叉概率;Pv2为种群初始变异概率;Pv1为提高后的种群变异概率。为了使种群中拥有最大适应度值的个体的交叉概率和变异概率不为零,分别提高到Pc1和Pv1,这也就提高了表现优良个体的交叉概率和变异概率,使得它们不会处于停滞状态,从而使得算法跳出局部最优解,获得全局最优解。 为实现自适应调整,本文设定k1和k2取值范围为[0-1],Pc1为0.9,Pc2为[0.1-1]区间的值,Pv1为0.1,Pv2取[0.01-0.1]区间的值。 为验证本文提出的算法对分数阶系统的整定效果,选定文献[8]中的一个例子,被控对象用传递函数描述为 (11) 设定遗传算法的参数:KP、KI、KD∈[0,50]。个体数目L=30,最大遗传代数M=100,变量的二进制位数Q=10(即对每一个参数用10位二进制串表示)。 选择方法采用随机遍历抽样,它提供零偏差和最小个体扩展。Matlab程序运行得到30个个体的种群的适应度值为 V=[1.6552 1.1724 1.1034 1.7241 0.4828 1.9310 0.5517 1.4483 0.6897 1.8621 0.8276 0 1.5172 0.6207 2.0000 0.7586 1.3793 1.2414 0.2759 0.0690 0.9655 1.0345 0.8966 0.3448 0.1379 1.7931 0.4138 1.3103 1.5862 0.2069]T。 通过获得适应度向量V的累加和完成随机遍历抽样的表格。一个个体被选择的概率由下式给出: (12) 式中,f(xi)是个体xi的适应度,F(xi)是这个个体被选择的概率。这30个个体中第15代的适应度值为2.0000是最大的,因此它被选择的概率最大。 交叉采用单点交叉法,自适应算子的交叉和变异公式按照式(7~10),分别进行自适应调整。交叉概率为0.72,变异概率为0.048。为了更好地验证遗传算法,给出优化部分统计结果,取其中的十个个体,具体结果表示如下所示。 初始种群Z为 交叉变异后的新种群Z′为 采用Matlab平台进行仿真验证,系统的性能指标用绝对误差积分模型表示,可以利用Simulink构造适应度函数来获得相应的数值解。Simulink仿真框图如图7所示。 图7 自适应PIλDμ控制器参数优化的Simulink仿真框图 运行Simulink模型得到性能指标J:分数阶控制器的3.3617小于经典控制器的4.0890,说明对分数阶系统的整定效果,分数阶控制器优于经典控制器。 采用Matlab平台下的Simulink进行仿真,图8为优化PID得到的单位阶跃响应曲线。 图8 优化PID得到的单位阶跃响应曲线 图8说明,改进的自适应遗传算法在优化经典PID控制器时,对分数阶系统的控制效果不稳定,超调量大,达到20%,随着遗传代数的不断优化,在15代的时候达到稳定状态,即为调节时间T1。相比而言,改进的自适应遗传算法在优化分数阶PIλDμ控制器时,单位阶跃响应速度快,超调量小,只有7%左右,能更好地跟随阶跃信号,在第5代的时候已经达到稳定状态,即为调节时间T2。达到稳定状态的遗传代数越小表示调节时间越短,即T2远小于T1。调节时间反应了系统快速性,提高了系统的收敛速度。同时说明分数阶PIλDμ控制器更适合分数阶系统,能够很好地控制分数阶系统,保证系统的稳定性和收敛性。 综上,得到两种控制器整定分数阶系统的最优PID控制器参数、性能指标J、超调量σ和调节时间T(即达到稳定状态的遗传代数)如表2所示。 表2 PID控制参数和性能指标的最优解 用改进的自适应方法设计的经典PID控制器为 (13) 对积分阶次λ和微分阶次μ的取值范围为[0-1],经过大量实验得出最优的两个数值是λ=0.5和μ=0.9,此数据的选取能够满足系统的要求。 所以,分数阶PIλDμ控制器为 (14) 将经典PID控制器应用于分数阶系统时,用改进的自适应遗传算法对控制器的参数寻优存在超调量大,收敛速度慢的问题。而分数阶PIλDμ控制器应用于分数阶系统时,这种改进的方法解决了上述存在的问题,显著地降低了系统的超调量,提高了收敛速度,减少了收敛时间,并且使该系统更稳定。同时,仿真结果也表明,分数阶PIλDμ控制器更适用于分数阶系统。 [1]Vinagre B.M,Podlubny I,Hernandez A,et al.Some Approximations of Fractional Order Operators Used in Control Theory and Applications[J].FCAA Journal of Fractional Calculus & Applied Analysis,2000,(3):231-248. [2]Machado J.A.T.Discrete-Time Fractional-Order Controllers[J].FCAA Journal of Fractional Calculus & Applied Analysis,2001,(4):47-66. [3]Hu Haibo,Huang Yourui.The self-tuning fractional order PID controller which based on hybrid PSO neural network[J].Microelectronics & Computer,2010,27(5):157-161. [4]Li Wen,Liu Yang.Fractional order PIλDμcontroller parameters setting which based on genetic algorithm[J].Journal of dalian jiaotong university,2009,30(6):82-85. [5]Wang Jifeng.Control performance analysis for fractional order systems[M].Beijing:Publishing house of electronics industry,2010. [6]Niu Xiangjie,Wang Yujie,Tang Jian.PID controller parameters optimization research based on genetic algorithm[J].The computer simulation,2010,27(11):180-182. [7]Hadi Ramezanian,Saeed Balochian.Optimal design a fractional-order PID controller using particle swarm optimization algorithm[J].International journal of control and automation,2013,6(4):55-67. [8]F.Merrikh-Bayat,M.Karimi-Ghartemani. Method for designing stabilisers for minimum-phase fractional-order systems[J].IET Control Theory Appl.,2010,4(1):61-70. (责任编辑:马金发) An Adaptive PID Controller Parameter Optimizing Method of the Fractional-order System ZHANG Yanzhu, GE Zheng,WANG Yanmei (Shenyang Ligong University,Shenyang 110159,China) With the in-depth studying of fractional calculus theory,more and more complex system is more accurate characterization with fractional order model.However,when the classic controller method is applied to fractional order system,there will be slow convergence and large overshoot and other issues.Fractional order controller optimization problem is studied,on fractional order system.In this method,the integral absolute error model (ITAE) is taken as a performance indicator,and the introduction of genetic optimization algorithm is proposed for fractional order PIλDμcontroller parameter optimization,and then the improved algorithm is applied to optimize multiple parameters of fractional order PIλDμthrough adaptive selecting crossover and mutation probability.Simulation results show that fractional order PIλDμcontroller can be a good solution the problems for classical fractional order system controller,which improves system convergence speed and control performance. fractional order PIλDμcontroller;fractional order system;parameters optimizing;adaptive genetic algorithm 2014-07-07 辽宁省教育厅资助项目(L2013084) 张艳珠(1971—),女, 副教授,博士,研究方向:目标识别,分数阶控制,智能算法. 1003-1251(2015)02-0006-06 TP27 A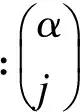
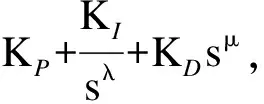
2 参数自适应GA算法
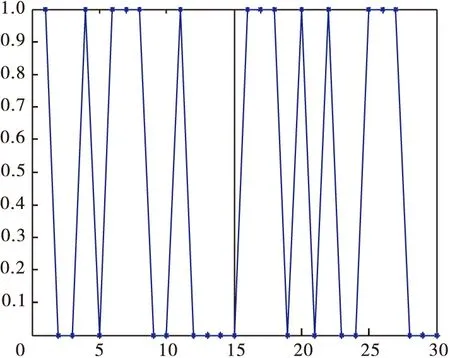
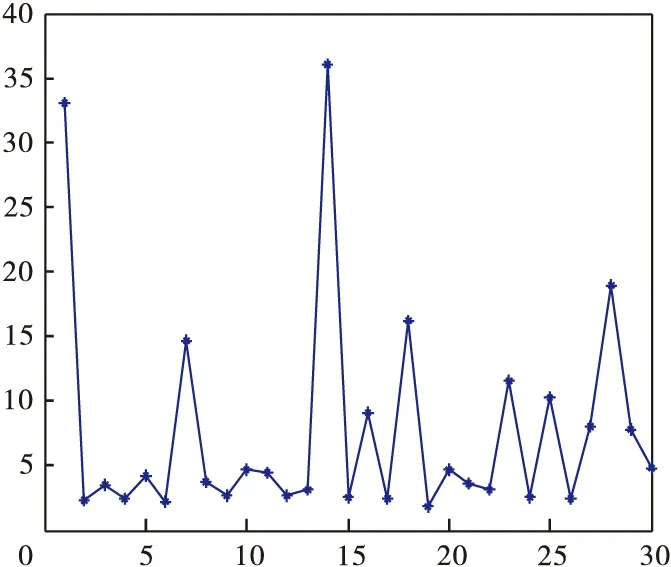
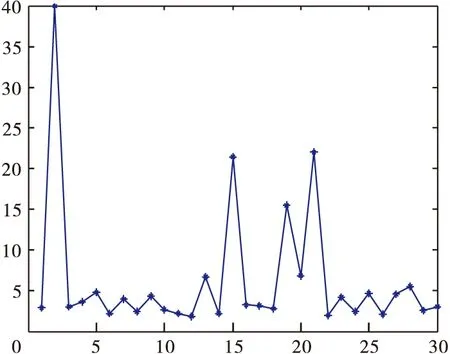
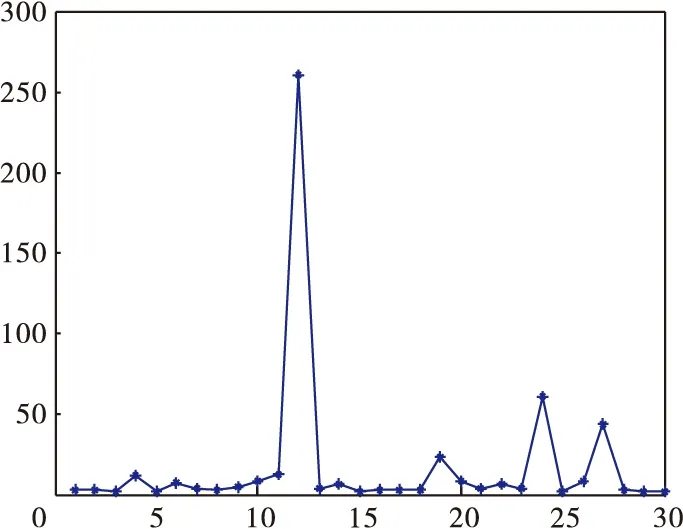
3 仿真实例

4 结论
