巧用临界条件解题——针对竖直平面内圆周运动中绳(环)模型
2015-02-20周晓峰
周晓峰
(江苏省淮安市新马高级中学,江苏 淮安 211700)
巧用临界条件解题——针对竖直平面内圆周运动中绳(环)模型
周晓峰
(江苏省淮安市新马高级中学,江苏淮安211700)
摘要:在变速圆周运动中的某些特殊位置上,常存在着最小(或最大)的速度,小于(或大于)这个速度,物体就不能再继续作完整的圆周运动了,此速度即为临界速度.在这个位置物体的受力必满足特定的条件,这就是临界条件.通过受力分析来确定临界状态和临界条件,是较常用的解题方法.
关键词:竖直平面;圆周运动;临界条件;模型
圆周运动是一种特殊的也是较为简单的曲线运动,无论是在竖直平面内的圆周运动还是在水平面内的圆周运动,都常出现临界问题.竖直平面内的圆周运动一般是典型的变速圆周运动(带电粒子在匀强磁场中的运动除外).在变速圆周运动中的某些特殊位置上,常存在着最小(或最大)的速度,小于(或大于)这个速度,物体就不能再继续作完整的圆周运动了,此速度即为临界速度.在这个位置物体的受力必满足特定的条件,这就是临界条件.当物体的受力发生变化时,其运动状态随之变化.当某力突然变为零时,对应物体将出现相应的临界状态.常见的如绳子突然断裂、支持物的作用力突然变化等.通过受力分析来确定临界状态和临界条件,是较常用的解题方法.现就竖直平面内圆周运动中绳(或环)模型出现的一些典型的论述如下.
1重力场中临界问题

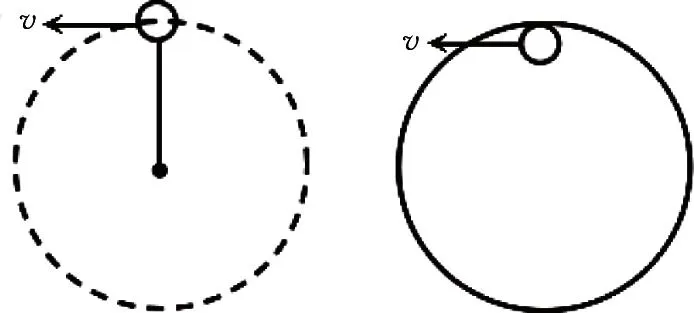
图1
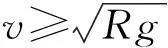

图2
例1如图2所示,小球被长为L的细绳静止地悬挂着,给小球多大的水平初速度,才能使绳在小球运动过程中始终紧绷?
解析:在小球运动过程中绳始终绷紧,有两种情况:

2电场中临界问题
电场中带电粒子在竖直平面内做圆周运动,临界状态在等效“最高点”或“最低点”:
(1)等效“最高点”:重力和电场力的合力与绳的拉力(或圆环轨道的支持力)在同一直线上,且方向相同,在此位置速度最小时,绳的拉力(或圆环轨道的支持力)为零;
(2)等效“最低点”:物体速度最大,绳的拉力最大,重力和电场力的合力与绳的拉力在同一直线上,且方向相反.
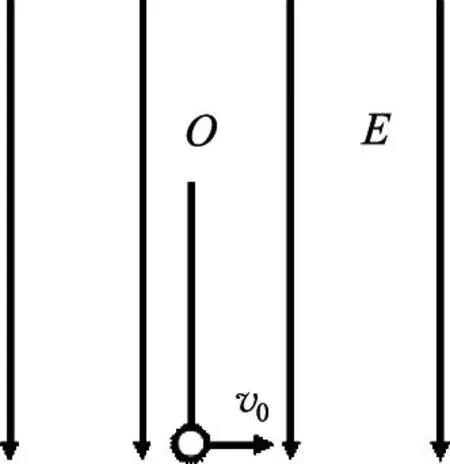
图3
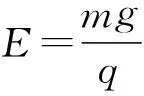

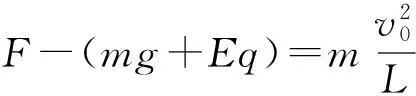
变式:若上题中的匀强电场方向是水平向右,电场强度不变,使小球做完整圆周运动,求在最低点时施给小球水平初速度v0应满足什么条件?小球在运动中细线受到的最大拉力应满足什么条件?

图4
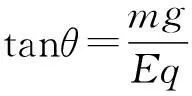

3小结
在竖直平面内的圆周运动运动中,轻绳只能对物体产生沿绳收缩方向的拉力,圆环轨道只能对物体提供支持力,在最高点对物体作用力为零时是临界条件.在处理带电小球在竖直平面内的圆周运动时,临界条件的最高点有时并不是圆轨道的几何最高点,而是在等效“最高点”,即重力和电场力的合力与绳的拉力(或圆环轨道的支持力)在同一直线上,且方向相同.因而临界条件的判断关键是寻找最高点,临界条件找准了,相应问题也就自然解决了.
