颅骨对磁感应断层成像信号检测影响的仿真与实验研究

柯 丽 李盼盼 陈 红 刘 欢 杜 强

(沈阳工业大学电气工程学院，沈阳 110870)



颅骨对磁感应断层成像信号检测影响的仿真与实验研究

柯 丽*李盼盼 陈 红 刘 欢 杜 强

(沈阳工业大学电气工程学院，沈阳 110870)

采用仿真和实验研究颅骨对磁感应断层成像(MIT)信号检测的影响。使用Comsol软件建立3层球形仿真颅脑模型，仿真计算颅骨电导率对MIT信号检测的影响。使用螺线管线圈、后置电路及数据接收仪器搭建单通道磁感应信号测量实验系统，利用琼脂和NaCl溶液制作与真实颅脑电导率分布相近的脑出血分层模型，模型外径为158 mm；最后采用有颅骨和无颅骨两种模型，测量无病变及不同病变位置情况下MIT信号的相位变化，模型中心与检测线圈相距85 mm。实验结果显示，在无病变和病变分别位于X-Y平面上坐标为(-40,0)、(0,0)和(40,0)的位置时，有、无颅骨数据的幅值比例分别为0.57、0.59、0.42、0.61，其中，坐标点(-40,0)代表Y轴左侧距离激励线圈45 mm的位置，坐标点(40,0)代表Y轴右侧距离接收线圈45 mm的位置。当病变存在时，有、无颅骨数据的变化趋势均为：病变位于坐标点(-40,0)时最大，病变位于坐标点(40,0)时次之，病变位于坐标点(0,0)时最小。实验结果表明，颅骨对MIT信号的数据大小有衰减作用，但不影响数据的变化趋势，提示在实际应用中结合高精度检测设备，可实现颅内病变的无创、无接触图像监测。

磁感应断层成像 (MIT)；颅骨；脑出血模型；仿真；琼脂模型

引言

磁感应断层成像(magnetic induction tomography, MIT)是电阻抗断层成像(electronic impedance tomography, EIT)技术的分支[1]，其特点是激励和测量环节与被测对象没有直接的接触。人体头部阻抗成像是MIT技术应用的一个重要方面。2000年，Ostendorp等[2]进行了生物体的在体测量与离体测量，并且给出了头皮、颅骨和脑组织的电导率比值为1∶1/15∶1。由此可以看出，颅骨的电导率较低，将会使被测物周围的涡流磁场产生衰减，从而严重影响成像效果。因此，国内外有多个科研小组都开展了相关的研究。1999年，英国Holder小组[3]用盐水槽模拟头皮和脑，石膏环模拟颅骨，使用磁共振方法，分析了有、无石膏环情况下的电流分布。2003年，Holder[4]建立了球形容器，由两个通过橡胶圈和螺栓相连的有机玻璃半球壳构成。银球电极放于球形的内面，用牙科级的熟石膏制成的球壳模拟颅骨，容器内装满饱和的硫酸钙溶液，用来防止仿真颅骨溶解。溶液的电导率为0.25 S/m，浸入溶液中的仿真颅骨电导率为0.012 S/m。王聪等[5]于2007年建立了圆筒形和简单球形的均值颅骨电导率分布头模型，对含有多种扰动目标的模型进行了成像研究。2008年，Dekdouk等[6]采用头部形状的球模型，分析了单通道磁感应成像系统对中心水肿区域的敏感性。其模型采用分层的形式，包括头皮、颅骨、脑脊液、脑灰质和脑白质。2011年，李建波等[7]使用硬石膏首次建立了近似真实形状和非均匀电阻率分布的颅骨模型。通过国内外的研究可以发现，目前的研究已经使用软件仿真的方式，或者使用有机玻璃或石膏制作颅脑模型的具体实验方式，指出颅骨对MIT信号的检测会产生影响，但却没有给出对相位差检测产生影响的具体结果。本研究搭建了一套单通道磁感应信号检测实验系统，使用琼脂与NaCl溶液制作符合真实颅脑电导率分布的三层颅脑模型，设计有、无颅骨情况下，检测不同病变位置所产生相位差的实验，研究颅骨对MIT信号检测的影响，给出了相关结论。

1 材料和方法

1.1 颅骨对MIT信号检测影响的仿真

1.1.1 MIT相位检测原理

磁感应断层成像(MIT)的基本工作原理是：在位于目标外围的线圈组或者线圈阵列中的一个线圈上施加激励电流，这时被测目标导体内部会感应出涡旋电流，涡流会产生出感应磁场，通过放置在目标外围的其他检测线圈，测量与目标导体电导率参数信息相关的感应磁场[8-9]，如图1[10]所示。

图1 MIT工作原理Fig.1 Working diagram of MIT

如图2所示，在激励线圈中施加交变电流，从而产生交变磁场B，该交变磁场又会在被测对象中感应出交变涡流，涡流的分布与被测对象电导率分布σ直接相关，该交变涡流又会感应出交变磁场ΔB，使用测量线圈检测激励磁场B和感应磁场ΔB的叠加场B+ΔB。当被测对象内部的电导率分布发生变化时，感应磁场ΔB也会发生变化[8]。 Griffiths 等通过理论分析认为，ΔB的实部由位移电流引起，只与目标物的介电常数有关，ΔB的虚部由涡流感生，与目标物的电导率σ及激励频率ω的大小成线性关系，即 ΔB/B∝ -ω2ε+ iωσ，由此电导率σ反映在 ΔB/B的虚部中。因此，在实验时需要检测的是包含被测目标物内部电导率信息的感应磁场的虚部[9]。若把B作为参考信号，则电导率σ反映在 ΔB引起的相位变化 Δφ中，Δφ可以通过检测线圈和相位检测电路得到，通过测量Δφ即可得到电导率的变化规律。

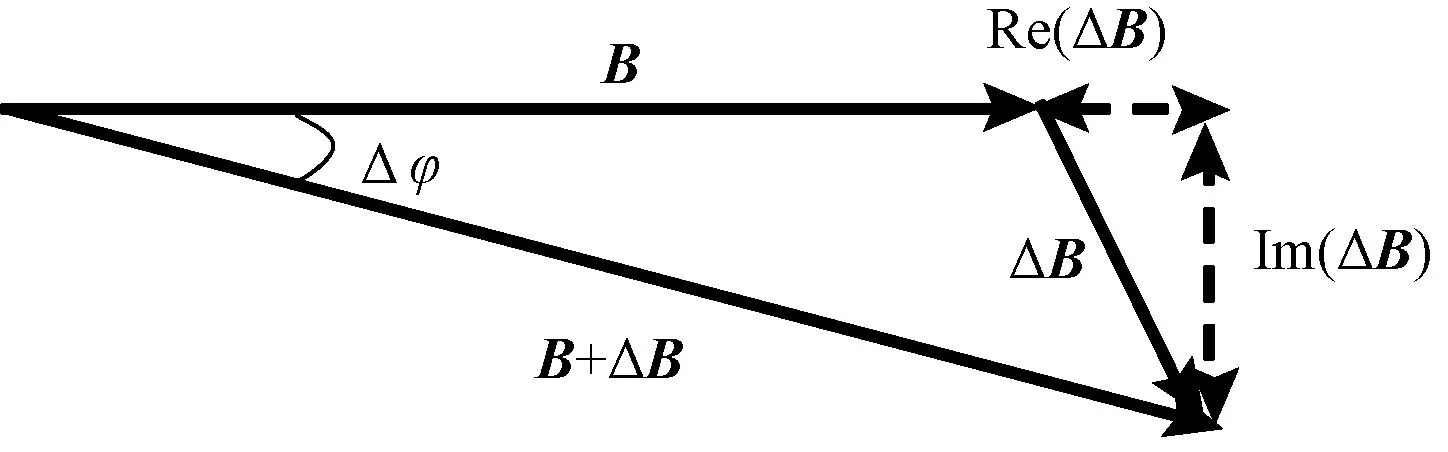
图2 激励磁场与感应磁场的矢量关系Fig.2 Vector diagram of excitation and induced magnetic field

1.1.2 颅骨电导率对MIT信号检测影响的仿真计算

近几年学者们一直在检测颅脑各组织的电导率值，但是一直没有统一的结论，因为生物体的电特性容易受到生物体状态，温度以及环境的影响。

本研究依据天津大学王湘嵛论文[11]中所提到的300 kHz时的数据，进行颅脑不同层次电导率的设计，其具体数据如表1所示。

表1 300 kHz下脑组织的电导率及介电特性

图3 三维颅脑模型Fig.3 Three dimensional head model

根据表1，在Comsol软件中建立颅脑模型，研究颅骨对MIT检测数据的影响。

首先，模拟三层球形颅脑模型，如图3所示，由外而内分别为颅骨层、脑膜层和内颅层；三层的外径分别为158.0、148.0和144.0 mm。其中，脑膜层和内颅层电导率固定，均为0.2 S/m。颅骨层的电导率分为两种：0.2 S/m和0.02 S/m。当电导率为0.2 S/m时，模拟的是无颅骨的状态；当电导率为0.02 S/m时，模拟的是有颅骨的状态。

其次，选择“准静态，磁”模块中的时谐分析，频率设置为300 kHz，网格剖分中的网格点数为5 636，单元数为31 626。加入激励线圈后，从激励线圈开始，在最外层边界上每10°设为一个数据检测点，提取36个边界检测点处的磁感应强度相位，得出颅骨电导率对MIT信号的影响如图4所示。可以看出，有、无颅骨状态下，磁感应强度相位的变化趋势基本一致，说明颅骨在MIT信号测量中并不会改变测量结果的变化趋势。但是，由于颅骨的电导率与其他脑组织相比极低，会使被测物周围的涡流磁场产生衰减，从而对MIT信号的大小产生影响。因此，有必要设计实验，系统详细地研究颅骨对磁感应信号的影响。

图4 颅骨电导率对MIT信号的影响Fig.4 Influence of conductivity of skull to MIT

1.2 单通道磁感应信号测量系统

基于MIT成像原理，设计了一套单通道磁感应信号测量系统，系统框图如图5所示。系统包括3个模块：信号发生模块，使用的是信号发生器DG4102；信号检测模块，由激励线圈、检测线圈、信号处理电路三部分组成；信号接收模块，使用的是锁相放大器SR844及内部采集软件。

图5 磁感应信号测量系统框图Fig.5 Diagram of magnetic induction signal measuring system

1.2.1 磁感应线圈

磁感应线圈包括激励线圈和检测线圈。磁感应信号测量系统将正弦交变电流通入激励线圈，产生激励磁场，将激励源信号分布到整个测量区域，再由检测线圈检测涡流信号，并将信号传送到信号处理电路及接收仪器中。考虑磁场的均匀性和线圈的几何外形接近系统的数学模型，选用螺线管线圈；在激励源提供足够大电流的前提下，选择匝数n较多，截面积S较大的激励线圈可以提供较强的激励磁场，便于检测。在满足检测敏感度的前提下，选择长宽尺寸较小(即截面积S较小)且匝数n较多的检测线圈，这样可以减小理论模型的计算误差，改善目标的定位精度。在这种情况下，设计线圈参数，并改进激励源和检测电路的设计，相关参数如表2所示。

表2 激励与接收线圈的相关参数

1.2.2 信号处理电路

生物组织的电导率通常在0.02～2.0 S/m的范围内[12]，生物组织在磁场激励下产生的涡流磁场信号非常微弱，所以被检测信号的相位变化也非常微小。为了能准确检测到信号，本研究设计的检测电路包括滤波和放大两个部分：差分放大滤波电路和仪用差分放大电路。

使用LT6600-20全差分滤波运算放大芯片完成差分放大滤波电路，放大部分采用差分放大避免了接地信号的干扰，滤波部分分别采用近似4阶切比雪夫(Chebyshev)低通滤波器，截止频率为20 MHz，提供76 dB的信噪比，放大倍数为402 Ω/Rin，输入电阻并联62 pF电容以匹配滤波频率。检测线圈的信号经前置滤波放大电路，去除高频噪声，得到初级放大，信号保持差分信号形式。

采用仪用放大器对初级信号进行放大，消除共模信号，对差分信号进行放大。仪用放大器线性误差较小，具有高输入阻抗和低噪声的特性，适用于本信号的差分放大。使用AD8130精密高速仪用放大器，将差分信号放大后转变成单端信号输出，以便进行相位检测。该芯片在工作频率范围内提供70 dB的共模抑制比，差模输入阻抗1 MΩ，最大输入共模电压±8.4 V，增益带宽为270 MHz，其内部采用三运放结构，包括两个高输入阻抗同相放大器和一个差动放大器，这种结构可以对信号进行很好测量，并将输出转为单端信号，适用于鉴相电路处理。

1.2.3 鉴相模块

相位差测量使用的仪器是斯坦福大学研究的射频锁相放大器SR844。这是本研究实现高精度相位差检测的关键器件，其检测频率范围为25 kHz～200 MHz。采用相敏检测技术(PSD)锁住具有相同频率的信号，而抑制不同频率的信号，相位分辨率为0.02°。

1.3 三层颅脑琼脂模型设计

1.3.1 颅脑模型的制作

在研究中，将颅脑由外而内分为颅骨层、脑膜层和内颅层，三层的厚度分别为5.0、2.0和72.0 mm，其电导率参数如表3所示。

表3 实验中的分层参数

由表3给出的数据，计算出内颅、脑膜及颅骨所需琼脂及NaCl溶液的量。

首先，制作电导率为0.2 S/m的内颅琼脂模型。

步骤1：将琼脂和电导率为0.2 S/m的NaCl溶液放入烧杯中，比例为琼脂: NaCl=0.8 g: 100 mL。

步骤2：将烧杯放入微波炉中加热至沸腾，用玻璃棒搅拌，使琼脂粉充分溶解，制成琼脂液。

步骤3：将制作好的琼脂液倒入口径为145.0 mm、高为72.0 mm的半球形模具中，冷却后成型。

其次，制作颅骨层及脑膜层。

步骤1：将琼脂和电导率为0.02 S/m的NaCl溶液、琼脂和电导率为0.2 S/m的NaCl溶液分别放入烧杯中，比例均为琼脂: NaCl=0.8 g: 100 mL。

步骤2：分别将烧杯放入微波炉中加热至沸腾，使琼脂粉充分溶解，制成琼脂液。

步骤3：将琼脂液放入模具中，制成规定厚度的薄层。

最后，将制作好的颅骨层和脑膜层无缝隙地贴合在内颅琼脂模型上，并将颅骨层和脑膜层多余的部分去掉，制成的三层颅脑模型剖面如图6所示。

图6 三层颅脑模型剖面Fig.6 The three layer head model profile

1.3.2 脑出血病变位置设计

三层颅脑模型的3个病变位置如图7所示，1号位置对应病变位于后脑，2号位置对应病变位于颅脑中心位置，3号位置对应病变靠近前额，分别对应X-Y平面上坐标为(-40,0)、(0,0)和(40,0)的位置。

图7 所测颅脑病变位置Fig.7 Lesion location of measured brain model

实验时，在颅脑模型的1、2、3位置分别放入一个底面直径为15 mm、长度为24 mm、电导率为2.0 S/m的圆柱状琼脂块仿真病变组织。为使检测效果更加明显，这一电导率大于血液在300 kHz下的0.72 S/m，且扩大了1.8倍。如图8所示，为使病变位置容易辨认，用红色进行标注。

图8 实验病变位置。(a)无病变；(b)1号位置；(c)2号位置；(d)3号位置Fig.8 Map of experimental lesion locations. (a) No lesion;(b) Position 1; (c) Position 2; (d) Position 3

1.4 实验过程

将制作好的颅脑模型作为有颅骨实验组，再在对照组中制作一个与实验组外径尺寸相同、电导率为0.2 S/m的半球形无颅骨颅脑模型。

在两组模型内设置一个底面直径为15 mm、高为24 mm的圆柱形琼脂块作为仿真的病变组织，圆柱位于模型的X-Y平面上，电导率为2.0 S/m，分别放置于坐标点为(-40,0)、(0,0)和(40,0)的位置，如图8所示。

在实验过程中，激励频率为300 kHz。激励线圈与检测线圈中轴线相距170 mm，被测物与检测线圈相距85 mm。在软件鉴相平台中，设置采样率为8 Hz，采样时间为30 s，由于数据采集软件溢出的影响，最终的采样点数为242。

实验系统如图9所示。激励线圈、被测物及检测线圈固定在高100 mm的木制支架上，被测物位于两线圈之间。信号发生器输出两路同步正弦信号：一路经过激励单元产生激励磁场，20 V，300 kHz，激励磁场穿过被测物，被检测线圈检测，检测信号经过相位差检测单元，由锁相放大器SR844采集；另一路作为参考信号，直接由锁相放大器SR844采集，2V，300 kHz。

图9 实验系统Fig.9 The experimental system

1.5 实验数据的采集与处理

由于存在随机误差，采用多次测量求平均值的方法予以消除。为减小检测通道相位漂移对检测结果的影响，每个被测目标的测量时间应尽可能短。通过软件鉴相平台，检测由被测物产生的相位变化。

步骤1：将无病变的颅脑模型放入系统中测量，此时的相位数据242个。

步骤2：将无病变的颅脑模型移出系统，测量此时空场的相位数据242个。

步骤3：分别求取步骤1和步骤2中242个数据的平均值后做差，得出无病变时的相位变化。

步骤4：将有病变的颅脑模型放入系统中，测量此时的相位数据242个。

步骤5：将有病变的颅脑模型移出系统，测量此时空场的相位数据242个。

步骤6：分别求取步骤4和步骤5中242个数据的平均值后做差，得出有病变时的相位变化。

步骤7：将步骤3和步骤6所得的数据结果做差，取绝对值，从而得到最终结果。

通过以上方法，可以减小相位噪声和系统误差带来的影响。相位差计算公式如下：

(1)

(2)

(3)

2 结果

将无颅骨与有颅骨颅脑模型放置于实验系统中，测量固定体积情况下无颅骨与有颅骨时无病变及3个位置(1号位置、2号位置、3号位置)病变所引起的相位变化。经SR844锁相放大器测量和接收数据，对数据进行处理，实验结果如表4所示。

表4 有、无颅骨时无病变及3个位置病变的相位变化

表4中，第1列代表实验中4种测量情况，由上至下分别对应无病变、病变位于坐标点(-40,0)、病变位于坐标点(0,0)以及病变位于坐标点(40,0)。第1列和第3列分别代表无颅骨存在和有颅骨存在时MIT信号的相位变化值，为了方便比较，这两列均取相位变化的绝对值，可以看出，在有、无颅骨存在时，系统能够检测到0.02°以上的相位变化值。第4列是将有颅骨时的相位变化值与无颅骨时的相位变化值做差，发现有颅骨时的相位变化值小于无颅骨时的相位变化值。

在无颅骨和有颅骨两种情况下，相位变化幅值对比结果如图10所示。

图10 无病变与3个位置病变相位变化Fig.10 Phase difference of no lesion and three positions lesions

在图10中，横坐标代表的是实验中所测的4种情况，由左至右分别表示无病变、病变分别位于坐标点(-40,0)、(0,0)和(40,0)，纵坐标代表4种情况下MIT信号相位变化的幅值。灰色表示无颅骨时的相位变化值，黑色表示有颅骨时的相位变化值。由第2组～第4组的数据可以看出，当有病变存在时，有、无颅骨时相位差变化的趋势均为：病变位于1号位置时最大，病变位于3号位置时次之，病变位于2号位置时最小。由第1组数据与其余3组数据相比较可以看出，有病变存在时的相位变化值明显高于无病变存在时的相位变化值。将每组数据中的两个数据进行比较，可以看出，无病变和病变分别位于坐标点(-40,0)、(0,0)和(40,0)时，有、无颅骨数据的幅值比例分别为0.57、0.59、0.42和0.61。

3 讨论

在由激励线圈和接收线圈组成的磁感应系统中，交流电流通入激励线圈产生激励磁场，激励磁场围绕在激励线圈周围，所以越靠近激励线圈的位置磁场越大。接收线圈上检测到的是由激励磁场产生的二次涡流磁场，越靠近接收线圈磁场越大。但是，由于接收线圈周围是感应磁场，所以其大小势必小于激励线圈周围的激励磁场。在激励与接收线圈中轴线的中点上，由于激励磁场与感应磁场的相互抵消作用，使得这点的磁场远小于激励线圈和接收线圈周围的磁场。综上所述，在磁感应系统中，信号的大小关系为：靠近激励线圈的磁场最大，靠近接收线圈的磁场次之，激励与接收线圈中轴线中点处的磁场最小。

颅骨的电导率比头皮和脑组织的电导率低得多，这使得颅脑周围的涡流磁场产生衰减，从而降低了系统对颅内阻抗信号的敏感度。由表4可以看出，测量线圈上有颅骨时的相位变化值小于无颅骨时的相位变化值，有、无颅骨时，系统能够检测到0.02°以上的相位变化值，这充分证明了系统的可用性。

由图10可以看出，有病变存在时的相位变化值明显高于无病变存在时的相位变化值，表明系统可以检测到颅脑深层电导率的变化。当有病变存在时，有、无颅骨数据的变化趋势均为：病变位于坐标点(-40,0)时最大，病变位于坐标点(40,0)时次之，病变位于坐标点(0,0)时最小，即病变靠近激励线圈时最大，病变靠近接收线圈时次之，病变位于原点时最小，这与磁场的分布规律一致。在无病变和病变分别位于坐标点(-40,0)、(0,0)和(40,0)时，有、无颅骨数据的幅值比例分别为0.57、0.59、0.42和0.61，可以看出有颅骨时的MIT信号相位变化幅值明显小于无颅骨时的相关幅值，这与仿真结果一致。

实验结果表明，虽然颅骨的存在改变了所测数据幅值的大小，但有、无颅骨时的数据变化趋势并没有变化。这提示，颅骨的存在虽然降低了检测信号的幅度，但系统却能有效地检测到病变的存在，显示了MIT测量可“穿透”颅骨的特性，从而验证了MIT在颅脑功能图像重建方面的优势。

在研究过程中，充分考虑到真实颅脑结构中，脑膜与内颅之间的间隙可能会对MIT信号检测产生影响，所以，制作模型时，将电导率十分相近的脑膜和内颅分为2层，并将电导率均设置为0.2 S/m。将整个颅脑模型分为3层，能使其更加符合实际情况，令实验结果更加准确。

研究中，根据琼脂和NaCl溶液制作的模型近似为纯电阻材料，忽略了人脑各部分相对介电常数对实验结果及其后图像重建的影响；由于琼脂材料特性和实验手段的限制，目前的分层琼脂颅脑模型还比较粗糙，只进行了定性分析。下一步将设计更加精确的琼脂颅脑模型实验方案，以便提高测量精度，实现定量分析。

4 结论

MIT是一种成像技术，MIT信号的检测是图像重建的重要基础。本研究使用仿真和实验的方法，探讨了颅骨的存在对MIT信号检测的影响。使用Comsol软件，建立三层球形仿真颅脑模型，仿真计算了颅骨电导率对MIT信号检测的影响。利用琼脂与NaCl溶液，制作模拟真实颅脑电导率分布的分层颅脑仿真模型，构建磁感应信号测量系统，对无病变及3个不同部位病变的模型进行实验研究。研究结果显示，有病变存在时的MIT信号相位变化值明显高于无病变存在时的相位变化值；当有病变存在时，有、无颅骨数据的变化趋势均为：病变位于坐标点(-40,0)时最大，病变位于坐标点(40,0)时次之，病变位于坐标点(0,0)时最小；在无病变和病变分别位于X-Y轴上坐标点为(-40,0)、(0,0)和(40,0)的位置时，有、无颅骨数据的幅值比例分别为0.57、0.59、0.42和0.61。

研究结果表明，磁感应断层成像系统能够检测到颅脑深层的电导率变化，虽然颅骨对MIT信号的检测有衰减作用，但并不影响数据的变化趋势。MIT利用磁场作用测量电导率及其变化，比较容易耦合进入颅骨内部，有利于MIT用于颅脑疾病的检测与成像中，结合高精度硬件检测设备，可实现颅内病变的无创、无接触图像监测。

[1] Al-Zeibak S, Saunders NH. A feasibility study ofinvivoelectromagnetic imaging [J]. Phys Med Biol, 1993, 38(3): 151-160.

[2] Thom FO, Jean D, Dick F,etal. The Conductivity of the human skull: results ofinvivoandinvitromeasurements [J]. IEEE Trans Biomed Eng, 2000, 47(11): 1487-1491.

[3] Humberto RG, Richard B, David H,etal. Measurement of electrical current density distribution in a simple head phantom with magnetic resonance imaging [J]. Phys Med Biol, 1999, 44(6): 281-291.

[4] Hamid D, Colin DB, David SH,etal. Electrical impedance tomography of human brain function using reconstruction algorithms based on the finite element method [J]. Neuroimage, 2003, 20(2): 752-764.

[5] 王聪，董秀珍，史学涛, 等. 基于电阻抗成像的均质头模型研究 [J]. 航天医学与医学工程, 2007, 20(1): 19-23.

[6] Dekdouk B, Pham MH, Armitagel DW,etal. A feasibility study on the delect ability of edema using magnetic induction tomography using an analytical model[C]//Dekdouk B, Pham MH, eds. European Conference of the International Federation for Medical and Biological Engineering. Berlin: Springer- Verlag. 2008: 736-739.

[7] 李建波. 近似真实形状和非均匀电阻率分布的头部物理模型的建立及其实验研究 [D]. 西安: 第四军医大学, 2011.

[8] 何为，王俊锋，徐征，等. 多通道开放式磁感应成像测量系统研究 [J]. 中国生物医学工程学报, 2010, 29(6): 877-881.

[9] Watson S, Williams RJ, Gough W,etal. A magnetic induction tomography system for samples with conductivities below 10 S·m-1[J]. Meas Sci Technol, 2008, 19(4): 1-11.

[10] 赵璐璐，柯丽. 颅脑阻抗特性三维建模及磁感应成像仿真研究 [D]. 辽宁: 沈阳工业大学，2013.

[11] 王湘嵛. 基于介电特性脑血肿检测的初步研究 [D]. 天津：天津大学, 2007.

[12] 柯丽，庞佩佩，杜强，等. 基于伽辽金有限元法的磁感应断层成像正问题仿真 [J]. 中国生物医学工程学报, 2012, 31(1): 53-58.

Simulation and Experimental Research on the Impact of Skull in Magnetic Induction Tomography Signal Detection

Ke Li*Li Panpan Chen Hong Liu Huan Du Qiang

(SchoolofElectricalEngineering,ShenyangUniversityofTechnology,Shenyang110870,China)

The aim of this paper is to study the effect of skull to magnetic induction tomography (MIT) signal detection through simulation and experiments. Firstly, a spherical brain model of three layers was established using Comsol software to simulate the effects of the skull conductivity to MIT signal detection. And then a multi-channel magnetic induction tomography experimental system which consists of solenoid coil, rear circuit and data receiving apparatus was established, and a hierarchical model of cerebral hemorrhage was made of agar and NaCl solution which has a similar conductivity distribution with the real brain. The diameter of the model is 158 mm. Finally, in the two models with skull and without skull, the phase change of no lesion and different locations of simulating lesions were measured. The distance between the model center and detection coil is 85 mm. From the results, what can be seen is that, when the model with no lesion and lesions were on the coordinates of (-40,0), (0,0) and (40,0) of theX-Yplane, the proportion of the phase change between the models with and without skull is 0.57, 0.59, 0.42, 0.61 respectively. The coordinates of (-40,0) and (40,0) represent the position which has a distance of 45mm from incentive coil to y axis and a distance of 45mm from Y axis to incentive coil respectively. When there is a lesion, the change trend of the data in the model with and without skull is same, which means that the maximum appears on the coordinate of (-40,0), the second appears on the coordinate of (0,0), and the smallest appears on the coordinate of (40,0). The results show that, the skull has an effect of attenuation on the size of MIT signals, but the changing trend of measured data is not changed. The results also indicate that the image detection of intracranial lesions can be achieved without a record and contact using high precision hardware detection system in practical applications.

magnetic induction tomography (MIT); skull; model of cerebral hemorrhage; phase difference; simulation; agar model

10.3969/j.issn.0258-8021. 2015. 05.007

2015-05-20， 录用日期:2015-08-27

国家自然科学基金(51377109)；辽宁省自然科学基金(2013020050)；辽宁省教育厅重点实验室基础研究项目(LZ2014011)

R318

A

0258-8021(2015) 05-0566-08

*通信作者(Corresponding author)， E-mail: ke.l@live.cn