合成孔径序列波束形成轴向运动补偿方法

孟晓辉 理 华 王君琳

(中国科学院声学研究所，北京 100190)



合成孔径序列波束形成轴向运动补偿方法

孟晓辉 理 华*王君琳

(中国科学院声学研究所，北京 100190)

合成孔径序列波束方法是一种新颖的医学超声成像方法，采用两个阶段的波束形成，在传统的超声成像系统中实现合成孔径成像，在不需要存储和传输大量射频回波数据的情况下，提高医学超声图像的分辨率。该方法的前提是假设成像目标静止不动，而通过仿真分析发现运动会造成成像目标位置错误。针对此问题，提出一种合成孔径序列波束形成运动估计和补偿方法：首先通过在同一位置连续发射接收两次以获取用于运动估计的数据，然后采用互相关方法对第一阶段波束形成得到的低分辨率图像进行运动估计和补偿，再对其做第二次波束形成得到高分辨率图像。Field II仿真结果显示，所提出的运动补偿方法可以得到正确的目标位置。对于运动速度为0.1 m/s的点目标，运动补偿后的平均横向分辨率与静止点目标相比仅降低2.03%，对比度降低2.7 dB。对于运动速度为0.2 m/s的囊目标,运动补偿后图像的对比度分辨率较静止情况仅降低8.53%，进一步说明所提出的运动补偿方法有效。

合成孔径；合成孔径序列波束形成；运动补偿

引言

医学超声成像与同位素扫描、核磁共振成像(MRI)以及计算机 X 射线层析成像(CT)构成现代医学影像诊断的4项主要检查方法，并且较其他几种成像方式而言，具有无创、实时、诊断成本低等特点，目前已经成为许多临床疾病诊断的首选方法[1]。合成孔径技术于上个世纪60年代后期被应用到超声成像领域[2]。90年代以前，合成孔径技术多数是用于无损检测领域，仅有少数用于医学超声的研究[3-4]。Nikolov 的博士论文专门论述了合成孔径医学超声成像[5]。 目前在医学超声成像中，较为常用的合成孔径技术为合成发射孔径(STA)方法[4]，即通过单阵元发射、全孔径接收，经波束形成得到低分辨率图像(LRI)，再通过将所有发射阵元得到的LRI相干相加得到高分辨率图像(HRI)。由于HRI对发射和接收都实现了动态聚焦，所以其较传统的超声成像方法就有更高的分辨率[6]。但是，这种发射合成孔径成像方法面临3个主要问题：一是单阵元发射造成的穿透性差和回波信号信噪比低；二是被测组织的运动会降低低分辨率图像间的相干性，从而影响成像质量；三是系统实现过程中需要存储和传输大量的射频回波(RF)线，系统复杂度很高。

对于上述3个问题，目前有多种改进方法,比如：为了改善单阵元发射造成的穿透性差和回波信号信噪比低的问题，可以采用多阵元模拟发射球面波和编码发射方法来解决[7-8]；对于低分辨率图像间运动影响成像质量的问题，也提出了多种运动补偿方案[9-10]；稀疏合成孔径是降低系统复杂度的一种方法[11-12]。此外，合成孔径序列波束形成[13]，也是一种改善系统复杂性高问题的重要方法。

合成孔径序列波束形成方法是一种分两个阶段进行的波束形成成像方法，可以采用传统的线阵列探头实现B模式成像。第一个阶段是采用传统的线性扫描方式，多阵元单焦点聚焦发射。对于多个阵元接收的RF数据进行单焦点波束形成，得到一条扫描线，发射和接收的焦点相同。这些焦点可以理解为虚拟发射源和虚拟接收源，构成一个虚拟阵列。第二个阶段的波束形成以第一阶段得到的扫描线为输入，利用虚拟阵列进行延时相加做第二次波束形成。合成孔径序列波束形成方法由于不需要存储和传输大量的单阵元接收的RF线数据，其实现复杂度较合成发射孔径方法大大降低。此外，由于是多阵元发射，所以也不存在合成发射孔径方法单阵元发射造成的穿透性差和回波信号信噪比低的问题，因此这种方法近年来得到很多学者的重视。但是，作为一种合成孔径方法，其中仍然存在被测组织运动影响成像质量的问题。

组织位移可以分解为横向分量和轴向分量，有研究表明影响合成孔径成像质量的主要是轴向位移分量[14]。笔者提出一种合成孔径序列波束形成的轴向运动补偿方法，并对该方法的效果进行了仿真分析，结果表明该方法可以有效地进行运动补偿，从而提高了成像质量。

1 方法

1.1 合成孔径序列波束形成方法的原理

合成孔径序列波束方法的原理如图1所示。

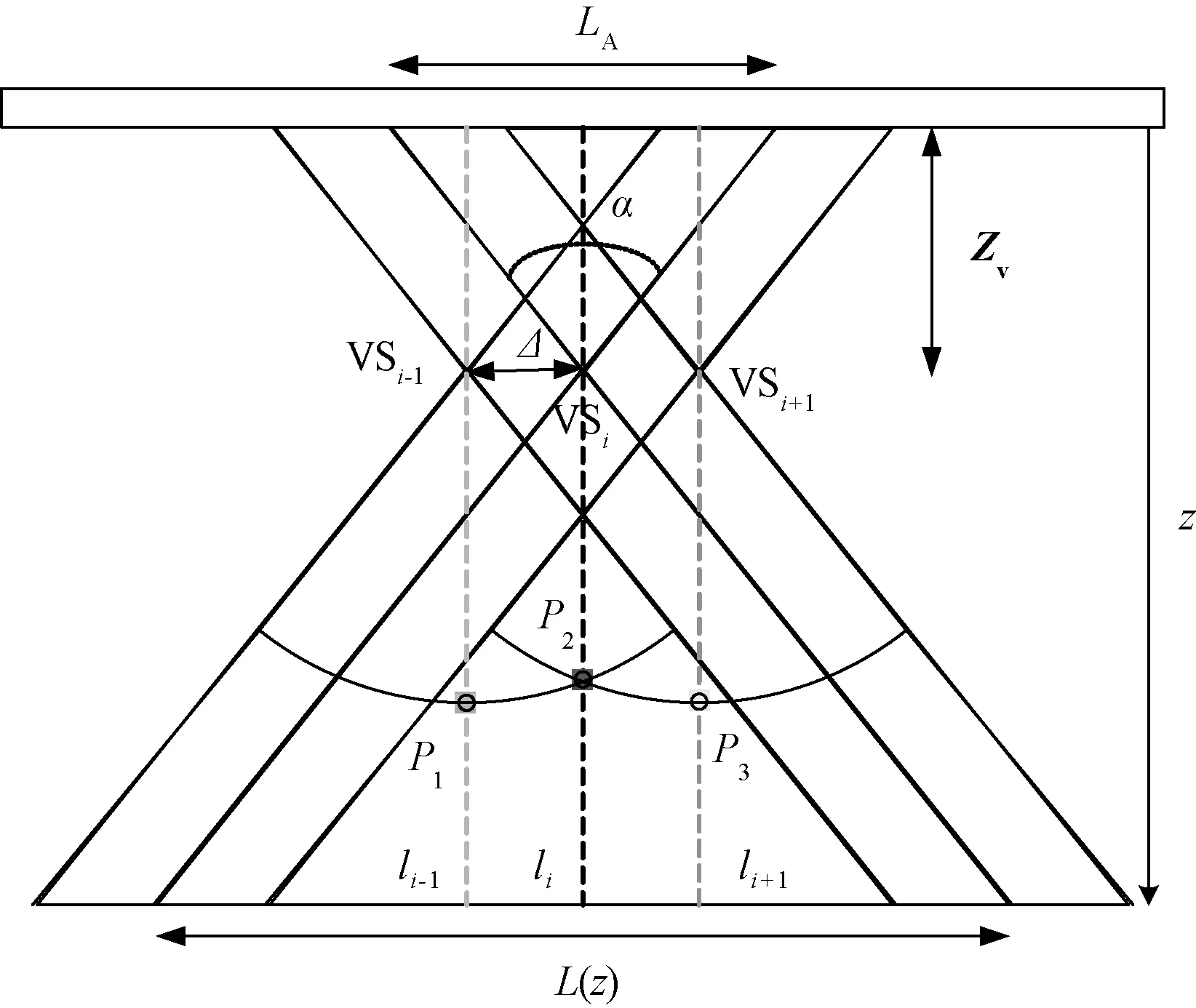
图1 合成孔径序列波束方法原理Fig.1 Model of SASB

1)第一阶段波束形成。采用传统的线性扫描方式，每次发射和接收采用单焦点，且发射与接收焦点相同。在成像扫描过程中，每次聚焦发射接收均可看作是一个虚拟阵元VSi发射了一定夹角的球面波，形成了一条扫描线li。多个虚拟阵元构成一个虚拟阵列。

2)第二阶段波束形成。在传统成像中，线li上的点P2只利用以VSi为发射焦点得到的发射声场来获得。实际上，其邻近扫描线(如li-1和li+1)上也包含P2点的信息。

例如，由li-1提取P2点信息，计算时延值，有

(1)

式中：c为声速，Zv为虚拟源深度，|P2VSi-1|)为P2点到线li-1上的虚拟源VSi-1的距离；“+”表示P2点深度大于Zv，“-”表示深度小于Zv。

由于P2点与P1点都在以VSi-1为圆心的弧上，所以式(1)的含义为P1点含有P2点的信息。

随着目标点与虚拟源距离的增加，更多扫描线包含目标点的信息，第二次波束形成使用到的虚拟源数目K也随之增多，实现了动态孔径，从而实现与深度无关的横向成像分辨率[13]。K可直接由图1的几何关系来计算，有

(2)

式中，α=2arctan(LA/(2Zv))为虚拟源的开角，L(z)为深度z处的声场宽度，Δ为虚拟源间距。

在依次对所有扫描li进行第二阶段波束形成来合成高分辨图像时，各图像点可计算为

(3)

式中，x为图像的横坐标，z为深度坐标，lk(td(k))表示第一阶段所得的扫描线lk上延时td(k)对应的值，w为加权函数，随深度z和扫描线的水平位置xk而改变。

式(3)的含义是将K(z)条扫描线上的对应值加权叠加，得到高分辨率的成像点。

1.2 运动对合成孔径序列波束形成方法的影响

对于成像目标静止的情况，上述合成孔径序列波束形成方法能够不增加硬件系统的复杂性，有效提高横向分辨率。仿真实验采用Field II[15]软件进行，其参数设置如表1所示。

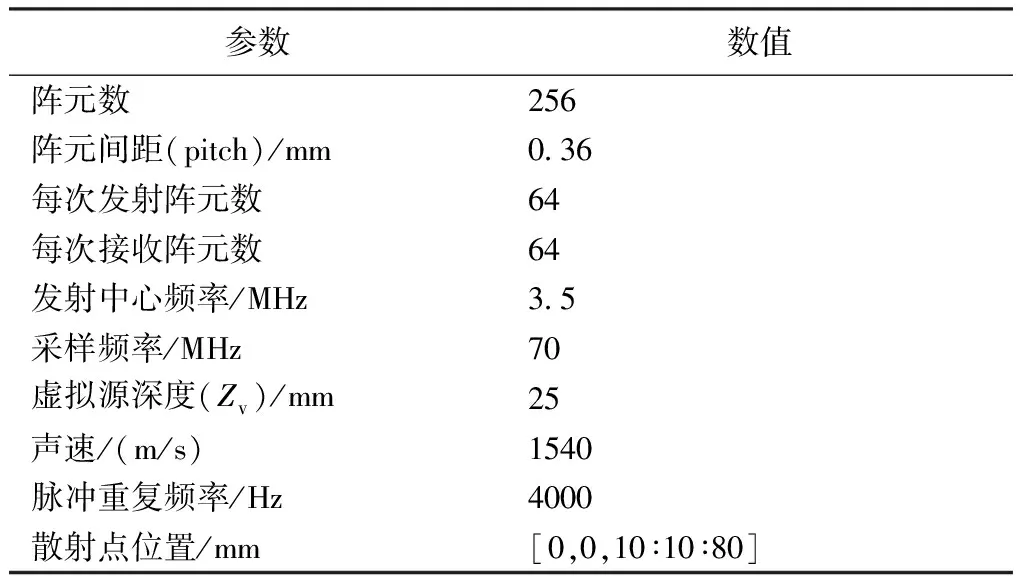
表1 仿真实验参数设置

如图2所示，在组织静止情况下，采用合成孔径序列波束形成方法，得到两个阶段波束形成。

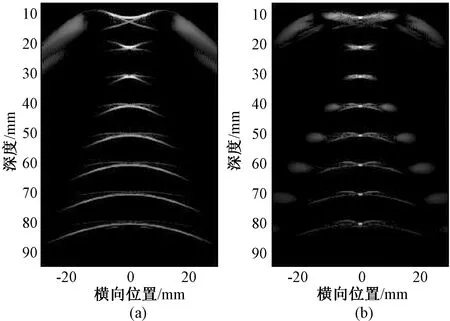
图2 静止情况下合成孔径序列波束形成(显示动态范围60 dB)。(a)第一阶段波束形成；(b)第二阶段波束形成Fig.2 Images of static points simulation(The dynamic range is 60 dB). (a)The first stage beamforming；(b)The second stage beamforming

对于被测组织存在运动的情况，以组织沿轴向向下以0.2 m/s的速度匀速运动为例，按照表1的参数进行仿真，采用合成孔径序列波束形成方法，得到两个阶段的波束形成，如图3所示。

由图3(a)可以看出，由于组织存在向下的轴向运动，第一阶段成像较静止情况(见图2(a))产生了变化。在此情况下，仍按照静止情况的采样点位置关系进行第二阶段波束形成，会造成成像点位置错误，如图3(b)所示。

图3 运动情况下合成孔径序列波束形成(显示动态范围60 dB)。(a)第一阶段波束形成；(b)第二阶段波束形成Fig.3 Images of points motion simulation (The dynamic range is 60 dB). (a)The first stage beamforming；(b)The second stage beamforming

1.3 运动补偿方法

为了解决运动对合成孔径序列波束形成方法造成的影响，笔者在本研究中提出一种运动补偿方法。

首先使用互相关方法进行运动估计。由于相邻两条扫描线的发射阵元不同，其相关性较差，所以不能直接采用第一阶段波束形成的相邻两条扫描线li与li+1做互相关来估计这两条扫描之间的运动。由于两条扫描线的物理位置非常接近，所以用同一位置连续两次发射间的运动来估计近似相邻两条扫描线间的运动。具体的数据获取和处理过程如图4所示，具体实现流程如下：

(4)

(5)

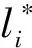
如果所有扫描线以第一条扫描线为基准进行补偿，即dcomp(1)=0，则第i条扫描线的补偿值为

(6)

为了提高运动估计精度，可以先对扫描线进行插值，也可以对时延估计结果进行插值[11]，即

(7)

则

(8)

采用式(8)进行运动补偿，得到补偿后的低分辨率扫描线cli。其中，Round()为四舍五入取整函数。

3)第二阶段波束形成。以运动补偿后得到的扫描线为输入，利用式(3)做波束形成，得到高分辨率扫描线，即

(9)

式中，w(xk，z)采用汉明窗。

图4 合成孔径序列波束形成运动补偿方法Fig.4 Illustration of SASB motion compensation method

1.4 仿真测试方法

为了验证所提出方法的有效性，用Field II软件进行了仿真实验，与表1不同或增加的仿真参数如表2所示。

表2 仿真实验参数设置

仿真中的阵元总数为128，每次发射和接收的阵元数都为64，具体成像过程为：

2)按照本文1.3节中描述的方法，以第一根扫描线为基准进行运动估计和补偿。

3)第二阶段波束形成，以运动补偿后得到的扫描线为输入，利用式(3)做波束形成，得到高分辨率扫描线cli(i=1,2,…,65)。

为了验证本方法对于点目标的运动补偿效果，

设空间有8个点，深度分别为10～80 mm，间隔为10 mm。用横向-6 dB宽度表征横向分辨率，用第一旁瓣高度表征对比度。由于发射和接收阵元数确定后，发射和接收焦点深度以及组织的轴向运动速度对本方法的成像效果影响较大，所以分别对焦点深度为25、35、45 mm和点目标静止及竖直向下运动速度为0.1、0.15、0.2 m/s共12种情况进行仿真实验。

为了验证本方法对于囊目标的运动补偿效果，在空间设置两个囊目标，深度分别为40和60 mm，半径都为4 mm，竖直向下运动，运动速度为0.2 m/s，焦点深度为25 mm。定义对比度分辨率[8]为

(10)

式中，CRref为参考图像的对比度分辨率，CRobj为测试图像的对比度分辨率。对比度分辨率CR[16]可定义为

(11)

式中，Ic为囊肿内的强度，Is为背景的强度。

文中取囊肿在图像中的横向对称位置为参考图像。

2 结果

2.1 点目标仿真结果

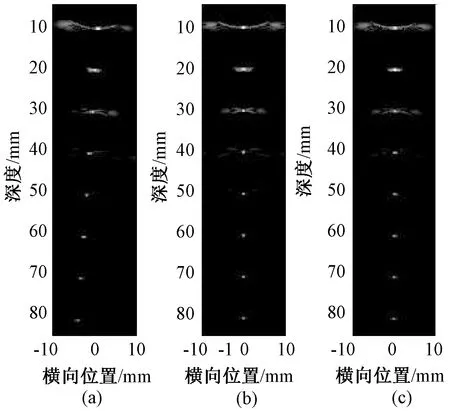
图5 点目标仿真结果。(a)未做运动补偿；(b)静止点目标；(c)做运动补偿Fig.5 Image results of point simulation. (a)Uncompensated；(b)Stationary points；(c)Compensated

图5为合成孔径序列波束形成方法对点目标的仿真结果，其中焦点深度为25 mm，运动速度为0.1 m/s，显示动态范围为40 dB；(a)为未做运动补偿的成像结果，(b)为静止情况下的成像结果，(c)为用本方法以第一条扫描线为基准做运动补偿后的成像结果。由图像可以看出，运动对于合成孔径序列波束形成方法的成像效果影响较严重，未做运动补偿的成像结果严重失真。所提出的运动补偿方法可以有效避免运动对合成孔径序列波束形成方法成像效果的影响，成像结果与静止点目标相似。

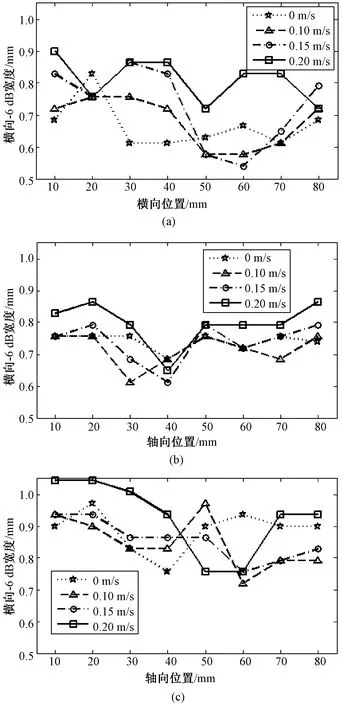
图6 不同焦点深度情况下的横向-6 dB宽度。(a)Zv=25 mm；(b)Zv=35 mm；(c)Zv=45 mmFig.6 Lateral width at -6 dB for different focus depth. (a)Zv=25 mm；(b)Zv=35 mm；(c)Zv=45 mm

图6为不同焦点深度点目标静止和轴向运动速度分别为0.1、0.15、0.2 m/s时运动补偿后的横向-6 dB宽度，其中图6(a)～(c)对应的焦点深度分别为25、35、45 mm。可以看出，当运动速度为0.2 m/s时，多数点目标对应的横向-6 dB宽度都有所增加，而运动速度0.1和0.15 m/s时的结果与静止时的情况类似。

进一步地，表3给出了焦点深度为25 mm时不同运动速度下8个散射点横向-6 dB宽度均值，以及相对于静止情况的增加百分比。当运动速度为0.1 m/s时，横向-6 dB宽度均值仅增加2.03%，随着速度加大，横向-6 dB宽度均值增加幅度增大。

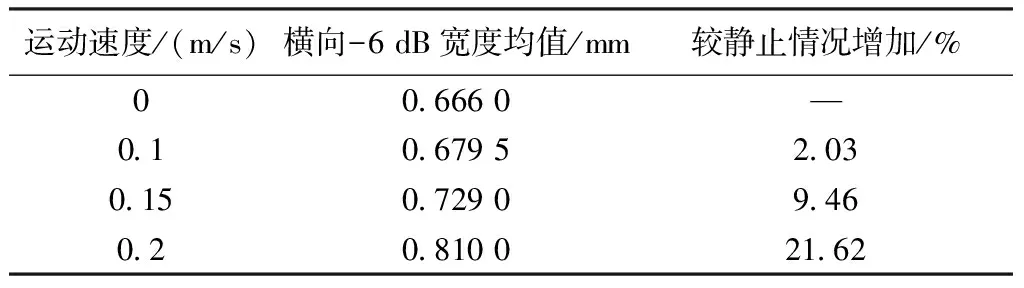
表3 Zv=25 mm时8个散射点横向-6 dB宽度均值

图7为不同焦点深度点目标静止和轴向运动速度分别为0.1、0.15、0.2 m/s时运动补偿后的第一旁瓣高度，其中图7(a)～(c)对应的焦点深度分别为25、35、45 mm。可以看出，运动速度为0.1 m/s时，补偿后的第一旁边高度与静止情况时的类似，随着速度的增加，第一旁瓣高度有所升高，尤其是运动速度达到0.2 m/s时升高比较明显。

图7 不同焦点深度情况下的第一旁瓣高度。(a)Zv=25 mm；(b)Zv=35 mm；(c)Zv=45 mmFig.7 Height of the first sideband for different focus depth. (a)Zv=25 mm；(b)Zv=35 mm；(c)Zv=45 mm

表4给出了焦点深度为35 mm时8个散射点第一旁瓣高度均值的增加情况。其中，速度为0.1 m/s时补偿后的第一旁瓣高度均值较静止情况增加2.7 dB，速度为0.15 m/s时增加5.4 dB，速度为0.2 m/s时增加10.3 dB。

表4 焦点深度为35 mm时8个散射点第一旁瓣高度均值

2.2 囊目标仿真结果

图8为合成孔径序列波束形成方法对囊目标的仿真结果，显示动态范围为40 dB，其中(a)为未做运动补偿的成像结果，(b)为静止情况下的成像结果，(c)为用本方法以第一条扫描线为基准做运动补偿后的成像结果。由图像可以看出，运动对于合成孔径序列波束形成方法的影响较大，未做运动补偿的成像结果严重失真，深处的囊目标有一部分已经不在成像区域内。所提出的运动补偿方法对于囊目标可以有效避免运动对合成孔径序列波束形成方法成像效果的影响，成像结果与静止囊目标相似。

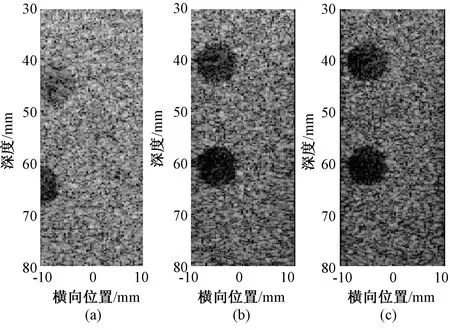
图8 囊目标仿真结果。(a)未做运动补偿；(b)静止囊目标；(c)做运动补偿Fig.8 Image results of cysts motion simulation. (a)Uncompensated；(b)Stationary cysts；(c) Compensated

对于上述设定的囊目标，根据式(10)计算运动补偿后的图像(见图8(c))较囊肿静止情况的图像(见图8(b))的对比度分辨率仅降低8.53%。

3 讨论和结论

由于不需要存储和传输大量单阵元接收的RF线数据，合成孔径序列波束方法的实现复杂度较合成发射孔径方法的实现复杂度大大降低。合成孔径成像的前提是假设成像目标静止不动，对于传统的合成发射孔径方法，成像目标的运动会造成低分辨率图像间产生某种错位，从而造成高分辨率图像对比度的严重下降[10]。而从本文对组织运动对合成孔径序列波束方法影响的分析中可以看出(见图3)，成像目标运动最主要的影响是会造成最终成像结果中目标点的位置错误。在采用所提出的运动估计和补偿方法后，从点目标和囊目标的仿真结果看(见图5、8)，运动造成的位置错误问题都得到了解决。但是，由于采样率等因素对运动估计和补偿精度的限制，比较静止情况，从点目标的仿真结果看，运动补偿后的成像结果的横向分辨率和对比度均有下降，运动速度越快，下降越明显：当运动速度为0.1 m/s时，横向-6 dB宽度均值和第一旁瓣高度均值较静止情况分别增加2.03%和2.7 dB；而运动速度为0.2 m/s时，则分别增加21.62%和10.3 dB。从囊目标的仿真结果看，速度为0.2 m/s时，运动补偿后的成像结果的对比度分辨率下降8.53%。值得注意的是，影响运动补偿后成像效果实际是两次脉冲发射间组织的位移，所以与彩色血流成像类似，可以依据具体情况通过调整系统的脉冲重复频率，使运动补偿保持较好的效果。此外，提高采样率或者信号处理过程中插值的倍数，可以降低运动估计和补偿误差，从而进一步提高存在组织运动情况下合成孔径序列波束形成方法的成像分辨率和对比度。

为了获得用于运动估计的数据，本研究用运动补偿方法在同一位置连续发射接收2次，这样做的优点：一是用相同阵元获取的数据做运动估计，相关性高、鲁棒性强，否则速度的快慢变化容易引起数据相关性差而造成估计失败；二是可实现性强，硬件修改小或者不用修改，有利于现有设备的技术改造；三是成像的效果较好，可以有效地避免组织运动造成的成像点位置错误问题。但此方法也存在一些缺点：一是数据计算量增大，波束形成计算量是不补偿的2倍，另外还增加了互相关算法的计算量,但随着硬件水平的增加和算法的优化，计算量大的问题将会得到解决；二是由于要在每个位置发射2次，成像的帧频率降低1倍，因此限制了算法在高帧频场景的应用。

本研究首先分析了组织运动对合成孔径序列波束形成方法成像效果的影响，发现组织的轴向运动造成成像点的位置错误；然后针对这一问题提出了一种合成孔径序列波束形成方法的运动补偿算法，用在第一阶段波束形成过程中，同一位置连续发射接收2次以获取用于运动估计的数据。仿真实验结果显示：当组织运动速度不大时，如0.1 m/s，所提出的运动补偿方法对于运动点目标可以得到与静止点目标相似的横向分辨率；在对运动速度为0.2 m/s的囊目标运动补偿后，图像的对比度分辨率较静止情况仅降低8.53%，说明该运动补偿方法有效。

下一步研究的重点，是如何在不降低成像帧频的前提下做有效的运动补偿。此外，笔者提出的运动补偿方法主要针对组织的轴向运动，没有考虑组织的横向运动。仔细分析组织横向运动对合成孔径序列波束形成方法成像效果的影响，并有针对性地研究横向运动补偿方法，也是下一步研究的方向。

[1] 林轶翰，陈思平. 医学超声影像技术及展望 [J]. 医疗装备, 2006, 19(6):13-15.

[2] Fort JR, Landmeier PC, Morgan DJ,etal. Synthetic aperture ultrasound imaging system [P]. U.S. Patent: 5465722. 1995-11-14.

[3] Burckhardt CB, Grandchamp PA, Hoffmann H. An experimental 2 MHz synthetic aperture sonar system intended for medical use [J]. IEEE Transactions on Sonics and Ultrasonics, 1974, 21(1): 1-6.

[4] Nagai K. A new synthetic-aperture focusing method for ultrasonic B-scan imaging by the Fourier transform [J]. IEEE Transactions on Sonics and Ultrasonics, 1985, 32(4): 531-536.

[5] Nikolov SI. Synthetic aperture tissue and flow ultrasound imaging [D]. Lyngby: Technical University of Denmark, 2001.

[6] Jensen JA, Nikolov SI, Gammelmark KL,etal. Synthetic aperture ultrasound imaging [J]. Ultrasonics, 2006, 44: e5-e15.

[7] Karaman M, Li PC, O’Donnell M. Synthetic aperture imaging for small scale systems [J]. IEEE Trans Ultrason Ferroelec Freq Contr, 1995, 42(3): 429-442.

[8] Gammelmark KL, Jensen JA. Multielement synthetic transmit aperture imaging using temporal encoding [J]. IEEE Trans Med Imaging, 2003, 22(4): 552-563.

[9] Gammelmark KL, Jensen JA. Duplex synthetic aperture imaging with tissue motion compensation [C] //Yuhas DE, eds. 2003 IEEE Symposium on Ultrasonics (Volume 2 ). Hawaii: IEEE, 2003: 1569-1573.

[10] Yiu BYS, Tsang IKH, Yu ACH. A modified synthetic aperture imaging approach with axial motion compensation [C] // Waters KR, eds. Proceedings of IUS 2008. Beijing: IEEE, 2008: 1254-1257.

[11] Lockwood GR, Talman JR, Brunke SS. Real-time 3-D ultrasound imaging using sparse synthetic aperture beamforming [J]. IEEE Trans Ultrason Ferroelec Freq Contr, 1998, 45: 980-988.

[12] Hazard CR, Lockwood GR. Theoretical assessment of a synthetic aperture beamformer for real-time 3-D imaging [J]. IEEE Trans Ultrason Ferroelec Freq Contr, 1999, 46: 972-980.

[13] Kortbek J, Jensen JA, Gammelmark KL. Sequential beamforming for synthetic aperture imaging [J]. Ultrasonics, 2013, 53(1): 1-16.

[14] Trahey GE, Nock LP. Synthetic receive aperture imaging with phase correction for motion and for tissue inhomogeneities. II. Effects of and correction for motion [J]. IEEE Trans Ultrason Ferroelec Freq Contr, 1992, 39(4): 496-501.

[15] Angelsen BAJ. A theoretical study of the scattering of ultrasound from blood [J]. IEEE Trans Biomed Eng, 1980, BME-27: 61-67.

[16] Foster SG, Embree PM, O’Brien WD. Flow velocity profile via time-domain correlation: Error analysis and computer simulation [J]. IEEE Trans Ultrason Ferroelec Freq Contr, 1990, 37(3): 164-175.

An Axial Motion Compensation Method for Synthetic Aperture Sequential Beamforming

Meng Xiaohui Li Hua*Wang Junlin

(InstituteofAcoustics,ChineseAcademyofSciences,Beijing100190,China)

Synthetic aperture sequential beamforming (SASB) is a two-stage beamforming procedure, which can be applied to B-mode imaging with an implementation of low complexity compared to the traditional synthetic transmit aperture (STA) imaging. However, like the STA imaging, the SASB is susceptible to motion artifacts due to the summation of a number of RF-data created at different time instances. In this paper, a tissue motion estimation and compensation method was proposed. First, the inter-firing motion was estimated by cross-correlating with extra firings. At last, the second stage beamformer created a set of high resolution image points by combining information from multiple first stage focused scan lines. Field II simulation results showed that the motion compensation method proposed in this paper exhibited enhanced ability to correct location of moving tissue. When the points were moving at 0.1 m/s, the average lateral resolution after motion compensation was only reduced by 2.03% comparing to the static case, and contrast reduction was 2.7 dB. Moreover, when cysts were moving at 0.2 m/s, the contrast resolution of image after motion compensation was only reduced by 8.53% comparing to the static case.

synthetic aperture; synthetic aperture sequential beamforming; motion compensation

10.3969/j.issn.0258-8021. 2015. 05.006

2014-07-14， 录用日期:2015-07-06

国家自然科学基金(11204346)；中国科学院声学研究所所长择优基金(Y454221341)；中国科学院声学研究所创新前瞻项目(Y154211341)

R445.1

A

0258-8021(2015) 05-0558-08

*通信作者(Corresponding author)， E-mail: leehwa@mail.ioa.ac.cn