履带式两栖车辆绕流场的数值计算

（解放军理工大学野战工程学院，江苏 南京 210007）

履带式两栖车辆航行时的水动力特性与轮式两栖车辆有一定差异，开展履带式两栖车辆的绕流场及水动力特性研究，将对提高履带式两栖车辆的水上性能有很大意义[1]。根据数值分析结果，可以实现对车体的外形进行优化设计，为今后研制具有更好水上性能，能够适应更加复杂海况的新型两栖车辆，提供一定的理论依据。

近年来，随着计算机性能的提升和数值模拟方法的不断改进，使得计算流体力学(CFD)的应用范围不断拓展。借鉴船舶的流场数值模拟方法，利用CFD软件，对两栖车辆的绕流场进行数值分析，是更为经济、快捷、高效的方法[2]。

1 数学模型

1.1 湍流模型的控制方程

连续方程[3]：

△·u=0

动量方程：

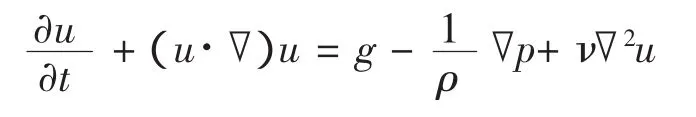
1.2 边界条件设置

计算区域的边界条件包括：壁面、速度进口、出口边界、对称面、交界面。具体设置情况如下：

（1）壁面：将装备车体表面和远场壁面设置为无滑移边界条件。

（2）速度进口：按照车辆航速确定，湍动能和湍流耗散率参照经验公式给出。

（3）出口边界：装备航行过后，其后部的流动可认为是完全发展的，适用出口边界条件。

（4）对称面：将车体的中心面定义为对称面边界条件。

（5）交界面：由于近车体流场与外部流场所划分的网格类型不同，要实现结构化网格与非结构化网格间的相互关联，就要将两种网格的重合面定义为为交界面边界条件。

2 数值计算

2.1 计算模型

两栖车辆车体表面线型复杂，主要研究其水中航行时的流场特性，因此计算模型需要有所简化，模型的基本尺寸来源于实装，如图1所示。

图1简化的车体几何模型示意图

车体总长7.67 m，宽3.1 m。车体模型的长宽比L/B＝2.48，影响其快速性和航向稳定性；车宽吃水比B/T=1.94，影响其抗横摇稳性；车高吃水比H/T=1.3，一定程度影响其抗沉性和装载能力。

2.2 网格划分

网格划分的策略，需要根据工程问题的具体情况来制定。不同的网格划分策略，对生成的网格质量影响很大。而网格质量的好坏，直接关系到数值计算的精确性、收敛性和时效性。因此，应根据两栖车辆的绕流场具体情况，进行网格划分。如图2所示。

图2 计算区域划分

在近车体流场区域采用非结构化网格，并在车体近壁范围内使用边界层过渡网格，外围流场区域采用结构化网格，并对车体和自由液面附近的网格进行加密处理。如图3所示。

图3 车体表面网格

2.3 离散格式

本文控制方程的扩散项采用中心差分格式离散，对流项采用如下格式离散：梯度设置为最小二乘法，对于压力方程采用体积力加权格式，动量方程、湍动能方程均采用二阶迎风格式。对于瞬态问题，压力隐式算子分割算法（PISO）有明显的优势，故压力速度耦合方式采用PISO算法。取时间步长为0.01 s，需要求解的时间步数设定为2 000步，每个时间步长内的最大迭代次数设为20。为了保证湍流计算的收敛性和稳定性，欠松弛因子分别取为0.6、0.4、0.8、0.4、0.6、0.6、0.8.

3 数值模拟与分析

3.1 数值方法验证

应用FLUENT软件，对两栖车辆的车体绕流场进行数值模拟，得到两种湍流模型下的阻力计算值，如表1所示。根据计算数据绘制出阻力随速度变化曲线，并对比试验数据拟合曲线，如图4所示。数值模拟结果总体上与试验结果相吻合，略小于试验值。可以看出两种模型所计算出的阻力曲线的变化趋势，与试验值的变化趋势相一致。两种湍流模型都能比较好地计算车体的航行阻力，相比之下，RNG模型的计算结果与试验值更接近，误差更小。所以RNG湍流模型，更适合两栖车辆的阻力计算。误差主要是由于在数值模拟中，模型的精度不高而产生的。

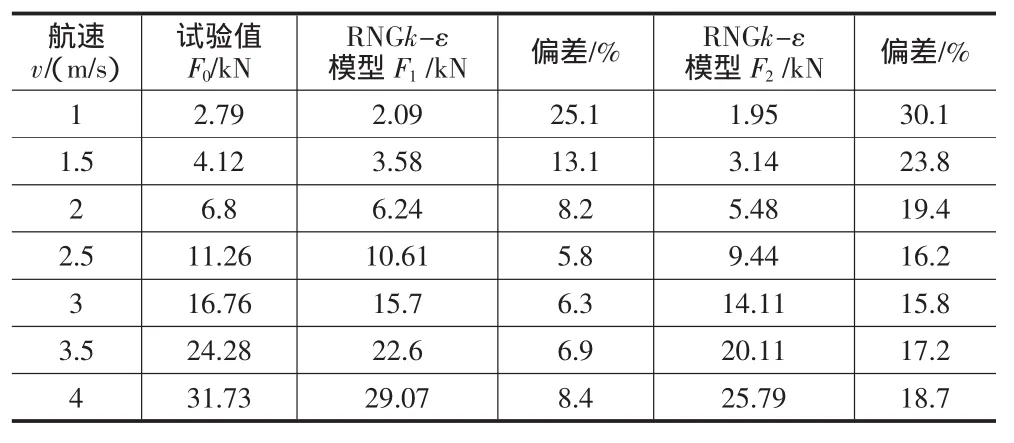
表1两种模型计算结果与试验结果比较

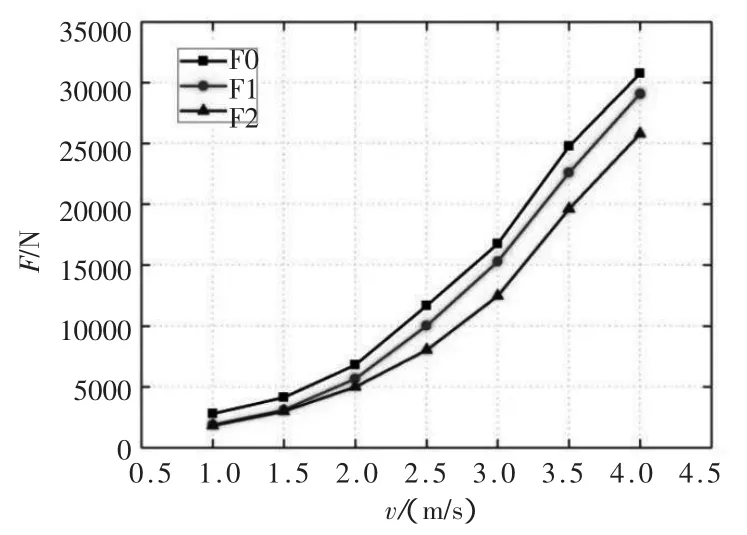
图4总阻力的模拟值与试验值

3.2 计算结果分析

通过数值模拟计算，得到了两栖车辆水中航行时的流场特性参数。可以根据需要对其进行相关水动力特性分析。图5为车体在航速v=3m/s的情况下履带前部和后部的速度矢量图。由于车体形状在此处的急剧变化，导致此处的流体运动发生了分离，并且产生了尺度较大的涡，降低了通过该处的水流速度，使得该区域压力降低，如图6动压分布所示。在车体周围形成压力差，产生较大的压差阻力。

图5 履带轮附近的速度矢量图

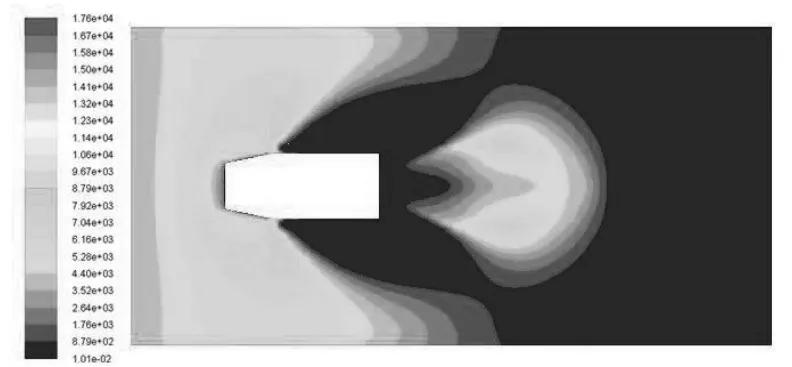
图6 动压分布云图

图7反映了车辆在4m/s航速下的兴波云图。从云图中可以看出，车体首部有一较大的波峰，在车体履带前端两侧形成波谷；车体后部由于履带的影响，向两侧扩散形成较小波峰，车体正后方处于波谷。其总体自由液面的波形刻画与车体表面动压分布相符，也接近车体航行的实际情况。从上可证明兴波阻力的大小与车体形状密切相关，对车体外形局部进行合理优化，可以提高其水上动力性能，达到减阻增速的目的。

图7 航速4m/s的兴波云图

4 结束语

利用CFD计算流体力学的方法，对两栖车辆的绕流场进行数值模拟，获得其水上航行时主要的流场特性参数。模拟计算中考虑了自由液面的影响，通过VOF方法对兴波自由液面进行了追踪。采用两种湍流模型分别对装备车体绕流场进行了数值模拟，数值模拟计算出的阻力值与试验值基本吻合，比较总阻力的计算值与试验值，确定了RNG模型是更为适合两栖车辆绕流场数值模拟的湍流模型。同时，分析了车体外形对阻力的影响，找到影响其航行阻力的关键因素，为今后更高性能的两栖车辆的研制提供了参考。

[1]洪 津，高 博，王 璞，等.两栖工程作业车的发展研究[J].化学工程与装备，2010，(8)：159-160.

[2]高富东，姜乐华，潘存云．基于计算流体动力学的两栖车辆水动力特性数值计算[J]．机械工程学报，2009，(5)：134-139．

[3]杨楚泉．水陆两栖车辆原理与设计[M].北京：国防工业出版社，2003.

[4]居乃鵕．两栖车辆水动力学分析与仿真[M]．北京：兵器工业出版社，2005.

[5]赵建民，朱 军，焦志勇，等.两栖车辆水陆运动模型[J].四川兵工学报，2011，(5)：11-15.

[6]韩占忠，王国玉，闫为革.两栖车辆航行粘性阻力数值分析[J].车辆与动力技术，2003，(2)：6-10.