基于简单占空比调节的异步电机直接转矩控制
2015-02-19李政学张永昌李正熙班晓娟杨海涛
李政学 张永昌 李正熙 班晓娟 杨海涛
(1.北京科技大学计算机与通信工程学院 北京 100083
2.北京市电力电子与电气传动工程研究中心(北方工业大学) 北京 100144)
1 引言
迄今为止,磁场定向控制(Field Oriented Control,FOC)和直接转矩控制(Direct Torque Control,DTC)已经成为在高性能交流调速领域中两种最为常用的方法[1]。相比于磁场定向控制,直接转矩控制在静止的定子坐标系中进行计算,无需旋转坐标变换,电流调节器和脉宽调制模块[1-4];它使用两个滞环比较器和一个开关表,根据磁链和转矩的瞬时误差选择使定子磁链和转矩向各自的给定值变化的电压矢量,具有非常简单的结构和快速的动态转矩响应能力[5]。另外,DTC 在运算中使用的电机参数非常少,大大减小了电机参数波动对控制性能的影响。
传统DTC 的一个显著缺点是输出转矩脉动大、开关频率不恒定。空间矢量调制(SVM)技术可以有效地解决这个问题[6,7]。SVM 技术的基本思想是,在每一个控制周期中,通过计算得到一个能够恰好补偿当前定子磁链和转矩误差的电压矢量。该电压矢量可以用两个相邻的有效电压矢量和零电压矢量合成得到。这种基于SVM 技术的DTC 算法可以极大地减小输出转矩的脉动,同时获得了恒定的开关频率。但是,它的计算量非常大,而且使用了更多的电机参数。虽然控制性能有所提高,却丧失了DTC 控制结构简单的优点。
另一种减小转矩脉动的方法是采用占空比控制(duty ratio control)技术,该方法与SVM 技术相比复杂性有所降低。它的基本思想是,在每个采样周期中,有效电压矢量只作用一部分时间,剩余时间选择零电压矢量。针对如何确定每个采样周期中有效电压矢量作用时间的问题,提出了多种方法。其中最有代表性的三种方法是[8-12]:①无差拍控制;②平均转矩控制;③转矩脉动最小控制。另外,还可以采用模糊逻辑自适应方法[13-15]来获得占空比。这些方法获得了很好的控制性能,但是通常计算量较大,并且严重依赖电机参数。
最近,模型预测控制(MPC)在电机高性能控制中得到了广泛研究和关注[16-19]。这种方法与DTC的相似之处是都直接选择最终电压矢量,但 MPC选择矢量时是依赖于系统模型和评价函数,而非DTC 中的矢量表。比如文献[16]通过对每个可能开关状态代价函数的评估,选择最能满足性能要求的电压矢量输出。文献[17]提出一个三电平逆变器馈电的DTC 方案,它使用多步预测取得开关频率的减小,同时控制转矩、磁链和中点电位在各自的滞环带内。MPC 相比DTC 有更好的稳态性能,但是计算量大,对模型和参数的精度要求较高。
DTC 需要对定子磁链进行估计,本文采用基于全阶观测器的方法估计磁链[20-22],只需两路直流母线电压和两路电机电流信号,可以在全速域范围内准确地观测磁链,并成功地将观测得到的磁链用于闭环DTC 中。
目前针对异步电机而言,还没有文献对各种占空比控制方法进行过比较研究。本文首先在详细比较三种典型占空比确定方法性能的基础上,提出一种简单而非常有效的占空比确定方法。该方法保持了传统DTC 的结构简单性,在占空比确定中考虑对转矩和磁链误差的同时优化,获得了同时减小转矩和磁链脉动的良好性能。为了进一步改善系统性能,使用基于全阶观测器的方法观测定子磁链,可以在全速域范围内准确的观测磁链。仿真和实验结果证明了本文所提方法的可行性和在减小转矩和磁链脉动方面的有效性。
2 异步电机的数学模型
2.1 电机方程
在d-q 静止坐标系中,利用空间矢量表示的电机方程为

式中 ψs,ψr——定子和转子的磁链矢量;
us——定子电压矢量;
is,ir——定子和转子电流矢量;
ωr——转子的电角速度;
Ls,Lr——定子和转子的自感;
Lm——互感;
Rs,Rr——定子和转子的电阻。
由式(1)~式(4)得到使用定子和转子磁链矢量作为状态变量的异步电机状态方程为

电磁转矩可以使用定子和转子磁链矢量的叉积表示为

式中 np——电机的极对数;
2.2 电压矢量对转矩和磁链的影响
标准的两电平电压源逆变器(VSI)的输出只有8 种电压矢量,包括6 个有效电压矢量(V1~V6)和2 个零电压矢量(V0,V7)。根据有效电压矢量的位置,坐标平面分为6 个扇区,如图1 所示。
对于电压源逆变器馈电的DTC 系统,电压矢量是唯一的可控制的输入变量,因此希望解析推导出转矩和磁链变化量与电压矢量之间的关系。

图1 8 个电压矢量和6 个扇区 Fig.1 8 voltage vectors and 6 sectors
由式(6)求解转矩对于时间t 的微分可得
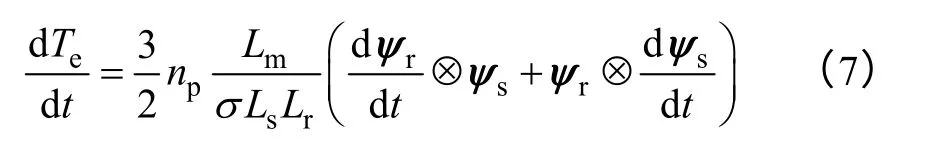
将式(5)代入式(7),经过推导最终得到转矩微分为

式中,⊙表示矢量点积。
从式(8)可以看出转矩微分由3 部分构成:第一部分ΔTe1与转矩成反比;第二部分ΔTe2与转速相关;最后一部分ΔTe3反映了定子电压矢量对转矩的影响。
当选择零电压矢量时,转矩微分变为

从式(9)中可以看出,零电压矢量一般导致负的转矩变化。
如果时间间隔非常短,并且在忽略定子电阻压降的情况下,式(1)可以改写为

由式(10)可以看出,在一个极短的时间段内,作用某一电压矢量后所产生的定子磁链矢量的改变量,与该电压矢量具有相同的方向;如果能够合理控制作用于电机的合成电压矢量us的大小,就能控制磁链的变化量,使磁链的误差控制在磁链滞环带宽内,这也正是传统DTC 的基本原理。
在传统DTC 中,滞环比较器不区分转矩和磁链误差的大小,从开关表中选出的电压矢量将作用于整个采样周期。在转矩误差较小的周期中,转矩很快达到参考值,之后继续增大或减小,导致了较大的转矩脉动。占空比控制技术的应用可以解决这个问题,在占空比控制中,所选的有效电压矢量只在该采样周期中作用一部分时间,而剩余的时间选择零电压矢量。有效电压矢量作用时间占采样周期时间的比率称作占空比d,其取值范围是0~1。
3 经典的占空比确定方法
3.1 基本原理
由(8)式看出,通过调整电压矢量us的幅值和作用时间可以改变转矩的大小。电压矢量的幅值是由直流母线电压决定,通常是固定的,而us的作用时间可以由零变化到整个采样周期,这等效于改变了电压矢量的长度。从式(9)看出,零电压矢量只能减小转矩,而合适的有效电压矢量能增大转矩,因此,在一个采样周期中同时使用零电压矢量和有效电压矢量可以减小转矩脉动。关键问题是如何决定这两个电压矢量的作用时间,或者说确定有效电压矢量的占空比。
3.2 经典占空比确定方法
三种经典占空比确定方法如图2 所示。


图2 三种经典占空比确定方法原理 Fig.2 Basic principle of the three classical duty ratio determination methods
方法1 期望瞬时电磁转矩在该采样周期末等于参考值,如式(11)所示,称之无差拍控制[8-10]。

现有文献[8,9]致力于磁链和转矩同时无差拍控制,为此需要求解一个二次方程式,其求解过程和结果表达式都相对复杂,而且对电机参数依赖性较强。为了减低算法复杂性,本文仅考虑转矩无差拍控制。
方法2 致力于使整个采样周期的平均电磁转矩等于参考值,如式(12)所示,也叫直接平均转矩控制[11]。

方法3 是使转矩脉动的方均根值(RMS)在一个采样周期中最小[12],表达式为
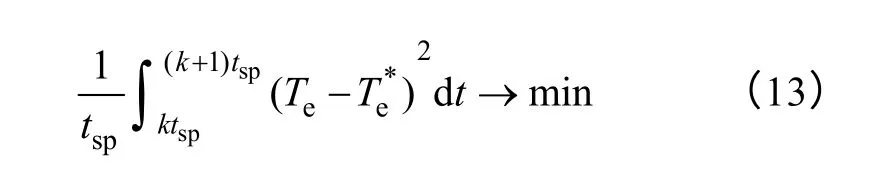
在一个很小的采样周期tsp内,因为磁链和转速的变化相对很慢,可以假设由式(8)和式(9)计算出的有效电压矢量的上升斜率f1和零电压矢量的下降斜率f2为常数。在这种假设条件下,通过求解式(11)~式(13)可得三种经典占空比确定方法中有效电压矢量的作用时间为


式中 T0——第k 个采样时刻的初始转矩;
d1,d2,d3——方法1、2、3 中有效电压矢量的占空比。
4 基于新占空比控制的DTC 方法
4.1 现有占空比方法的比较
从式(14)~式(16)所示的三种占空比确定方法表达式可以看出,虽然它们具有不同的形式,然而,有文献报道称与传统DTC 相比都获得了更好的性能。除了解析方法,还有模糊逻辑自适应方法[13-15],文献[13-15]中也报道说相比于传统 DTC转矩脉动明显减小。这些方法都启示如何获得确定占空比的方法并不重要,最重要的是必须使用零电压矢量,因此有可能采用更为简单的占空比控制方法来提高DTC 的性能。
4.2 新占空比方法原理
经典占空比确定方法如式(14)~式(16)所示,计算复杂并且对电机参数依赖大。其中,表达式(15)非常复杂,甚至需要计算开平方项。而式(14)和式(16)则比较相似,区别仅在分子和分母中第一项的系数。由这些不同占空比方法在表达式上的差异性启发可以做出更大胆的假设,即令式(14)~式(16)中的分母为常数,从而消除对电机参数的依赖性。换句话说,可以近似认为这是几种不同占空比方法的“混合”。由于使用零电压矢量可以减小转矩脉动,而对于占空比的确定方法似乎还没有统一的要求。本文在大量仿真和实验研究的基础上,采用定量与定性相结合的方法,对现有基于模型的占空比方法进行深度解析,提出一个简单易实现并且对参数变化鲁棒性强的新占空比确定方法,考虑了对转矩和磁链误差的同时优化。该新型占空比确定方法的原理如下。
在给出新的占空比确定方法之前,先来分析一下式(14)的占空比确定方法,重写为
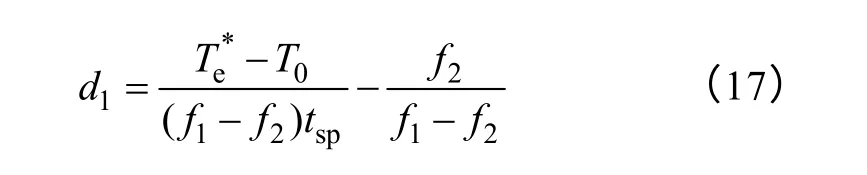
由式(17)可知,第一项正比于转矩误差,第二项正比于转矩的下降斜率f2。为了消除参数依赖性,不妨假定分母(f1-f2)tsp是常数,然而,式(17)中与f2相关的第二项仍然很复杂,正如式(9)所示,并且仍依赖电机参数。注意到转矩的下降斜率f2是由零电压矢量引起的,而零矢量一般会导致定子磁链幅值的降低,为此可以认为第二项与磁链误差成正比。考虑占空比的非负性,最终得到一种新型占空比确定方法,具体表达式为

式中 Te*,ψs*——转矩和定子磁链的参考值;
ψ0——第k 个采样时刻的定子磁链值;
CT,CF——正的常数。
通过使用固定的常数CT和CF,希望新占空比确定方法受到转矩斜率计算的影响更小。对于 CT和CF的调制应综合考虑转矩动态响应和稳态性能的影响,在进行大量仿真和实验研究的基础上发现,半额定的转矩值和恒定的定子磁链值效果比较理想。一旦调整好,CT和CF便是两个固定的常数。进一步研究发现,常数CT和CF的选择对系统性能的影响也不是很大。
需要指出的是,由于新占空比方法仅改变所选有效电压矢量的作用时间,而该有效电压矢量来自传统的DTC 矢量表。极端情况下占空比为1,此时则蜕化为普通的矢量表DTC。而在其他情况下,即使是在稳态运行时,磁链和转矩的瞬时误差也不大可能同时为0,式(18)采取的两个绝对值运算符保证了占空比大于0。因此,系统的稳定性不受影响。这也解释了为什么存在不同的占空比确定方法。它们的区别仅在于稳态脉动有所不同,但都可以保证系统的稳定性。
4.3 新占空比方法分析
与之前的占空比控制方法相比,简单性是本方法的第一个优点,可以看出式(18)比式(14)~式(16)更简单。第二个优点是对电机参数的变化鲁棒性更强。对于先前方法式(14)~式(16),由式(8)和式(9)计算的转矩斜率被用来确定占空比,它需要知道定子电阻、定子电感、转子电感和定转子互感等信息。而本文所提的新型占空比控制方法不需要额外的电机参数,因此受到电机参数变化的影响更小。
5 定子磁链估计
在DTC 中通常使用电压模型估计定子磁链,在低速时定子电压值较小,若定子电阻值不准确,定子电阻压降的偏差对积分结果的影响会增大。本文使用基于全阶观测器的方法估计定子磁链,可以在全速域范围内准确的观测磁链。
由式(1)~式(4)式得到使用定子电流矢量和定子磁链矢量为状态变量的异步电机模型为

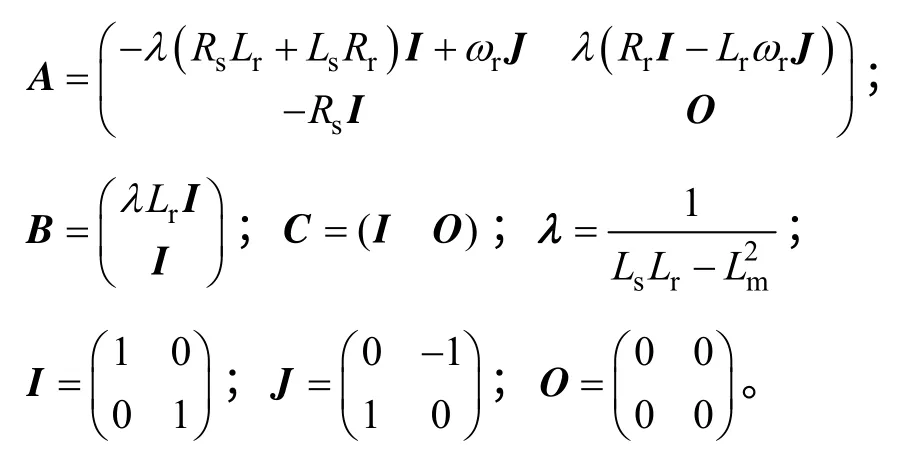
根据式(19)可以构造出异步电机的全阶观测器模型
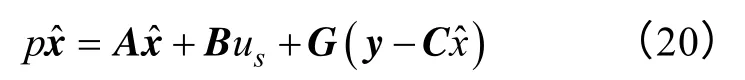
由于电机是稳定的物理系统,因此通常选择G使得观测器的极点正比于电机的极点[20,21],以保证观测器的稳定收敛,且一般k>1 以保证观测器的误差收敛速度。需要注意的是,观测器极点与电机极点的比值k 越大则观测器收敛速度越快,但相应的抗干扰能力下降,因此k 值的选择一般是快速性和抗干扰性的折衷。增益矩阵G 的一般形式为

本文采用文献[20]的方法,解析推导得到矩阵G 各个元素的表达式为

6 各种占空比确定方法的仿真比较
到目前为止针对异步电机还没有文献对各种占空比确定方法进行过比较研究,为此本文首先在Matlab/Simulink 中对已有经典方法和本文所提新方法进行仿真比较研究,以考察所提新占空比确定方法的性能。控制系统在1 050r/min 运行,采样频率为10kHz,系统的外环使用PI 速度控制器产生转矩参考值。转矩和磁链滞环比较器的宽度均设为零,其输出仅表明转矩和磁链误差的正负。基于新占空比控制的DTC 控制系统框图如图3 所示,异步电机和控制系统参数见下表。
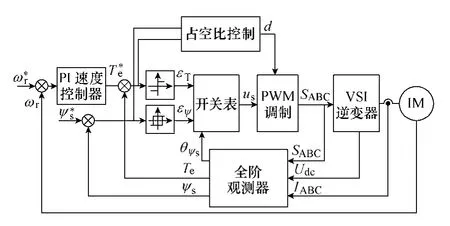
图3 新的基于占空比控制的DTC 控制系统框图 Fig.3 Basic block diagram of the proposed DTC system with duty-ratio control
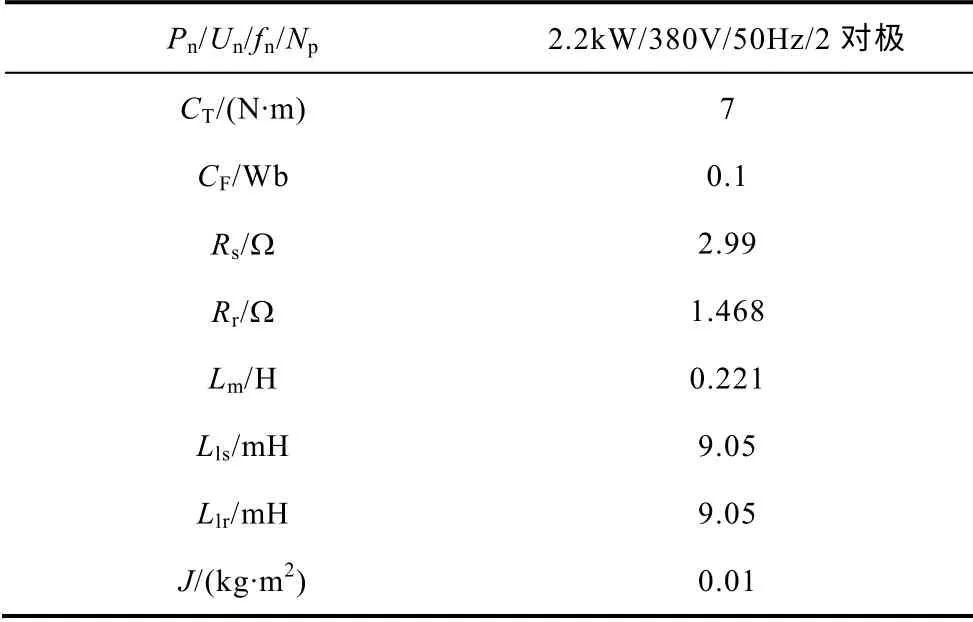
表 异步电机和控制系统参数 Tab. Induction motor and system parameters
在“占空比控制”模块中,所选有效电压矢量的占空比由式(14)~式(16)和式(18)计算出。一旦得到占空比d,在此采样周期的前d 部分时间应用所选有效电压矢量,剩余的时间则应用零电压矢量。为了减小开关损耗,当选出的有效电压矢量是V1(100)、V3(010)和V5(001)时,紧随其后的零电压矢量为V0(000),其他情况下为V7(111)。另外需要注意的是,当转矩不处于稳态时,由式(14)~式(16)计算出的d 值可能超出0~1 的范围。当d>1 时,令d=1;当d<0 时,令d=0。
图4 给出了异步电机从静止起动到1 050r/min和0.3s 时突加7N·m 负载时的仿真波形,包括传统DTC 和各种基于占空比控制的DTC。图中从上到下的曲线依次是有效电压矢量的占空比、定子磁链和电磁转矩。各种方法中转矩无论是在起动时刻还是在负载转矩突变时刻,都表现出相同迅速的转矩动态响应。其中,在稳态运行时传统DTC 方法的转矩脉动最大,几乎达到了6N·m,其次是直接平均转矩控制方法,大约为4N·m,最小转矩脉动DTC 方法比无差拍DTC 方法的转矩脉动要小,但效果不是很明显,转矩脉动都在近似3N·m 左右,而其占空比的计算式要比无差拍方法复杂得多,三种经典占空比确定DTC 方法的磁链脉动与传统DTC 方法没有明显的差别,因为它们在占空比的确定中都没有考虑对磁链的控制。本文所提的新方法同时减小了转矩和磁链脉动,转矩脉动大约为2N·m,并且通过对零电压矢量的合理选择减小了开关损耗。
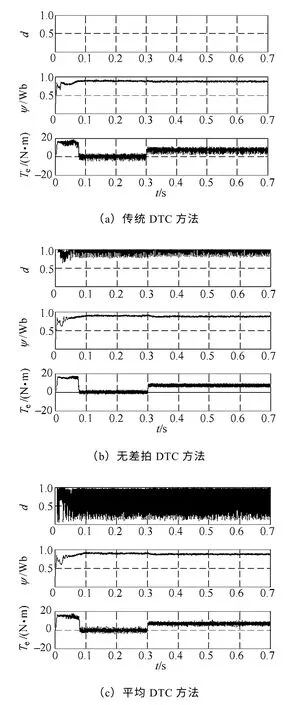

图4 各种占空比控制方法与传统DTC 方法的比较 Fig.4 Comparative study of various duty ratio control methods with conventional DTC
7 实验结果
为了进一步验证本文所提新占空比控制 DTC方法的可行性,在两电平逆变器馈电的异步电机驱动系统中进行了实验。为了获得较好的比较效果,实验中传统DTC 方法采样频率使用20kHz,而新方法使用的采样频率为10kHz。控制器采用32 位浮点DSP(TMS320F28335),可以方便地实现本文的控制算法。另外控制板上还扩展了4 通道的D-A,用于内部变量观测。实验中除电流采用电流探头直接测得外,其他变量都是通过12 位D-A 输出到泰克示波器上显示。异步电机和控制系统参数与表1 中所列相同。
首先研究系统在不同转速时的稳态性能。图5给出了传统DTC 和本文所提新方法在10%额定转速和100%额定转速满载时的稳态响应波形。图中曲线从上到下依次为电机转速、电磁转矩、定子磁链和定子电流。可以看出,不论是在高速还是在低速时,基于新型占空比控制的DTC 相比传统DTC的转矩脉动都有明显减小,而磁链脉动虽有减小,但效果不如仿真明显,基本证实了本文所提方法的有效性。

图5 新占空比控制方法与传统DTC 方法稳态波形 Fig.5 Steady-state waveforms of the new duty ratio control and conventional DTC method
图6 给出了传统DTC 和新方法在空载时从静止到1 500r/min 的起动波形,通过对PI 速度控制器进行限幅,电机很快达到额定转速。比较发现两者的动态响应过程没有明显差别,从而证明新方法保持了传统DTC 方法动态响应迅速的优点。
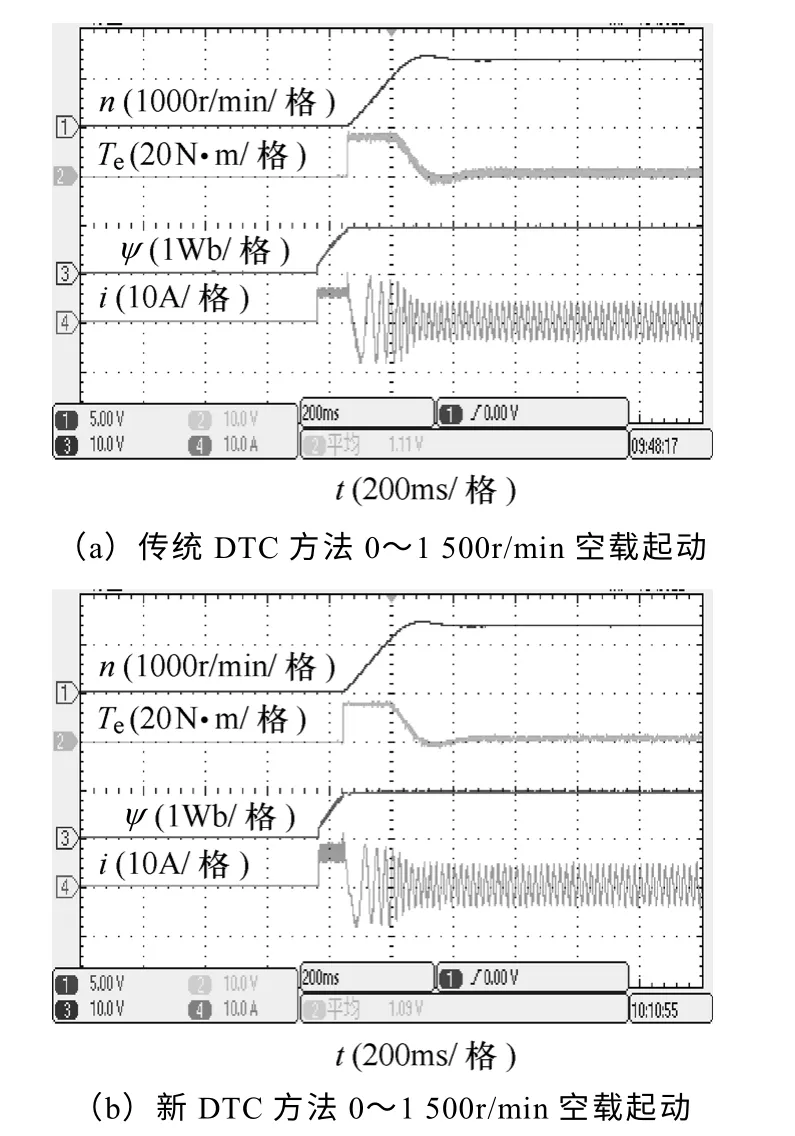
图6 新占空比控制方法与传统DTC 方法起动波形 Fig.6 Starting waveforms of the new duty ratio control and conventional DTC method
图7 给出了传统DTC 和所提新方法在额定转速运行时突加减负载的波形,对比发现,新方法同样表现出很强的抗干扰能力,动静态性能十分良好。

图7 新占空比方法与传统DTC 方法突加减负载波形 Fig.7 Step and subtract load waveforms of the new duty ratio control and conventional DTC method
8 结论
本文针对异步电机,在比较研究三种经典占空比控制方法性能的基础上,提出了一种对转矩和磁链误差进行同时优化的占空比控制方法。为了进一步改善系统性能,使用基于全阶观测器的方法估计定子磁链,可以在全速域范围内准确的观测磁链。仿真和实验结果表明,这种在占空比控制中对转矩和磁链误差同时进行优化的新型DTC 策略不但能够有效地减小传统DTC 的转矩和磁链脉动,而且保持了传统DTC 响应迅速、控制简单的优点,改善了传统DTC 的控制性能。
[1] Casadei D,Profumo F,Serra G,et al.FOC and DTC:two viable schemes for induction motors torque control[J].IEEE Transactions on Power Electronics,2002,17(5):779-787.
[2] Takahashi I,Noguchi T.A new quick-response and high-efficiency control strategy of an induction motor[J].IEEE Transactions on Industry Applications,1986,22(5):820-827.
[3] Depenbrock M.Direct self-control(DSC) of inverter- fed induction machine[J].IEEE Transactions on Power Electronics,1988,3(4):420-429.
[4] Buja G S,Kazmierkowski M P.Direct torque control of PWM inverter-fed AC motors—a survey[J].IEEE Transactions on Industrial Electronics,2004,51(4):744-757.
[5] Tiitinen P,Surandra M.The next generation motor control method,DTC direct torque control[C].Proc of Int Conf Power Electron,Drives and Energy Syst for Ind Growth,New Delhi,India,1996:37-43.
[6] Lai Yenshin,Chen Jianho.A new approach to direct torque control of induction motor drives for constant inverter switching frequency and torque ripple reduction [J].IEEE Transactions on Energy Convers,2001,16(3):220-227.
[7] Lascu C,Trzynadlowski A.Combining the principles of sliding mode,direct torque control,and space- vector modulation in a high performance sensorless ac drive[J].IEEE Transactions on Industry Applications,2004,40(1):170-177.
[8] Habetler T G,Profumo F,Pastorelli M et al.Direct torque control of induction machines using space vector modulation[J].IEEE Transactions on Industry Applications,1992,28(5):1045-1053.
[9] Kenny B,Lorenz R.Stator- and rotor-flux- based deadbeat direct torque control of induction machines [J].IEEE Transactions on Industry Applications,2003,39(4):1093-1101.
[10] Zhang Yongchang,Zhu Jianguo.Direct torque control of permanent magnet synchronous motor with reduced torque ripple and commutation frequency[J].IEEE Transactions on Power Electronics,2011,26(1):235-248.
[11] Flach E,Hoffmann R,Mutschler P.Direct mean torque control of an induction motor[C].Proc European Power Electronics and Applications(EPE),Trondheim,Norway,1997:672-677.
[12] Kang J K,Sul S K.New direct torque control of induction motor for minimum torque ripple and constant switching frequency[J].IEEE Transactions on Industry Applications,1999,35(5):1076-1082.
[13] 杨家强,黄进.异步电动机直接转矩控制转矩脉动最小化方法研究[J].电工技术学报,2004,19(9):23-29.
Yang Jiaqiang,Huang Jin.Research on torque ripple minimization strategy for direct torque control of induction motors[J].Transactions of China Electrotech- nical Society,2004,19(9):23-29.
[14] Romeral L,Arias A,Aldabas E,et al.Novel direct torque control(DTC) scheme with fuzzy adaptive torque- ripple reduction[J].IEEE Transactions on Industrial Electronics,2003,50(3):487-492.
[15] 刘军,刘丁,吴浦升,等.基于模糊控制调节电压矢量作用时间策略的永磁同步电机直接转矩控制仿真研究[J].中国电机工程学报,2004,24(10):148-152.
Liu Jun,Liu Ding,Wu Pusheng,et al.The simulation analysis of permanent magnet synchronous motor based on the strategy of modulating the time of voltage vector[J].Proceedings of the CSEE,2004,24(10):148-152.
[16] Kouro S,Cortes P,Vargas R,et al.Model predictive control—a simple and powerful method to control power converters[J].IEEE Transactions on Industrial Electronics,2009,56(6):1826-1838.
[17] Geyer T,Papafotiou G,Morari M.Model predictive direct torque control part I:concept,algorithm,and analysis[J].IEEE Transactions on Industrial Electronics,2009,56(6):1894-1905.
[18] Drobnic K,Nemec M,Nedeljkovic D,et al.Predictive direct control applied to AC drives and active power filter[J].IEEE Transactions on Industrial Electronics,2009,56(6):1884-1893.
[19] Miranda H,Cortes P,Yuz J,et al.Predictive torque control of induction machines based on state-space models[J].IEEE Transactions on Industrial Electronics,2009,56(6):1916-1924.
[20] Kubota H,Matsuse K,Nakmo T.DSP-based speed adaptive flux observer of induction motor[J].IEEE Transactions on Industry Applications,1993,29(2):344-348.
[21] Yang G,Chin T H.Adaptive-speed identification scheme for a vector-controlled speed sensorless inverter- induction motor drive[J].IEEE Transactions on Industry Applications,1993,29(4):820-825.
[22] Jehudi M,Jan A M.Speed-sensorless direct torque control of induction motors using an adaptive flux observer[J].IEEE Transactions on Industry Applica- tions,2000,36(3):778-785.
