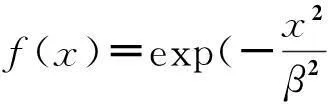基于低采样率浮动车数据的全局投票地图匹配算法

杨旭华，汪向飞

(浙江工业大学 计算机科学与技术学院，浙江 杭州 310023)

基于低采样率浮动车数据的全局投票地图匹配算法

杨旭华，汪向飞

(浙江工业大学 计算机科学与技术学院，浙江 杭州 310023)

摘要：针对现有地图匹配算法在低采样率时错误率较高的问题，提出一种全局投票地图匹配算法.算法在浮动车GPS轨迹数据的基础上，充分考虑道路网络的拓扑结构和不同距离的GPS轨迹点对匹配过程的影响.算法考虑道路网络的几何特性和拓扑结构，首先得出作为初始结果的静态匹配矩阵，定义距离加权函数对静态匹配矩阵进行修正，得到动态匹配矩阵，在此基础上进行全局投票，找出最优轨迹作为地图匹配的结果.最后采用杭州出租车数据对算法进行验证，结果显示：在采样率低情况下，算法能够充分利用已有信息，得到较好的地图匹配效果.

关键词：浮动车；低采样率；拓扑信息；距离加权；全局投票；地图匹配

A global-voting map matching algorithm for low-sampling-rate

floating car data

YANG Xuhua, WANG Xiangfei

(College of Computer Science and Technology, Zhejiang University of Technology, Hangzhou 310023, China)

Abstract:Since the existing floating car map-matching algorithms lead to high error rate when GPS data sampling rate is low, a global-voting map matching algorithm is proposed. Based on floating car GPS track data, the algorithm takes a full consideration on the impact of the topology of the road network and the GPS track points at different distances on the matching process Firstly, considering the influence of geometric and topological information of road network, a static matching matrix as initial results are gotten. Then, a distance weighting function is defined to revise the static matching matrix and built a dynamic matching matrix.Then an efficient global voting algorithm is used to identify the optimal trajectory as map matching result. Finally, the algorithm is verified on Hangzhou taxi data. Results show that this algorithm can make full use of existing information and has a good perform on map matching.

Keywords:floating car; low-sampling-rate; topological information; distance weighting; global-voting; map matching

浮动车一般是指安装了GPS轨迹定位装置并行驶在城市主干道上的公交汽车和出租车.浮动车技术是近年来兴起的一种动态交通信息检测的技术，是近年来智能交通系统中所采用的获取道路交通信息的先进技术手段之一[1].浮动车可以定期将车辆编号、时刻、方向、经纬度坐标等数据传送到调度中心,经过信息处理，可以方便地获得整个城市路网的实时交通信息.但是由于GPS轨迹设备自身会存在定位误差和采样误差，GPS轨迹点偏离道路的情况在所难免[2].地图匹配算法是浮动车数据处理的关键技术之一，它可以最大程度地校正GPS轨迹卫星定位所产生的误差，从而矫正车辆轨迹偏离道路的现象，将GPS轨迹数据转化为道路的交通信息.

传统地图匹配算法[3-5]采用很高的GPS轨迹采样间隔数据，匹配的正确率才得以保证.但在实际应用中,由于节约能源以及浮动车本身特性等原因，返回给调度中心的数据往往是低采样率的.在低采样率的情况下(2 min)，车辆的速度仅为30 km/h，两个GPS轨迹点之间的距离为1 000 m，尤其是在复杂的城市道路网络中，GPS轨迹点之间的关联信息会大部分丢失，给现有的地图匹配算法带来极大的挑战[6].另外一方面，考虑几何特性的地图匹配算法[7-9]，在匹配过程中，这些算法又可以分为点对点的匹配、点对曲线的匹配、曲线对曲线的匹配.在现代复杂的道路网络中，存在大量多车道，高架桥，分岔路情况，这些只考虑道路的几何特性的算法很容易出错.因此，传统的地图匹配算法不能很好解决低采样率的浮动车数据的匹配过程，针对上述问题，设计一种适应度更高、鲁棒性更强的全局投票地图匹配算法.

1全局投票地图匹配算法

近年来，低采样率浮动车数据地图匹配问题引起了很大关注.BRAKASTSOULS等提出一种针对相对低采样率(30 s)数据的地图匹配算法[10]，算法采用一种look-ahead技术来减少路段被遗漏的情况，从而提高准确率.CHEN Biyu等提出一种针对在线浮动车数据的多目标动态规划地图匹配算法[11],该算法考虑了GPS轨迹点之间的最短路径，减少待匹配轨迹点的候选路段来降低复杂度.WENK C等提出一种根据Frechet距离确定误差椭圆和匹配路径的匹配算法[12]，找出最有可能的轨迹点序列作为匹配结果，并运用在离线的地图匹配情况中.上述这些匹配算法不考虑全局GPS轨迹点之间的相互影响，在某个GPS轨迹点的匹配过程中，只利用该点本身的信息，或者仅仅考虑相邻GPS轨迹点对其匹配过程的影响[13].由于缺乏对整体道路网络拓扑结构的考虑，在复杂的道路环境和低采样率的浮动车数据情况下，GPS轨迹点之间的关联信息大量丢失，很难得到正确的匹配结果.尤其是当道路情况复杂时，例如多车道的情况下，很容易出现跨车道的情况.

实际上，浮动车数据不仅仅反映了车辆的位置信息，在某种程度上也反映了道路的拓扑结构信息以及GPS轨迹点之间的时间序列信息[14].因此这种针对低采样率GPS轨迹数据的全局投票地图匹配算法，在采样率低的情况下，充分考虑道路网络的拓扑结构，以及全局GPS轨迹点之间的关联信息，且根据GPS轨迹点之间的距离，对它们之间的影响程度进行加权处理，从而提高匹配的正确率.

1.1算法基本策略

这种全局投票地图匹配算法，有以下三个基本策略：

1) 考虑道路的拓扑结构

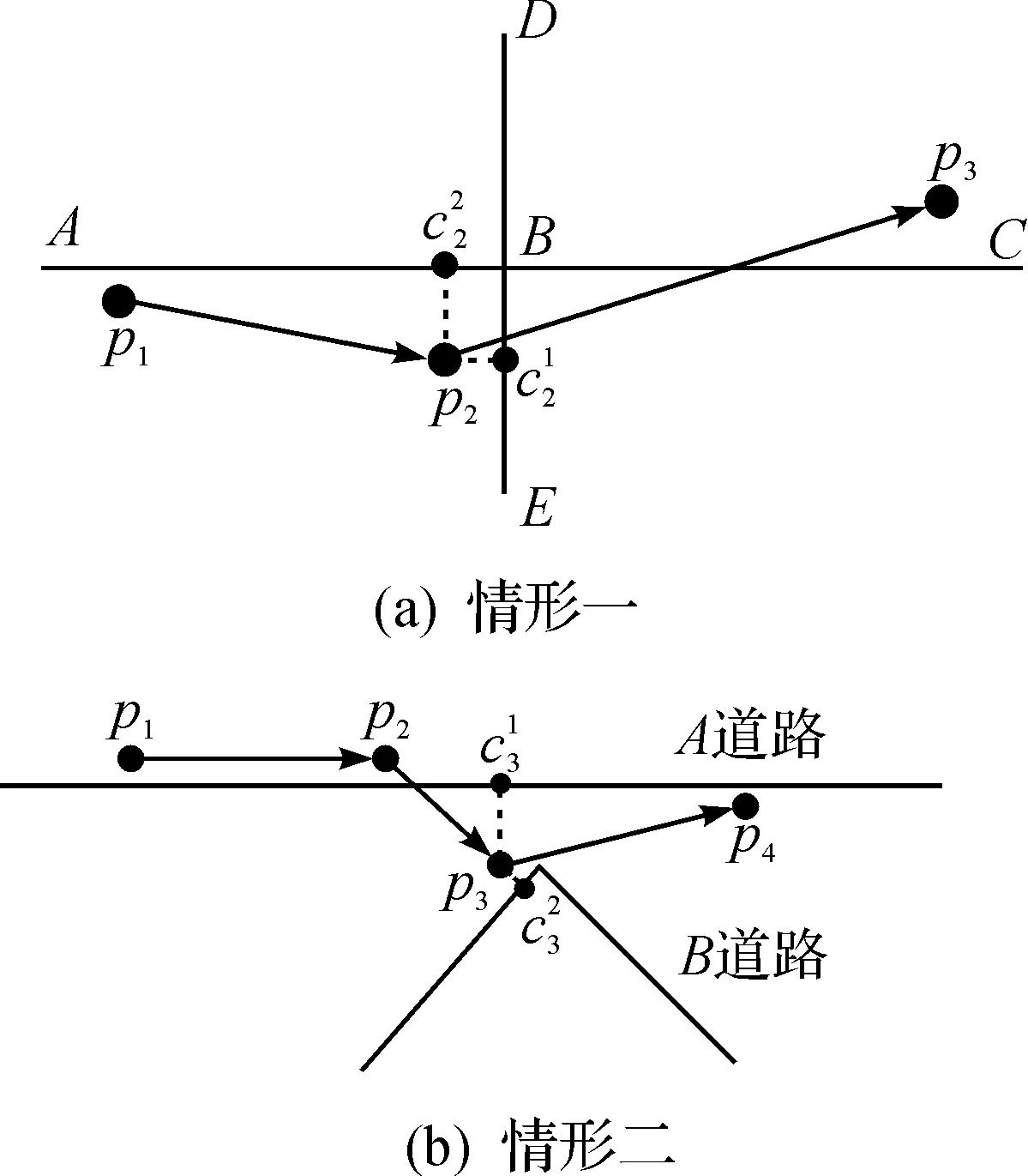
图1　考虑道路网络拓扑结构Fig.1　Consider the topological structure of road network

全局投票地图匹配算法从最短路径的角度考虑道路的拓扑结构.算法定义一个全新的匹配函数作为指标，不仅考虑GPS轨迹点之间的欧氏距离，还考虑候选点之间在道路网络中的最短路径，定义近距概率和连通概率计算得出静态匹配矩阵.在实际的城市交通网络中，考虑GPS轨迹点之间的最短路径，十分必要而且实用.

2) 考虑GPS轨迹点之间的相互影响

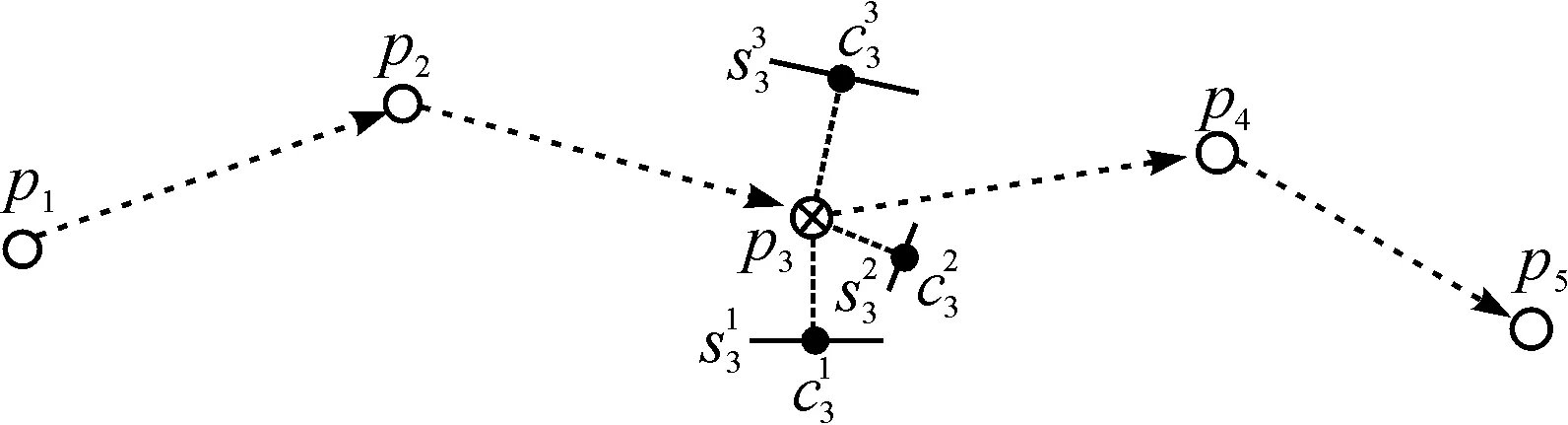
图2　不同距离空间位置相邻GPS轨迹点的相互影响Fig.2　Mutual influence of different distance adjacent GPS track point

全局投票地图匹配算法从全局投票的角度考虑GPS轨迹点之间的相关性.根据GPS轨迹点之间的欧氏距离和投影过程，产生每个GPS轨迹点的候选点集合，所有的GPS轨迹点相互之间进行投票过程，并且算法过程完全并行，只需要从候选点集合中投票产生正确匹配结果，而不需要计算大量的可能匹配结果，大大减小算法复杂度.

3) 考虑不同空间距离GPS轨迹点之间的加权影响

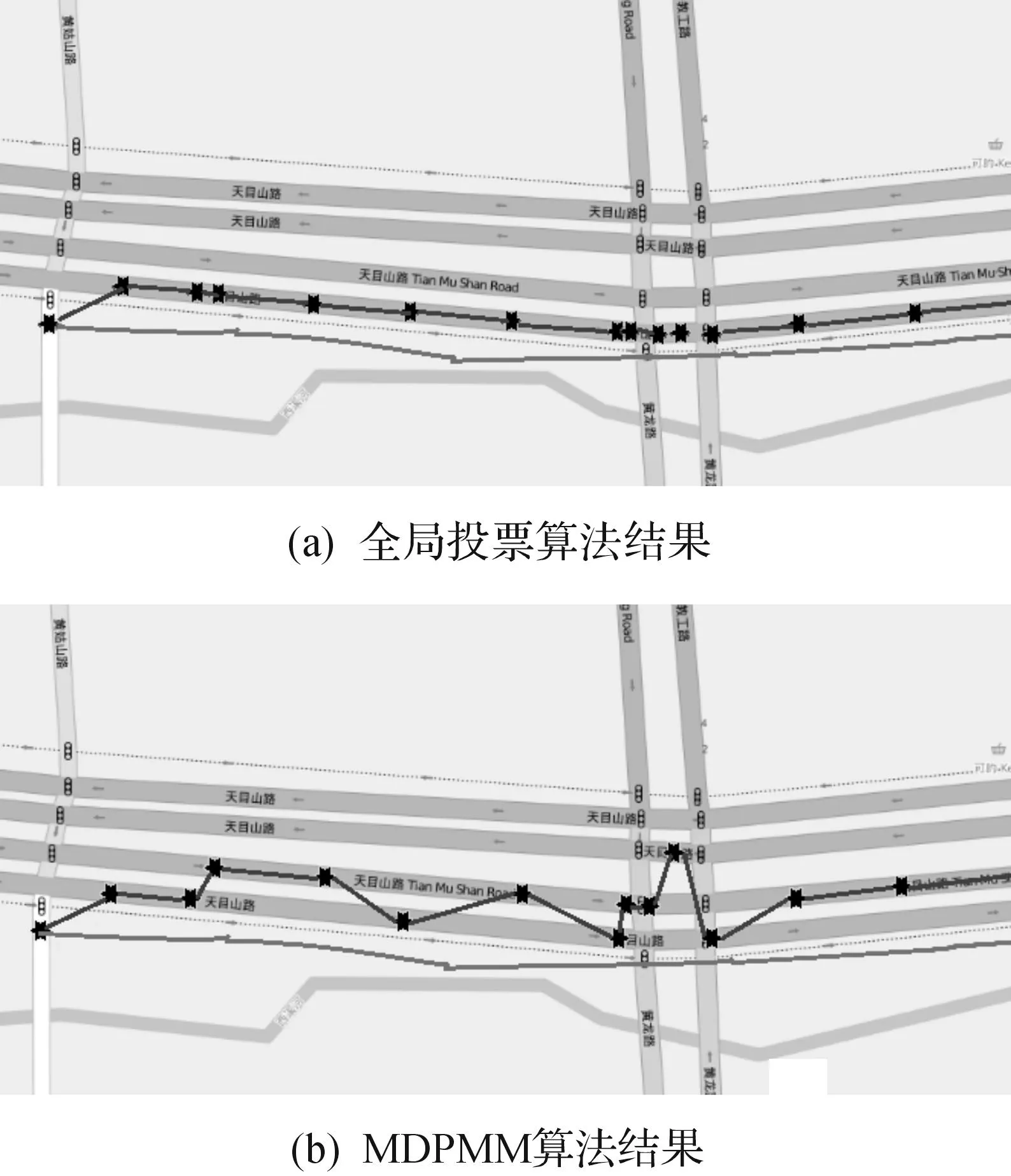
GPS轨迹点之间的相互影响的强弱程度是与它们之间的距离相关的.如图2所示，p1,p2,p4,p5在p3的地图匹配过程中，影响程度会因为它们距离p3的距离不同而不同.很明显，p2,p4对p3匹配过程的影响程度会大于p1,p5的影响程度.

全局投票地图匹配算法从加权的角度考虑GPS轨迹点之间的相关性.算法定义距离加权函数来代表GPS轨迹点之间距离越远，相互之间的影响程度越弱这一现象.并且在实验的基础上，得出加权函数不是简单的线性相关函数，而是更为有效的指数相关的距离加权函数.

1.2算法的具体步骤

这种全局投票算法在道路网络的模型下，首先计算当前GPS轨迹点可能匹配的候选集合.考虑集合中候选点的近距概率和连通概率，得出静态匹配矩阵.再考虑GPS轨迹点之间距离的不同导致影响程度的不同，定义距离加权函数，得出加权匹配矩阵，在此基础上，各个GPS轨迹点之间相互进行单点投票过程，完成匹配算法.具体可以分为5个步骤,如图3所示.

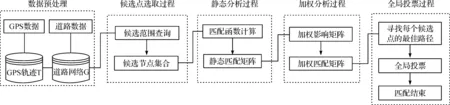
图3　算法流程图Fig.3　The algorithm flow chart

1) 数据预处理，完成道路网络G的构建以及GPS数据T整理.

2) 选取候选节点，根据路段投影过程，得出每个GPS轨迹点的候选集合.

3) 静态分析过程，定义匹配函数F，对每个GPS轨迹点的候选集合进行计算，得出静态匹配矩阵.

4) 加权分析过程，对每一个GPS轨迹点，定义距离加权函数，以此来反映GPS轨迹之间距离和影响程度之间的关系.经过全局计算，得出动态匹配矩阵.

5) 全局投票，在每个GPS轨迹点对应的动态匹配矩阵中，进行单点投票过程.同时，所有单点投票过程并行运算，最后进行汇总，得出全局投票结果.

1.2.1数据预处理

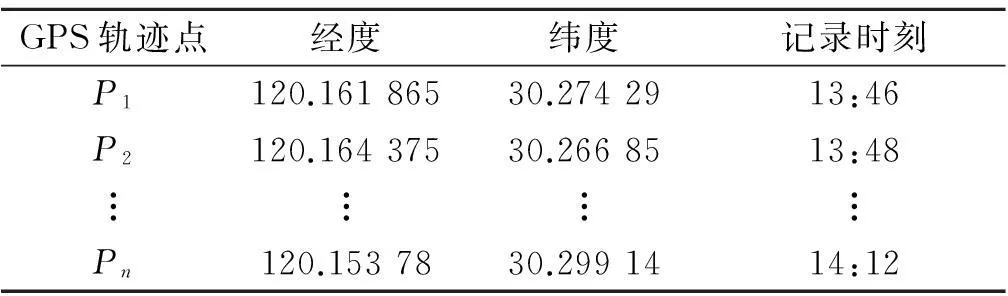
表1　GPS轨迹点数据

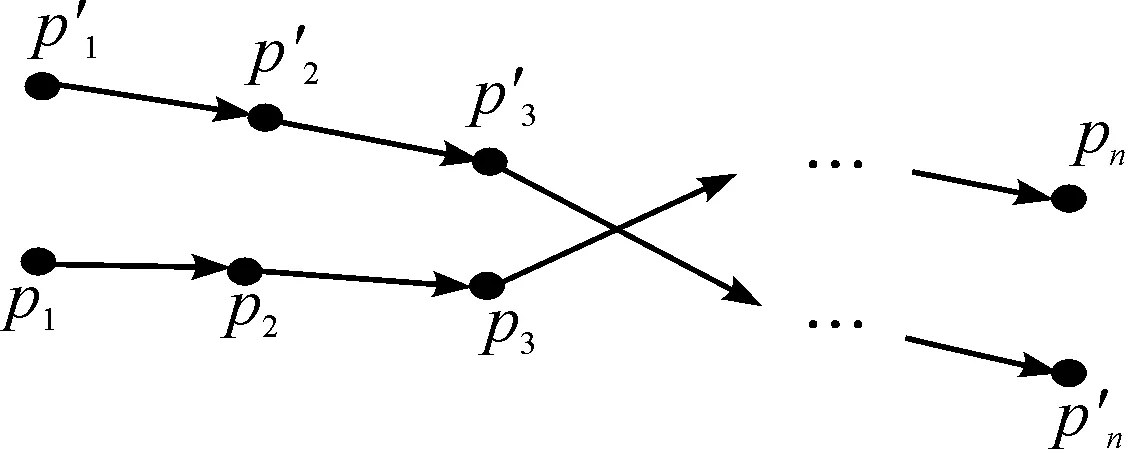
图4　GPS轨迹数据Fig.4　GPS track data

道路网络定义为一个有向图G(V,E)，其中V为道路的交叉点、起点或终点，E为被两个相邻交叉口分隔出的路段，每个路段包含起始点、结束点、路段长度.根据道路网络，从而定义一条路径P为：在道路网络中，选取两个节点Vi,Vj，找到一条互相连接的路段集合E1→E2→E3→…→En，并且路段E1的起点为Vi，路段En的终点为Vj.

根据上述定义，将已有的GPS轨迹数据和道路数据进行预处理，分别得到GPS轨迹T和道路网络G.同时可以得出：地图匹配算法的目的在于，输入一个GPS轨迹T和道路网络G(V,E)，找出一条路径P去匹配轨迹T.

1.2.2选取候选节点

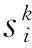
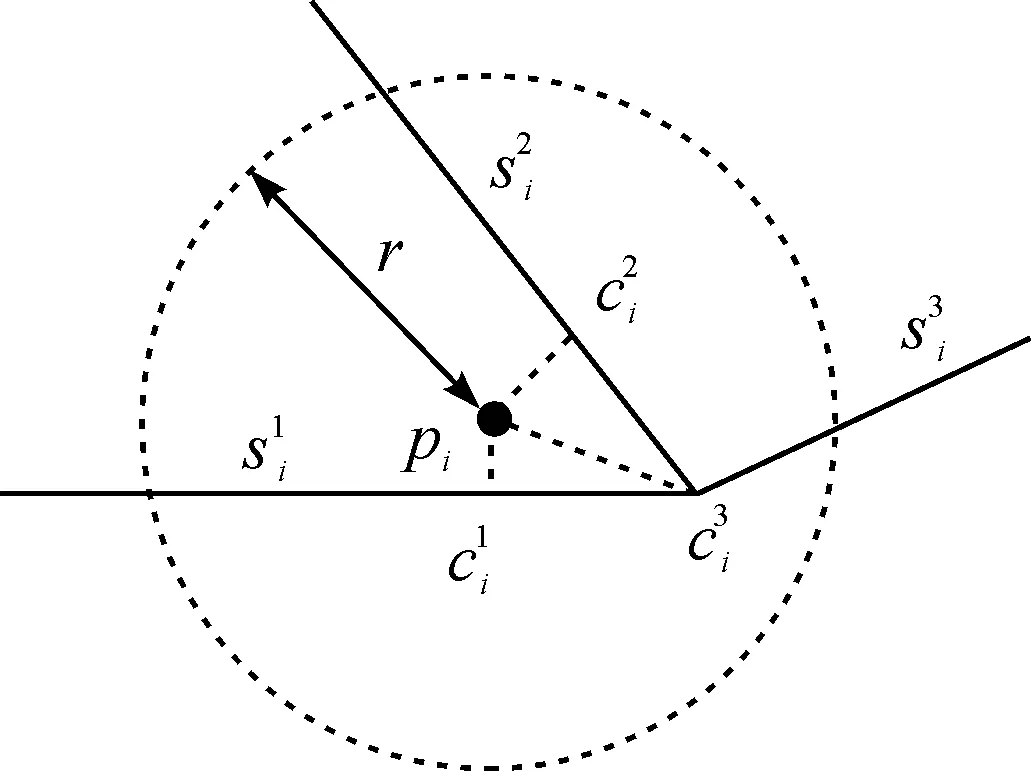
图5　候选节点选取Fig.5　Candidate points selection

1.2.3静态分析过程

(1)

得到每个候选节点的近距概率后，为了避免错误，考虑道路网络的拓扑结构，根据GPS轨迹点之间的最短路径长度，定义两个候选节点之间的连通概率CP为

(2)

综上所述，近距概率考虑了道路网络的几何性质，连通概率考虑了道路网络的拓扑结构.在这两者的基础上，定义一个匹配函数F，其表达式为

(3)

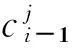
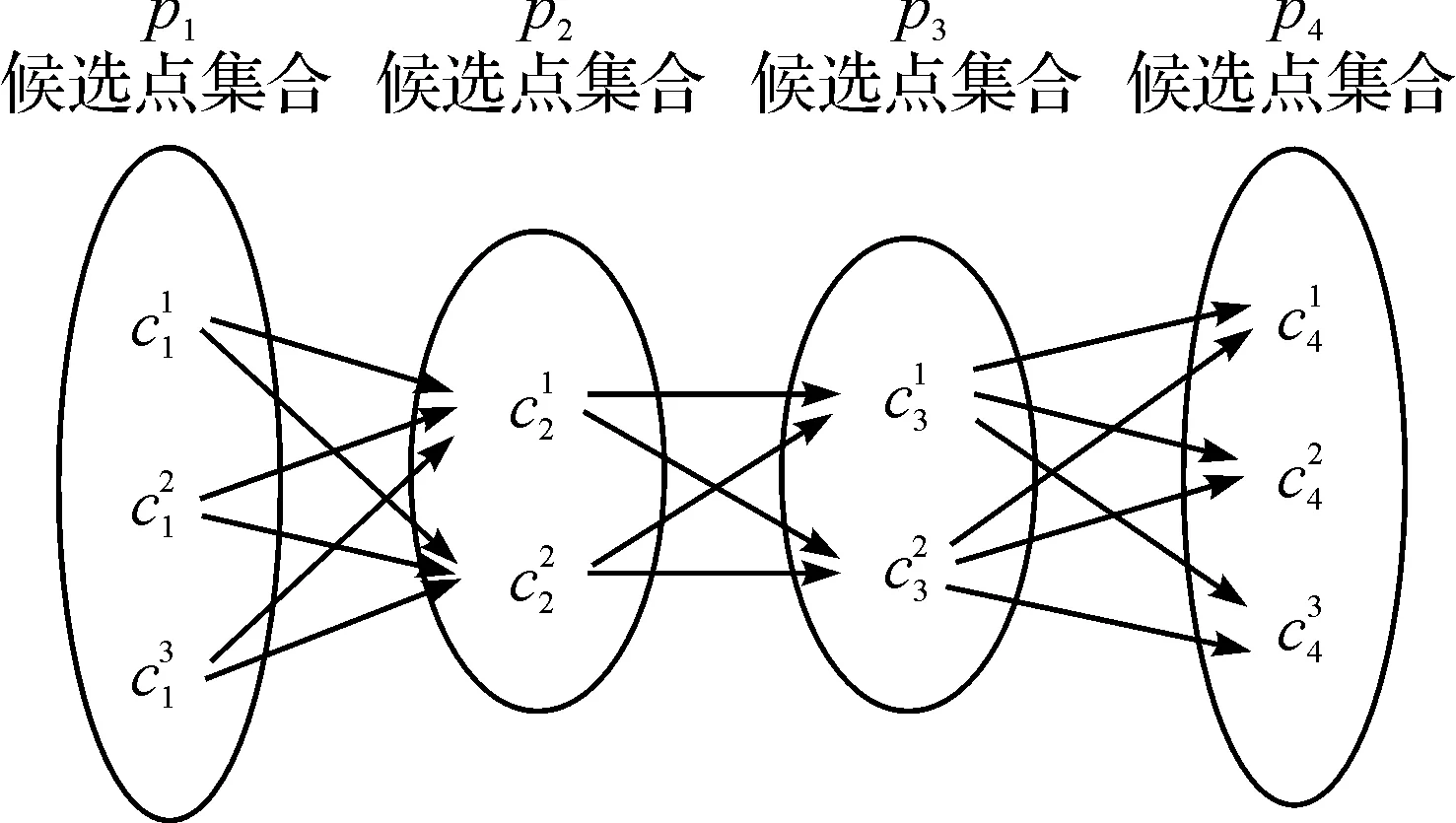
图6　候选节集合Fig.6　Candidate points sets

(4)

(5)

其中：1≤j≤m,1≤k≤n,m,n分别为ci-1,ci的候选节点总个数.比如针对p1→p2→p3→p4，为了方便说明，假设有

依次得出M3,M4，最终的静态匹配矩阵为

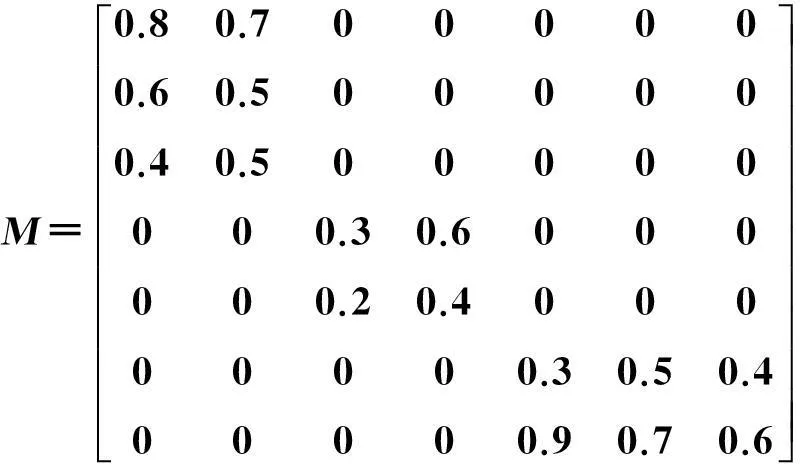
1.2.4加权分析过程

在步骤3得到的静态匹配矩阵的基础上，考虑GPS轨迹之间的距离越远，它们之间互相的影响越弱.因此，针对每个轨迹点pi，定义一个n-1维距离影响矩阵Wi为

(6)

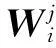
1)f(0)=1.

2)f(∞)=0.

3) 0

为了方便说明，选取f=2-|i-j|说明算法过程，i,j为轨迹点pi,pj的下标.定义动态匹配矩阵Gi(1≤i≤n)为

(7)

1.2.5全局投票过程

表2　投票结果

2实验结果与分析

2.1实验数据来源

实验中，如图7(a)所示，在杭州道路网络上进行实验，道路网络数据通过开源网站OpenStreetMap以及高德地图API获取.另外，如图7(b)所示，待匹配轨迹数据选用杭州真实的出租车GPS轨迹数据，数据格式如表3所示.

图7　实验数据Fig.7　Experimentation data

ID车牌号经度纬度速度/(km·h-1)方向记录时刻3879981103浙AT1239120.11283330.31798330.24180.0007:34:523879981104浙AT6105114.49003633.8530730.37350.0007:34:53

2.2对比过程

为了评价算法的匹配效率，选取一种点对点地图匹配算法[8]和一种多目标动态规划地图匹配算法[12]作为比较对象.这种基于点对点距离的地图匹配算法(P2PMM)，先找到候选点和候选路段，计算轨迹点和候选点之间的距离，选取距离最短的候选点作为匹配结果.另外，这种多目标动态规划地图匹配算法(MDPMM)会考虑节点之间的最短路径，但是只考虑相邻邻居节点对匹配过程的影响.定义正确匹配率，即正确匹配GPS轨迹点数量与待匹配GPS轨迹点总数的比例，以此来对比不同算法的匹配准确率.

实验过程中，每次选取一辆出租车时间间隔为2 min的20个点作为待匹配GPS轨迹点，每次实验在GPS轨迹点经纬度坐标加上一个与时间戳有关的随机数，进行2 000次实验.将每次匹配结果与刚开始设定的正确匹配结果(人为标识)进行对比，误差不超过1M认定问匹配正确.

2.3结果

首先给出在道路网络中，杭州出租车数据经过全局地图匹配算法计算以后的可视化结果(共匹配3 000辆出租车数据，每辆出租车选取20个GPS轨迹点).实验结果表明：杭州出租车数据很好的匹配到道路上，正确率达到90%左右.如图8(b)所示，在道路情况相对复杂的情况下，比如多车道，MDPMM很难得到正确的匹配结果，会出现复杂的跨车道情况，然而全局投票匹配后的结果如图8(a)所示，很好的避免了跨车道情况.其中不带标记的线为GPS轨迹数据，带星形标记的线为地图匹配结果.

图8　多车道情况下匹配结果Fig.8　Multi-Lane matching result

图9　不同地图匹配算法Fig.9　Different map matching algorithm

图10　不同距离加权函数Fig.10　Different distance weighted function

3结论

这种全局投票地图匹配算法针对低采样率的浮动车数据，在分析已有地图匹配算法的基础上，结合道路的拓扑结构，综合考虑了GPS轨迹点之间的相互作用，并且定义了距离加权函数来体现节点之间距离和相互影响权重之间的关系，提出一种全局投票地图匹配算法.该算法运用于杭州真实的出租车GPS轨迹数据，获得了良好的地图匹配效果.

参考文献：

[1]赵敬洋，郭明飞，郭海峰，等.基于典型行车路线理论的城市交通中诱导屏选址优化方法研究[J].浙江工业大学学报，2010，38(5):586-590.

[2]陈晓眯，孟志青，徐杰．基于混合禁忌搜索算法的动态车辆路径研究[J].浙江工业大学学报,2009,37(5):580-581.

[3]SU Jie, ZHOU Dongfang, YUE Chunsheng. Real-time map-matching algorithm in GPS navigation system for vehicle[J].Acta Geodaetica et Cartographica Sinca,2001,30(3):252-256.

[4]TANG Jinjun, CAO Kai. An adaptive trajectory curves map-matching algorithm[J]. Acta Geodaetica et Cartographica Sinca,2008,37(3):308-315

[5]XU H, LIU H C, TAN C W,BAO Y L. Development and application of an enhanced kalman filter and global positioning system error-correction approach for improved map-matching[J]. Journal of Intelligent Transportation Systems,2010,14(1):27-36.

[6]TOMIO M, DAISUKE K, TOSHIYUKI Y. Development of map matching algorithm for low frequency probe data[J]. Transportation Research,2012,22:132-145.

[7]WHITE C, BERNSTEIN D, KORNHAUSER A L. Some map matching algorithms for personal navigation assistants[J]. Transportation Research Part C,2000,8:91-108.

[8]YIN H B, WOLFSON O A weight-based map matching method in moving objects databases[C]//In Proceedings of the International Conference on Scientific and Statistical Database Management. Chicago: Scientific and Statistical Database Management Press,2004:437-410.

[9]HONG W B, CHEN C Y, PENG J W. Improvements of driver fatigue detection system based on eye tracking and dynamic template matching[J]. WSEAS Transactions on Information Science and Application,2012,9(1):14-23.

[10]BRAKATSOULS D P, SALAS R, WENK C. On map-matching vehicle tracking data[C]//In 31st International Conference on Very Large Databases. San Antonio：University of Texas Press，2005:853-864.

[11]CHEN Biyu , YUAN Hui, LI Qingquan, et al. Map-matching algorithm for large-scale low-frequency floating car data[J]. International Journal of Geographical Information Science,2014,28(1):22-38.

[12]WENK C, SALAS R, PFOSER D. Addressing the need for map-matching speed: localizing global curve-matching algorithm[C]//In 18th International Conference on Scientific and Statistical Database Management. San Antonio：University of Texas Press，2006:379-388.

[13]GREENFELD J S. Matching GPS observations to locations on a digital map[J]. Transportation Research Board,2002,27(1):13-16.

[14]GUO L M, LUO D Y. Study on map matching technology in wireless position[J]. Computer Engineering and Applications,2009,45(18):25-27.

[15]QUDDUS M A, WASH INGTON Y O, ROBERT B N. Current map-matching algorithms for transport applications: state-of-the art and future research directions [J].Transportation Research Part C,2007(15):312-328.

[16]杨旭华,李传告,陈光.基于K-最短路径的交通网络传输性能分析[J].浙江工业大学学报，2014,42(3):249-256.

(责任编辑：刘岩)

中图分类号：TP13

文献标志码：A

文章编号：1006-4303(2015)03-0318-08

作者简介：杨旭华(1971—),男，浙江余姚人，教授，研究方向为复杂网络和智能效能，E-mail:xhyang@zjut.edu.cn.

基金项目：国家自然科学基金资助项目(61374152)；浙江省公益性技术应用研究计划项目(2012C23126)

收稿日期：2015-01-22