一阶多次波聚焦变换成像
2015-02-18刘学建刘伊克胡昊谢宋雷
刘学建, 刘伊克, 胡昊, 谢宋雷
1 中国科学院地质与地球物理研究所 中国科学院工程地质力学重点实验室, 北京 10002 2 中国科学院大学, 北京 100049 3 中国科学院南海海洋研究所, 广州 510301
一阶多次波聚焦变换成像
刘学建1,2, 刘伊克1, 胡昊1,2, 谢宋雷3
1 中国科学院地质与地球物理研究所 中国科学院工程地质力学重点实验室, 北京 10002 2 中国科学院大学, 北京 100049 3 中国科学院南海海洋研究所, 广州 510301
将多次波转换成反射波并按传统反射波偏移算法成像,是多次波成像的一种方法.聚焦变换能准确的将多次波转换为纵向分辨率更高的新波场记录,其中一阶多次波转换为反射波.本文对聚焦变换提出了两点改进: 1)提出局部聚焦变换,以减小存储量和计算量,增强该方法对检波点随炮点移动的采集数据的适应性; 2)引入加权矩阵,理论上证明原始记录的炮点比检波点稀疏时,共检波点道集域的局部聚焦变换可以将多次波准确转换成炮点与检波点有相同采样频率的新波场记录.本文在第一个数值实验中对比了对包含反射波与多次波的原始记录做局部聚焦变换和直接对预测的多次波做局部聚焦变换两种方案,验证了第二种方案转换得到的波场记录信噪比更高且避免了第一个方案中切聚焦点这项比较繁杂的工作.第二个数值实验表明:在炮点采样较为稀疏时,该方法能有效的将一阶多次波转换成反射波;转换的反射波能提供更丰富的波场信息,成像结果更均衡、在局部有更高的信噪比,以及较高的纵向分辨率.
聚焦变换; 多次波成像; 多次波消除
1 引言
传统的偏移算法往往只利用反射波对地下结构成像,多次波要在偏移之前的预处理中尽可能的减掉.实际上多次波在地下比反射波传播路径更长、覆盖范围更广(如图1).近年来,很多的学者致力于多次波成像的研究,发展出多次波地震干涉成像、多次波直接偏移成像、多次波聚焦变换成像等方法(Berkhout, 1993; Berkhout and Verschuur, 1994; Schuster et al., 2004; Guitton, 2002; Berkhout and Verschuur, 2006; Vasconcelos et al.,2008).甚至有的学者尝试利用多次波进行偏移速度分析(Manuel and Uren, 2001).多次波地震干涉成像、多次波聚焦变换成像都是先将多次波转换成反射波,然后按传统反射波偏移算法成像.

图1 反射波与多次波的传播路径Fig.1 Propagating paths of the primary and the multiple
地震干涉法最早可以追溯到1968年,Claerbout(1968)在二维模型上进行了被动震源地震记录的自相关实验,现已经取得了广泛的研究成果(Schuster, 2009).多次波地震干涉成像的简单流程为:首先将共炮点道集内(或共检波点道集内)的道记录两两之间做互相关生成虚拟炮记录,叠加相同位置处的虚拟炮记录,多次波转换成反射波和噪声(Wapenaar and Fokkema, 2006; Schuster, 2009),然后再按传统反射波偏移算法成像(Sheng, 2001; He et al., 2007; Jiang et al., 2007).地震干涉法的算法简单、计算效率高.然而,地震干涉法不够精确,生成的虚拟炮记录有大量的串声噪声.另一方面,虚拟炮记录同相轴的子波是原始地震记录同相轴子波的互相关.
Berkout等(1994)提出多次波直接偏移成像的思想.修改传统的单程波偏移或逆时偏移方法,可以很容易的实现多次波的直接偏移成像,其原理为:将包含反射波与多次波的原始道记录代替传统偏移算法中的点震源向地下正传,将多次波(或原始道记录)代替传统偏移算法中的反射波向地下反传,同一位置处的正传波场与反传波场互相关成像(Guitton, 2002; Muijs, 2007; Liu et al., 2011a, 2011b; Lu et al., 2011; Wang et al., 2014).该方法不需要提前将多次波转换为反射波,且有与传统反射波偏移方法相同的偏移计算效率.然而其在成像域产生的串声噪声和结构性假象较难消除.
聚焦变换从基于波动方程的表面多次波消减方法SRME(surface-related multiples elimination) (Verschuur et al., 1992; Berkhout et al., 1997; Verschuur and Berkhout,1997; 李鹏等, 2007)发展而来,由Berkhout和Verschuur(2003)首次提出,已应用到多次波聚焦变换消除、多次波成像和地震道插值等方面(Berkhout et al., 2004, 2006; Verschuur and Berkhout, 2005; Groenestijn and Verschuur, 2006).该方法将原始波场记录中的反射波能量聚焦到时间为零的点周围,准确的将一阶多次波转换为反射波,二阶多次波转换为一阶多次波,依次类推.在共炮点道集,反射波能量的聚焦点为炮点;在共检波点道集,反射波能量的聚焦点为检波点.聚焦变换是最小二乘意义上的变换,多次波转换的新波场记录具有很高的信噪比.切去聚焦点周围的能量,然后将新波场记录中的多次波(由二阶及更高阶的多次波转换而来)减去,得到的一阶多次波转换的反射波.将转换的反射波成像,实质上是对一阶多次波的反射位置成像.
本文提出了局部聚焦变换,增强了该方法对检波点随炮点移动的采集数据的适应性.引入加权矩阵后,本文验证了:当原始波场记录的炮点采样相对稀疏时,共检波点道集域的局部聚焦变换能将多次波准确转换成炮点与检波点有相同采样频率的新波场记录.传统反射波成像算法,我们采用的是对速度模型的横向变化及陡倾角适应性强的逆时偏移(Baysal et al., 1983; 胡昊等, 2013).
2 一阶多次波聚焦变换成像原理
2.1 聚焦变换基本原理
在炮点与检波点重合的观测系统上,用单频矩阵表示全波场的波场记录,波场矩阵的列存储共炮点或共检波点道集记录(如图2).忽略算符细节,用ΔP表示反射波波场记录,M表示多次波波场记录,P= ΔP+M=ΔXS+ΔXR∩ΔXS
+(ΔXR∩)2ΔXS+…
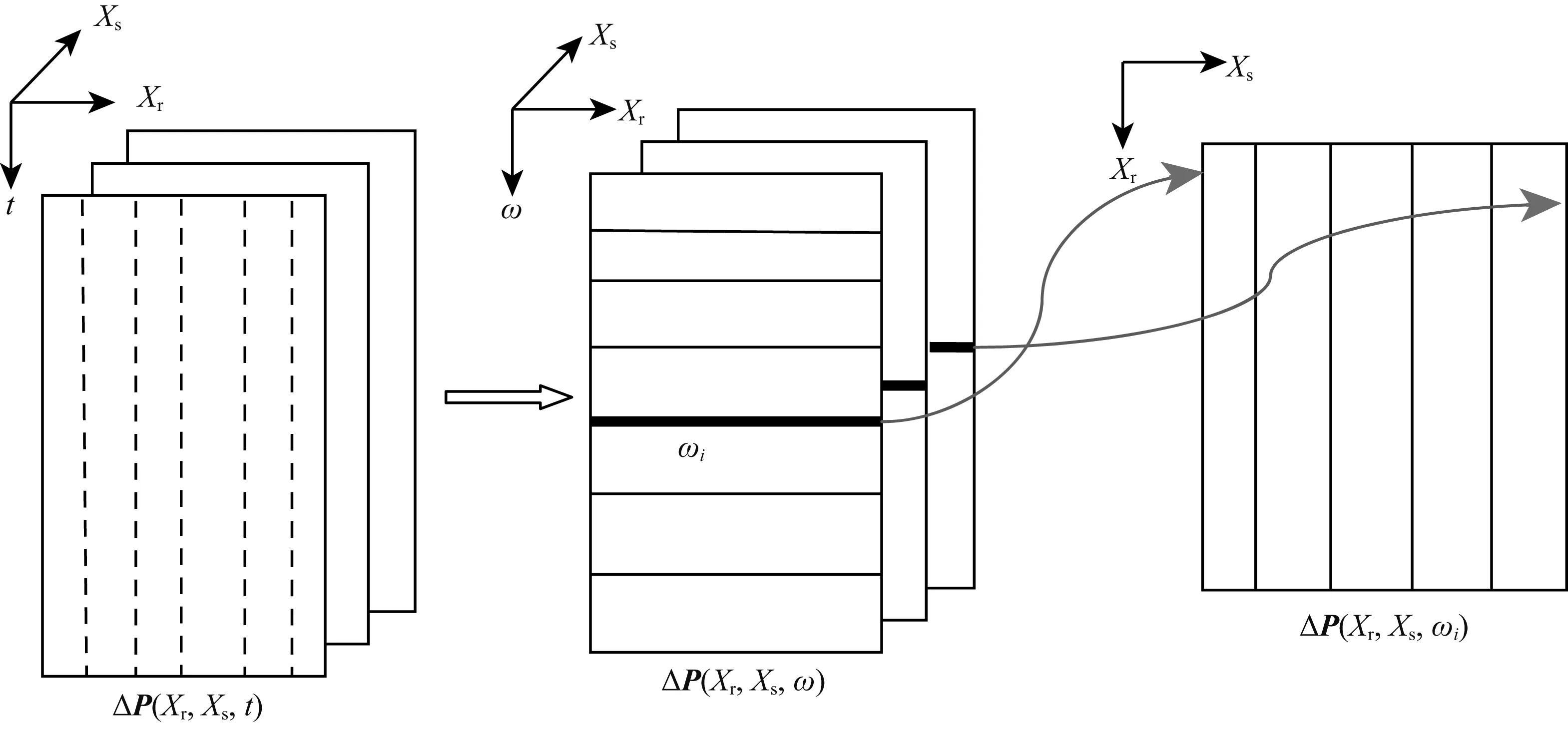
图2 频率域数据矩阵的结构(数据矩阵ΔP(xr, xs , ωi)的行列可以互换)Fig.2 Structure of data matrix in frequency domain, row and column of data matrix ΔP(xr, xs , ωi) are interchangeable
P表示包含反射波和多次波的原始波场记录,根据反馈迭代模型(Verschuur et al., 1992; Berkhout and Verschuur, 2003, 2006) (图3):
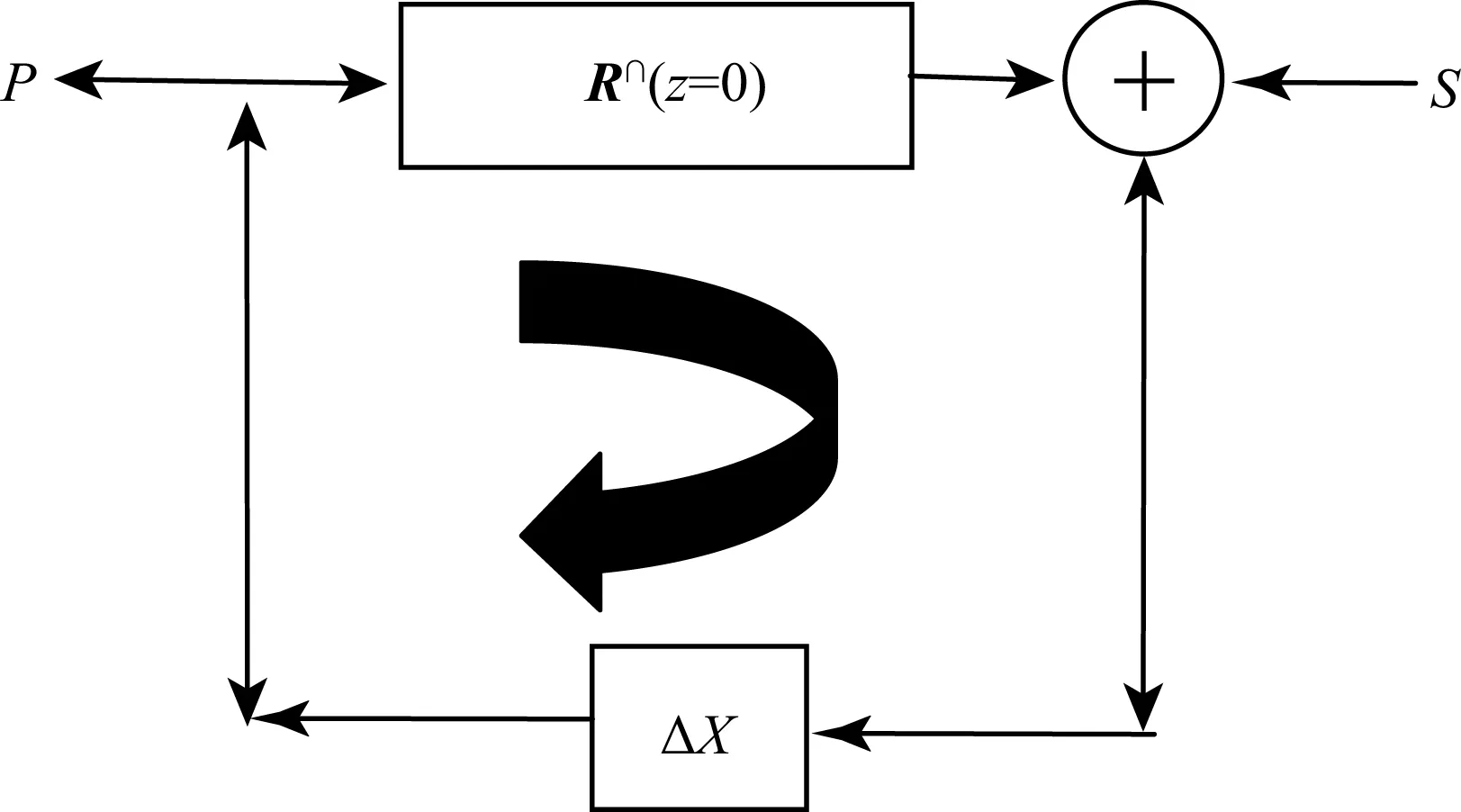
图3 反馈迭代模型Fig.3 The feedback model
ΔP=ΔXS,
(1)
(2)
(3)
其中:对角矩阵S为震源特性矩阵,对角元素为频率域的震源子波;ΔX表示脉冲震源在地下的一次响应;R∩为自由表面反射系数特性矩阵.
表面算符A记为:
(4)
引入表面算符,公式(2)、(3)改写为:
M=ΔPAΔP+(ΔPA)2ΔP+…
=ΔPA(ΔP+ΔPAΔP+…)
=ΔPAP′,
(5)
P=ΔP+ΔPAΔP+(ΔPA)2ΔP+…
=ΔP+ΔPA(ΔP+ΔPAΔP+…)
=ΔP+ΔPAP′.
(6)
显而易见,P′为缺少原始波场记录P中最高阶多次波的波场记录.当测线在自由表面之下时,自由表面的反射系数特性(R∩)包含在波场记录中,此时表面算符A记为:
(7)
聚焦变换定义为:
(8)

聚焦变换最小二乘意义上的稳定表达式为:
(9)
上标H表示复数矩阵的共轭转置,ε较为保证矩阵求逆计算稳定的较小正常数.
联立公式(5)、(6)、(8)、(9)可以推出:
(10)
(11)
(12)
单频矩阵I对应波场记录中聚焦点,反射波能量聚焦到该点周围.在共炮点道集域,聚焦点对应各炮的炮点;在共检波点道集域,聚焦点为相应的检波点.AP′为我们从多次波中还原得到的所有波场记录;其中一阶多次波转换为反射波,二阶多次波转换为一阶多次波,依次类推.A近似为震源特性矩阵的逆,因此聚焦变换具有去子波效应,多次波转换的新波场记录比原波场记录有更高的纵向分辨率.
2.2 聚焦变换的改进
2.2.1 局部聚焦变换
在检波点随炮点移动的观测系统中,若用一个矩阵存储全波场记录,存储量、计算量会相常的大.为了增强聚焦变换的适用性,我们提出局部聚焦变换:在逐个共炮点或共检波点道集记录上做聚焦变换.在炮点与检波点重合的情况下,局部聚焦变换表示为:
(13)
相应的:
(14)
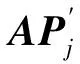
2.2.2 引入加权矩阵
用全波场记录矩阵的列存储共检波点道集记录,行存储共炮点道集记录.引入对角矩阵Λ做加权矩阵,表示炮记录的缺失:
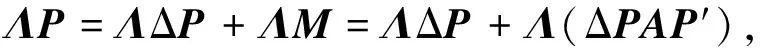
(15)
Λk,l=1,k=l,炮存在;
Λk,l=0,k=l,炮缺失;
Λk,l=0,k≠l.
(16)
当加权矩阵Λ的对角元素周期性的为1其余为0时,表示炮点比检波点稀疏的观测系统.联立公式(8)、(10)、(15)容易推导出:
Q=(ΛΔP)H[(ΛΔP)(ΛΔP)H+εI]-1(ΛP)
≈I+AP′
(17)
相应的:
AP′≈(ΛΔP)H[(ΛΔP)(ΛΔP)H+εI]-1(ΛM),
(18)
在检波点随炮点移动的观测系统上:
Qj=(ΛΔPj)H[(ΛΔPj)(ΛΔPj)H+εI]-1(ΛPj),
(19)

(20)
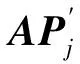
2.3 一阶多次波成像
(21)
在时间域将转换的反射波成像.将转换的反射波成像,实质上是对一阶多次波的反射位置成像.本文采用对速度模型的横向变化及陡倾角适应性强的逆时偏移成像(互相关成像条件),其基本原理为:
(22)
Ws(x,t)为时间正向延拓到地下的震源波场,Wg(x,t)为时间逆向延拓到地下的检波点波场.
3 模型算例
3.1 Pluto1.5模型的完整数据
Pluto1.5声波速度模型如图4,共1387炮,炮间距和道间距为22.86 m,检波点随炮点移动.以炮点位于7985 m的第350炮为例,在共炮点道集域对比如图5a、图5b所示的两种方案.如图6a为包含反射波与多次波的原始炮记录,图6b、图6c分别为通过SRME方法得到的炮记录的反射波和多次波.
按照图5a中的方案一,对如图6a中包含反射波与多次波的原始炮记录做局部聚焦变换(公式(13))得到新的波场记录(图7a).反射波聚焦到炮点周围,如图7a中水平箭头所指位置;一阶多次波转换为反射波,二阶多次波转换为一阶多次波,依次类推.减去炮点周围的能量即可得到多次波转换的新波场记录(图7b).按照图5b中的方案二,直接对如图6c中的多次波做局部聚焦变换(公式(14))得到多次波转换的新波场记录(图8a).相比原始波场记录,多次波转换的新波场记录(图7b、图8a)有更好的纵向分辨率,体现了聚焦变换的去子波效应.
由于SRME方法分离反射波与多次波过程中多次波能量的泄露(Berkhout and Verschuur, 2006),方案一的优势在于能利用完全无损失的多次波信息.然而,当采用方案一时,原始记录的反射波能量并非最佳聚焦,部分能量泄露到多次波转换的剖面中(如图7b中倾斜箭头所指位置).显然,图8a中的波场记录比图7b中波场记录有更高的信噪比.这一现象或许与采样数据的空间间隔不够小以及引入的稳定因子ε都使得聚焦变换不再完全准确有关.在方案一中经常需要人工切除聚焦点及其周围的能量,而这项工作非常繁杂.
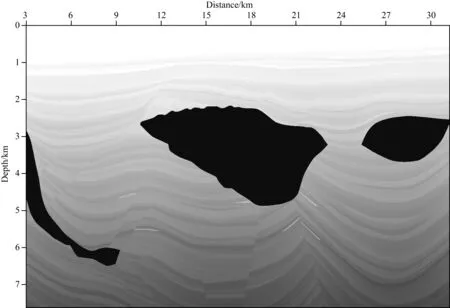
图4 Pluto1.5声波速度模型Fig.4 Acoustic wave velocity of pluto1.5 model

图5 局部聚焦变换(a)方案一和(b)方案二,(c)减去高阶多次波转换的多次波Fig.5 (a) First scheme and (b) second scheme for local focal transformation; (c) eliminate multiples transformed from high-order multiples
将多次波转换的波场记录(图8a)中的高阶多次波转换的多次波减去(如图5c)得到一阶多次波转换的反射波;对比图8a与图8b,图8a中箭头所指位置处的多次波较好的被消除.
3.2 Pluto1.5模型的抽稀数据
将原始炮集抽稀:保留炮号为奇数的原始记录,炮号为偶数的原始记录充零,此时炮间距是道间距的2倍.本例局部聚焦变换的工作流程采用如图5b所示的方案二,直接对多次波做局部聚焦变换.与算例1不同之处在于:算例2首先在共炮点道集域分离反射波与多次波记录;然后将反射波及多次波记录分别抽到共检波点道集域,炮记录的缺失在共检波点道集表现为数值为0的一个空道;多次波的局部聚焦变换在共检波点道集域内进行;图5c所示的消减高阶多次波转换的多次波在共检波点道集内进行;最后将一阶多次波转换的反射波抽回到共炮域.共检波点道集域的局部聚焦变换能够从多次波中提取原始波场记录中缺失的炮记录信息.
利用SRME分离抽稀数据的反射波及多次波记录,当炮间距过大时应当采用其他方法分离反射波与多次波(Liu et al., 2009, 2010; 薛亚茹等, 2012).将反射波及多次波记录抽到共检波点道集域,按检波器位置分别有1746个共检波点道集.
以位于15324 m处的第850个共检波点道集为例.为了方便与下文中的图片对比,抽出第850个共检波点道集的原始记录(图9a)在本文展示,图9b为该共检波点道集的反射波记录.炮间距为道间距的2倍, 表现为每隔一道有一个数值为0的空道,反射波记录的FK谱中出现空间假频(图9c).
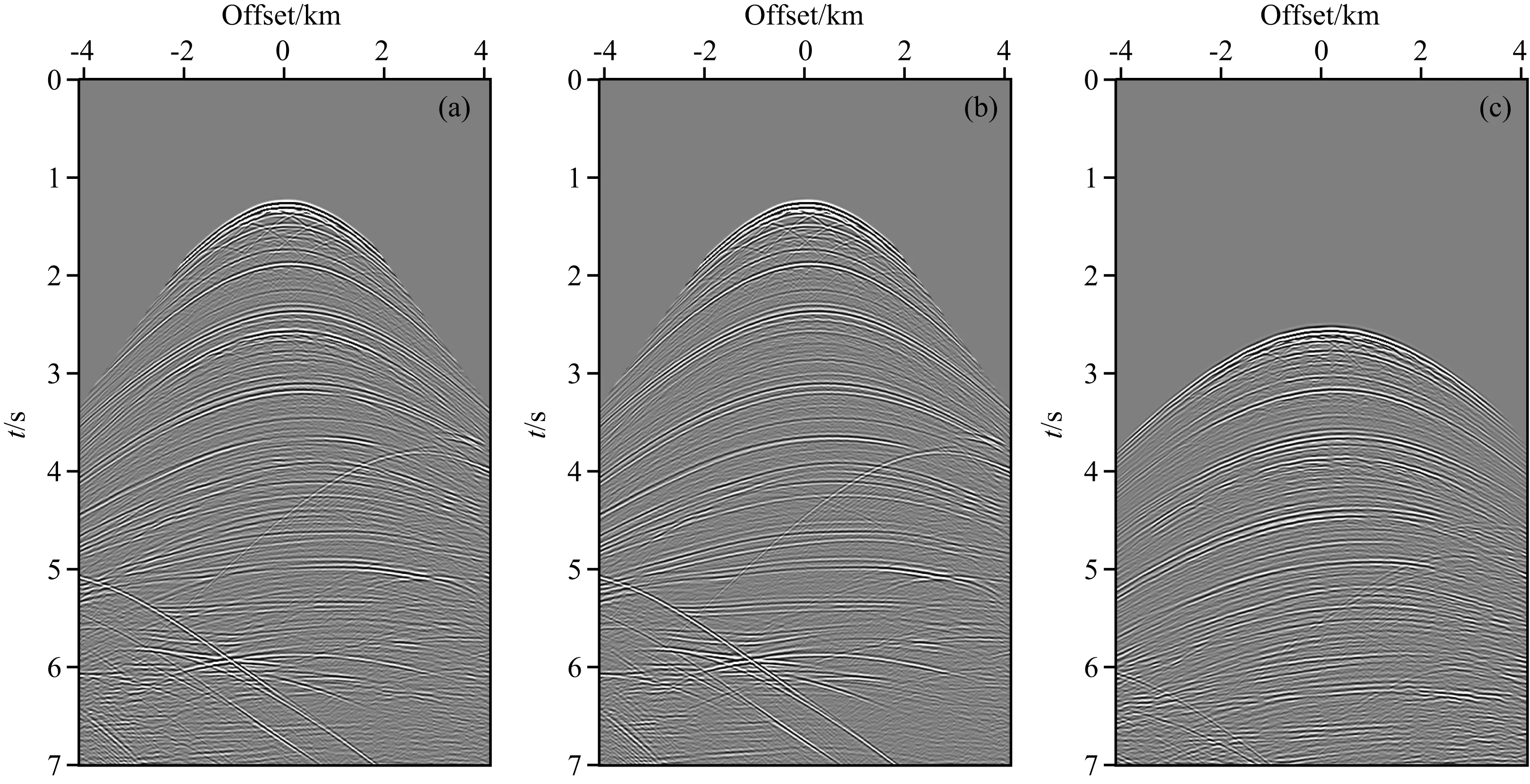
图6 原始炮集中第350炮的(a)原始记录; (b)反射波估计; (c)预测得到的多次波Fig.6 The 350th shot′s in original shot gather (a) Original wavefield record; b) Estimated primaries; (c) Predicted multiples
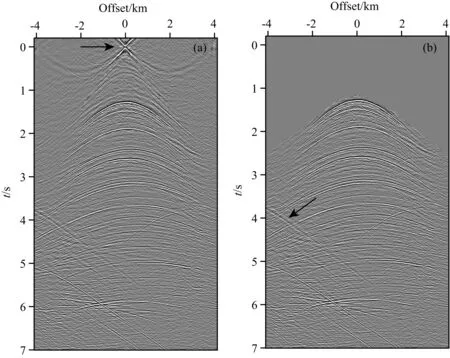
图7 (a)原始记录转换的波场记录; (b)切去图(a)中聚焦点周围的能量,得到多次波转换的波场记录Fig.7 (a)Wavefield record transformed from original record; (b) get wavefiled record transformed from multiples after muting energies around the focal point

图8 (a)多次波直接转换的波场记录; (b)消减图(a)中的多次波,得到一阶多次波转换的反射波Fig.8 (a) Wavefiled record transformed directly from multiples; (b) Primaries transformed from first-order multiples after subtracting multiples in figure(a)
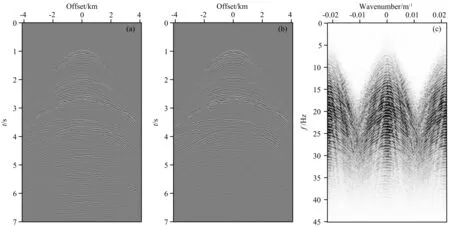
图9 抽稀原始炮集, 即将偶数炮充零并将奇数炮保留.然后在共炮域利用SRME分离反射波和多次波.将数据从共炮域整理到共检波点道集域.图中展示了抽稀数据第850个共检波点道集的(a)原始记录和(b)反射波记录;(c)图(b)中反射波的FK谱.Fig.9 Extract the original shot gather to be sparseness, i.e., fill the even number shots with zero and retain the odd number shots. And then, we separate primaries and multiples with SRME in the common shot domain. Rearrange data from common shot domain into common receiver domain. For the sparse data, the 850 th common receiver gather′s (a) Primaries and (b) Multiples are displayed in this figure; (c) Primaries′ FK spectrum in figure(b).
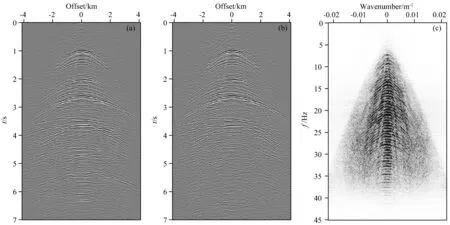
图10 在共检波点道集域,对多次波直接做局部聚焦变换(a) 多次波转换的波场记录,原始炮集中缺失的炮记录信息得到还原; (b) 减去图(a)中的多次波,得到一阶多次波转换的反射波记录; (c) 图(b)中反射波的FK谱.Fig.10 In the common receiver domain, do the local focal transformation directly with multiples(a) Wavefield record transformed from multiples, the information of missing shot records in original gather is retrieved; (b) Primaries transformed from first-order multiples got after subtracting multiples in figure(a); (c) Primaries′ FK spectrum in figure(b).

图11 将一阶多次波在共检波点道集域转换的反射波抽回到共炮域(a)抽稀炮集的反射波记录;(b)一阶多次波转换的反射波记录,原始炮集中缺失的炮记录信息得到还原.图中从左到右依次为第350、351、352、353炮.Fig.11 Rearrange primaries transformed from first order multiples in common receiver gather domain back into common shot domain(a)Primaries of shot gather extracted to be sparseness; (b)Primaries transformed from first order multiples, the information of missing shot record in original gather is retrieved. The 350th、351th、352th、353th shot are displayed from left to right.
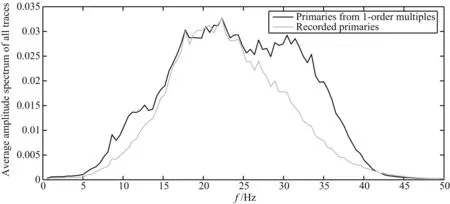
图12 灰白色与黑色曲线分别为图11a、图11b中第351炮反射波的平均振幅谱.两条曲线被调整为有相同的最大值Fig.12 The gray and black curves are respectively average amplitude spectrums of 351th shots′ primaries in Fig.11a and Fig.11b. The maximum value of two curves are scaled to be identity

图13 抽稀炮集中反射波的(如图11a)逆时偏移剖面Fig.13 Reverse time migration section of primaries in shot gather extracted to be sparseness (as shown in Fig.11a)
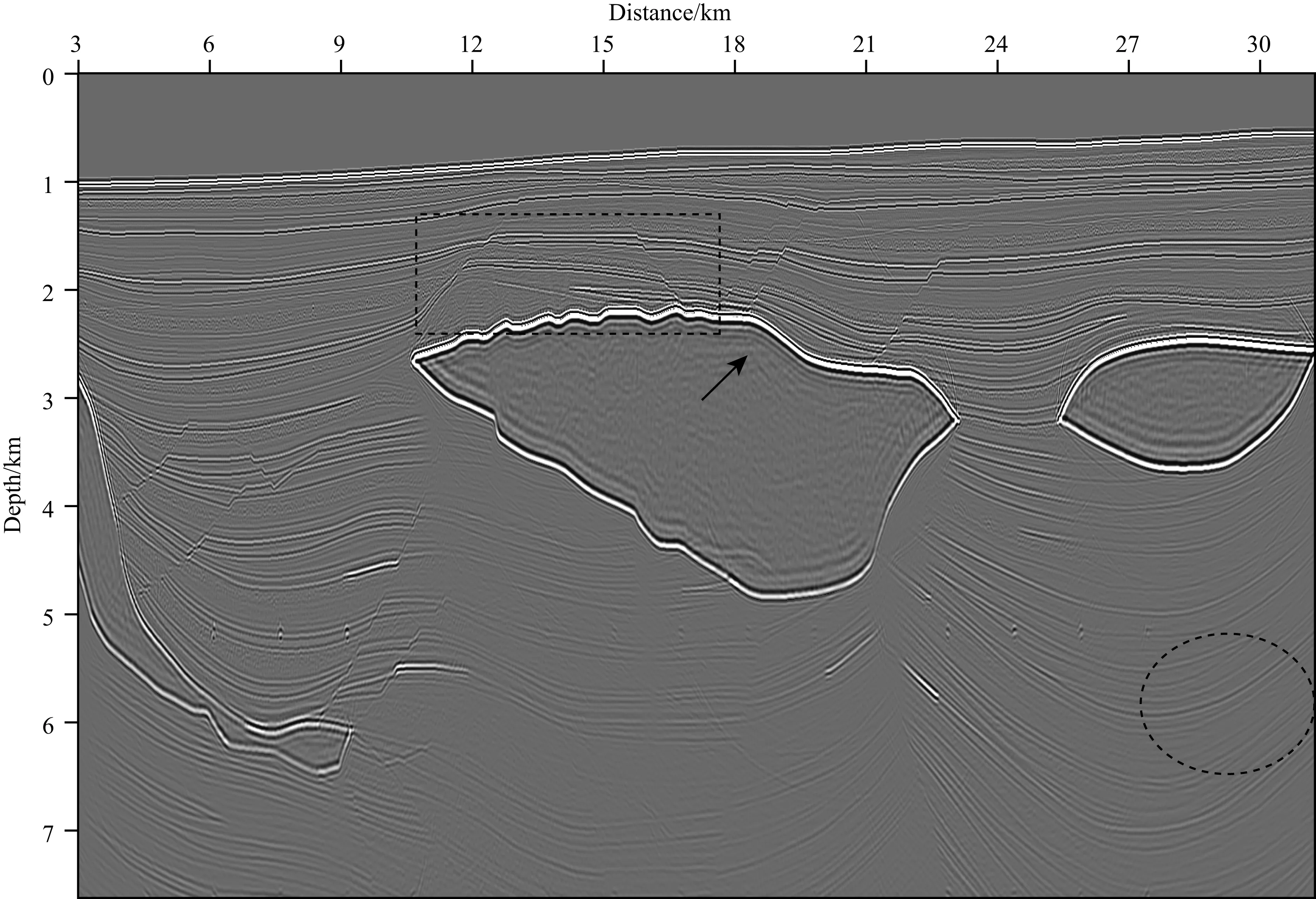
图14 一阶多次波转换的反射波(如图11b)的逆时偏移剖面其有更均衡的能量分布、相对较高的纵向分辨率和局部更高的信噪比.Fig.14 Reverse time migration section of primaries transformed from first order multiples (as shown in Fig.11b), which has more balance energy distribution, relatively higher vertical resolution and locally has higher signal-to-noise ratio
直接对第850个共检波点道集的多次波ΛMr850做局部聚焦变换(公式(20)),首先要将该道集覆盖范围内的所有共检波点道集的反射波估计按位置逐列存储到矩阵ΛΔPr850中.从多次波中还原得到炮间距与道间距相同的新波场记录(图10a).将新波场记录中高阶多次波转换的多次波减去,得到一阶多次波转换的反射波(图10b).转换反射波的FK谱如图10c所示,其中没有空间假频.
原始抽稀炮集的反射波记录如图11a所示,将转换的反射波记录从共道集域(如图10b)抽回到共炮域如图11b所示.对比两图可知:从多次波还原得到了炮点采样频率与检波点采样频率相同的新波场记录,提供比原始记录更丰富的叠前偏移信息.从图12的振幅谱分析中可以看出,一阶多次波转换的反射波有比原始反射波更宽的频带范围;由于聚焦变换的去子波效应,一阶多次波转换的反射波比原始反射波有更高的纵向分辨率.
原始反射波、转换反射波的逆时偏移结果分别如图13、图14所示,转换反射波的逆时偏移成像即为一阶多次波的聚焦变换逆时偏移成像.逆时偏移的成像条件是互相关成像条件;原始反射波逆时偏移的震源子波为15Hz雷克子波;为了与如图12所示的振幅谱分析吻合,转换反射波逆时偏移的震源子波采用20Hz雷克子波.对比图13和图14可知,一阶多次波聚焦变换成像的优势体现在: 1)纵向分辨率更高,尤其在剖面的浅层,剖面能量整体分布更为均衡;2)在局部有更高的信噪比(如矩形虚线所圈位置)及更好的偏移噪声压制(如箭头所指位置以及椭圆虚线所圈位置).
一阶多次波成像剖面往往与传统反射波成像剖面有近似的有效信息和不同的构造假象,并在局部表现出更好的成像效果.因此: 1)一阶多次波成像剖面可以成为反射波成像剖面解释工作中的有益参考; 2)寻找使反射波成像剖面与一阶多次波成像剖面最佳匹配的局部滤波器,压制反射波成像剖面中的噪声.此外,一阶多次波成像提供了比传统反射波成像更丰富的小角度信息,可以为速度分析作出贡献.
4 结论
本文叙述了聚焦变换的基本原理,并提出局部聚焦变换;理论上证明炮点比检波点稀疏时,共检波点道集域的局部聚焦变换可以将多次波准确转换成炮点与检波点有相同采样频率的新波场记录;数值算例很好地验证了上述理论.由于聚焦变换的去子波效应,在两个数值实验中,我们都可以看到多次波转换的新波场记录比原始波场记录有更高的纵向分辨率.在第二个数值算例中,相比原始反射波成像,一阶多次波聚焦变换成像的能量更为均衡、在局部表现出更好的偏移噪声压制和更高的信噪比、以及较高的纵向分辨率.通过理论分析和数值试验可以看出,多次波完全可以做为有效信号,提供更高的下地表覆盖次数,对成像做出贡献.
致谢 感谢匿名审稿专家提出的宝贵意见.作者感谢国家自然科学基金项目、国家油气重大专项以及中国科学院战略性先导科技专项(B类)资助的联合资助.
Baysal E, Kosloff D D, Sherwood J W C. 1983. Reverse time migration.Geophysics, 48(11): 1514-1524, doi: 10.1190/1.1441434.
Berkhout A J. 1993. Migration of multiple reflections. ∥63th Ann. Mtg. and Intl. Expo., Soc. Expl. Geophys.. Expanded Abstracts, 1022-1025.Berkhout A J, Verschuur D J. 1994. Multiple technology: Part 2, migration of multiple reflections. ∥64th Ann. Internat. Mtg., Soc. Expl. Geophys.. Expanded Abstracts, 1497-1500. Berkhout A J, Verschuur D J. 1997. Estimation of multiple scattering by iterative inversion, Part I: Theoretical considerations.Geophysics, 62(5): 1586-1595, doi: 10.1190/1.1444261. Berkhout A J, Verschuur D J. 2003. Transformation of multiples into primary Reflections. ∥73rd Ann. Internat. Mtg., Soc. Expl. Geophys.. Expanded Abstracts, 1925-1928. Berkhout A J, Verschuur D J. 2004. Imaging multiple reflections, the concept. 74th Ann. Internat. Mtg., Soc. Expl. Geophys.. Expanded Abstracts, 1273-1276.
Berkhout A J, Verschuur D J. 2006. Imaging of multiple reflections.Geophysics, 71(4): SI209-SI220, doi: 10.1190/1.2215359.
Claerbout J F. 1968. Synthesis of a layered medium from its acoustic transmission response.Geophysics, 33(2): 264-269, doi: 10.1190/1.1439927.
Guitton A. 2002. Shot-profile migration of multiple reflections. ∥72nd Ann. Internat. Mtg., Soc. Expl. Geophys.. Expanded Abstracts, 1296-1299.
He R Q, Hornby B, Schuster G T. 2007. 3D wave-equation interferometric migration of VSP free-surface multiples.Geophysics, 72(5): S195-S203, doi: 10.1190/1.2743375. Hu H, Liu Y K, Chang X, et al. 2013. Analysis and application of boundary treatment for the computation of reverse-time migration.ChineseJ.Geophys. (in Chinese), 56(6): 2033-2042, doi: 10.6038/cjg20130624. Jiang Z Y, Sheng J M, Yu J H, et al. 2007. Migration methods for imaging different-order multiples.Geophys.Prospect., 55(1): 1-19, doi: 10.1190/1.2370257.
Li P, Liu Y K, Chang X, et al. 2007. Application of the equipoise pseudomultichannel matching filter in multiple elimination using wave equation method.ChineseJ.Geophys. (in Chinese), 50(6): 1844-1853.
Liu Y K, Jin D G, Chang X, et al. 2009. Multiple subtraction using statistically estimated inverse wavelets. ∥79th Ann. Internat. Mtg., Soc. Expl. Geophys.. Expanded Abstracts, 3098-3102.
Liu Y K, Jin D G, Chang X, et al. 2010. Multiple subtraction using statistically estimated inverse wavelets.Geophysics, 75(6): WB247-WB254, doi: 10.1190/1.3494082.
Liu Y K, Chang X. 2011a. Reverse time migration of multiples. ∥81th Ann. Internat. Mtg., Soc. Expl. Geophys.. Expanded Abstracts, 3326-3331.
Liu Y K, Chang X, Jin D G, et al. 2011b. Reverse time migration of multiples for subsalt imaging.Geophysics, 76(5): WB209-WB216, doi: 10.1190/1.3627888.
Lu S P, Whitmore N D, Valenciano A A et al. 2011. Imaging of primaries and multiples with 3D SEAM Synthetic. ∥81th Ann. Internat. Mtg., Soc. Expl. Geophys.. Expanded Abstracts, 3217-3221.
Manuel C D, Uren N F. 2001. Migration Velocity analysis using seismic multiples. ∥ASEG 15th Geophysical Conference and Exhibition, 1-4.
Muijs R, Robertsson J O A, Holliger K. 2007. Prestack depth migration of primary and surface-related multiple reflections: Part II—Identification and removal of residual multiples.Geophysics, 72(2): S71-S76, doi: 10.1190/1.2424544.
Schuster G T, Yu J, Sheng J, et al. 2004. Interferometric/daylight seismic imaging.Geophys.J.Int, 157(2): 838-852, doi: 10.1111/j.1365-246X.2004.02251.x.
Schuster G. 2008. Seismic Interferometry. Cambridge University Press.
Sheng J. 2001. Migrating multiples and primaries in CDP data by crosscorrelogram Migration. ∥71th Ann. Internat. Mtg., Soc. Expl. Geophys.. Expanded Abstracts, 1297-1300.
van Groenestijn G V, Verschuur D J. 2006. Reconstruction of missing data from multiples using the focal transform. ∥76th Ann. Internat. Mtg., Soc. Expl. Geophys.. Expanded Abstracts, 2737-2741.Vasconcelos I, Snieder R, Hornby B. 2008. Imaging internal multiples from subsalt VSP data—Examples of target-oriented interferometry.Geophysics, 73(4): S157-S168, doi: 10.1190/1.2944168.
Verschuur D J, Berkhout A J, Wapenaar C P A. 1992. Adaptive surface-related multiple elimination.Geophysics, 57(9): 1166-1177, doi: 10.1190/1.1443330.
Verschuur D J, Berkhout A J. 1997. Estimation of multiple scattering by iterative inversion; Part II, Practical aspects and
examples.Geophysics, 62(5): 1596-1611, doi: 10.1190/1.1444262.
Verschuur D J, Berkhout A J. 2005. Transforming multiples into Primaries: experience with field data. ∥75th Ann. Internat. Mtg., Soc. Expl. Geophys.. Expanded Abstracts, 2103-2106.
Wang Y B, Chang X, Hu H. 2014. Simultaneous reverse time migration of primaries and free-surface related multiples without multiple prediction.Geophysics, 79(1): S1-S9, doi: 10.1190/geo2012-0450.1.
Wapenaar K, Fokkema J. 2006. Green′s function representations for seismic interferometry.Geophysics, 71(4): SI33-SI46, doi: 10.1190/1.2213955.
Xue Y R, Chen X H, Ma J T. 2012. Multiples attenuation based on directional orthogonal polynomial transform.ChineseJ.Geophys. (in Chinese), 55(10): 3450-3458, doi: 10.6038/j.issn.0001-5733.2012.10.028.
附中文参考文献
胡昊, 刘伊克, 常旭等. 2013. 逆时偏移计算中的边界处理分析及应用. 地球物理学报, 56(6): 2033-2042, doi: 10.6038/cjg20130624.
李鹏, 刘伊克, 常旭等. 2007. 均衡逆多道匹配滤波法在波动方程法压制多次波中的应用. 地球物理学报, 50(6): 1844-1853.
薛亚茹, 陈小宏, 马继涛. 2012. 多方向正交多项式变换压制多次波. 地球物理学报, 55(10): 3450-3458, doi: 10.6038/j.issn.0001-5733.2012.10.028.
(本文编辑 汪海英)
Focal transformation imaging of first-order multiples
LIU Xue-Jian1,2, LIU Yi-Ke1, HU Hao1,2, XIE Song-Lei3
1KeyLaboratoryofEngineeringGeomechanics,InstituteofGeologyandGeophysics,ChineseAcademyofSciences,Beijing100029,China2UniversityofChineseAcademyofSciences,Beijing100049,China3SouthChinaSeaInstituteofOceanology,ChineseAcademyofSciences,Guangzhou510301,China
Surface-related multiples penetrate into the subsurface several times and contain abundant reflection information of small angles. Compared with primaries, they sometimes can provide higher fold and better illumination for subsurface. Instead of trashing multiples as noises during the seismic data processing, nowadays, a lot of methods have been proposed to image multiples. Conventional migration methods have been modified for directly imaging multiples, e.g., Kirchhoff migration of multiples, wave equation migration of multiples, or reverse-time migration (RTM) of multiples. Alternatively, the linear two-step procedures can be utilized for imaging multiples. Primaries can be extracted from multiples based on seismic interferometry or focal transformation, and then imaged by utilizing conventional migration methods. However, most methods for imaging multiples would generate so many artifacts due to the undesired interactions between seismic-events (i.e. primaries and different-order multiples), which are hard to be attenuated and seriously pollute the true-image. Moreover, the least-squares based focal transformation can transform first-order multiples into primaries, second-order multiples into first-order multiples, etc., with few noises generated. Multiples focal-transformed from higher-order multiples can be eliminated by surface-related multiples elimination (SRME). And then, primaries focal-transformed from first-order multiples can be imaged by any conventional migration methods, and we call the procedures focal transformation imaging of first-order multiples.The focal transformation is proposed by Berkhout and Verschuur, which is developed from SRME. Primaries are once subsurface response of sources, surface-related multiples include different-orders, and the raw data contain primaries and surface-related multiples. Focal transformation is manipulated with several matrices that contain the full data of mono-frequency, one column stores one shot gather or one common-receiver gather. Primaries need to be estimated prior to focal transformation, and the inverse of primaries matrix is used as focal operator. The full raw data will be transformed into the new wavefield records. In fact, the focal transformation is implemented with a stable form of least-squares sense. Primaries are focused around one point in the profile of zero-time and zero-offset, the so called focal-point; first-order multiples are transformed into primaries; second-order multiples are transformed into first-order multiples; etc. Focal transformation is a kind of least-squares transformation, which nearly doesn't generate noises. So, after muting the energies around focal point, SRME can be utilized to eliminate the multiples transformed from higher-order multiples, and transformed primaries are obtained. Alternatively, in order to utilize the information of multiples, we can directly implement the focal transformation of multiples that usually have been separated from primaries during the regular seismic data processing, and the muting work can be avoided. On the other hand, the focal transformation has the effect of deconvolution by utilizing the inverse of real source-signature matrix, so the transformed primaries have higher vertical resolution than the acquired primaries. However, when the receive array moves with the source position, the matrices will occupy large memory that are mostly wasted by off diagonal 0 elements. In this article, we put forward two improvements for focal transformation: (1) develop the local focal transformation for reducing storage and computation; (2) bring in the weighted matrix, and demonstrating that local focal transformation in common-receiver domain can transform multiples into new wavefield records retrieving the missing shot-gathers of acquired data. The local transformation is implemented specially for one shot gather or one common-receiver gather, so the local focal transformation has better adaptation to the acquired data whose traces move with corresponding source position. We introduce the diagonal matrix into the focal transformation. When source sampling rate is sparser than receiver sampling rate of acquired data and one column of the matrices stores one common-receiver gather, the diagonal elements of the weighted matrix are periodically 1 spaced by 0 diagonal elements. The focal transformation transforms multiples into new wavefield records where source sampling is the same with receiver sampling, when the source sampling is sparser than receiver sampling in the acquired data. The local focal transformation in common-receiver domain also can transform multiples into new wavefild records with denser source sampling, but the common-receiver gathers must be extracted from shot-gathers in advance.In the first numerical test, two workflows of local focal transformation of row data and direct local focal transformation of predicted multiples are compared. They are both implemented in common-shot domain. We verify the second work flow will generate wavefield records with higher signal to noise ratio, and the laborious task for muting the energies around focal point is avoided. With the first workflow, a few parts of primaries are not focused around the focal point and leaked into the profile transformed from multiples. With the second workflow, the new wavefiled records directly transformed from multiples nearly do not have noises, and multiples transformed from higher multiples can be successfully eliminated by SRME. Obviously, the wavefield records transformed from multiples have higher vertical resolution than the acquired data. The second numerical test demonstratesthat when source sampling is relatively sparse, the local focal transformation in common-receiver domain can effectively transform first-order multiples into primaries; the transformed primaries include the missing shot-gathers of the acquired data; the imaging result of transformed primaries is more balanced, locally has higher signal-to-noise ratio, and shows slightly higher vertical resolution. The separated primaries and multiples are both rearranged into common-receiver gathers in advance; the zero traces in common-receiver gathers show the missing shot records; that every other trace in common-receiver gathers are zero represents the sparse source sampling, and alias artifacts can be clearly seen in the FK domain. The direct local transformation of multiples on common-receiver gathers can retrieve the missing shot records from multiples, and the alias artifacts in the FK domain are avoided. In the common-receiver domain, multiples transformed from higher-order multiples are eliminated by SRME, and the transformed primaries are rearranged back into the common-shot domain. The transformed primaries have wider amplitude spectrum than acquired primaries, which demonstrate focal transformation has the effect of deconvolution. The transformed primaries and acquired primaries are both migrated by RTM.The focal transformation can transform first-order multiples into primaries with few noises, and it has the effect of deconvolution. The proposed local focal transformation is implemented specially for one shot or one common-receiver gather, so the local focal transformation can save computation and storage. The local focal transformation in common-receiver domain can retrieve the missing shot records of acquired data from multiples. When source sampling of acquired data is sparse, the RTM image of primaries transformed from first-order multiples is more balanced, locally has higher signal-to-noise ratio, and shows slightly higher vertical resolution.
Focal transformation; Imaging of multiples; Multiples elimination
10.6038/cjg20150614.
国家自然科学基金项目(41374138),国家油气重大专项(2011ZX05008-006)和中国科学院战略性先导科技专项(B类)(XDB01020300)联合资助.
刘学建,男,1987年生,在读博士研究生,从事表面多次波消除、多次波成像方法以及最小二乘逆时偏移等方面的研究. E-mail:liuxuejian10@mails.ucas.ac.cn
10.6038/cjg20150614
P631
2014-05-08,2015-05-08收修定稿
刘学建,刘伊克,胡昊等. 2015. 一阶多次波聚焦变换成像.地球物理学报,58(6):1985-1997,
Liu X J, Liu Y K, Hu H, et al. 2015. Focal transformation imaging of first-order multiples.ChineseJ.Geophys. (in Chinese),58(6):1985-1997,doi:10.6038/cjg20150614.
