基于模块化多电平变换器的负序电流补偿系统研究

2015-02-18陈耀军陈柏超秦振杰赖向东

电源学报 2015年6期

关键词：正序负序三相

陈耀军，陈柏超，秦振杰，赖向东

（1.空军预警学院黄陂士官学校，武汉4300345；2.武汉大学电气工程学院，武汉430072）

基于模块化多电平变换器的负序电流补偿系统研究

陈耀军1，陈柏超2，秦振杰1，赖向东1

（1.空军预警学院黄陂士官学校，武汉4300345；2.武汉大学电气工程学院，武汉430072）

针对三相负载不平衡引起的负序电流，提出了基于模块化多电平变换器 MMC（modular multilevel converter）进行补偿的方案，讨论了其工作特性，提出了相应的控制策略。首先，通过把三相不平衡负载等效为平衡负载的方法，推导出对补偿系统控制的基本要求，明确了补偿的基本原理；然后，分析了补偿系统输入功率特性，提出了MMC用于负序补偿时的等效模型，并分析了环流及电容电压的波动特性，指出三相电容电压之和必定存在二次谐波波动；引入正负序坐标系分离控制的控制策略；最后通过仿真和实验验证了文中提出的结论和控制策略。

负序电流；模块化多电平变换器；等效模型；正负序电流分离

引言

随着现代经济社会的发展，电网用户端负载越来越复杂，特别是高速铁路的飞速发展，给电网供电稳定和供电设备带来了影响。由于高铁供电一般采用单相供电，对电网来说，三相负载不平衡，给系统带来严重的负序电流问题。因此治理负序电流问题是高铁供电的一个重要问题［1］，为此，科研人员付出了大量的努力，取得了显著的成果［2－5］。但从电网端看，负序电流问题仍然存在，影响着设备安全。由于电网电压等级高，传统的拓扑结构无法满足需求。

2003年，Marquardt和Lesnicar提出了模块化多电平变换器MMC（modular multilevel converter）的拓扑结构［6］，其具有模块化的结构，易于实现冗余，可以获得多电平，甚至无谐波输出，和电网可以通过标准变压器或直接相连，非常适合于中高压应用场合，获得了广泛的关注［7－11］。如果将这种变换器用到电网输电变电站进行集中补偿，则不仅可以补偿系统的负序电流，还可以起到潮流控制、稳定电压的作用。虽然这种变换器模块数量众多，整体成本较高，但其使用可以减少甚至取消对高铁供电变电站负序补偿设备的要求，从整体上看提高了应用效益。文献［12］提出了基于MMC的负序补偿策略，其把负序电流和谐波电流一起作为污染电流进行补偿，其基本方法为得到所需的补偿电流指令后，通过比例控制来输出所需的补偿电流，显然比例控制无法获得零误差，针对不同的补偿电流，其控制参数也难以优化，而且也没有分析进行负序电流补偿时系统的一般特性。

本文以基于MMC的负序电流补偿系统为研究对象，研究其一般性的原理及控制策略。首先把不对称负载的供电系统等效为对称负载、不对称电源的供电系统，提出负序补偿所需的控制形式，分析了补偿系统的输入功率特性、MMC的环流及电容电压波动情况；并把针对输入交流电压不平衡的PWM整流器的正负序分离控制策略引入到负序电流补偿中，采用信号延时对消法来分离正负序电流［13］，实现了正序和负序变量的独立控制；最后通过仿真和实验验证了文中的结论和控制策略。

1 负序电流补偿系统基本结构及原理

基于MMC的负序补偿系统简化原理如图1所示。图中，iu、iv、iw为系统电流，iLu、iLv和iLw为三相负载电流，iru、irv和irw为三相MMC电流（MMC的结构及工作原理详见文献［6－12，14］），Ls为线路等效电感，Z1、Z2和Z3为三相负载。图中三相电压源是对称的，而三相负载不对称，这就会带来负序电流，通过MMC的补偿作用，使三相电源的输出电流是对称的正序电流。

如果系统不加补偿，定义a=ej120°，有。则系统电流的正序分量和负序分量可以表示为

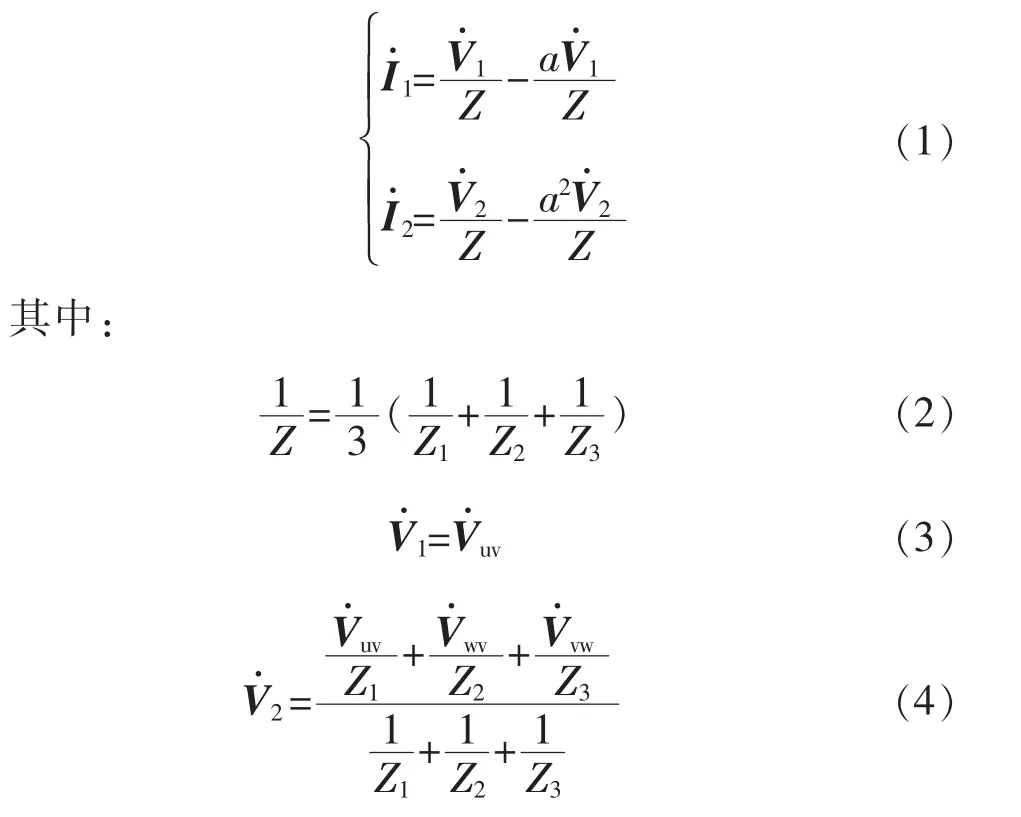
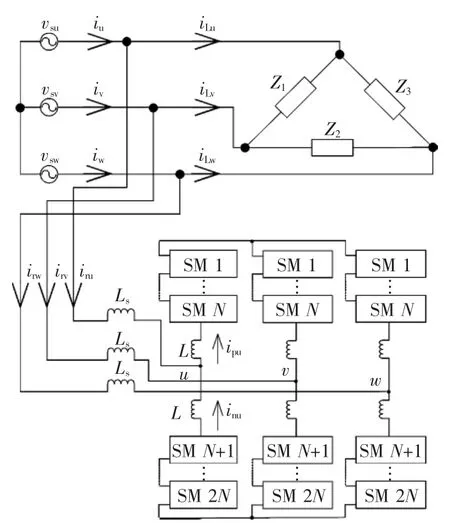
图1 基于MMC的负序补偿系统结构Fig.1 Negative currents compensation system constructure based on MMC

由于系统电流为正序电流和负序电流之和，因此，不加补偿时系统等效如图2所示。图中

从图2中可以看出，原系统中不对称负载变成了对称的负载，而供电电源为一组正序电压源和一组负序电压源的串联，补偿系统并联在正序电源和负序电源之间。如果用电压源的方式进行负序补偿，则要求补偿系统能够同时控制正序输出电压和负序输出电压。考虑到正序系统和负序系统的独立性，在进行负序补偿时，可以将系统控制分为正序控制和负序控制。

图3所示为系统正序控制和负序控制等效矢量，图中，Xr为补偿系统和电网等效连接阻抗。图3（a）为正序控制框图，通过补偿系统调节其输出电压的幅值和相位来控制电流的幅值和相位，从而保证补偿系统电容电压稳定以及功率的需求。图3（b）为负序控制框图，负序电流只取决于控制电压Vr2和连接阻抗Xr，调节Vr2，使和相等，这样就可以保证为0，补偿了负序电流。由此可见，要补偿系统负序电流，需要补偿系统同时输出正序电压和负序电压，正序电压是整个补偿系统稳定工作的需要，而负序电压用于补偿负序电流。

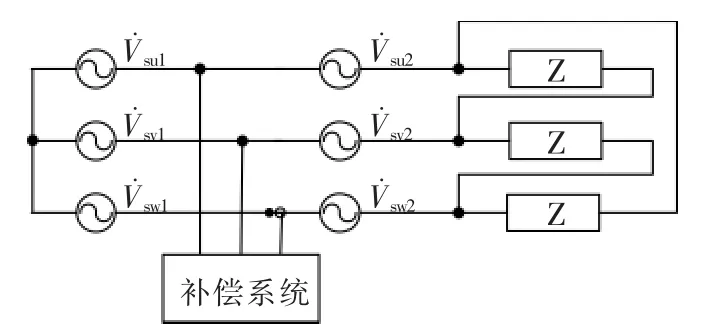
图2 负序电流产生等效原理Fig.2 Equivalent principle of negative currents generation

图3 负序补偿等效矢量Fig.3 Equipment vector of negative currents compensation

2 补偿系统输入功率特性

稳态时，如果MMC只进行负序电流补偿，且不考虑有功损耗，则MMC输出电流只为负序电流。假设电网电压的幅值和相位分别为Vs和φv，MMC输出电流的幅值和相位分别为Ir2和φri2。

考虑到电网电压是正序的，MMC电流是负序的，可以推导出MMC三相总有功功率为

可见，三相总瞬时有功功率不是一个恒定的值，而是一个2倍基波频率的变量，其周期平均值为0。如果不考虑损耗，负序补偿是不耗能的。则每相的周期平均有功功率分别为

从式（6）可以看出，虽然三相总周期平均有功功率为0，但每相有功功率不可能同时为0，至少有两相不为0。也就是说，在负序补偿过程中，必然存在有功功率转移的过程，即从一相或两相向另外两相或一相转移，补偿系统本身只是一个功率转移的载体，如果忽略自身损耗，其是不耗能的。

根据传统意义上的无功功率定义，无功功率可以表示为

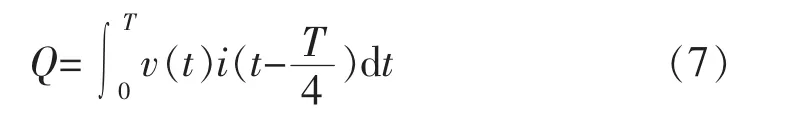
式中，T为基波周期。则每相无功功率及三相总无功功率Qs可以分别表示为

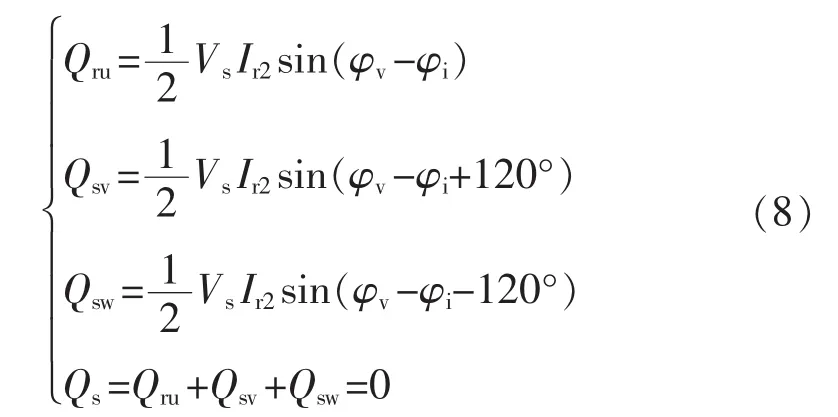
显然，三相总的无功功率为0，但三相无功功率中，至少有两相不为0，也就是说，无功功率也在相间转移流动。

可见，无论何种情况，进行负序电流补偿时，在三相之间必然存在着有功功率和无功功率的流动，负序补偿的实质是有功功率和无功功率在三相间重新分配的过程，补偿系统在此担任的是功率转移的角色。补偿系统总体不耗能（忽略损耗），但其总瞬时功率却不为0，而是一个2倍基波频率的变量。

3 MMC环流及电容电压波动分析

文献［14］提出了MMC的一种状态方程以及相应的等效模型，根据本文的参考方向，该状态方程可以修改为

D为微分算子；Z=diag［LdcLacCdcCac］；x=［iZuiuvdcvac］；u=［VovuN］T。其中，Cdc＝2CΣ；Cac＝8CΣ；CΣ＝C/N；vdc=（vΣPu+vΣNu）/2；vdc=（vΣPu-vΣNu）/4；vΣPu和vΣNu分别为上下桥臂模块电容电压之和；iZu为u相环流，iu为u相输出电流；Rdc＝2rd，Ldc＝2L，Rac＝rd/2＋Rs，Lac＝L/2＋Ls。

根据式（9），负序补偿时的三相模型如图4所示。由图可以看出，系统可以分为交流侧和直流侧，电容Cdc反映了一相模块电容电压之和，而Cac则反映了上下桥臂点的电压之差。在进行负序补偿时，三相交流侧相对独立，而直流侧则并联在一起，相间的功率流动必定通过整流和逆变的方式在直流侧完成交换。

根据前面的分析可知，在负序补偿时，MMC输出的电压是正序电压和负序电压的叠加，那么其开关函数也可分为正序开关函数和负序开关函数，设其的值分别为S1、S2，初始相位为φru1和φru2。

定义图4中直流侧受控电流电流源为

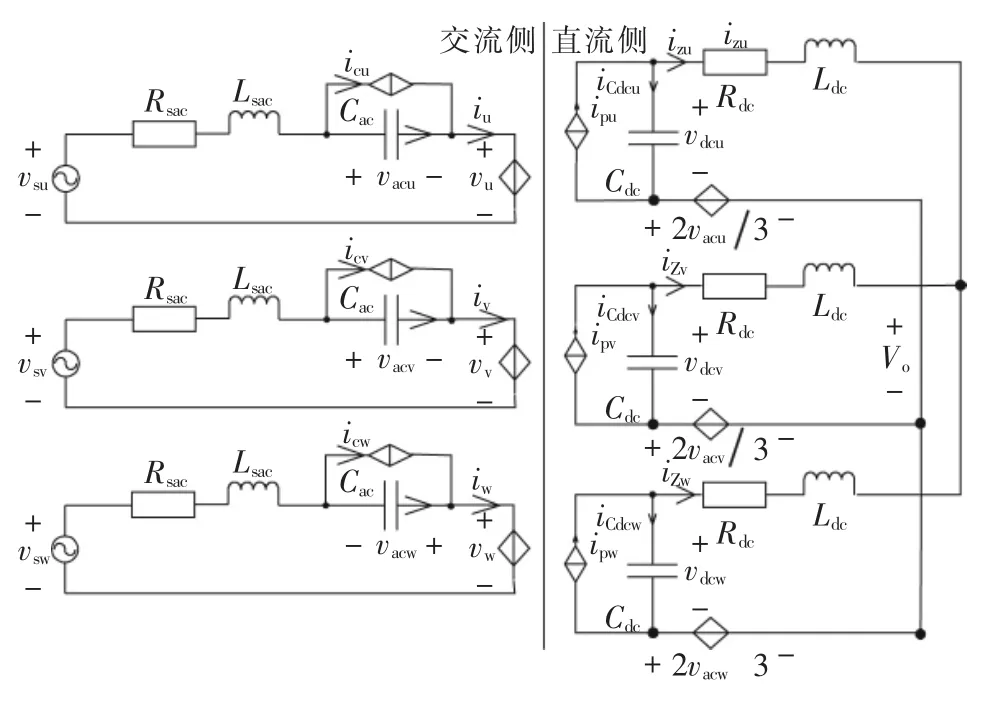
图4 MMC负序补偿等效模型Fig.4 Equivalent model of MMC with compensation for negative currents

式中，ipu1、ipv1、ipw1和ipu2、ipv2，ipw2分别为正序调制函数和负序调制函数引起的电流，根据式（9）可以分别推导出其表达式，即

从图3（b）可见，负序补偿电流的产生回路只有Xr和Vr2，如果忽略等效电阻，则Xr为纯感抗或容抗，这样产生的负序补偿电流Ir2必然和控制电压Vr2正交，即Ir2和Vr2正交。因此，式（12）中的直流分量必然为0，于是，式（12）可以写成

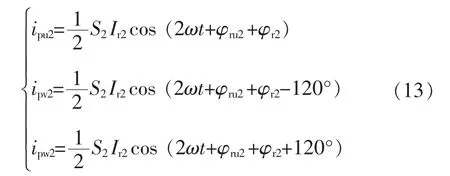
从式（13）可以看出，负序电流通过负序调制函数，给直流侧电容引入了正序电流，这会引起电容电压的二次谐波波动，但由于电流的正序特性，三相电容电压的二次谐波之和为0。显然，电容电压的二次谐波会给三相环流iZu，iZv和iZw带来正序电流，于此同时，流过负序电流的电容Cac产生的负序电压会通过正序调制函数在直流侧产生正序二次谐波电流。因此，系统直流侧电流，即环流的二次谐波呈正序特性，并取决于输入负序电流及正序调制函数。

式（11）则表达了负序电流通过正序调制函数后给直流侧电容引入的电流，其交流成分为零序二次谐波电流，直流成分则反映了有功功率的流动。显然，直流有功从一相或两相向另外两相或一相转移。综合前述的关于输入功率特性的分析，可以得出：在负序电流的补偿过程，一相或两相的有功功率通过整流变成了直流有功功率，并通过另外两相或一相逆变反馈给电网。因此，基于电压源型的负序电流补偿变换系统，在进行负序补偿时，三相之间必然存在着有功交换，即有功环流。由于式（11）中的交流成分是三相零序电流，而在直流侧的零序阻抗为电容Cdc，因此三相零序电流会在三相电容中产生零序电压，但不会在环流中形成零序电流。考虑到式（11）引起的电容电压波动，可以发现，三相电容电压波动幅值是有差异的，而三相电容电压波动和为

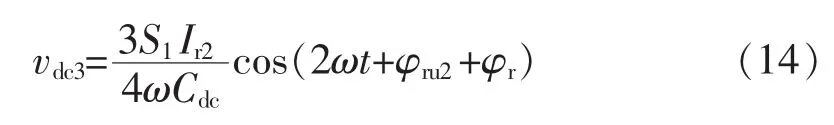
因此，在负序补偿时，总的电容电压不是纯直流，而是存在着二次谐波，其幅值正比于负序电流幅值和正序调制函数幅值。

根据式（11），三相环流可以表示为

式中，iZ2和φZ2分别为环流二次谐波的幅值和相位，其大小取决于输出负序电流以及正序调制函数。可以看出，环流中存在二次谐波，并呈现正序特性；三相环流的直流成分体现了该相的功率传输特性，直流环流大于0表明该相在吸收功率，直流环流小于0表明该相输出功率；三相直流环流之和为0。

4 基于正负序坐标系的分离控制策略

由前面分析可以看出，MMC要补偿系统的负序电流，必须产生一个正序电压和一个负序电压。如果能将系统变量分为独立的正序分量和负序分量，则可通过坐标变换把正序和负序分量分别变换到正序和负序坐标系中，这样正序和负序分量在各自的坐标系中表现为直流特性，通过正序控制器和负序控制器使系统正序和负序分量得到独立控制。

如果把系统电流直接进行正序和负序坐标变换，则负序电流在正序坐标系中表现为二次谐波特性，而正序电流在负序坐标系中表现为二次谐波特性，这不利于系统控制。可见，要完成正序和负序坐标系中的独立控制，必须对系统变量进行正负序分离，一般有3种方法来解决这个问题，①在坐标变换后插入低通滤波器，滤掉二次谐波分量，但这会带来较大的延时；②在坐标变换后插入二次谐波陷波器，只滤除二次谐波，对其他分量影响较小，因而可以获得较好的性能，但陷波器设计相对较复杂；③采用信号延时对消法［13］，这是一种稳态和动态性能均比较优越的算法，且容易实现，算法的实现框图如图5所示。三相变量经过坐标变换后到αβ两相静止坐标系中，其αβ分量经过1/4周期延时后和当前的值进行交叉加减运算，在αβ两相静止坐标系中就可以实现正序分量和负序分量的分离。分离后的变量经过重组后，通过坐标变换，把正序分量和负序分量分别变换到正向旋转坐标系和反向旋转坐标系中，二者均表现为直流特性，消除了正负序分量在dq坐标系中的相互影响。

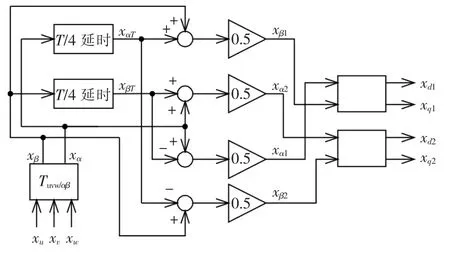
图5 信号延时对消法实现框图Fig.5 Applicable diagram of delay signal cancellation method

在旋转坐标系中，实现了正序和负序分量的分离后，就可以在各自的坐标系中完成各自的控制目标，系统控制框图如图6所示。图中，控制系统分为正序控制和负序控制两部分，正序控制用于稳定电容电压，以电容电压为控制目标，采用电压电流双闭环控制。分析表明，三相输出电容电压的平均值含有二次谐波分量，因此电容电压反馈需经LPF滤波，去掉其交流成分，电压外环控制器的输出即为有功电流内环指令。电流内环采用常规的解耦控制策略，其输出为正序调制函数的dq分量，经过坐标变换，变换成三相正序调制函数，用于控制MMC的正序电流，从而完成电容电压的控制。

三相负载电流经过正负序分量分离及变换后，其负序dq分量用作负序电流控制的给定，MMC输出负序电流dq分量和其比较后，进行负序电流控制，其控制策略和正序电流控制器相同，其输出为负序调制函数的dq分量，经过坐标变换后变成三相负序调制函数，和正向调制函数相加，得到正负序控制所需的三相调制函数，调制策略采用载波重叠PWM［15］，从而使MMC输出负序电流和负载负序电流相等，这样就使三相电源输出电流达到平衡，全部为正序电流。

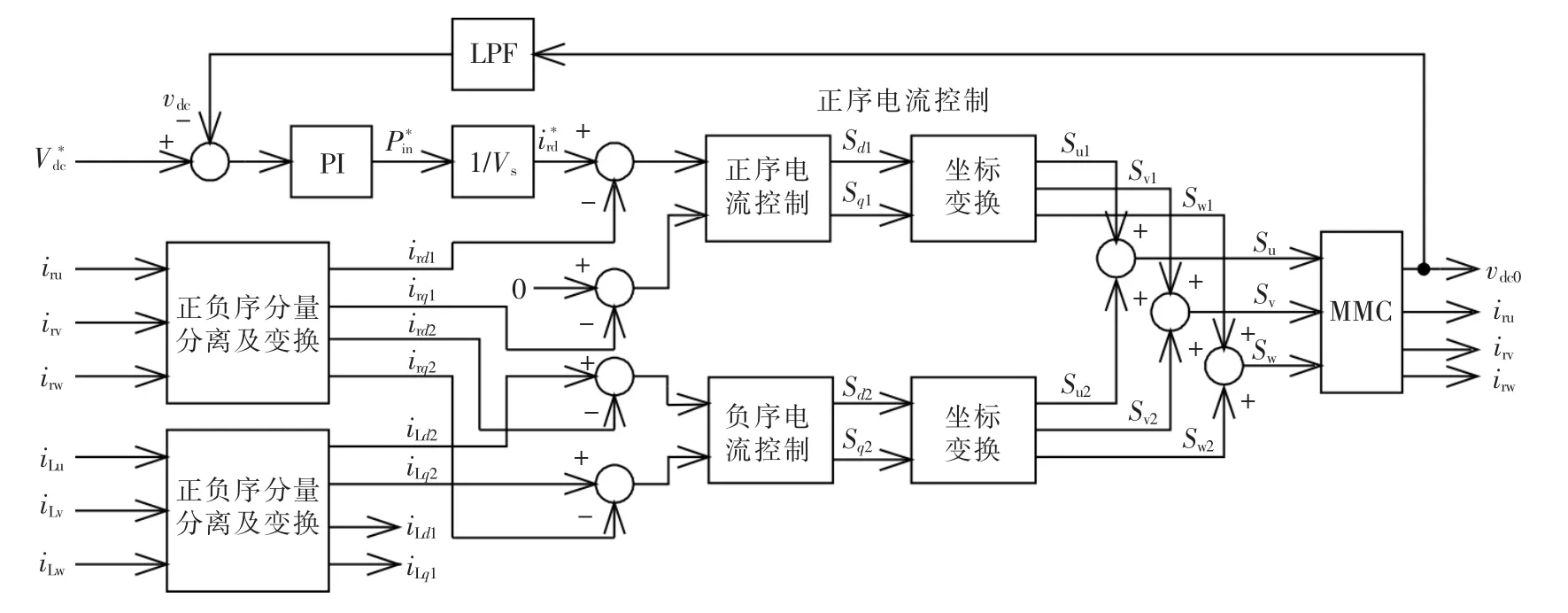
图6 负序补偿系统控制框图Fig.6 Control block diagram of negative currents compensation system

5 仿真及实验验证

5.1 仿真研究

为验证MMC进行负序补偿时的控制及工作特性，搭建了仿真平台。仿真参数如下：三相交流电压源的线电压有效值为110 kV，变压器及线路等效电感Ls为15 mH，在uw相之间连接一电感LL和电阻RL组成的负载，LL为200 mH，RL为280 Ω，v相不接负载，则v相负载电流为0，这样三相负载电流不平衡，产生负序电流。在仿真时，从0.6 s开始进行负序补偿，但MMC始终进行电容电压稳定控制。MMC主要仿真平台参数如表1所示。

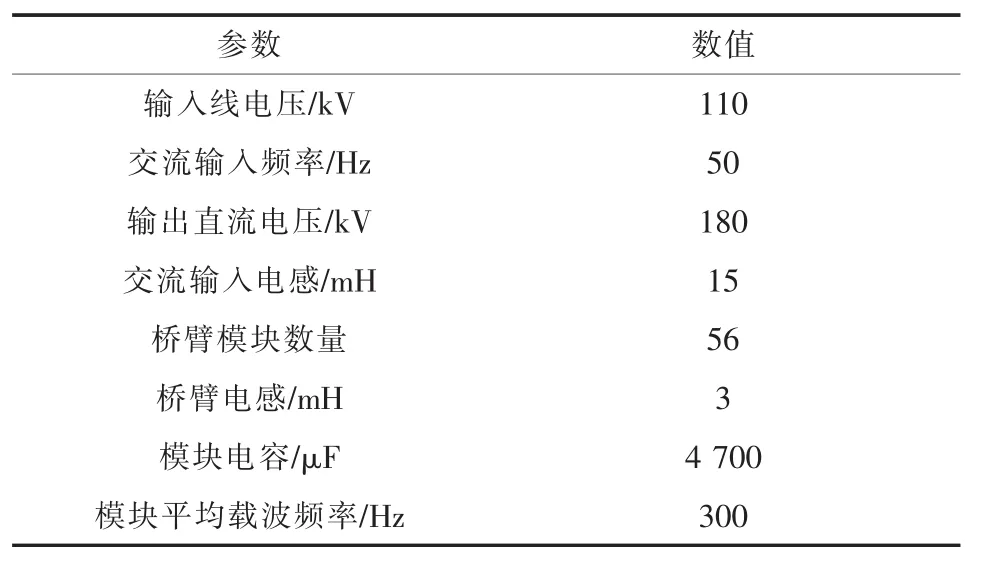
表1 仿真平台参数Table.1 Parameters of simulation platform

图7所示为三相系统输出电流仿真波形。在0.6 s以前，系统没有进行负序补偿，MMC只进行电容电压稳定控制，此时系统电流为负载电流，isu和isw幅值相同，相位相反，isv基本为0，这个很小的值是MMC损耗而引起的正序有功电流。在0.6 s以后，系统突然进行负序补偿，经过几个周期的调整后，系统输出平衡的正序三相电流，负载负序电流得到了有效的补偿。补偿后的三相电流幅值约为原来两相电流幅值的0.577。

图7 三相系统电流仿真波形Fig.7 Simulation waveforms of three-phase system currents

图8所示为MMC输入电流仿真波形。在0.6 s前，只有很小的正序有功电流，用于补偿系统损耗。在0.6 s后，输出负序电流（叠加很小的正序分量），该电流和负载电流相加，就得到了补偿后的系统输出电流。MMC输出负序电流的大小完全取决于负载产生的负序电流大小。

图8 三相MMC电流仿真波形Fig.8 Simulation waveforms of thee-phase currents of MMC

图9所示为三相直流电容Cdc的电压vdc的仿真波形，可以发现在进行补偿控制后，三相电容电压vdc的平均值被稳定在180 kV，但含有二次谐波，这与前面的分析是一致的。三相电容电压vdcu、vdcv和vdcw的平均值和波动幅值均有一定的差异。因为直流电容电压除了受到桥臂等效电阻影响外，还要受到交流电容Cac的影响，因此，虽然三相电压平均值被控制到给定值，但三相电容各自的电压存在着差异。

图9 三相电容电压vdc仿真波形Fig.9 Waveforms of vdcof three-phase capacitor voltages

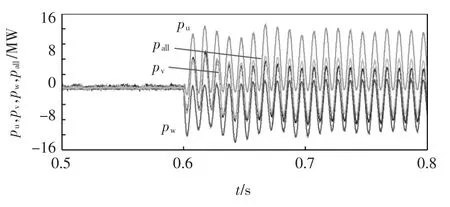
图10 MMC三相输入有功功率仿真波形Fig.10 Waveforms of three-phase input active power of MMC

图10为MMC交流输入的瞬时有功功率仿真波形，其通过输入电压和输入电流直接相乘得到。三相平均功率pall为三相功率直接相加除以3的结果，其是一个含有二次谐波的平均值为正的直流，这正的直流为MMC功率损耗。pu和pw的平均值小于0，pv的平均值大于0，表明u相和w相吸收功率，而v相释放功率。

图11为MMC交流输入的瞬时无功功率仿真波形。其是先将输入电压移相90°，然后再和输入电流相乘。qall的波形是一个包含二次谐波的波形，其平均值为0。qu平均值小于0，qv和qw平均值大于0，这表明，在补偿的过程中三相之间存在着传统意义上的无功功率转移的现象。

图11 MMC三相输入无功功率仿真波形Fig.11 Simulation waveforms of three phases input reactive power of MMC

图13所示为稳态时的实验波形。图13（a）所示为补偿前交流电源的输出电流波形，此时MMC处于不控整流状态。此时v相的电流为0，u相和w相的电流幅值相同，方向相反。图13（b）为补偿后的系统输出电流波形，电流为基本平衡的正序电流。图13（c）所示为MMC输出电流，其主要为负序电流，同时叠加有系统损耗引起的正序电流。图13（d）为MMC的三相输出相电压波形，其是一个5电平的波形，三相电压以正序为主，同时含有少量的负序分量，正序电压用于维持MMC电容电压的稳定，负序电压用于产生电流，从图3（b）可以推导出产生负序电流所需的负序电压。

图14为MMC突然进行控制时的实验波形。MMC开始处于不控整流状态，然后突然进行正负同时控制。图14（a）所示为交流电源输出电流波形，可以看出，MMC刚进行控制时，系统v相电流迅速增大，三相电流基本平衡，但三相电流幅值都增大，主要原因是需要正序有功电流对MMC模块电容电压进行充电，使其达到给定值。

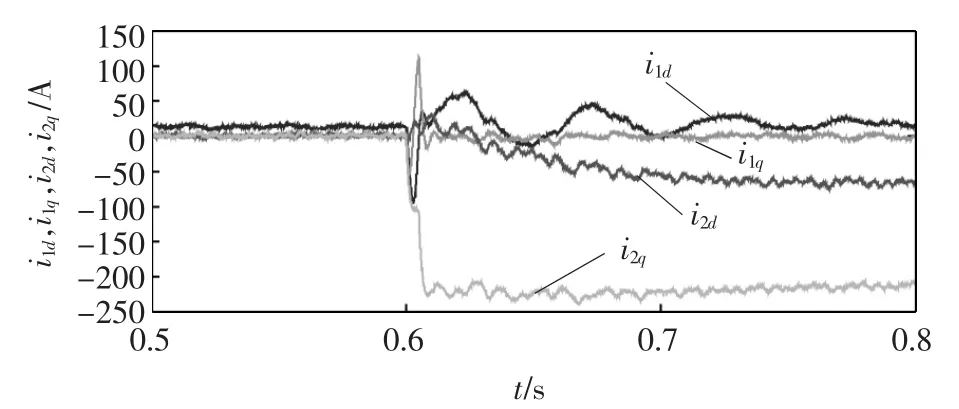
图12 MMC正序和负序电流dq坐标系中的仿真波形Fig.12 Simulation waveforms of positive and negative currents of MMC in dq coordinate reference

表2 实验主要参数Tab.2 Parameters of experiment

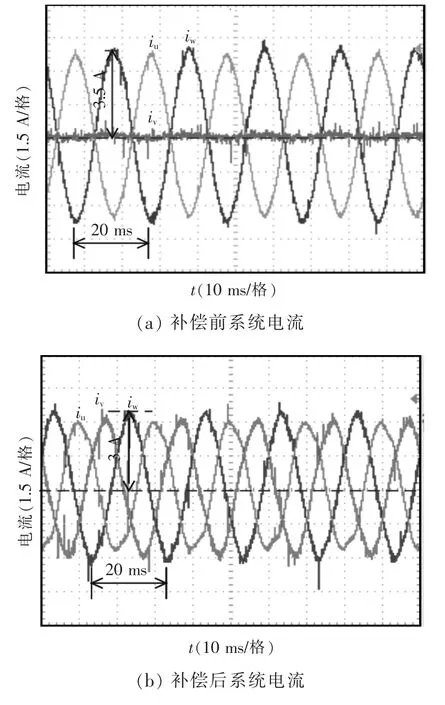
图13 稳态实验波形Fig.13 Experimental waveforms in stable state

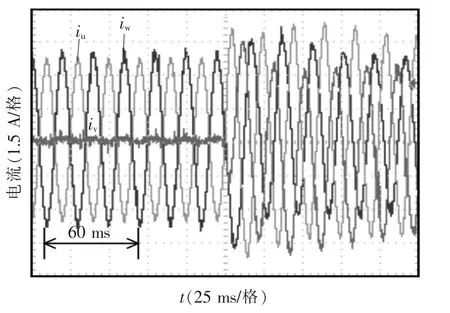
图14 突加控制时的实验波形Fig.14 Experimental waveforms when controlling suddenly

6 结语

本文研究了基于MMC的负序电流补偿系统的控制及工作特性。分析表明，补偿系统必须要提供一个正序电压和负序电压，以保证系统电容电压稳定及负序电流输出，负序电流补偿的过程实质是有功和无功从一相或两相通过直流侧转移给另外两相或一相转移的过程，三相电容电压平均值必然存在着二次谐波波动。本文引入延时信号对消法成功实现了系统正序和负序电流的分离，以此为基础实现了正序电流和负序电流的独立控制。仿真和实验结果证实了文中的结论和控制策略。

［1］Chen S L，Li R J，His P H.Traction system unbalance problem-analysis methodologies［J］.IEEE Transactions on Power Delivery，2004，19（4）：1877-1883.

［2］Mochinaga Y，Takeda M，Hasuike K.Static power conditioner using GTO converters for ac electric railway［C］.In Proc.Power Conversion Conference.Yokohama,Japan：1993：641－646.

［3］Shu Z L，Xie S F，Li Q Z.Single-phase back-to-back converter for active power balancing，reactive power compensation，and harmonic filtering in traction power system［J］.IEEE Transaction on Power Electronics，2011，26（2）：334－343.

［4］方璐，罗安，等.高速电气化铁路新型电能质量补偿系统［J］.电工技术学报，2010，25（12）：167－176.Fang Lu，Luo An，etc.A novel power quality compensator for high-speed electric railway［J］.Transactions of China Electrotechnical Society，2010，25（12）：167－176（in Chinese）.

［5］Luo An,Wu Chuanping,Shen Jhon,et al，Railway static power conditioners for high-speed train traction power supply systems using three-phase V/v transformers［J］.IEEE Transaction on Power Electronics,2011,26（10）:2844-2856.

［6］Lesnicar A，Marquardt R.An innovative modular multilevel converter topology suitable for a wide power range［C］.IEEE 2003 Power Tech Conference.Bologna，Italy，2003：23－26.

［7］Peng F Z，Qian Wei，Cao Dong.Recent advances in multilevel converter/inverter topologies and applications［C］// 2010 International Power Electronics Conference（IPEC）.Sapporo，Japan：IEEE，2010：492－501.

［8］王之赫，荆龙，吴学智，等.基于MMC的铁路功率调节器环流抑制策略［J］.电源学报，2014，12（6）：79－85.Wang Zhihe，Jing Ling，Wu Xuezhi，et al.Circulating current suppressing strategy of railway power static condition-er based on modular multilevel converter［J］.Journal of Power Supply，2014，12（6）：79－85（in Chinese）.

［9］杨云森，郭育华.单相模块化多电平变流器控制策略研究［J］.电源学报，2015，13（2）：88－93.Yang Yunsen，Guo Yuhua.Research on control strategy of single-phase MMC［J］.Journal of Power Supply，2015，13（2）：88－93（in Chinese）.

［10］思蕴，施科研，陈敏，等.模块化多电平变流器（MMC）两种调制比较［J］.电源学报，2013，11（3）：58－63.Wang Siyun，Shi Keyan，Chen Min，et al.Two control methods used in modular multilevel converter［J］.Journal of Power Supply，2013，11（3）：58－63（in Chinese）.

［11］范文宝，杨晓峰，王晓鹏，等.基于模块组合多电平变换器的SVG控制策略［J］.电工技术学报，2011，26（1）：29－35（in Chinese）.Fan Wenbao，Yang Xiaofeng，Wang Xiaopeng，et al.Control strategy SVG based on of modular multilevel converter［J］.Transactions of China Electrotechnical Society,2011,26（1）：29－35（in Chinese）.

［12］杨晓峰，范文宝，王晓鹏，等.基于模块组合多电平变换器的STATCOM及其控制［J］.电工技术学报，2011，26（8）：7－13.Yang Xiaofeng,Fan Wenbao,Wang Xiaopeng,et al.Static synchronous compensator based on modular multilevel converter based STATCOM and its control［J］.Transactions of China Electrotechnical Society，2011，26（8）：7－13（in Chinese）.

［13］J Svensson，M Bongiorno，A Sinnino.Practical implementation of delayed signal cancellation method for phase sequence separation［J］.IEEE Trans.on Power Delivery， 2007，22（1）：18－26.

［14］陈耀军，陈柏超，袁佳歆，等.模块化多电平逆变器电容电压及环流控制［J］.电工技术学报，2014，29（10）：166－174.Chen Yaojun,Chen Baichao,Yuan Jiaxin,et al.The control of capacitor voltages and circulating currents of the modular multilevel inverter［J］.Trans-actions of China Electrotechnical Society,2014,29（10）:166－174（in Chinese）.

［15］Makoto H，Ryo M，Hirofumi A.Control and analysis of the modular multilevel cascade converter based on double-star chopper-cells（MMCC-DSCC）［J］.IEEE Trans.Power Electron.，2011，26（6）：1649-1658.

［16］Siemaszko D，Antonopoulos A，Ilves K，et al.Evaluation of control and modulation methods for modular multilevel converters［C］.in Proc.IPEC，2010：746-753.

Study of Negative Current Compensation System Based on Modular Multilevel Converter

CHEN Yaojun1，CHEN Baichao2，QIN Zhenjie1，LAI Xiangdong1
（1.Huangpi NCO School of AFEWA,Wuhan 4300345，China；2.School of Electrical Engineering of Wuhan University，Wuhan 430072 China）

According to negative currents causing by imbalance loads，a compensation strategy based on the modular multilevel converter（MMC）is proposed in this paper.The system with imbalanced three-phase loads is equivalent to the one with balanced loads but imbalanced power supplies，which indicates the demand to the compensation system.The input power characteristics of the compensation system are analyzed，and the equivalent model of the MMC is presented，and using this model，the fluctuant of the module capacitors and the circulating currents are analyzed，which result there must be second harmonic in the average voltage of the three phase capacitors.And then，the control strategy with dependent positive and negative controller is proposed and the delay signal cancellation method is used to separate the positive and negative currents.Finally，the simulation and experiment results verify the conclusions and the validity of the mentioned control strategy.

negative current； modular multilevel converter； equivalent model；coordinate reference frame；department of the positive and negative currents