基于灵敏度法的三芯电缆线芯温度影响因素分析

王 鹏，刘 刚

(华南理工大学电力学院，广东 广州510640)

0 引言

电力电缆运行中线芯的温度是确定电力电缆是否达到载流量的依据［1-3］。而电缆载流量是电缆运行中受环境条件和负荷因素影响的重要动态运行参数，其重要性影响到输电线路的安全可靠、经济合理运行以及电缆寿命问题［4］。电缆的载流量偏大，会造成电缆线芯的工作温度超过容许值，从而会影响绝缘的寿命;载流量偏小，则电缆线芯铜材或铝材就不能得到充分的利用，导致不必要的浪费［5-6］。

目前，通过线芯温度推算电缆载流量的方法有多种，如IEC标准、热路法、模拟热荷法、有限元法和有限差分法等。IEC 60287标准是目前最被认可、应用最广的运用传热学原理计算电缆载流量的解析算法，许多学者提出来的热路模型都是在IEC标准提出来的热路模型上进行的改进［7］。但是根据IEC 60287系列标准规定，无法准确计算载流量，主要是因为实际运行中电缆线路的载流能力受到诸多因素的影响，而外部环境(主要包括环境温度和环境热阻)是影响载流量的主要因素之一［8-9］。

另外，国内外将灵敏度分析应用于单芯电缆的研究已经趋近成熟［10-11］，但是应用于三芯电缆的研究却还比较有限。本文以三芯电缆为研究对象，对影响电缆线芯温度的环境热阻和环境温度两个因素进行了局部灵敏度分析，并设计了10 kV交联聚乙烯三芯电缆土壤直埋、空气敷设两种条件下的阶跃电流温升试验，得到不同负荷电流下采集的电缆线芯温度试验数据，并以IEC 60287电缆稳态温升公式为基础，推导出环境温度和热阻对线芯温度影响的局部灵敏度公式。利用推导的灵敏度公式计算实验条件下环境温度和环境热阻对线芯温度影响的灵敏度系数，并总结出一定的规律。

1 基于热路法的三芯电缆线芯温度计算

由于中低压电缆型号多样，为了与实验相结合，本文以型号YJV22-8.7/10-3×240的配网三芯电缆为研究对象，其结构图如图1所示。

参考传热学中建立多层材料热路的做法，将相同热阻率的材料归结为一层热阻，其次根据三芯电缆的温度场分布特征，不同结构的边界在同一等温线上时可作为热路模型中的节点，可以得出如图2所示的热路模型［12-16］。

图1 三芯电缆结构示意图

图2 10 kV三芯电缆稳态热路模型

Qc为单个线芯电缆线芯及内屏蔽层产生的损耗，即Qc=I2R，I为电缆载流量(A);R为线芯交流电阻(Ω);Qd为单个线芯绝缘及绝缘屏蔽层的介质损耗;λ1为单个线芯金属套及屏蔽的损耗因素;λ2为单个线芯铠装层的损耗因素;θ1为电缆线芯温度(℃);θ2为绝缘外表面及金属屏蔽层温度(℃);θ3为铠装层温度(℃);θ4为电缆外护套表面温度(℃);θ0为环境温度;T1为单个线芯绝缘层热阻(K/W);T2为填充层及内护套热阻(K/W);T3为外护套热阻(K/W);T4为环境热阻(K/W)。

比拟电路中的节点电压法，根据图2列温差平衡方程:

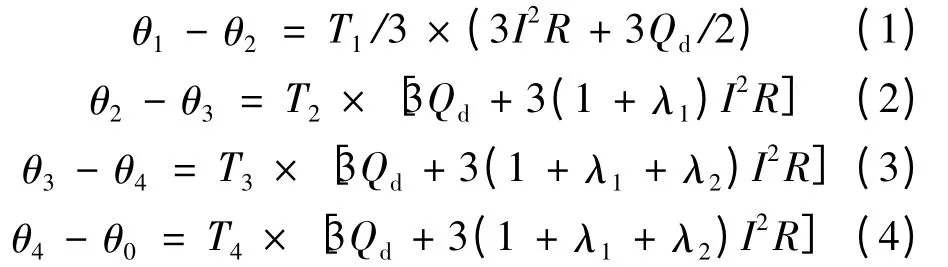
四式相加得三芯电缆线芯温度为:

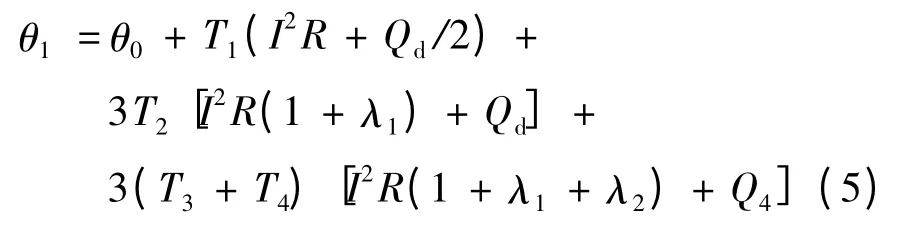
由于三芯电缆的线芯温度决定电缆载流量的大小，因此，θ1的变化可以表征电缆载流量的变化。根据式(5)可知，电缆的线芯温度由θ0、T4、R、Qd、λ1、λ2、T1、T2、T3这些参数共同决定，其中参数θ0、T4为外界环境参数，是变化量;参数R、Qd、λ1、λ2、T1、T2、T3为电缆本体的物理参数，是由电缆设计制造决定。因此，电缆线芯温度只与环境温度θ0和环境热阻T4有关。

2 环境热阻T4的计算

在10 kV三芯电缆的热路模型中，T4为电缆所处环境的热阻，根据IEC 60287可知［17-20］:

当空气敷设时，环境热阻T4为:

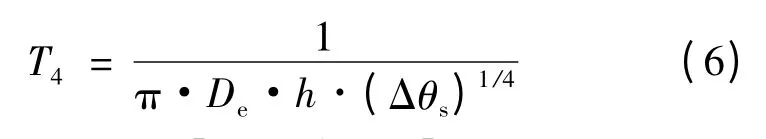
式中:h为传热系数［W/(m2·K)］;De为电缆外径(m);Δθs为电缆表皮温升(K)。

当土壤敷设时，环境热阻T4为:

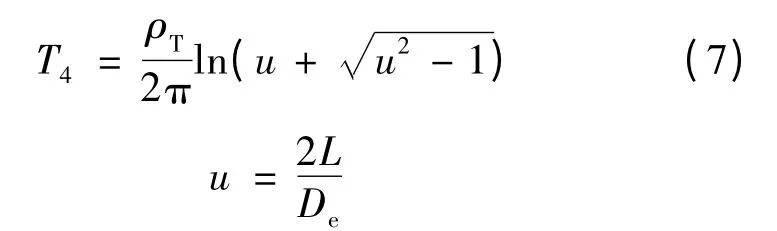
式中:ρT为土壤热阻系数(K·m/W);L为电缆轴线到地表的距离(m);De为电缆外径(m)。

3 T4和θ0的灵敏度分析

3.1 灵敏度定义

灵敏度分析是指反映模型中各种影响因子对模型结果的影响程度，其目的在于确定模型各参数对输出结果的影响大小，从而校正那些对模型输出结果影响较大的参数。灵敏度分析可以分为两种，即全局灵敏度分析和局部灵敏度分析［21］。

全局灵敏度分析是指，在模型中，多个参数的变化对模型结果产生的总的影响的分析，以及分析每个参数及参数之间的相互作用对模型结果的影响，也就是说在全局灵敏度分析中，每个参数在有限大或无限大的范围内变化时，由某个参数变化引起的模型结果的变化是全局的，即模型结果的变化是在所有参数变化的共同作用下产生的。

局部灵敏度分析是指，在模型中，单一参数变化时，对模型结果产生的影响，不考虑其他参数的影响，认为其他参数恒定不变。也就是说，当某个参数发生微小变化时，对模型的输出结果产生的变化程度，根据表征变化率的数学模型，灵敏度可用因变量(模型结果)对自变量(变化因子)的导数进行分析。

根据局部灵敏度的定义，网络参数T对某一参数X的灵敏度表示为［16］:

由于各变量的单位不同，需要进行归一化处理，得到网络参数T对某一参数X的归一化灵敏度为:

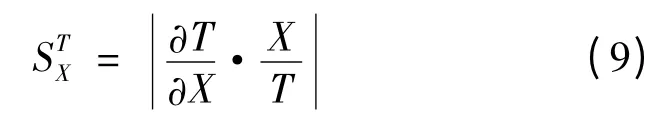
3.2 环境热阻T4对线芯温度θ1的灵敏度分析［22］

(1)当为空气敷设时

由于环境热阻T4与环境温度θ0有关，只考虑环境热阻对线芯温度的影响是不准确的，所以要考虑两个因素的影响。因此得到线芯温度θ1对环境热阻T4的归一化灵敏度为:

(2)当为土壤敷设时

由于土壤的环境热阻较大，环境温度基本保持不变，我们忽略环境温度的微小变化，仅考虑环境热阻对线芯温度的影响。得到土壤敷设时线芯温度对环境热阻的归一化灵敏度为:

3.3 环境温度θ0对线芯温度θ1的灵敏度分析

环境温度对线芯温度的影响主要考虑空气敷设时的情况，这是因为当电缆在土壤中敷设时，外部环境温度的变化非常微小，可以看做温度不变;而电缆在空气敷设时，根据有关文献可知，电缆外部环境温度在24 h中温差最大可达到6℃。

因此，在空气敷设时根据归一化灵敏度的定义，可知环境温度θ0对线芯温度θ1的归一化灵敏度为:

由灵敏度的物理意义可知，灵敏度越大越灵敏，参考文献［23］给出的参数灵敏度分级(如表1所示)，可将环境热阻与环境温度对线芯温度的灵敏度分类。

表1 参数灵敏度分级

4 实验研究与理论分析

4.1 实验方法与步骤

本实验系统可以分为两个部分，即为室内部分和室外部分。室内部分主要由调压器、升流器和实验电源组成，室外部分由实验电缆(型号YJV22-3×240)、自动测温仪组成，整个系统的电气接线如图3所示。

图3 10 kV三芯电缆升流试验原理图

对于三芯电缆来说，为了保证其内部每根线芯通过的电流相等，把三相线芯首尾相接，最终把A相和C相线芯的一端接至升流器的二次侧，具体接线如图4所示，如此则可保证实验电缆横截面温度场的对称性。

图4 三芯电缆接线原理图

然后，在空气敷设和土壤敷设条件下，在电缆表皮和线芯上分别敷设热电偶，测量不同加载电流下的电缆表皮温度和线芯温度的变化情况，对于土壤敷设，电缆埋深0.4 m。

最后，加载实验电流，分四种情况进行电流加载，这四种情况都为阶跃电流，从0 A直接加载到200 A、300 A、400 A、500 A，自动测温仪调节为每隔1 min记录一次数据。根据三芯电缆的热惯性，每种情况需要加载5 h，电缆线芯温度才能达到稳定，加载电流方式如图5所示。

4.2 实验结果与理论分析

针对10 kV三芯电缆，对其加载200 A、300 A、400 A、500 A四种不同的电流，并且在空气敷设和土壤敷设两种情况下，分别测量不同电流下达到稳态的电缆线芯温度和表皮温度，得到各种条件下的温度曲线，进而对其进行理论分析。

图5 电流加载方式图

4.2.1 两种不同敷设条件下的实验结果对比分析

图6～图9所示为在不同敷设条件下，加载200 A、300 A、400 A、500 A四种不同的电流时，电缆线芯温度和表皮温度随时间的变化趋势图。

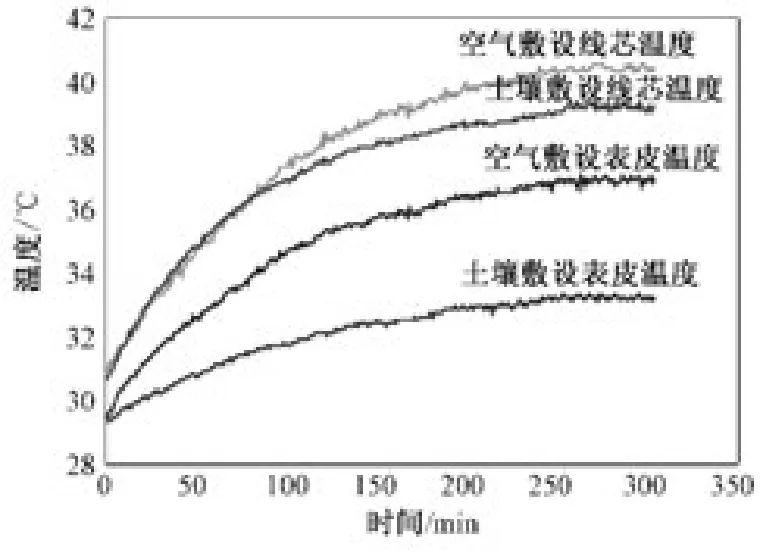
图6 200 A下三芯电缆线芯与表皮温度的实验值

图7 300 A下三芯电缆线芯与表皮温度的实验值

由图6～图9可知，在不同加载电流和不同敷设环境下，10 kV三芯电缆达到稳态时的线芯温度与表皮温度实验值见表2。

图8 400 A下三芯电缆线芯与表皮温度的实验值

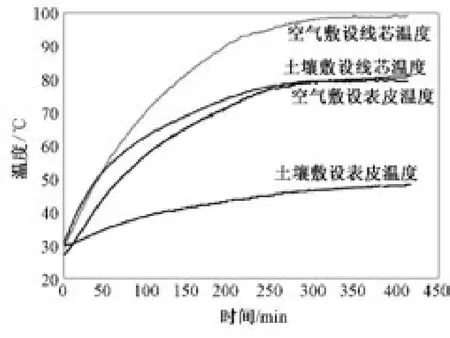
图9 500 A下三芯电缆线芯与表面温度的实验值

表2 10 kV三芯电缆达到稳态时线芯与表皮温度实验值

从表2可以看出，对于两种不同的敷设方式，当电缆加载200 A电流时，空气敷设时的电缆线芯温度比土壤敷设时的线芯温度约高1.4℃，空气敷设时的电缆表皮温度比土壤敷设时的表皮温度约高3.7℃;当电缆加载300 A电流时，空气敷设时的电缆线芯温度比土壤敷设时的线芯温度约高3.9℃，空气敷设时的电缆表皮温度比土壤敷设时的表皮温度约高8.4℃;当电缆加载400 A电流时，空气敷设时的电缆线芯温度比土壤敷设时的线芯温度约高5.4℃，空气敷设时的电缆表皮温度比土壤敷设时的表皮温度约高9.0℃;当电缆加载500 A电流时，空气敷设时的电缆线芯温度比土壤敷设时的线芯温度约高19.5℃，空气敷设时的电缆表皮温度比土壤敷设时的表皮温度约高32.9℃。

根据分析可知，电缆空气敷设时的稳态线芯温度与表皮温度都高于土壤敷设时的稳态线芯温度与表皮温度，这是因为在不同加载电流下，空气热阻都大于土壤热阻。由热阻的定义可知，热阻是热量在热流路径上遇到的阻力，反映介质或介质间传热能力的大小，因此空气敷设时的环境热阻较大，不利于热量的传递，导致电缆线芯温度与表皮温度较高，实验结果与理论计算相符合。

4.2.2 不同环境热阻下的实验结果分析

根据4.2.1中的分析可知，两种不同敷设情况下的电缆线芯温度差与表皮温度差随着加载电流的增大而增大，如图10所示为不同敷设情况下电缆线芯温度与表皮温度的相对差值对比图。

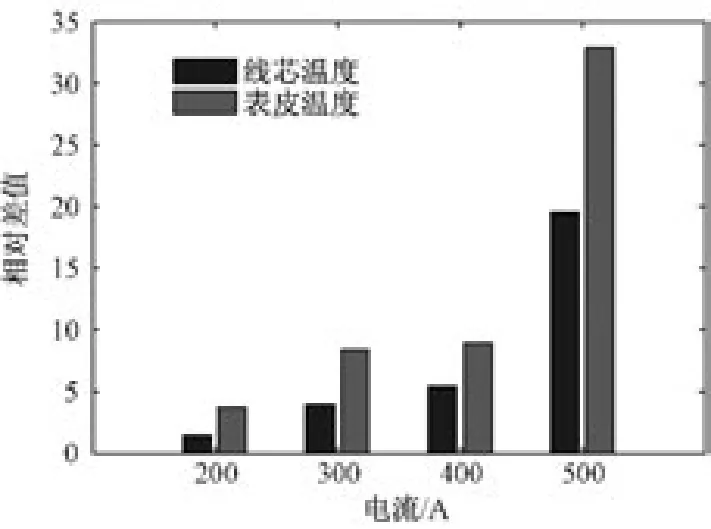
图10 空气敷设和土壤敷设的线芯温度与表皮温度差值对比图

从图10中可以看出，在两种不同敷设情况下，加载电流为200 A，电缆线芯稳态温度相等时，在环境热阻较小的土壤敷设下，载流量可以提高3.6%;加载电流为300 A，电缆线芯稳态温度相等时，在环境热阻较小的土壤敷设下，载流量可以提高8.1%;加载电流为400 A，电缆线芯稳态温度相等时，在环境热阻较小的土壤敷设下，载流量可以提高9.2%;加载电流为300 A，电缆线芯稳态温度相等时，在环境热阻较小的土壤敷设下，载流量可以提高22.3%。

从表3中可以看出，根据参数灵敏度分级表，在空气敷设情况下，加载电流为200A时=0.12＜0.2，为中度灵敏;加载电流为300 A、400 A、500 A时，=0.2，为灵敏，且500 A时的灵敏度最高，=0.6;在土壤敷设情况下，加载不同电流时＜0.05，为不灵敏。

对比不同敷设情况且在相同加载电流下的灵敏度可知，线芯温度的变化受到外部环境热阻变化的影响很大。根据实验所得的三芯电缆线芯与表面温度曲线图可知，外部环境热阻变化时，电缆线芯温度与表皮温度会产生较大变化，理论计算与实验结果相符合;在同一敷设情况下，随着加载电流的增大，外部环境热阻对线芯温度的灵敏度越来越大，图10中不同加载电流下线芯温度相对差值的变化趋势也证明了这一分析。

表3 两种不同敷设情况环境热阻T4对线芯温度θ1的灵敏度

4.2.3 不同环境温度下的实验结果分析

根据灵敏度计算公式可以得到表4中空气敷设下环境温度θ0对线芯温度θ1的灵敏度。由表4可知，随着加载电流的增大，环境温度θ0对线芯温度θ1的灵敏度逐渐变小，加载电流为200 A时最大，为0.8。因此，只需考虑加载电流为200 A时的情况，就可以得到电缆线芯温度随环境温度变化的关系，图11为加载电流200 A时的电缆线芯温度随环境温度变化趋势图。

表4 空气敷设下环境温度θ0对线芯温度θ1的灵敏度

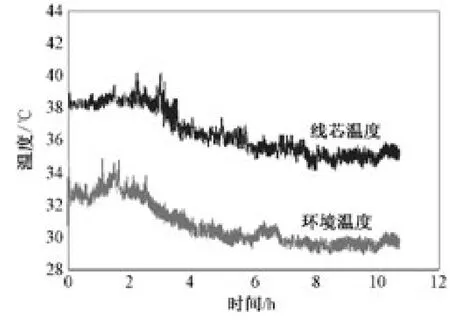
图11 200 A时的电缆线芯温度随环境温度变化趋势图

从图11可知，加载电流从0到200 A过程中，当三芯电缆运行状态未达到稳定时，电缆线芯温度是一个逐步升高的过程，这个过程中主导线芯温度的是加载电流的大小，且电缆线芯温度的变化也影响了电缆周围环境温度的变化;当三芯电缆运行状态达到稳定时，电缆线芯温度与敷设环境温度变化趋势趋于相同，且电缆线芯温度曲线稍微滞后于敷设环境温度曲线，说明敷设环境温度对电缆线芯温度的影响大，线芯温度主要由敷设环境温度决定，主要随敷设环境温度的变化而变化。

5 结论

为了研究三芯电缆载流量的影响因素，利用生物学中局部灵敏度的概念分析了环境热阻与环境温度对三芯电缆载流量影响的灵敏度系数，并且进行了不同加载电流下的10 kV三芯电缆温升实验，得到如下结论:

(1)两种不同敷设情况下的三芯电缆线芯温度差与表皮温度差随着加载电流的增大而增大。在空气敷设情况下，随着加载电流的增大，环境热阻对电缆线芯温度的灵敏度增加，且灵敏度都处于灵敏等级。在土壤敷设情况下，环境热阻对电缆线芯温度的灵敏度处于不灵敏等级。在同一加载电流下，外界环境热阻的变化对于电缆线芯温度的影响很大。

(2)在空气和土壤两种不同敷设情况下，当三芯电缆线芯温度相等时，加载电流为200 A，在土壤敷设下，载流量可以提高3.6%;加载电流为300 A，在土壤敷设下，载流量可以提高8.1%;加载电流为400 A，在土壤敷设下，载流量可以提高9.2%;加载电流为500 A，在土壤敷设下，载流量可以提高22.3%。可见，随着加载电流的增大，三芯电缆载流量可以提高的空间越来越大，间接地证明了结论(1)中空气敷设下灵敏度随加载电流的变化趋势，以及土壤敷设时的灵敏度分析。

(3)随着电缆加载电流的增大，环境温度对电缆线芯温度的灵敏度减小。当三芯电缆运行状态未达到稳定时，电缆线芯温度主要由加载电流的大小决定;当三芯电缆运行状态达到稳定时，电缆线芯温度的变化趋势与环境温度变化趋势基本相同，线芯温度由敷设环境温度决定。

［1］汤 毅，王晓并，陈燕萍，等.10 kV三芯交联电缆载流量的试验研究［J］.高电压技术，2009，35(11):2807-2812.

［2］郑雁翎.10 kV XLPE电力电缆稳态温度场和额定载流量的计算［J］.宝鸡文理学院学报，2009，29(2):59-62.

［3］高升宇，顾自强，王 震，等.XLPE电缆排管敷设时稳定载流量的理论计算［J］.电力设备，2007，9(8):6-11.

［4］游世宇，吴雨波，万 利，等.高压大电流下电缆附件电热老化实验装置的研制［J］.高压电器，2013，49(7):29-31.

［5］郭英军，孙丽华，梁永春，等.电缆热老化寿命的预测研究［J］.河北科技大学学报，2007，28(1):34-36.

［6］刘 刚，张高言，周 凡.基于等温松弛法的110 kV高压电缆老化状况评估［J］.高电压技术，2014，40(2):497-498.

［7］牛海清，王晓兵，张 尧.基于迭代法的单芯电缆载流量的研究［J］.高电压技术，2006，32(11):41-44.

［8］孟凡凤，张 兵，方晓明，等.影响直埋电缆载流量的因素的研究［J］.绝缘材料，2007，40(3):64-66.

［9］刘 刚，周 凡，黄旭锐.环境温度和环境热阻对单芯电缆导体温度计算灵敏度的影响分析［J］.广东电力，2012，25(10):51-54.

［10］刘 刚，雷成华.提高单芯电缆短时负荷载流量的试验分析［J］.高电压技术，2011，37(5):1288-1292.

［11］赖育庭，刘 刚，雷 鸣.基于热网络模型的电缆热场灵敏度分析方法［J］.南方电网技术，2011，5(2):51-54.

［12］杨世铭，陶文铨.传热学［M］.北京:高等教育出版社，2003.

［13］阴继翔.比拟法在传热学教学中的作用［J］.太原理工大学学报(社会科学版)，2001，19(3):64-66.

［14］李友荣，吴双应.传热学教学中的热路分析法［J］.高等建筑教育，2012，21(1):51-53.

［15］雷 鸣.依据表皮温度准确计算单芯高压电缆线芯温度的理论及实验研究［D］.华南理工大学，2011.

［16］胡倩楠.计算10kV三芯电缆导体温度的热路模型及应用研究［D］.华南理工大学，2013.

［17］IEC 60287－1－1:1994 Calculation of the current rating of electric cables，part 1:current rating equations(100% load factor)and calculation of losses，section 1:general［S］.

［18］IEC 60287－1－2:1993 Calculation of the current rating of electric cables，part 1:current rating equations(100% load factor)and calculation of losses，section2:sheath eddy current loss factor for two circuits in flat formation［S］.

［19］IEC 60287－2－1:1994 Calculation of the current rating of electric cables，part 2:thermal resistance，section 1:calculation of thermal resistance［S］.

［20］马国栋.电线电缆载流量［M］.北京:中国电力出版社，2003.

［21］许崇刚，胡远满，常 禹，等.生态模型的灵敏度分析［J］.应用生态学报，2004，15(6):1056-1062.

［22］刘 刚，雷成华.提高单芯电缆短时负荷载流量的试验分析［J］.高电压技术，2011，37(5):1288-1292.

［23］Lenhart L，Eckhard K，Fohrer N，et al.Comparison of two different approaches of sensitivity analysis［J］.Physics and Chemistry of the Earth，2002(27):645-654.