智能优化算法对提高分数阶算子的有理逼近精度研究
2015-02-18赵慧敏
徐 驰,赵慧敏,李 文
(1.大连交通大学 电气信息学院,辽宁 大连 116028;2.大连交通大学 软件学院,辽宁 大连 116028)*
0 引言
目前,分数阶控制理论的研究内容已经十分丰富,其中主要包括分数阶微积分算子的数值实现[1]、分数阶控制器设计[2]、分数阶系统辨识和分数阶控制系统的系统性能分析及其分析方法[3].在分数阶控制的诸多研究方向中,分数阶系统或算子模型的逼近方法研究是基础.由于分数阶微积分算子是复变量S的无理函数,要想对分数阶系统进行数值仿真和实际应用就必须对分数阶系统进行有理化近似.目前,在诸多分数阶算子有理化近似方法中,人们多采用Oustaloup间接离散化方法[4].该方法可以简单并且直观的根据参数计算公式来确定逼近传递函数,但是在所选定频率范围的低频与高频端的拟合效果不理想.实际上,当采用Oustaloup方法对分数阶算子进行有理逼近时,一旦确定了有理函数的结构即逼近阶次,那么根据参数计算公式可以发现逼近系数是对应于所选逼近频段与逼近阶次唯一确定的.因此要想在Oustaloup算法逼近频段与逼近阶次确定的基础上提高其有理逼近精度,可以从有理传递函数的系数着手,通过合理的改变有理传递函数的系数来提高其有理逼近精度.为此,本文在Oustaloup算法基础上采用粒子群优化算法对逼近传递函数的各系数进行寻优.在下面内容中,将对本文所提方法进行详细阐述,并通过具体实例进行有效对比,证明所提方法的有效性.
1 Oustaloup算法
Oustloup算法也叫信号滤波法,在实际情况下,大多数分数阶微分信号是无法预先知道的,那么我们可以通过构造滤波函数来实现对信号的数值处理.下面采用文献[4]给出的Oustaloup算法对分数阶微分算子进行有理逼近,得到有理传递函数:

这里选取拟合频段为[0.01,100]、逼近阶次为5.从式(1)可以看出分数阶微分算子Sα(α=0.5)的有理逼近函数H(s)的一般形式为:

从Oustaloup算法的定义式也很容易证明式(2).
2 粒子群优化(PSO)算法
Kennedy和Eberhart基于对鸟群运行模式的简化研究及行为模拟开发了一种优化算法—粒子群 优 化 算 法[5](Particle Swarm Optimization,PSO).文献[5]给出了粒子群优化算法的设计原理以及Matlab的相关程序实现.该算法的基本流程可归纳为:
Step1:在可行解空间内初始化所有微粒,包括在允许范围内的随机速度与位置.
Step2:评价每个微粒的位置适应值,计算其目标函数.
Step3:对于每个微粒,将其适应值与微粒自身所经历过的最好位置(pbest)进行比较,若更好,则将其替换为当前的pbest.
Step4:对于每个微粒,将其适应值与整个群体所经历过的最好位置(gbest)进行比较,若更好,则将其作为整个群体最优位置.
Step5:更新微粒的速度与位置.
Step6:若满足终止条件,则停止迭代,否则返回Step2.
3 PSO算法对提高分数阶算子有理逼近精度的研究
粒子群优化参数的选取包括粒子群初值、粒子群规模、惯性权重以及目标函数的确定:
(1)PSO初值的选取
因为所选逼近传递函数H(S)的阶次为5,则位置矢量选取 Xi=(b1,b2,b3,b4,b5),若要对分数阶微分算子S0.5进行有理逼近精度提高的研究,那么位置矢量的初始值 Xi0=(10,298.5,1 218,768.5,74.79),这样可以有效的避免 PSO 寻优的随机性,提高寻优效率.
(2)PSO惯性权重的选取
本文为了更好的平衡算法的全局搜索与局部搜索能力,采用线性递减惯性权重[6]

ωstart为初始惯性权重、ωend是迭代至最大次数时的惯性权重、k为当前寻优次数、Tmax为最大迭代次数.根据经验取 ωstart=0.9、ωsend=0.4、Tmax=300、微粒群规模m取30.
(3)目标函数的确定
分数阶微分算子 Sα(α ∈[0.1 ~ 0.9]的实际频域响应H(s)与其有理逼近函数的频域响应之间的误差包括幅值误差(dB)和相位误差(deg).因此,本文将粒子群优化算法的目标函数定义为幅值误差绝对值和相位误差绝对值之和:

H(ωi)为分数阶算子的频率响应,H^(ωi)为有理逼近函数的频率响应,ωb<ωi<ωh.L为采样个数,令 L=logspace(ωb,ωh,500).当寻优过程中,逼近函数H^(ωi)稳定时,目标函数取幅值误差绝对值和相位误差绝对值之和.当H^(ωi)不稳定时,目标函数值赋予一个较大值F.
4 仿真实例
用上述介绍的粒子群优化算法对分数阶微分算子Sα(α=0.5)的有理逼近函数H(S)的各系数进行寻优,寻优结果为:
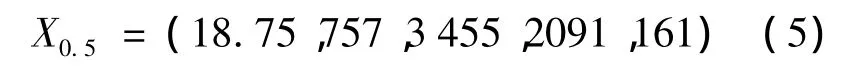
此时目标函数值f=0.789.
由式(5)可得S0.5的有理逼近函数(s)

绘制出(1)和(6)的Bode图,如图1所示(图中叠加了S0.5的理论值):

图1 Oustaloup算法和PSO算法比较
从图1可以得出本文所提的PSO算法逼近精度高于Oustaloup算法,尤其在选取特定频段的端点处拟合效果明显优于Oustaloup算法.
下面分别采用Oustaloup算法和PSO算法对一个分数阶传递函数进行有理逼近,并对两种仿真进行对比.设要逼近的传递函数为:
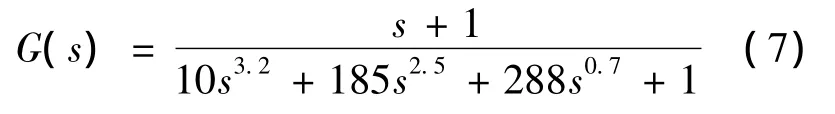
将式(7)改写为:

采用本文所提方法对分数阶微分算子S0.2、S0.7进行有理传递函数系数寻优,得到:
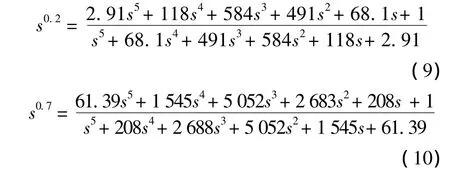
图2给出了传递函数G(S)理论Bode图和Oustaloup算法、本文所提方法得到的有理逼近函数的Bode图,从图中可以看出本文所提方法得到的有理传递函数拟合精度优于Oustaloup算法.

图2 整个系统的Bode比较
从图2可以发现,在中频段两种方法均能取得较好的逼近精度,而在低频段与高频段采用PSO算法的逼近精度明显高于Oustaloup算法.
下面用Oustaloup算法对分数阶微分算子Sα(α=(0.1 ~ 0.9),得到有理逼近传递函数H(s),再运用本文所提方法对分数阶微分算子Sα(α=(0.1 ~ 0.9)的有理逼近函数H(S)的各系数进行寻优,最后分别计算出采用Oustaloup方法和本文方法的幅值绝对误差平均值和相位绝对误差平均值,对比结果如表1所示.
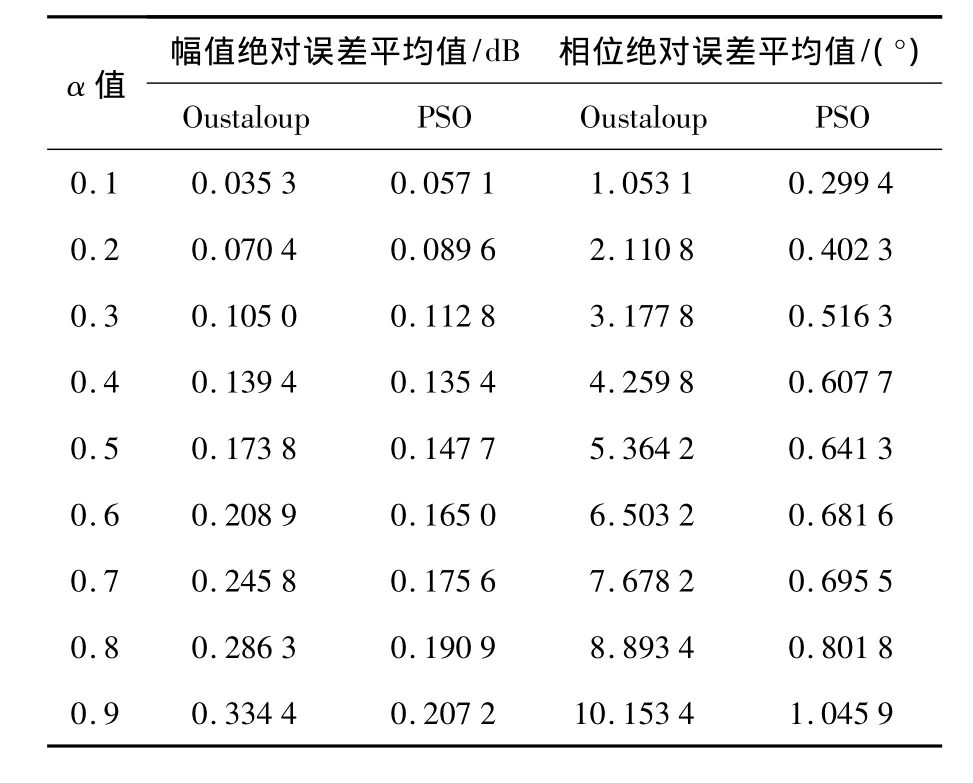
表1 Oustaloup算法与PSO算法误差对比
从表1可以看出,对于 α ∈[0.1 ~ 0.9],PSO算法的相位误差均值明显小于Oustaloup算法.当阶次α>0.3时,PSO算法的幅值误差均值也比Oustaloup算法的幅值误差均值小.当阶次α∈[0.1~0.3]时,PSO算法的幅值误差均值比Oustaloup方法的幅值误差均值要大一点,不过在α<0.3时,这两种方法的幅值误差均值都已足够小,因此不影响PSO算法的优越性.
5 结论
本文提出的一种智能优化算法对提高分数阶算子逼近精度的研究,该方法能够有效的提高拟合精度,此方法所采用的有理传递函数结构由Oustaloup算法得到,有理逼近传递函数的分子、分母通过粒子群优化算法再次寻优得到.通过本文所提方法对分数阶微分算子S0.5进行有理逼近,仿真结果表明所提方法能够取得比Oustaloup算法更高的逼近效果.此外,还利用本文所提方法对一个分数阶传递函数进行有理逼近,结果同样证明了所提方法的有效性.
[1]高朝邦,周激流.基于四元数分数阶方向微分的图像增强[J].自动化学报,2011,37(2):150-159.
[2]HARTLEY T T,LORENZO C F.Dynamics and control of initialized fractional order systems[J].Nonlinear Dynamics,2002,29(1/2/3/4):201-233.
[3]MALTI R,VIETOR S,OUSTALOUP A,et al.An optimal instrumental variable method for continuous-time fractional model identification[C].Proceeding of the 17thWorld Congress on The international Federation of Auto-mation Control Korea,2008:14379-14348.
[4]OUSTALOUP A,LEVRON F,NANOT F,et al.Frequency-band complex noninteger differentiator:characterization and synthesis[J].IEEE Transactions on Circuits Systems I:Fundamental Theory and Applications,2000,47(1):25-39.
[5]BIRGE B,PSOT.A Particle Swarm Optimization Toolbox for matlab[J].IEEE Swarm Intelligence Symposium Proceedings,2003,26(3):24-26.
