基于能耗2L-CVRP模型的绿色物流优化研究

张岐山，刘　虹，张　琳

（福州大学经济与管理学院，福建福州350108）

基于能耗2L-CVRP模型的绿色物流优化研究

张岐山，刘虹，张琳

（福州大学经济与管理学院，福建福州350108）

［摘要］随着我国经济的快速发展，能源消耗日趋严重，其中物流业的能源消耗占能源总消耗的近一半。本文研究了考虑能耗的绿色物流优化，建立了基于能耗2L-CVRP的绿色物流优化模型并给出求解算法。研究结论对提高物流配送的效率，降低能源消耗和绿色物流的建设具有借鉴意义。

［关键词］能源消耗；绿色物流；2L-CVRP；启发式算法

［中图分类号］N945；TP18

［文献标识码］A

［文章编号］1671－511X（2015）04－0100－07

［收稿日期］2015-03-10

［作者简介］张岐山（1962—），男，福州大学经济与管理学院教授，博士生导师，研究方向：物流与供应链、智能算法。

［基金项目］国家社科基金重大招标项目（12&ZD207）；国家自然科学基金项目（71172044，71273047）；高等学校博士点基金项目（20120092110039）；江苏省高校哲学社会科学研究重大项目（2014ZDAXM002）；东南大学基本科研业务费资助项目（2242015S32003）；福建省软科学项目（2013R0057）成果之一。

一、引　言

国家“十二五”节能减排方案要求降低能源消耗强度、减少主要污染物排放总量和合理控制能源消费总量；在加强节能减排管理方面提出了推进交通运输节能减排、开展低碳交通运输专项行动。近年来我国社会物流总额增长快速，而物流领域能源消耗占能源总消耗量的35%- 40%，能耗成本占物流企业总成本的40%-80%［1］。如此高的能耗和成本占比，已成为制约我国节能减排和物流企业发展的关键。因此，如何在发展物流的同时，降低能耗、提高物流效率和降低物流成本，成为一个现实的研究问题。

物流是能源消耗大户，运输过程中的燃油消耗和尾气排放，不仅产生高能耗，而且造成了环境污染。随着全球能源价格的不断上升以及生存环境的持续恶化，人们越来越关注环境的改善以及生命的健康，继而发展出了绿色物流（Environmental Logistics）。绿色物流表达的是在物流活动当中，不仅要降低其对环境的污染，也需要对物流环境进行改善，达到资源充分利用的目的。

绿色物流研究主要集中在逆向物流、废弃物管理、温室气体排放等方面。Bektas等［2］考虑了油耗、温室气体排放量等目标，针对车辆温室气体排放提出了治理污染路径问题；Jabali等［3］考虑相似的影响因素，提出温室气体排放量是速度的非线性函数；肖依永等［4］参考了日本的土地、基础设施与交通旅游省报告［5］，得出车辆净重与燃油消耗的关系、车辆负载与燃油消耗的关系；李进等［6］建立了最小化总油耗的带时间窗车辆路径模型和非满载运输方式下具有固定车辆数的多车型低碳路径优化模型［7］。

在提高物流效率和降低物流成本研究方面，目前的研究主要集中在物流配送集成、车辆路径优化［8-9］等。目前，已有学者进行车厢或集装箱的高效装载研究，以期提高物流运输的装箱容积率和最佳的装卸货效率。现实装箱中大量存在着车厢中的货物无法相互叠放的情况，货物能否装车就取决于货物底面能否拼装入车厢底面中，即二维装箱问题（Two- Dimensional Container Loading Problem，2D-CLP）。在车辆路径问题中考虑2D-CLP，即成为带二维装箱约束的车辆路径问题（VRP with two- dimensional loading con⁃straints，2L-CVRP）［10］，相关研究的成果较少。在模型构建上主要集中在二维装箱约束的单、多车队车辆路径问题的数学模型［11-12］。求解算法主要有精确算法［11］、启发式算法和智能算法［8-10，12-15］。

如何在物流调度管理中，实现对运输线路进行合理设置、提高车辆装载率的基础上，同时考虑节能减排和降低能耗，具有重要的理论意义和实践价值［16］。因此，本文应用2L-CVRP模型，研究降低能耗的绿色物流优化问题。

二、物流的能耗分析

物流是综合性的活动，能耗可发生在较多物流活动中。物流中的能耗主要集中在两个方面：

1.运输车辆能耗。运输活动中车辆的使用占据了物流活动能源消耗的绝大部分，主要为汽油和柴油。与此同时，车辆油耗与车辆数、车辆行驶速度、车载重以及道路状况相关联。车辆能耗对物流过程中的能源消耗产生直接的影响。

2.配送系统能耗。物流配送系统的优化与否也是影响能耗的重要因素，主要包括配送系统环节的各个方面，包括配送效率、车辆路径、储存和装卸搬运等。物流网络系统中的物流路线设置不合理、配送效率不高和车辆装载率低产生了大量能源消耗。

物流运营中，主要消耗的能源是汽油、柴油、电力。而目前全国汽油消耗总量中约90%和柴油消耗量中约60%被各种道路机动交通工具所消耗。因此，本文在绿色物流优化的研究中，考虑车辆燃油消耗，同时结合实际情况，考虑车辆能耗受车速、车载重、道路情况影响，给出车辆单位燃油行驶距离。

车辆从客户i到客户j的车辆单位燃油行驶距离Fij表达式为：

Fij=(α0+α1ν)πijγij。

其中，γij为坡度系数，本文假设道路是平坦的，故γij=1。πij为负载系数，表达式为：

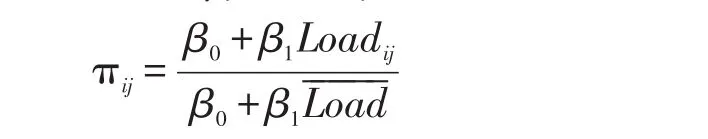
其中Loadij为车辆从客户i到客户j的载重量为车辆长期运营下的平均载重量。α0、α1、β0、β1为正常数。

三、基于能耗的2L-CVRP模型

对物品的配送来说，装箱、运输、能耗是密不可分、相互关联的过程，合理优化装箱问题（Container Loading Problem，CLP），才能更好地对问题进行全局优化，以达到更大程度地优化资源配置、降低运输成本和降低环境影响的目的。本文拟研究单配送中心、单车型、非满载、纯送货、无时间限制、封闭式的VRP，考虑能耗以及二维、规则、离线的2D-CLP。

1.问题描述

2L-CVRP的具体描述如下：

（1）设无向图G={V，E} V，E，其中：

V={ν0，ν1，ν2，…，νn}表示一个配送中心和n个客户的集合；

E={(νi，νj) |(νi，νj∈V )，0i，jn，i≠j}表示路径的集合；矩阵D={dij}为νi到νj的距离；

（2）ν0为配送中心，位置已知，坐标为（x0，y0），配送中心有a辆车，车型相同，车底面积为一个矩形，其长、宽分别为L、W，最大载重量为Q；

（3）配送中心要配送的物品（矩形）有B种类型，编号即1到B，第b（1bB）类物品的长、宽分别为lb、wb，每种物品的重量为qb；

（4）ν0，ν1，ν2，…，νn为n个待服务的客户点，所有的客户点位置已知，其坐标为（xi，yj），客户的需求量是已知的，其中第i（1in）个客户需要mi个物品，物品的类型分别是：Ii1，Ii2，…，Iimi。

车辆路径问题的约束条件：

（1）使用的车辆数目不能大于配送中心的最大车辆数a；（2）车辆从配送中心出发，在服务客户后要返回配送中心；（3）每个客户的需求都得到满足；（4）每个客户仅被访问一次；（5）每辆车所装载的物品的总重量不能超过车的最大载重量Q。

对于每辆车，物品在车厢底面上的摆放需要满足一定的约束条件。如图1所示，建立直角坐标系，坐标系的x、y轴分别平行于车厢的宽、长，原点在车厢的最深处。车厢内的物品，必须满足的装箱问题约束条件：

（1）物品摆放约束。物品须正交地放入车厢中，即物品的底面积的两边都要与坐标轴平行；（2）物品的旋转约束。底面可以进行90度的任意旋转，即如图2所示的两种摆放方式；（3）后进先出（Last In First Out，LIFO）规则。先访问的客户，其物品在装载时要后放入。设车辆目前访问的客户为i，客户j为这辆车在客户i之后访问的任一客户，在对客户i进行服务时，其物品不能被客户j的物品所遮挡，并且可以全部卸载。

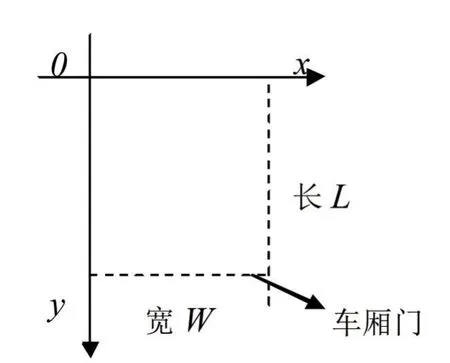
图1　车厢底面直角坐标系

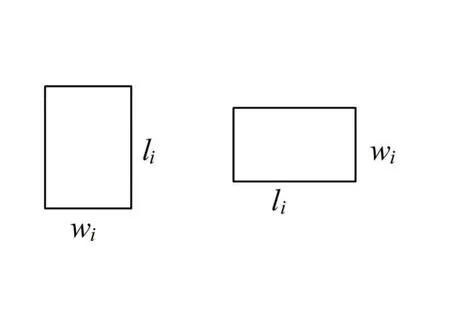
图2　货物摆放的两种方式

2.数学模型

参数符号说明：

K：使用的车辆数；Nk：第辆车服务的客户数；Fij：单位燃油行驶距离；Xkh：第k（1kK）辆车服务的第h（1hNi）个客户；

对于I（i，j）：

则建立以能耗最小为目标的2L-CVRP的数学模型如下：

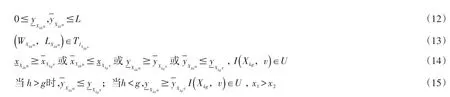
其中：

同一辆车内的其他物品集合

其中，目标函数式（1）为车辆的燃油消耗量最少。式（2）至式（8）表示对车辆路径的基本约束条件：式（2）表示使用的车辆数不能超过配送中心的最大车辆数；式（3）表示每辆车只能访问客户一次；式（4）表示的是不同的车辆不会访问相同的客户；式（5）表示每辆车至少要访问一个客户；式（6）表示所有客户都要被访问；式（7）表示每辆车所装载的物品总重量不能超过车的载重量；式（8）表示每辆车所装载的物品底面积之和不能超过车的底面积。式（9）至式（16）为物品在车厢内的摆放约束：式（9）至式（12）表示物品必须放在车厢内，且不能超过车厢底面范围；式（13）式是对物品的旋转约束限制；式（14）式表示同一车辆内，物品的物理空间不能重合；式（15）式表示后卸载的物品不能阻挡先卸载的物品。

四、求解算法

二维装箱和车辆路径的混合问题，由于这两类问题都属于NP难题，将二者结合考虑也是一类NP难题。针对考虑能耗的2L-CVRP数学模型，本文设计了微粒群算法（Particle Swarm Optimization，PSO）与局部搜索算法（Local Search，LS）相结合的算法来进行求解。整个算法主要分为两个层次：主框架使用的是微粒群算法来安排每辆车的行驶路径，其中嵌套了一层局部搜索算法来求解装箱方案，嵌套框架对装箱方案进行判断，将其求解结果返回到主框架，主框架部分会根据返回值来对路径方案进行调整，以此来优化车辆行驶路径。

1.基于能耗的CVRP的微粒群求解算法

针对基于能耗的2L-CVRP优化模型，给出PSO求解算法。

Step 1：对粒子进行编码。每个粒子由两部分编码构成，第一部分是车辆的使用情况（particle1），第二部分是车辆服务客户的序列（particle2）。其中，particle1是一维数组，维度为车辆数，每个元素随机取0或1（0表示未选用车辆，1表示选用车辆），相应的速度编码随机取［-1，1］之间的实数；particle2是二维数组，维度为Vehi*Cust（Vehi为车辆数，Cust为客户数），每个元素随机取［0，Cust］之间的整数（0表示未服务该客户），相应的速度编码随机取［-Cust，Cust］之间的实数，由于particle2是随机产生的，客户编码有可能出现重复，在适应度函数判断时转换成相应的客务序列。

Step 2：设定算法参数，包括种群大小num_particle，最大迭代次数itmax，惯性权重w1，加速系数c1、c2。

Step 3：随机初始化种群中各粒子的位置particle和速度V。

Step 4：燃油消耗f为目标函数，以其值最小为目标进行进化。若粒子不满足约束条件，对粒子加以惩罚，令其适应度fitness=fitness+M，M是一个很大的数。

Step 5：初始化种群，令各粒子个体最佳位置pbest为当前位置，对应的适应度为个体最优值pbest_val⁃

ue，比较pbest_value，最小值为群体最优值gbest_value，pbest中的最佳位置为群体最佳位置gbest。

Step 6：按微粒群算法的速度和位置更新公式更新各微粒的速度和位置。

Step 7：重复Step4，比较各粒子当前位置的适应度与个体历史最优值pbest_value，令较小者的位置为pbest的位置，令其值为当前个体最优值pbest_value。

Step 8：比较当前个体最优值pbest_value与群体历史最优值gbest_value，令较小者的位置为gbest的位置，令其值为当前群体最优值gbest_value。

Step 9：若终止条件满足（达到最大迭代次数）则退出，并输出群体最优位置gbest及其值gbest_value，否则继续Step6。

2.求解2D-CLP的局部搜索算法

由于车辆装载的物品需要满足先进后出、物理空间不能重合、摆放不能超出车厢、总重量不能超过车辆载重等众多约束条件，为了符合不同的实际应用背景，选择的装箱算法必须具备灵活的特点。同时，选用的装箱算法能被主框架中的微粒群算法反复调用，其搜索装箱结果的性能要求高效，才能提高整个算法的效率。本文采用局部搜索算法LS来求解二维装箱问题。

LS算法的输入参数为客户序列no_V2C，进行约束判断之后，返回装箱是否成功以及装箱方案，若装箱成功返回1（即true），若装箱失败则返回0（false）。为了填充装箱，在局部搜索算法中，引入启发式算法--最底最左位置填充算法（Bottom-Left-Fill，BLF）。该算法输入的是LS算法的一个解，即每辆车装载的物品序列no_itemV，判断该装箱方案是否满足各个装箱约束，当物品无法装箱或者全部物品都装箱完成算法结束，最后输出的是成功装箱的物品个数以及物品的摆放坐标。

Step 1：设定算法的迭代次数lsmax。

Step 2：生成初始解no_itemV0，令其为当前解no_itemV。将解表示为一维元胞数组，维度为车辆数。其中，每个元胞表示一辆车的物品序列，其为二维数组，维度为num_itemV*2，第一列表示的是客户编码，第二列表示的是客户对应的物品编号。

Step 3：迭代lsmax次

Step 3.1：调用BLF算法对初始解进行装箱判断，返回值为num_count和sel_pos；

Step 3.2：若num_count=num_itemV，则表示装箱成功，返回true和装箱方案，并跳出循环；否则，在［1，num_count+1］中随机产生整数p，在［1，num_itemV+1］中随机产生整数q，将no_itemV中的第q、p个物品的位置进行交换。

Step 3.3：重复Step 3.1和Step 3.2，直到运行到lsmax次结束，返回false。

五、数值算例

本文以文献［11］中的测试算例作为模拟样本①测试算例来自于网站：http：//prolog.univie.ac.at/research/VRPandBPP/.，并在此基础上，增加计算单位燃油消耗行驶距离的相关参数，如表1所示，表中的参数主要从交通和能源部门［17-21］的实际数据统计得到。其中，Load是在车辆载重为45000磅的情况下的平均载重，即平均载重为车辆载重的74.342222%左右，根据不同算例中车辆的载重不同，该值会进行相应的调整。

选取的算例是0302，客户数为20，车辆数为5，物品数为29，车辆的载重为85，长为40，宽为20，配送中心（用0表示）和客户的坐标、客户需求、客户所需的物品数以及每个物品的长宽如表2所示。

PSO算法的参数设置如下：种群规模num_particle为100，认知部分和社会部分加速系数c1=c2=2.05，粒子的惯性权重w1=0.729，最大迭代次数itmax为200。LS算法的参数设置如下：最大迭代次数lsmax为100。

该模型的仿真结果中，最优解的燃油消耗值为14.819021，仿真实验得到的计算结果见表3-表5，粒子迭代过程的最优轨迹见图3。

实验结果表明，在物流中考量能源消耗所构建的优化模型和求解方法是可行的，可以引导绿色物流车辆路径的合理设计。

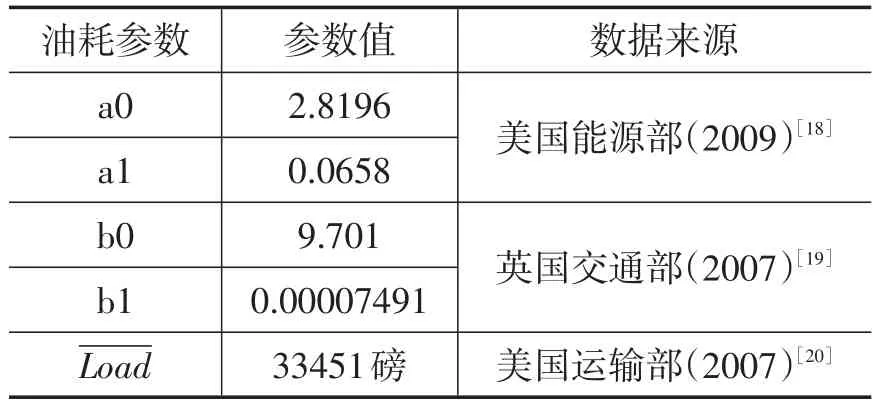
表1　单位燃油消耗的行驶距离F的相关参数

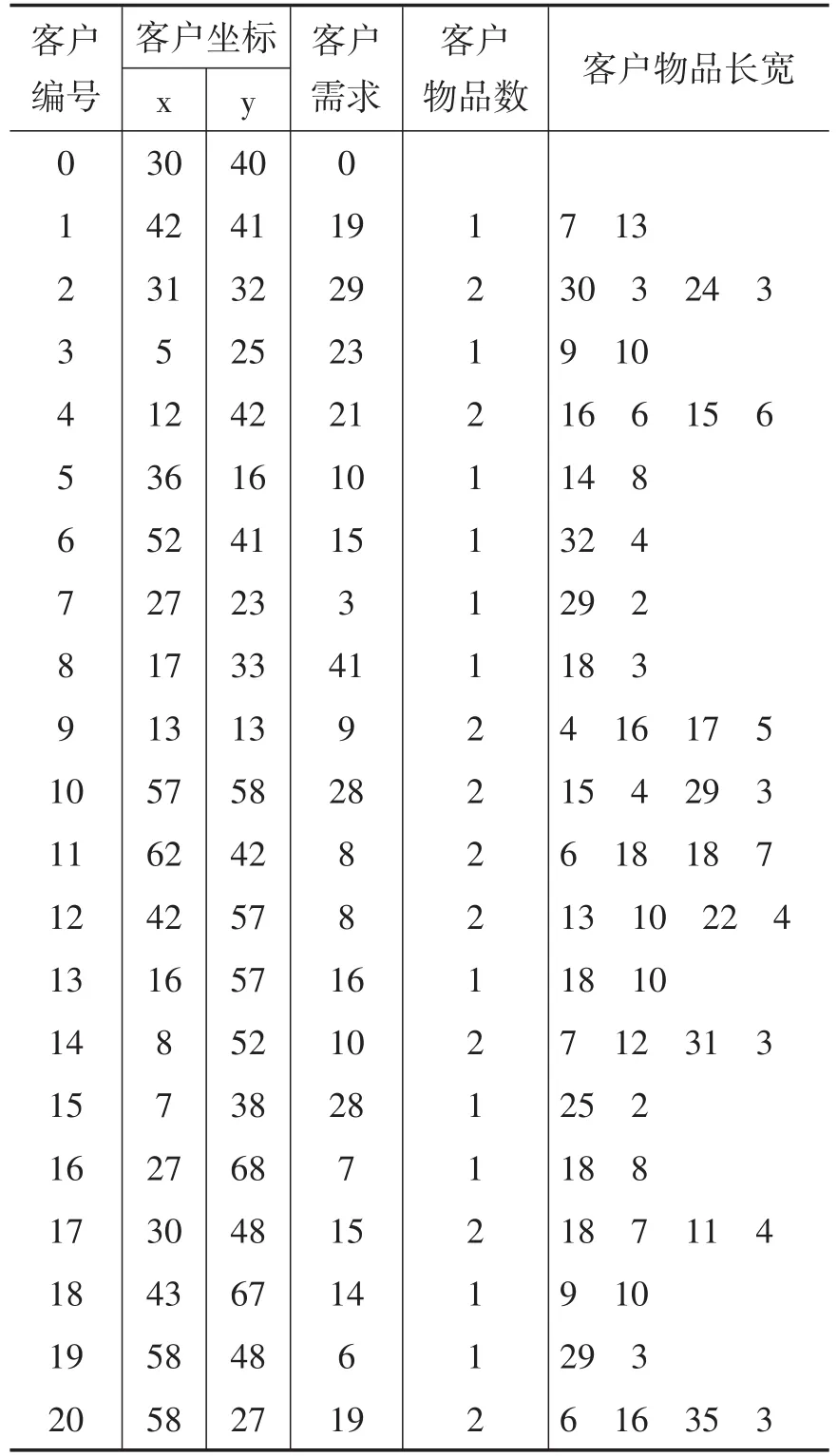
表2　算例的数据

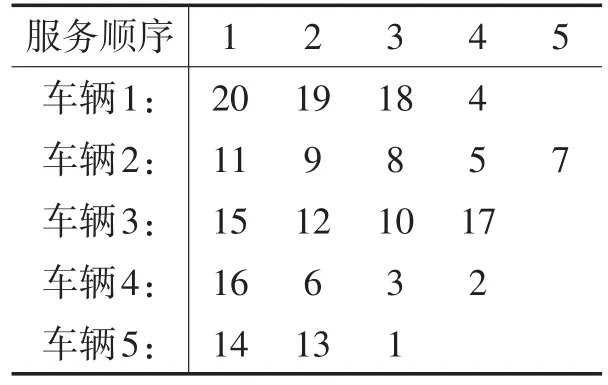
表3　最优客户序列

表4　最优物品摆放序列

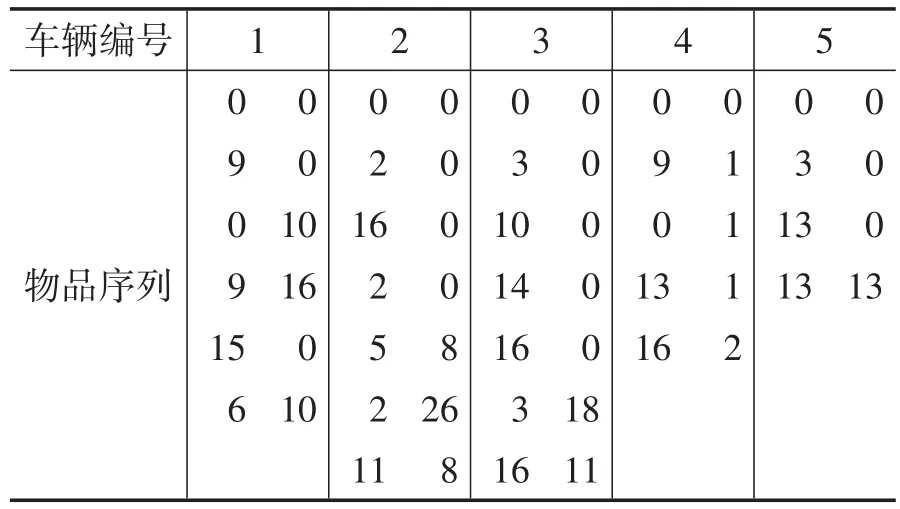
表5　最优物品坐标

图3　粒子迭代过程的最优轨迹图

六、结　语

我国能源消费总量正随着经济的快速发展而持续增长，物流业是能源高消耗的产业，其中运输过程占整个物流系统中的能耗比重最大。在降低能耗的研究中，考虑绿色优化物流，不仅可以提高物流配送的效率，而且可以降低能源消耗，对绿色物流的建设具有低碳环保的实际意义。通过研究，可以得出以下结论：

（1）建立和倡导绿色物流，可以降低物流运输业的能源消耗，从而缓解我国的能耗压力。

（2）降低车辆燃油消耗和提高装箱效率，建设低碳环保的绿色优化是可行的。说明应加大降低能耗和绿色物流优化研究，不仅可以提高物流配送的效率，而且可以降低能源消耗，对绿色物流的建设具有实际意义。

（3）物流系统中的节能减排是一个复杂的系统工程，可以依靠技术进步来逐步解决。政府应大力推

广新型、高效的物流技术，积极推行物流标准化建设，促进各种物流装卸设施等物流技术和设备的标准化，以帮助物流行业有效地建立、实施和拓展绿色物流的科学管理，促进我国物流系统与国际系统的接轨。

［参考文献］

［1］刘潇潇，李志君．关于物流运营中能耗问题的研究［J］．时代经贸，2009（5）：90-91．

［2］Bektas,T，Laporte G. The Pollution-Routing Problem［J］．Transportation Research Part B：Methodological. 2011，45（8）：1232-1250．

［3］Jabali O，Van Woensel T，de Kok A G. Analysis of Travel Times and CO2Emissions in Time-Dependent Vehicle Routing［J］．Production and Operations Management. 2012，21（6）：1060-1074．

［4］Xiao Y，Zhao Q，Kaku I，et al. Development of a fuel consumption optimization model for the capacitated vehicle routing problem. Computers & Operations Research，2012，39（7）：1419-1431.

［5］Website Japanese Government. http：//www.mlit.go.jp /common/000037099. pdf［Z］．18 March 2010．

［6］李进，傅培华．基于能耗的带时间窗车辆路径问题建模与仿真［J］．系统仿真学报．2013，（6）：1147-1154．

［7］李进，傅培华．具有固定车辆数的多车型低碳路径问题及算法［J］．计算机集成制造系统．2013，19（6）：1351-1368．

［8］Gendreau M，Iori M，Laporte G，et al. A Tabu Search Heuristic for the Vehicle Routing Problem with Two-Dimensional Loading Constraints ［J］．NETWORKS. 2008，51（1）：4-18．

［9］Zachariadis E E，Tarantilis C D，Kiranoudis C T. A Guided Tabu Search for the Vehicle Routing Problem with two-dimensional loading con⁃straints［J］．European Journal of Operational Research. 2009，195（3）：729-743．

［10］王征，胡祥培，王旭坪．带二维装箱约束的物流配送车辆路径问题［J］．系统工程理论与实践．2011，31（12）：2328-2341．

［11］Iori M，Salazar-Gonzlez J，Vigo D. An exact approach for the vehicle routing problem with two-dimensional loading constraints［J］．Trans⁃portation Science，2007，41（2）：253-264.

［12］Leung S C H，Zhang Z，Zhang D，et al. A meta-heuristic algorithm for heterogeneous fleet vehicle routing problems with two-dimensional loading constraints［J］．European Journal of Operational Research. 2013，225（2）：199-210．

［13］Leung S C H，Zhou X，Zhang D，et al. Extended guided tabu search and a new packing algorithm for the two-dimensional loading vehicle routing problem［J］．Computers & Operations Research. 2011，38（1）：205-215．

［14］Fuellerer G，Doerner K F，Hartl R F，et al. Ant colony optimization for the two-dimensional loading vehicle routing problem［J］．Comput⁃ers & Operations Research. 2009，36（3）：655-673．

［15］Leung S C H，Zheng J，Zhang D，et al. Simulated annealing for the vehicle routing problem with two-dimensional loading constraints［J］．Flexible Services and Manufacturing Journal. 2010，22（1-2）：61-82．

［16］靳方平．基于低碳经济视角的车辆路径优化理论与方法研究［D］．中南大学，2013．

［17］叶君好．绿色随机多目标车辆路径问题研究［D］．南开大学，2013．

［18］US Department of Energy. Office of Energy Efficiency and Renewable Energy［R］．Transportation Energy Data Book，28th ed. Washington D.C.，USA：USDoE，2009．

［19］UK Department for Transport．Effects of Payload on the Fuel Consumption of Trucks，2007．

［20］US Department of Transportation，Federal Highway Administration. Office of Freight Management and Operations［R］．Development of Truck Payload Equivalent Factor. Washington D. C.，USA：USDoE，2007．

［21］Suzuki Y. A new truck-routing approach for reducing fuel consumption and pollutants emission［J］．Transportation Research Part D：Transport and Environment.2011，16（1）：73-77．