三相Vienna整流器单闭环及中点电位平衡控制策略*
2015-02-18马辉谢运祥
马辉 谢运祥
(华南理工大学 电力学院, 广东 广州 510640)
三相Vienna整流器单闭环及中点电位平衡控制策略*
马辉谢运祥
(华南理工大学 电力学院, 广东 广州 510640)
摘要:为降低Vienna整流器的生产成本,提高控制算法的工作效率,设计了基于无电流传感器的单闭环控制策略.针对Vienna整流器的中点电位波动和传统三电平空间矢量调制(SVPWM)计算繁琐的问题,引入一种基于载波调制的简化等效SVPWM技术,主要是通过在零序分量中加入平衡因子来控制中点电位平衡.单闭环控制算法和等效SVPWM相结合大大简化了控制系统的设计过程,提高了整个控制系统的工作效率.最后通过实验验证了该控制算法的正确性和高效性.
关键词:Vienna整流器;单闭环控制策略;中点电位平衡;空间矢量调制;载波调制;零序分量;脉宽调制
传统无电流传感器控制策略是一种间接电流控制算法,采用电流重构技术来获得网侧三相电流信息,以实现无电流传感器控制策略[1-5].该算法虽节约成本,但是需要重构网侧电流,从而会降低电流内环的控制精确性;其与传统电压电流双闭环控制策略类似,采用双闭环控制,电流波形受电流内环控制参数影响较大,并且控制算法较复杂.文中简化传统双闭环控制算法,降低生产成本,提出无电流传感器的单闭环控制算法;由于该算法是基于相角控制原理,无需重构网侧电流信息,即无需电流内环,从而化简传统双闭环控制策略;因此无需电流传感器从而降低生产成本,该策略具有双重研究意义.
Vienna整流器与传统三电平整流器的性能类似,用以解决传统三电平整流器中点电位平衡问题的控制算法,可以应用在Vienna整流器中[6-9].关于中点电位平衡控制算法的研究主要有两方面,一是从平衡因子上做算法研究,文献[10-11]中提出模糊控制算法,该算法虽不易受控制系统影响,便于移植,但设计控制规则较为繁琐,不易实现编程,在整流器研究中应用较少,而目前主要采用PI控制器.另一方面是研究调制方式,文献[12]中采用传统三电平空间矢量调制(SVPWM),通过PI控制器来分配冗余矢量对的作用时间,实现中点电位平衡;其需要分配大扇区,然后分配小扇区,运用三角函数计算矢量的作用时间,运算过程较繁琐,过多占用控制芯片资源.为此,文献[13]中采用三电平转二电平的简化SVPWM,虽简化了扇区分配过程,但时间计算上与前者类似;为简化时间计算过程,文献[13]中提出基于60°坐标系的SVPWM,该算法避免运用三角函数来计算时间,虽简化计算过程,但引入转换矩阵增加分配扇区的工作量;文献[14]中利用多电平调制技术,针对三相三线制三电平拓扑结构,提出基于载波调制的等效空间调制策略,因其兼备SVPWM与SPWM的双重优点,该调制算法在三线制整流器中受到国内外学者的广泛关注.
关于零序分量,Vienna整流器与传统三电平整流器不同,需要重新分析计算Vienna整流器的零序分量.文献[11]中针对Vienna整流器做了SVPWM与SPWM等效分析,采用间接方式分析零序分量与冗余小矢量之间的关系,其结论中的等效关系式冗余,容易造成零序分量分配错误,导致输入电流畸变以及中点电位不平衡.文中简化SVPWM与SPWM的等效分析过程,除去文献[11]结论中的冗余式,提出在零序分量中加入平衡因子精确控制中点电位平衡的等效SVPWM,对平衡因子的控制采用PI控制器,详细推导基于无电流传感器的单闭环控制策略,给出控制方案的具体设计过程,化简加入平衡因子后零序分量的推导过程,最后利用实验样机来验证控制策略的有效性.
1Vienna整流器数学模型
三相Vienna整流器主电路拓扑结构如图1所示,ua、ub、uc为三相输入电源电压;ia、ib、ic为三相输入电流;ip、in输出直流母线正向和负向电流;L1、L2、L3为三相滤波电感,其值为L;Cp、Cn为直流侧上下电容,其值为C;vcp、vcn分别为上下直流电容的电压;RL为输出电阻负载;Sa,b,c为三相开关函数,每个双向开关由1个主控开关器件和4个二极管组成,结构如图1左半部所示;每只桥臂上存在上下两只快速恢复二极管(a相:Dap、Dan).

图1 三相Vienna整流器主电路拓扑Fig.1 Topology of three phase Vienna-type rectifier
Vienna整流器是电流驱动型功率因数校正整流器,开关管两端的电压由开关管自身状态和输入电流方向共同决定[15].以a相为例,输入电流为正,开关开通,开关管被钳位在直流正极,此时开关两端电压vAN为vcp(vdc/2);若输入电流为负,开关开通,开关管被钳位在直流负极,此时开关两端电压vAN为vcn(-vdc/2);开关管关断,无论电流正负,开关管被钳位在直流中点N.
电网处于理想平衡状态,Vienna整流器工作在连续电流模式下,该电路可以简化成与调制波函数相关的平均状态数学模型,因此,每个开关周期内的平均状态模型如图2所示.mip(i代表a,b,c)表示输出电压为vdc/2的调制波时间函数,min(i代表a,b,c)为输出电压-vdc/2时的调制波时间函数;输出电压的平均值可表示为mipvcp+minvcn.稳态时,忽略开关频率谐波,根据电路元件的微分性质和基尔霍夫电压定律得到

(1)
其中,

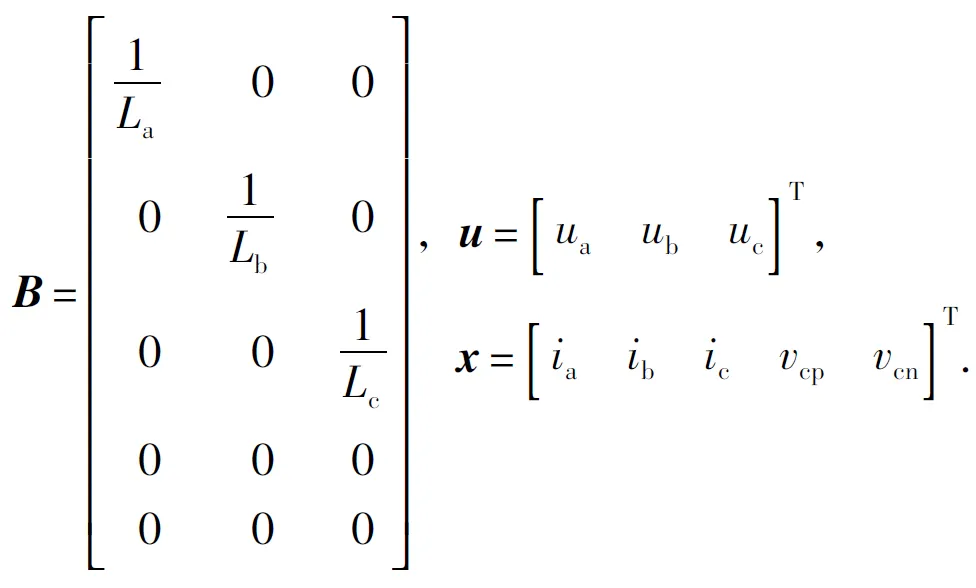
La=Lb=Lc=L,vcp=vcn=vdc/2,将三相坐标系的状态空间方程转化到同步旋转极坐标系下,通过旋转变换可得到
(2)


图2 平均状态空间模型Fig.2 State-space average model
2单闭环控制算法
文中提出基于相角控制原理的单闭环控制策略,其控制原理框图如图3所示.该算法利用直流侧电压与参考给定电压的误差,将误差信号作为PI控制器的输入量,PI控制器的输出作为电源电压与功率开关端电压的相角差,它被用于调制波定向.由于调制波的幅值Mα在一个开关工作周期内变化很小,能量传递的过程主要依靠相角Mθ来进行控制,另外对幅值的合理控制是Vienna整流器工作在单位功率因数下的重要条件,同时也是获得高质量正弦电流波形的关键因素.
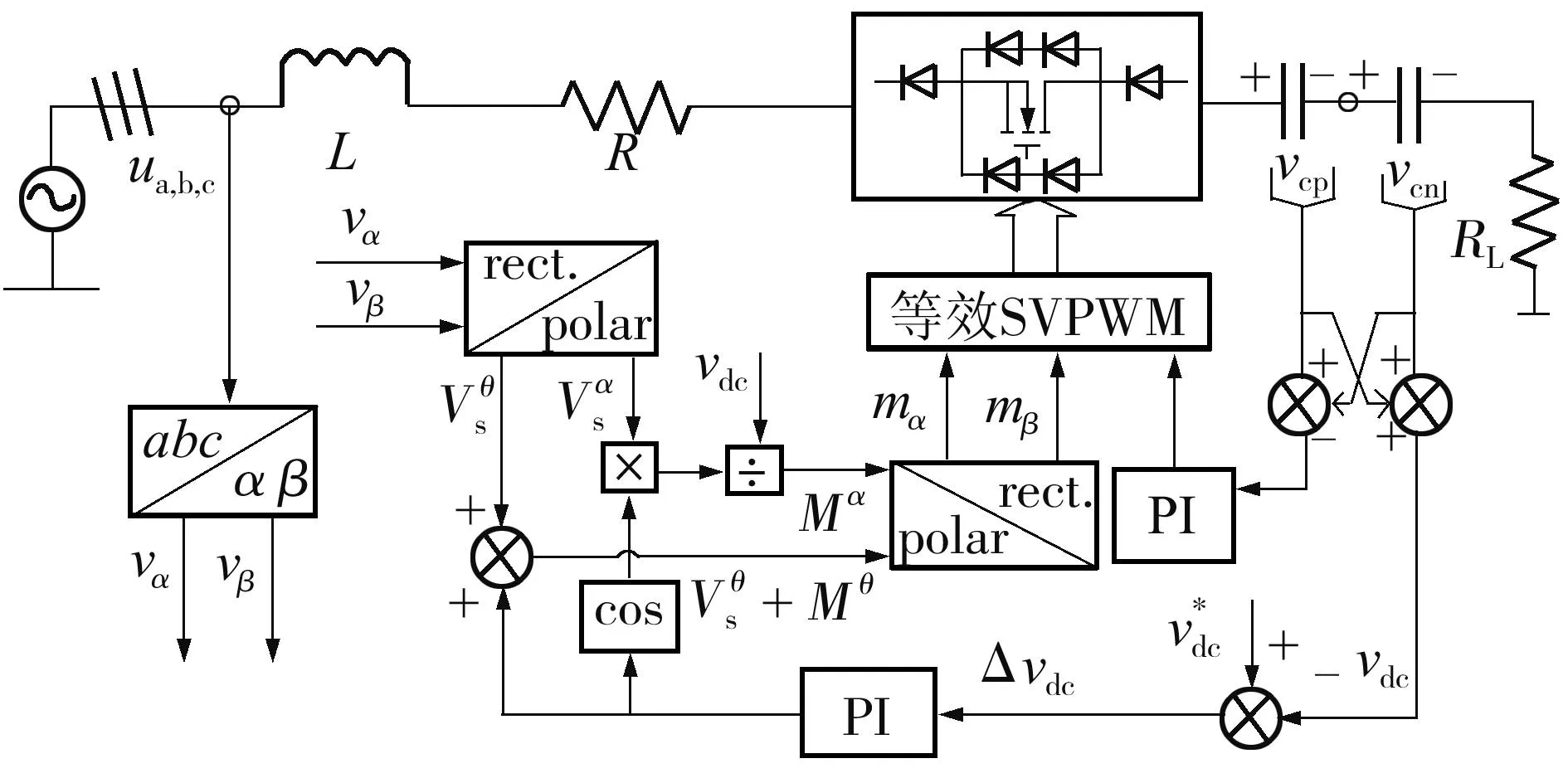
图3 单闭环控制算法原理框图Fig.3 Block diagram of the proposed single closed-loop strategy
电压外环PI调节器是设计的关键,由式(2)可知相角与直流电压的数学平均状态模型,系统的控制量与被控量之间存在着非线性关系,不便于分析和设计控制系统,因此需要将上述动态数学模型用小信号模型进行处理,得到线性化的小信号数学模型:
(3)
式中,


直流侧vdc和mΘ之间的等效传递函数如下:
(4)

整个电压外环传递函数是一个3阶系统,通过合理设计PI调节器使系统获得充裕的相角裕度和增益裕度,按照额定参数计算,在最佳阻尼比下,PI调节器的比例和积分控制参数分别为kp≈14.5,kI≈187.
3基于等效SVPWM的中点电位平衡控制
Vienna整流器的开关工作组合状态少于传统三电平整流器,因此注入的零序分量不同于传统三电整流器.文中化简Vienna整流器零序分量的推导过程,建立三电平SVPWM与SPWM的内在联系;为使中点电位平衡,在零序分量中加入平衡因子,使新合成的零序分量具有良好的平衡能力.下文详细分析具有中点电位平衡能力的等效SVPWM.


图4 6大扇区和第1扇区电压空间矢量Fig.4 Six sectors and space vectors of sector I
如图4所示,以第1大扇区为例,选取位于小扇区A的目标矢量Vref,三相电流的相位Ia位于上半周,而Ib和Ic位于下半周.目标矢量采用最近矢量合成原则,利用伏秒平衡原理,Vref是由长矢量V4、中矢量V2和短矢量V3(V3+,V3-)合成,其时间分别为T4、T2和T3,则上述关系的表达式如下:
V4T4+V3T3+V2T2=VrefTs
(5)
式中,Ts为采样周期,同时各个矢量的作用时间满足以下关系:
T4+T3+T2=Ts
(6)
将式(5)按实部和虚部分别展开:
(7)

(1-f)V3+=fV3-
(8)
式中,f为冗余矢量的分配时间系数,f的范围在0~1之间,它由上下电容的电位差决定,通过PI调节器对电位差进行控制,即使在负载不平衡的情况下,中点电位也能够得到有效的平衡控制.为消除谐波和减小开关管通断损耗,采用7段对称矢量合成模式,每次矢量变化一次,开关管动作一次,从正小冗余矢量或负冗余矢量开始[11,15].
V3+(1,0,0)-V2(1,0,-1)-V4(1,-1,-1)-V3-(0,-1,-1)
-V4(1,-1,-1)-V2(1,0,-1)-V3+(1,0,0)
(9)
利用式(7)-(9)可以得出三相开关管的工作时间:
(10)
当目标矢量位于其他扇区时,依照上述的分析方式可以推出相应的零序分量,总结可得出每一个扇区的零序分量,为使它具有统一的表达形式,重新定义三相调制波:

(11)
式中,k代表a,b,c.则注入的零序分量如下:
d0=f(1-Mmax+Mmin)-Mmin
(12)
式(12)与文献[5]中推出的结论相同,等效SVPWM原理框图如图5所示,零序分量的推导程序在文章后面的附录中;三电平等效SVPWM采用双重载波对三相调制波进行调制,通过输出相应的逻辑电平来控制开关管的工作状态.
为直观分析等效SVPWM后的调制波,比较注入零序分量前与后的调制波的区别,通过比较图6(a)和(b)可知,等效SVPWM可提高电压利用率,简化传统SVPWM的实现过程.设调制比m为0.78,平衡因子r为0.5,零序分量和新合成调制波的仿真结果如图6(b)所示.
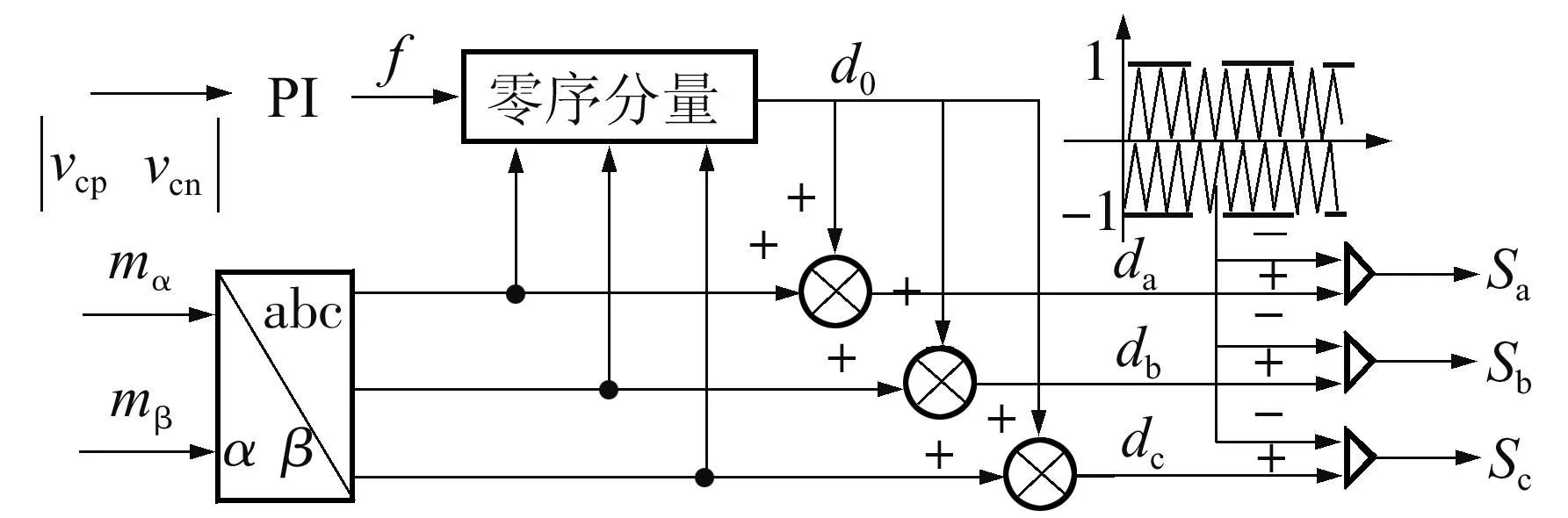
图5 等效SVPWM原理框图Fig.5 BlockdiagramoftheequivalentSVPWMalgorithm
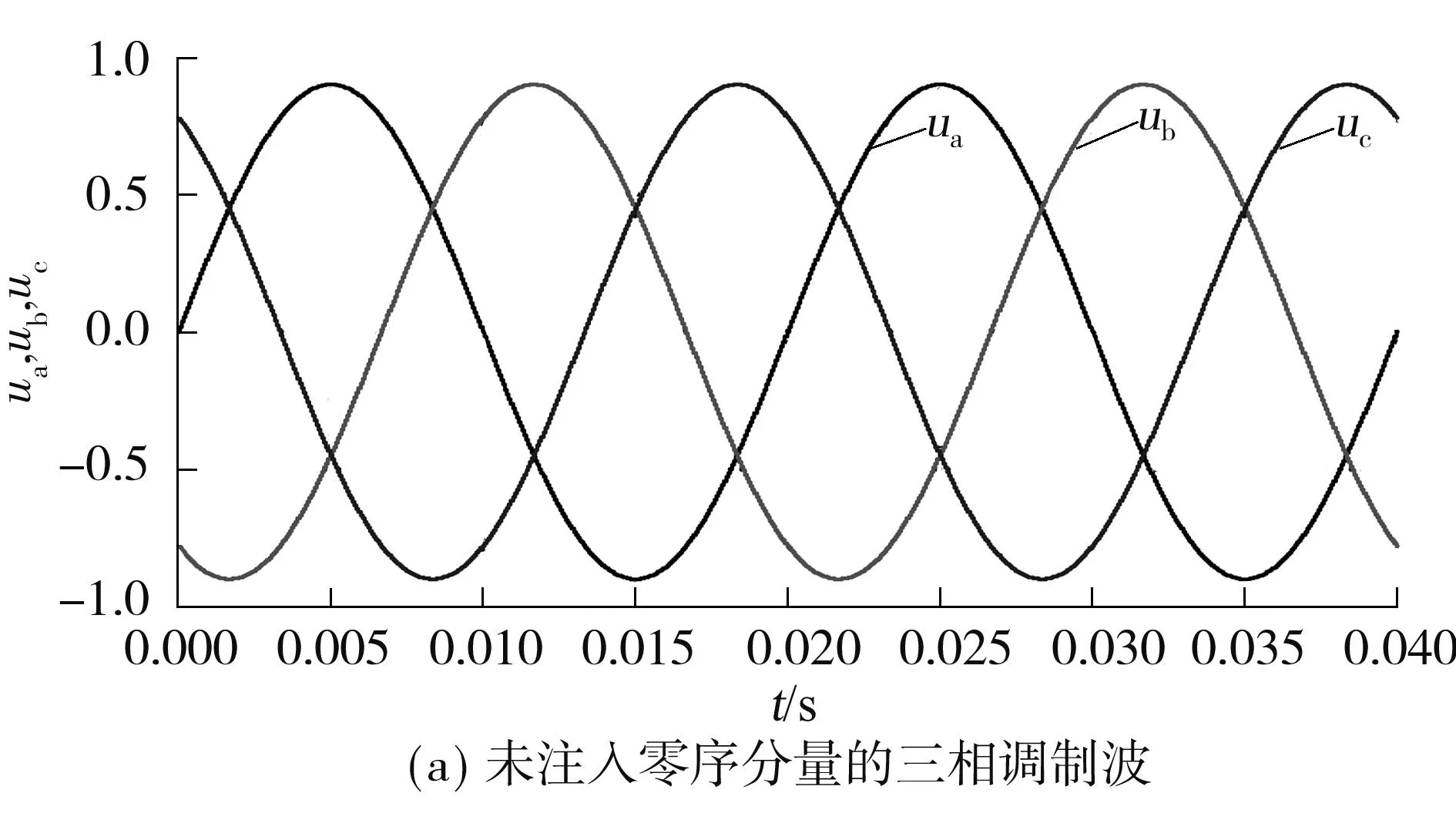

图6 调制波的对比及零序分量波形Fig.6 Comparison of modulated waves and the zero-sequence component wave(r=0.5,m=0.78).
4实验验证
为验证上述控制策略,基于TMS320F2812控制核心芯片,设计输出额定功率为1.98 kW的实验样机.电路设计参数如下:三相电源为110 V/50 Hz;直流给定输出电压为300 V;额定输出功率为1.98 kW;开关频率为15 kHz;三相电感为4 mH;直流侧上下电容为2 200 μF.
负载为45 Ω,图7为Vienna整流器从不控状态到可控状态的电压、电流波形图.从图7(a)中可看出输入电流在一个周期内达到稳定,不控到可控过程中电流畸变不大,对开关器件的电流冲击几乎不存在;图7(b)表明,直流电压能够实现平稳过渡,不存在超调,说明单闭环控制策略能够对直流电压实现无超调稳定控制.
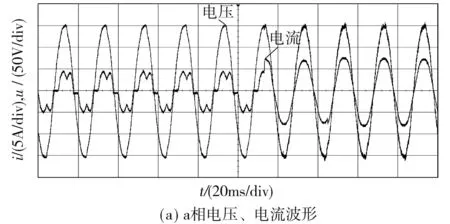
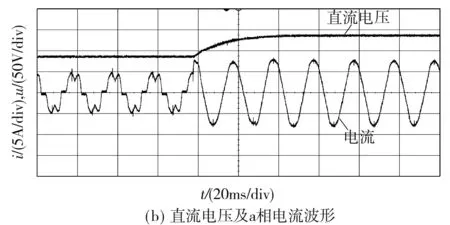
图7 从不控状态到可控状态的电流和电压波形Fig.7 Current and voltage waveforms from startup state to steady state
图8为直流侧上下电容的电压波形,从图8可知,加入平衡因子的零序分量能够很好地控制中点电位平衡.取稳态波形,图9(a)表示a相电流和直流电压波形,图9(a)表明单闭环控制策略具备较好稳定性,从图9(b)可得出,网侧输入电流与电压电位同相位,Vienna 整流器在近似单位功率因数状态稳定运行.

图8 直流侧上下电容电压波形Fig.8 Voltage waveforms of dc-link top-bottom capacitors


图9 稳态实验波形图Fig.9 Experiment waveforms of steady state results
5结论
文中针对三相Vienna整流器,设计了一种无电流传感器的单闭环控制策略,该策略是对传统双闭环控制策略的简化,省去了电流内环,在实际生产中提高了设计控制算法效率,使控制系统具有高效性.由于Vienna整流器的SVPWM与传统三电平整流器的SVPWM不同,在研究三电平整流器等效SVPWM的基础上,文中探索了适用于Vienna整流器的等效SVPWM技术,简化等效过程,程序设计更为高效,并在该零序分量中加入平衡因子,使新型调制方式具有良好的中点电位平衡能力,并兼备SVPWM和SPWM二者的优点.最后,通过样机对所提方案进行验证,实验结果验证了控制算法的有效性.
参考文献:
[1]符强,林辉,贺博,等.无电流传感器的四开关三相无刷直流电机驱动控制新策略 [J].中国电机工程学报,2006,26(17):148-153.
Fu Qiang,Lin Hui,He Bo,et al.A novel control scheme of four-switch three-phase brushless dc motor without current sensor [J].Proceeding of the CSEE,2006,26(17):148-153.
[2]毛鸿,吴兆麟,王毅,等.三相电压型PWM整流器无电流传感器控制策略研究 [J].电工技术学报,2001,4(2):56-60.
Mao Hong,Wu Zhao-lin,Wang Yi,et al.Study on the sensorless current control strategy of three-phase voltage-source PWM rectifier [J].Transaction of Chinese Electro Technical Society,2001,4(2):56-60.
[3]Lim D L D.AC voltage and current sensorless control of three-phase PWM rectifiers [J].IEEE Transactions on Power Electronics,2002,17(6):883-890.
[4]Kennel R M,linke M,Szczupak P.“Sensorless” control of 4-quadrant-rectifiers for voltage source inverters (VSI) [C]∥Power Electronics Specialist Conference. [S.l.]:IEEE,2003:1057-1062.
[5]Chiu H J,Wang C M,Su Y C,et al.A novel three-phase switch-mode rectifier without current sensors [C]∥Power Electronics and Drive Systems.[S.l.]:IEEE,2003:1537-1539.
[6]Kolar J W,Drofenik U.Current handling capability of the neutral point of a three-phase/switch/level boost-type PWM (VIENNA) rectifier [C]∥Power Electronics Specialists Conference.[S.l.]:IEEE,1996:1329-1336.
[7]Viitanen T,Tuusa H.Space vector modulation and control of a unidirectional three-phase/level/switch VIENNA I rectifier with LCL-typeAC filter [C]∥Power Electronics Specialist Conference. [S.l.]:IEEE,2003:1063-1068.
[8]姜海鹏,刘永强.带中点电位平衡控制的VIENNA整流器简化SVPWM双闭环控制 [J].电机与控制学报,2014,18(2):35-41.
Jiang Hai-peng,Liu Yong-qiang.Simplified SVPWM dual closed loop vector control method for vienna rectifier with midpoint potential balance control [J].Electric Machines and Control,2014,18(2):35-41.
[9]陈娟,何英杰,王新宇,等.三电平空间矢量与载波调制策略统一理论的研究 [J].中国电机工程学报,2013,33(9):71-78.
Chen Juan,He Ying-jie,Wang Xin-yu,et al.Research of the unity theory between three-level space vector and carrier-based PWM modulation strategy [J].Proceeding of the CSEE,2013,33(9):71-78.
[10]陈鑫兵,何礼高.基于模糊控制的三电平逆变器中点电位平衡策略 [J].电工技术学报,2007,22(10):103-109.
Chen Xing-bing,He Li-gao.Research on neutral point potential balance of three-level inverter based on fuzzy logic control strategy [J].Transaction of Chinese Electro Technical Society,2007,22(10):103-109.
[11]Ma Hui,Xie Yun-xiang,Sun Biao-guang,et al.Modeling and direct power control method of vienna rectifiers using sliding mode control approach [J].Journal of Power Electronics,2015,15(1):159-171.
[12]Rixin L,Fei W,Burgos R,et al.Average modeling and control design for vienna-type rectifiers considering the dc-link voltage balance [J].IEEE Transactions on Power Electronics,2009,24(11):2509-2522.
[13]王裕,谢运祥.改进的三相四线制有源电力滤波器电流检测 [J].华南理工大学学报:自然科学版,2014,42(12):112-119.
Wang Yu,Xie Yun-xiang.Improved harmonic current detection for three-phase four-wire active power filter [J].Journal of South China University of Technology:Natural Science Edition,2014,42(12):112-119.
[14]周卫平,吴正国,唐劲松,等.SVPWM的等效算法及SVPWM与SPWM的本质联系 [J].中国电机工程学报,2006,26(2):133-137.
Zhou Wei-ping,Wu Zheng-guo,Tang Jin-song,et al.A novel algorithm of SVPWM and the study on the essential relationship between SVPWM and SPWM [J].Proceeding of the CSEE,2006,26(2):133-137.
[15]Burgos R,Lai R,Pei Y,et al.Space vector modulator for vienna-type rectifiers based on the equivalence between two-and three-level converters:a carrier-based implementation [J].IEEE Transactions on Power Electronics,2008,23(4):1888-1898.
[16]Ma Hui,Xie Yun-xiang,Shi Ze-yu,et al.Voltage balance control of vienna-type rectifier using SVPWM based on 600 coordinate system [C]∥Electrical Machines and Systems.HangZhou:ICEMS,2014:1537-1539.
Single Closed-Loop Control and Neutral-Point Potential Balance Control of Three-Phase Vienna-Type Rectifier
MaHuiXieYun-xiang
(School of Electrical Power,South China University of Technology,Guangzhou 510640,Guangdong,China)
Abstract:In order to reduce the cost of three-phase Vienna-type rectifiers and improve the efficiency of corresponding control algorithms,a single closed-loop strategy without current sensor is designed.Aiming at the problems of the neutral point voltage unbalance and the complex calculation of the space vector pulse width modulation(SVPWM)topology of Vienna-type rectifiers,a simplified equivalent SVPWM technology is proposed based on carrier modulation,which controls the neutral-point potential balance mainly by adding the balance factor into the zero-sequence component.The combination of the single closed-loop control algorithm with the equivalent SVPWM simplifies the design process of the control system,and improves the efficiency of the whole control system.Finally,the correctness and effectiveness of the proposed algorithm are verified by an experiment.
Key words:vienna-type rectifier;single closed-loop strategy;neutral-point potential balance;space vector mo-dulation;carrier modulation;zero-sequence component;pulse width modulation
中图分类号:TM 461
doi:10.3969/j.issn.1000-565X.2015.08.005
文章编号:1000-565X(2015)08-0029-06
作者简介:马辉(1985-),男,博士生,主要从事电力电子功率变换研究.E-mail: mahuizz119@126.com
*基金项目:国家自然科学基金资助项目(61104181)
收稿日期:2014-11-24
Foundation item: Supported by the National Natural Science Foundation of China(61104181)
