并网逆变器的改进型复合控制*

桂存兵　谢运祥　程丽　王裕

(华南理工大学 电力学院, 广东 广州 510640)

并网逆变器的改进型复合控制*

桂存兵谢运祥程丽王裕

(华南理工大学 电力学院, 广东 广州 510640)

摘要：针对低阻尼三阶系统LCL滤波器容易发生谐振的现状，采用并网电流和电容电流双闭环控制策略对并网电流进行控制，并在此基础上设计了采用自适应性改进型内模和插入式结构的重复控制器，同传统的PI控制结合构成新的改进型复合控制，从而提高了其稳定性，减小了入网电流的谐波，提高了并网逆变器的性能.通过仿真和实验验证了所提复合控制方案的可行性与优越性.无论电网电压频率是否变动，该方案都可以在有效避免进网电流谐振的同时实现进网电流的高功率因数.

关键词：LCL滤波器；自适应型内模；改进型重复控制；频率;自适应性

LCL滤波器是一个三阶系统，存在着谐振尖峰,采用并网电流直接闭环控制的并网系统是不稳定的[1].传统抑制谐振尖峰的方法是采用电阻阻尼和有源阻尼.电阻阻尼方法会增加较大的系统功率损耗[2].文献[3-8]中提出的几种有源阻尼方法均需要增加额外的传感器,加大了系统的硬件成本和设计成本.文献[9-10]中采用了间接电流控制方法,通过控制其他电流变量来实现对并网电流的间接控制,难以做到进网电流的单位功率因数.因此需要寻求其他办法消除谐振尖峰.

重复控制具有良好的鲁棒性,稳态时的波形误差为零,但控制上有输出延迟,因而动态响应效果非常差[11].而PI控制的优点是可以立即对动态变化做出响应,缺点是很难做到无静差跟踪.因此将PI控制和重复控制两种控制方法结合在一起,形成一种新的兼具良好稳态和动态性能的复合控制成为一种可选方案.

1逆变器模型

文中所采用的全桥逆变器拓扑结构如图1所示.

图1　全桥并网逆变器主电路图Fig.1　Main circuit diagram of full bridge inverter

忽略其中的寄生电阻，LCL滤波器参数为L1=3.3 mH,C=5 μF,L2=2 mH,直流侧输入电压Udc=400 V[12].

加入电网电压前馈控制后的电流双闭环的结构控制框图如图2所示.图中KPWM=400,为逆变桥等效电压放大系数；i2ref为入网参考电流；k为电容电流内环调节器；i1为逆变器输出电流；i2为入网实际电流；L1、C、L2为LCL滤波器的等效电感和电容.由图2可得电流内环的传递函数为

(1)

图2　双闭环电流控制框图Fig.2　Blockdiagramofdoubleclosed-loopcurrentcontrolsystem

其开环传递函数特征方程阻尼系数为

(2)

取阻尼系数为[13]:ζ=0.707,可求得

K=0.147 84

(3)

由式(1)、(3)可得

(4)

取采样频率为10kHz,采用零阶法离散化可得:

(5)

采用PI调节器实现反馈校正后系统的开环传递函数为Ⅱ型系统:

(6)

采用“振荡指标法”[14]可得:Kp=0.5,Ki=1 000,零阶法离散化可得

(7)

将各系数代入式(6)可得并网电流同参考电流之间的开环传递函数为

(8)

采用零阶法离散化可得

(9)

(10)

其伯德图如图3所示.

由图3可知LCL滤波器的谐振尖峰被有效消除,保证了系统的稳定性.

图3　双闭环控制的离散开环系统伯德图Fig.3　Discreteopen-loopsystemBodediagramofdoubleclosed-loopcontrolsystem

2重复控制器设计

2.1　控制器结构

如图4所示,重复控制器采用插入式结构，与传统的PI控制相结合[15]既可快速响应指令突变,又能实现良好的跟踪性能,从而使被控量具有优良的动态和静态性能.

图4　复合型重复控制结构框图Fig.4　System block diagram of composite repetitive control

图4中P(z)为原系统模型，S(z)为补偿器.

2.2　补偿器

可设补偿器为[11]

S(z)=krzkF1(z)F2(z)

(11)

式中,kr为重复控制增益,根据实际情况设计,调试中可先设置为1.zk补偿滤波器S(z)PI(z)z-1P(z)的相位滞后.F1(z)和F2(z)的作用是使得校正后的S(z)PI(z)z-1P(z)函数在中低频增益为0 dB,同时抵消高频段可能存在的谐振峰值,增强高频衰减,以提高稳定性和鲁棒性.

2.2.1平均值滤波器的设计

文中采用的平均值滤波器表达式为

(12)

平均值滤波器的频率特性响应曲线如图5所示,由图可以看出，其频率特性能满足不改变低频衰减而增加高频衰减的要求.此外,该滤波器为一阶系统,数字实现简单,不需要额外的存储空间.

图5　平均值滤波器伯德图Fig.5　Bodediagramofaveragevaluefilter

2.2.2二阶低通滤波器的设计

二阶低通滤波器的连续域数学表达式为

(13)

设计系统截止频率为2 kHz,阻尼比取0.707,系统采样频率为10 kHz,并采用零阶保持离散化得

(14)

二阶低通滤波器的频率特性响应曲线如图6所示.

图6　二阶低通滤波器伯德图Fig.6　Bodediagramoftwoorderlowpassfilter

(15)

2.2.3超前环节的确定

通过对系统伯德图相位延时的分析,采取凑试法,选取超前2拍,即k=2.因此,补偿器设计为

S(z)=z2F1(z)F2(z).

2.3　Q(z)的设计

Q(z)通常选取为稍小于1的常数或者用LPF替换.这两种方法都偏离理想重复控制内模,降低了系统的性能,尤其是N1为非整数的情况下[16].因此文中采用一种新的Q(z)以提高对电网频率变化的自适应性,即让Q(z)在中低频段逼近或替代z-D,其中D=N1-N,为频率比的小数部分,N为整数部分.

由于采样频率很高,ωTs接近于0,则

(16)

(17)

∠([1-D)+DZ-1]=[(1-D)+Dcos(ωTs)-jDsin(ωTs)

(18)

由式(16)-(18)可推出:

∠z-D≅∠[(1-D)+Dz-1]

(19)

因此,取Q(z)=(1-D)+Dz-1在中低频段能够逼近于延时环节,文中采用的重复控制内模逼近于理想重复控制内模.

3仿真与实验

3.1　仿真比较

为验证理论分析的正确性和单电流双闭环控制系统的稳定性及动态性能,在Matlab的Simulink仿真环境下进行仿真,给定电流均为80A.其中图7、8的电网频率为50 Hz.图9、10的电网频率为49.7 Hz.

图7　基准频率下单PI控制时的波形Fig.7　Single PI control waveforms under the reference frequency

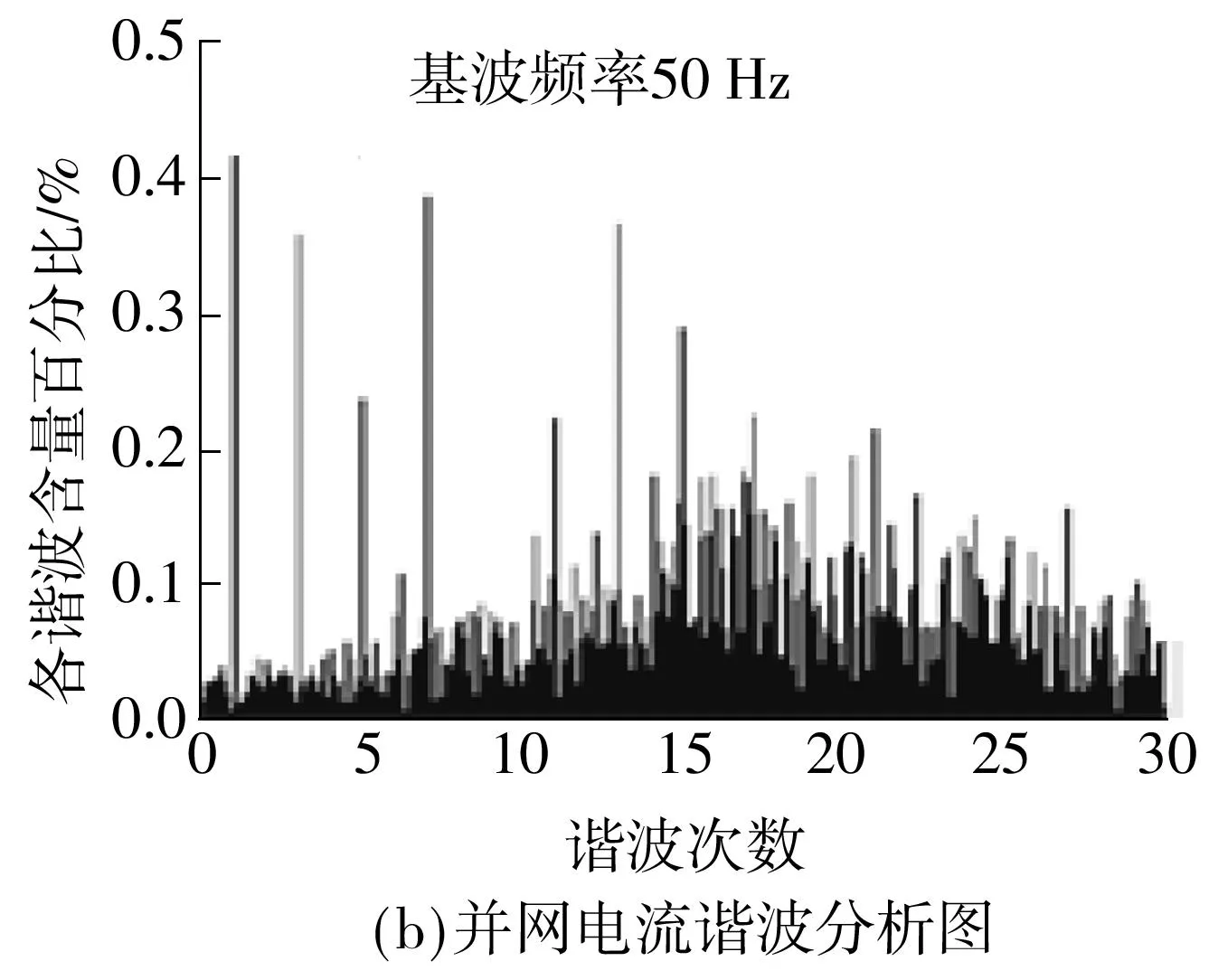
图8　基准频率下普通型复合控制的波形Fig.8　Normal composite control waveforms under the reference frequency

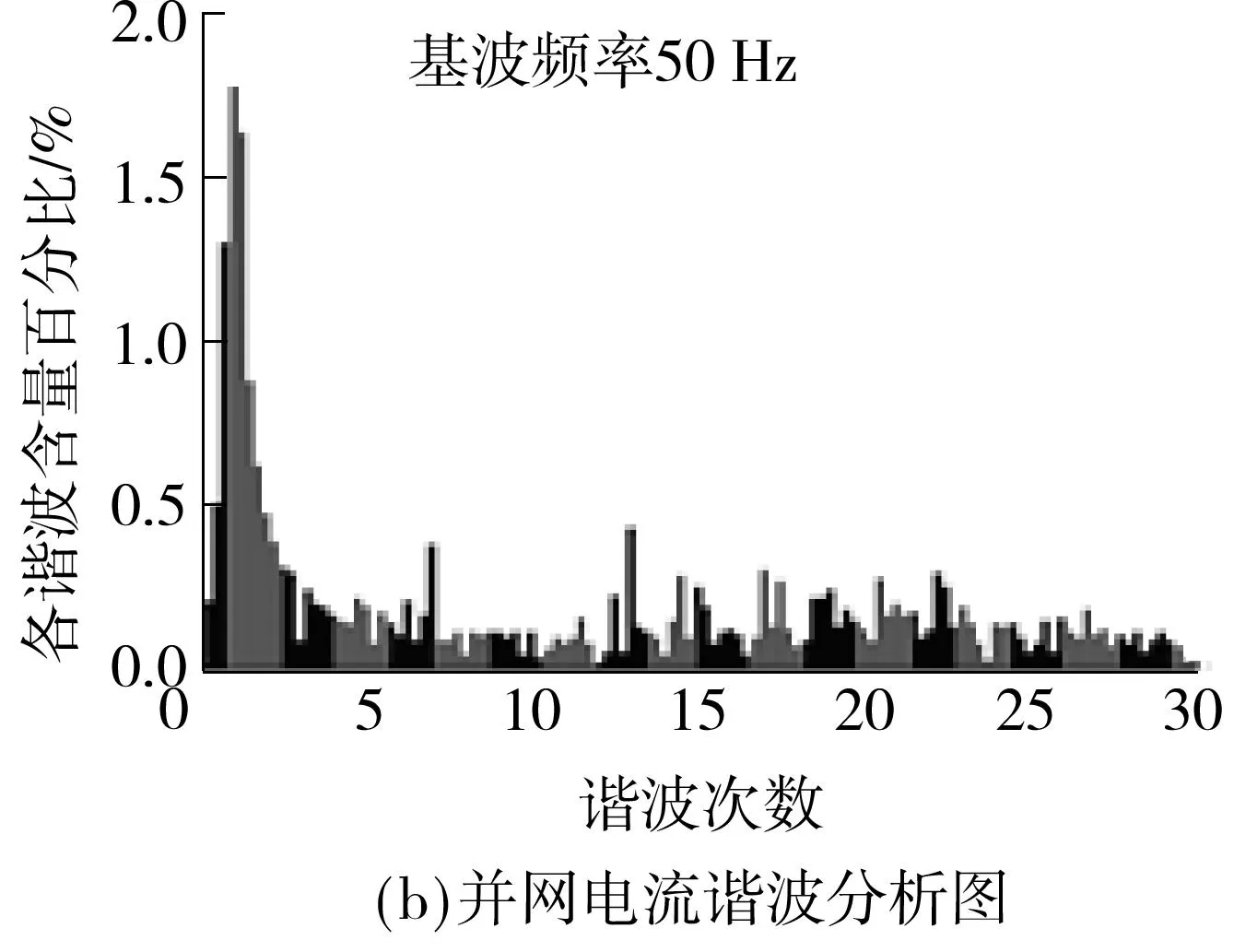
图9　非基准频率下普通型复合控制的波形Fig.9　Normal composite control waveforms under non-reference frequency

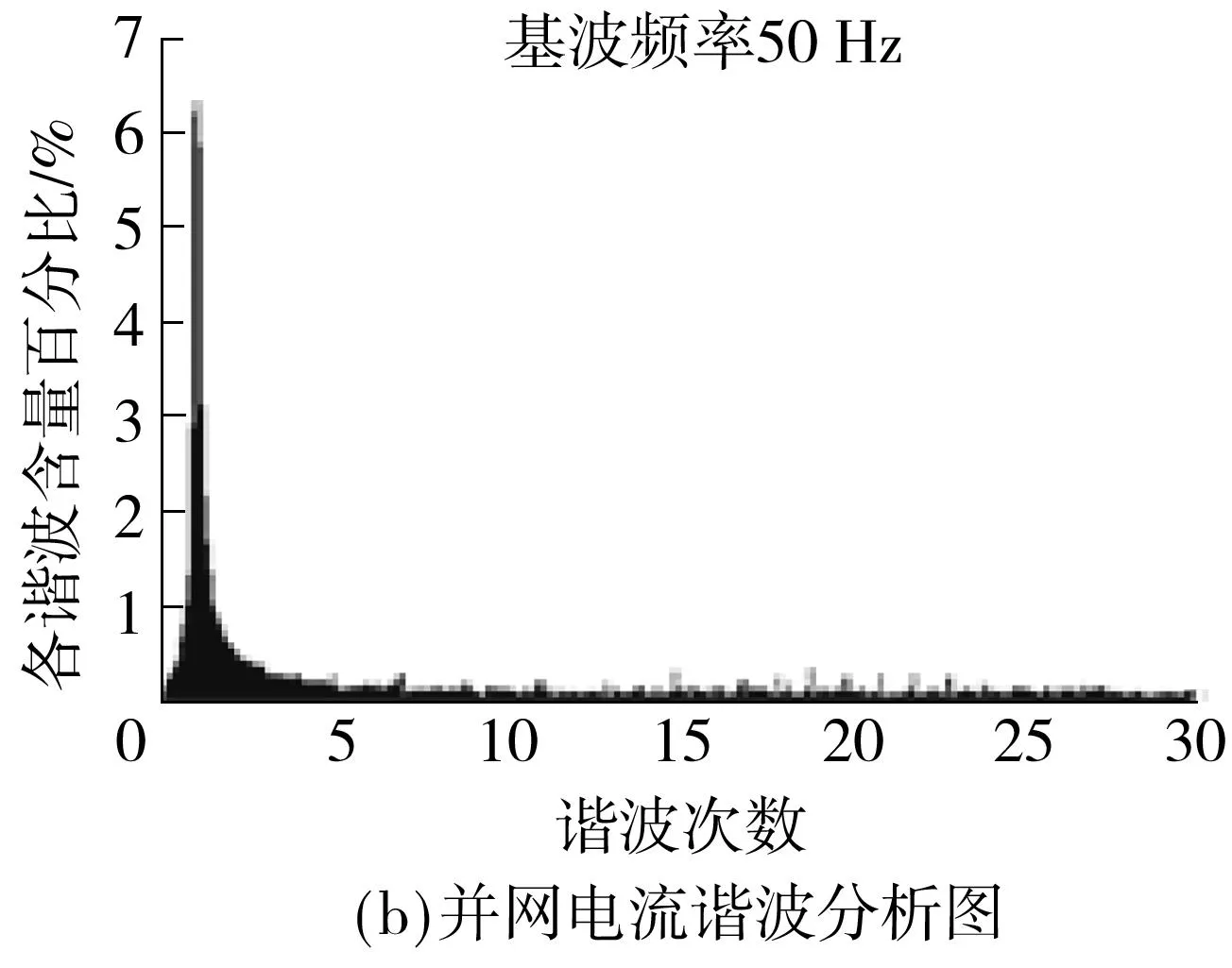
图10　非基准频率下改进型复合控制的波形Fig.10　Modified composite control waveforms under non-refe-rence frequency

3.2　实验验证

为验证理论分析的正确性,搭建了一台LCL并网逆变器实验样机.分别采用普通型复合控制和改进型复合控制,电网频率为51.2 Hz.其实验波形分别如图11和12所示.

由图11和12可见，入网电流的谐波明显减小,稳定性和动态特性得到了提高,采用普通型复合控制时,并网电流THD为1.519%,功率因数PF为0.98;而采用改进型复合控制时,并网电流THD为0.975%,功率因数PF为0.99.很明显改进型复合控制效果优于普通型复合控制,说明改进型复合控制对电网频率变化具有自适应性.

图11　普通型复合控制波形Fig.11　Waveforms under normal composite control

图12　改进型复合控制波形Fig.12　Waveforms under modified composite control

4结语

为增加系统稳定性,采用并网电流和电容电流双闭环控制策略对并网电流进行控制,为了进一步提高其稳定性,设计了一种新型重复控制器.该策略吸取了PI控制和自适应重复控制的长处,克服了它们各自的不足.仿真和实验结果证明,基于PI控制和自适应重复控制的复合控制策略是一种实用的并网逆变器控制方案,该控制策略有效抑制了谐振尖峰,增强了系统稳定性,系统具有优良的动静态性能,而且该方案简便易行.

参考文献：

[1]Twining E,Holmes D G.Grid current regulation of a three-phase voltage source inverter with an LCL input filter [J].IEEE Transactions on Power Electronics,2003,18(3):888-895.

[2]王要强,吴凤江,孙力,等.阻尼损耗最小化的 LCL滤波器参数优化设计 [J].中国电机工程学报,2010,30(27):90-95.

Wang Yao-qiang,Wu Feng-jiang,Sun Li,et al.Optimized design of LCL filter for minimal damping power loss [J].Proceedings of the CSEE,2010,30(27):90-95.

[3]Tang Yi,Loh P C,Wang Peng,et al.Exploring inherent damping characteristic of LCL-filters for three-phase grid-connected voltage source inverters [J].IEEE Trans on Power Electronics,2012,27(3):1433-1443.

[4]Dannehl J,Fuchs F W,Hansen S,et al.Investigation of active damping approaches for PI-based current control of grid-connected pulse width modulation converters With LCL filters [J].IEEE Trans on Industry Applications,2010,46(4):1509-1517.

[5]彭双剑,罗安,荣飞,等.LCL滤波器的单相光伏并网控制策略 [J].中国电机工程学报,2011,31(21):17-24.

Peng Shuang-jian,Luo An,Rong Fei,et al.Single-phase photovoltaic grid-connected control strategy with LCL filter [J].Proceedings of the CSEE,2011,31(21):17-24.

[6]徐志英,许爱国,谢少军.采用LCL滤波器的并网逆变器双闭环入网电流控制技术 [J].中国电机工程学报,2009,29(27):36-41.

Xu Zhi-ying,Xu Ai-guo,Xie Shao-jun.Dual-loop grid current control technique for grid-connected inverter using an LCL filter [J].Proceedings of the CSEE,2009,29(27):36-41.

[7]王要强,吴凤江,孙力,等.带 LCL 输出滤波器的并网逆变器控制策略研究 [J].中国电机工程学报,2011,31(12):34-39.

Wang Yao-qiang,Wu Feng-jiang,Sun Li,et al.Control strategy for grid-connected inverter with an LCL output filter [J].Proceedings of the CSEE,2011,31(12):34-39.

[8]许津铭,谢少军,肖华锋.LCL 滤波器有源阻尼控制机制研究 [J].中国电机工程学报,2012,32(9):27-33.

Xu Jin-ming,Xie Shao-jun,Xiao Hua-feng.Research on control mechanism of active damping for LCL filters [J].Proceedings of the CSEE,2012,32(9):27-33.

[9]张强, 张崇巍, 张兴,等.风力发电用大功率并网逆变器研究 [J].中国电机工程学报,2007,27(16):55-59.

Zhang Qiang,Zhang Chong-wei,Zhang Xing,et al.Study on grid-connected inverter used in high-power wind generation system [J].Proceedings of the CSEE,2007,27(16):55-59.

[10]沈国桥,徐德鸿.LCL 滤波并网逆变器的分裂电容法电流控制 [J].中国电机工程学报,2008,28(18):36-41.

Shen Guo-qiao,Xu De-hong.Current control for grid-connected inverters by splitting the capacitor of LCL filter [J].Proceedings of the CSEE,2008,28(18):36-41.

[11]谢川,张靖.适于重复控制固定采样点数的数字锁相方法 [J].浙江大学学报:工学版,2011,45(5):789-793.

Xie Chuan,Zhang Jing.Digital PLL with fixed number of sampling points for repetitive control algorithm [J].Journal of Zhejiang University:Engineering Science,2011,45(5):789-793.

[12]Lee K J, Park N J, Kim R Y, et al.Design of an LCL filter employing a symmetric geometry and its control in grid-connected inverter applications [C]∥IEEE PESC.Greece:Rhodes,2008.

[13]陈东,张军明,钱照明.带 LCL 滤波器的并网逆变器单电流反馈控制策略 [J].中国电机工程学报,2013,33(9):10-16.

Chen Dong,Zhang Jun-ming,Qian Zhao-ming.Single current feedback control strategy for grid-connected inverters with LCL filters [J].Proceedings of the CSEE,2013,33(9):10-16.

[14]陈伯时.电力拖动自动控制系统:运动控制系统 [M].北京:机械工业出版社,2003:56-76.

[15]秦喆, 苏建徽,刘骏亚,等.一种新型并网逆变器重复电流控制策略的研究 [J].低压电器,2013,11:32-36.

Qin Zhe,Su Jian-hui,Liu Jun-ya,et al.Research of a novel control method for repetitive current control of grid-connected inverter [J].Low Voltage Apparatus,2013,11:32-36.

[16]Zhou Ke-liang,Wang D.Digital repetitive controlled three-phase PWM rectifier [J].IEEE Transactions on Power Electronics,2003,18(1):309-316.

[17]王晓刚, 谢运祥,帅定新,等.基于模型预测控制的三相四桥臂有源电力滤波器 [J].华南理工大学学报:自然科学版，2009,37(11)：56-63.

Wang Xiao-gang,Xie Yun-xiang,Shuai Ding-xin,et al.Three-phase four-leg active power filter based on model predictive control [J].Journal of South China University of Technology:Natural Science Edition,2009,37(11):56-63.

Improved Composite Control of Grid-Connected Inverter

GuiCun-bingXieYun-xiangChengLiWangYu

(School of Electric Power,South China University of Technology,Guangzhou 510640,Guangdong,China)

Abstract:The LCL filter is a third-order system of a low damping, where resonanceis easy to occur.Aiming at the issue,this paper adopts a dual-loop control strategy with the grid-connected current feedback and the capacitor current feedback to control the grid-connected current,and then designs a novel repetitive controller,which possesses a modified self-adaptive internal model and is plugged in the system.This repetitive controller is combined with the traditional PI control to form a new improved composite control scheme,thus improving the working stability of the LCL filter,minimizing the current harmonic distortion and increasing the performance of the grid-connected inver-ter. Finally, the feasibility and superiority of the improved scheme are verified by simulations and experiments. Besides,whether the voltage frequency of power systems changes or not,the improved scheme can effectively avoid the resonance of grid currents and can achieve a high in-grid power factor.

Key words:LCL filter;a modified self-adaptive internal model;modified repetitive control;freguency;adaptability

中图分类号：TM 46

doi:10.3969/j.issn.1000-565X.2015.08.003

文章编号：1000-565X(2015)08-0015-06

作者简介：桂存兵(1974-),男,博士,副教授,主要从事电力电子技术在电力系统中的应用研究.E-mail: ahui200491@126.com

*基金项目：广东省教育部产学研结合项目(2011B090400136)

收稿日期：2014-09-29

Foundation item: Supported by the Project of Integration of Industry,Education and Research of Guangdong Province and Ministry of Education of China(2011B090400136)