改进的基于结构约束的发电机聚合参数解析方法*
2015-02-18朱林李莎刘平武志刚
朱林 李莎,2 刘平 武志刚
(1.华南理工大学 电力学院, 广东 广州 510640; 2.广东电网有限责任公司 电力科学研究院, 广东 广州 510080)
改进的基于结构约束的发电机聚合参数解析方法*
朱林1李莎1,2刘平1武志刚1
(1.华南理工大学 电力学院, 广东 广州 510640; 2.广东电网有限责任公司 电力科学研究院, 广东 广州 510080)
摘要:提出了一种改进的发电机聚合参数解析求解方法.该方法首先通过加入等价移相变压器消除同调发电机合并至公共母线所带来的电压偏差,然后基于发电机结构的系数矩阵不变特性,利用发电机聚合前后在同步平面各轴系投影分量相等的特点,直接获取等值发电机模型参数.文中方法能弥补传统的基于频域传递函数拟合和时域仿真优化的方法对工作点设置或寻优方向选取的依赖性,对发电机模型具有更强的适应性,更可应用于在线计算.
关键词:动态等值;发电机聚合;结构约束;电力系统稳定性
电网动态等值可大幅度化简原系统规模,同时尽可能保持原有的动态特征,已成为研究大电网的一项重要工具[1-4].发电机聚合是电网动态等值中的核心工作,直接影响动态等值结果的精确程度[5-6],因而受到了广泛关注.
近些年来,基于同调等值的动态聚合在发电机聚合方法研究中占有重要地位[7],可以大致分为经典聚合、详细聚合和寻优聚合3种形式[8-9].经典聚合的常见思路是加权求和,例如基于容量权重求取发电机参数,但要求等值前后的发电机模型具有相同的结构形式[10].然而在实际电网中,发电机的模型、参数存在较大差异,该方法的实用性受到较大限制.
详细聚合则是对发电机电磁回路及其控制系统(励磁系统、调速器等)进行聚合[11-12].文献[13-14]中运用一种基于时域下模型系数矩阵结构不变的4阶发电机模型聚合方法,但忽略了同调机群的机端电压幅值与相角差异性,在大规模电网下的聚合效果并不乐观,也缺少对实际系统中广泛采用的5阶或6阶模型的详细讨论.
寻优聚合则是围绕等值机传递函数与待聚合发电机传递函数的频率响应偏差最小这一优化目标,选择不同的优化算法,从而得到等值发电机的参数[15-16].但该方法也存在耗时长、运行效率低、具有不确定性、易陷入局部最优的缺点.文献[17]中比较了加权平均法和频域寻优法两种聚合方法,研究表明频域寻优法的精度更高,但对工作点设置、寻优方向选取有一定依赖性.此外,也有学者提出了内节点聚合、参与因子聚合法,但也难以满足大规模复杂电网对发电机聚合精度与效率的综合要求[18].
针对上述问题,文中提出了一种改进的基于结构约束的发电机聚合解析方法,它精确考虑了将各同调机组移到假想公共母线上时所产生的复变比的影响.该方法利用了结构约束所带来的时域系数矩阵不变特性,在聚合条件下要求等值前后电网注入功率不变,同调机组和等值机的电流相量通过相应的坐标变换在同步平面的D轴和Q轴上投影相等,从而以非迭代方式直接获得了等值机参数.
文中所提方法弥补了传统频域求解方法对工作点设置、寻优方向选取的依赖性,计算效率高,同时也对发电机的各阶模型具有良好的适应性,可应用于复杂大电网的等值化简工作.
1考虑结构约束的发电机聚合
1.1 聚合条件
发电机聚合通常是指将具有相似物理特征的若干台发电机移至一条公共母线上(如图1所示),然后用一台等值机代替的过程.

图1 公共母线化简Fig.1 System after coherency bus elimination
a1~am表示移相变压器复变比
上述替换过程必须满足下述条件要求:
(1)满足恒等功率变换,即等值发电机注入网络的功率与待聚合发电机注入网络功率之和相等;
(2)具有相同动态特性,即待聚合发电机群具有相似的特性(慢同调),在相同扰动下对保留区域的暂态影响一致[19].
1.2 移相变压器的消去
由恒等功率变换,若将待聚合发电机移至公共母线必须首先考虑电压上的差异.此前的研究中多采用理想变压器消除电压幅值差异,但在实际等值过程中会存在待聚合发电机之间电气距离上的差异,因此不仅需要考虑电压幅值的影响,而且还应计及电压角度的因素.
文中考虑了消去移相变压器时电压幅值的影响,为消除电压角度偏差,在待聚合发电机机端和公共母线上加入了一个移相变压器,然后才能进行功率合并,一种可行的处理方法是将其等值为图2(b)所示电路.为保证两端电压、电流无稳态偏差,需要新增节点对地导纳,其数值可根据等值前后保留系统稳态偏差为零这一条件计算获得:
(1)
(2)
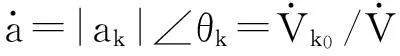

图2 移相变压器等值电路图Fig.2 Diagramofphaseshifttransformerelimination
通过该处理方法,既满足了恒等功率变换的要求,又精确考虑了将各同调机组移到假想公共母线上时所产生的复变比的影响.仅需要在系统导纳阵中修正相应端点的对地导纳,不会增加整个聚合过程的计算量.
1.3 发电机聚合思路
经过上一小节的处理后,待聚合发电机群和等值机之间会具备相同公共母线.待聚合发电机群与等值机要具有相同的动态特性,故在聚合前后母线电压相同的条件下,聚合前后总注入电流也应不变.这是进行发电机聚合的一项核心特征.
在暂态稳定仿真中发电机模型由4、5及6阶形式的微分-代数方程组描述,也可转换成矩阵形式来表达.以标准4阶模型为例:
(3)
(4)
(5)

由式(4)、(5),对待聚合机群中的第k台机有

(6)
写成矩阵形式,可有
Ik=AkVk-AkEk
(7)
类似地,待聚合机群合并为一台等值机,那么等值机也必须有相似的结构形式,即有
Ie=AeVe-AeEe
(8)
由于聚合前后总注入电流不变,在选择同步坐标平面DQ后,聚合发电机群在该平面电流投影之和应与等值机在该平面电流投影相等.待聚合机群中第k台发电机在坐标系下的电流可表示为
IDQk=TkAkVdqk-TkAkEdqk
(9)
式中,VDQk=TkVdqk,定义Tk为各台机从各自的(dk,qk)坐标平面变换到公共坐标平面(D,Q)的坐标变换矩阵,其转换关系如图3所示,
(10)
式中,δk为第k台机q轴超前Q轴的角度,故
(11)

图3 坐标系的转换关系Fig.3 Transformation relations of reference frames
DQ坐标平面的等值机电流是各待聚合发电机的注入电流之和,即有

(12)

可有
(13)
(14)
利用系数矩阵Ae的结构特点,可相应求解出直轴、交轴上的电气物理量.等值机具体参数的推导将在下一节中重点展开.
2等值机参数推导
2.1 惯性时间常数M*和阻尼系数D*
由同调待聚合发电机转速相同,利用转子运动方程,易得
(15)
式中,Mk和Dk分别为第k台机的惯性时间常数和阻尼系数.
2.2 同步电抗和
比较式(8)和式(13),有
(16)
由系数矩阵Ae的表达形式可得等值同步电抗:
(17)
系数矩阵中的元素求解可参见文后附录.
2.3 暂态电抗和

(18)
2.4 次暂态电抗和
该组参数用于发电机5阶、6阶实用模型中.参考上一节中4阶模型形式,可将定子电压方程化为相同结构形式:
(19)
同理,利用相同的聚合条件与坐标变换矩阵,比较相应的系数矩阵A″e,即可获得对应参数:
(20)
2.5 暂态时间常数D0和
由式(3)和(5),第k台机的模型可描述为
(21)
写成矩阵形式,有

(22)
对等值机,有
(23)
(24)
2.6 次暂态时间常数T和T
由次暂态电抗表示的同步电机稳态方程,
(25)
利用相同的聚合条件与坐标变换矩阵比较相应的系数矩阵C″e,得

(26)
从等值机的参数推导过程可以看出,文中所提的算法充分利用了发电机的聚合条件,在结构特征相同的约束下,通过坐标平面变换直接求取等值机参数.同时,算法对待聚合发电机模型具有良好的适应性,可广泛适应于4阶至6阶模型,并不依赖于具体的寻优算法和工作点设置,整体计算量小,可在线应用.
3案例分析
3.1 仿真案例1
为检验文中方法有效性,选用图4所示的新英格兰10机39节点系统进行仿真.通过同调判别把系统中的发电机划分为4个区域,用文中所提方法仅对区域3中编号G33至G36的4台发电机进行聚合,等值前后的发电机参数如表1所示.

图4 新英格兰39节点系统图Fig.4 New England 39-bus system
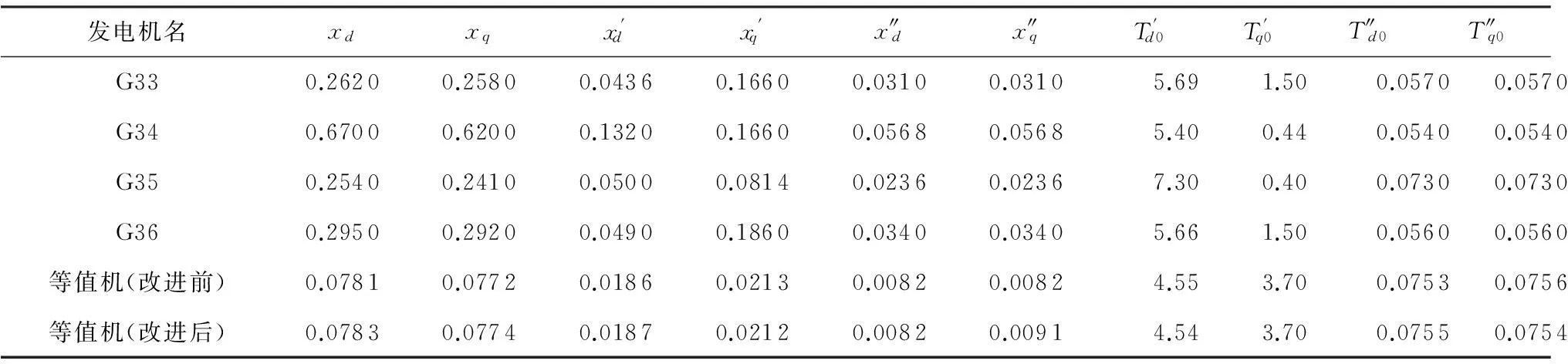
表1 发电机G33-G36与等值机参数Table 1 Parameters of G33-G36 and their equivalent generators
在该系统中,12号母线处设置三相瞬时短路故障,0.1 s后故障消除.对比进行消去移相变压器时电压幅值影响的改进前后的聚合效果,发电机G33-G36与对应等值机的功角曲线及端电压曲线分别如图5和6所示.图6中电压为标幺值,可见,等值机表现出了与发电机G33-G36的相似动态性能,发电机同调分组方案合理.
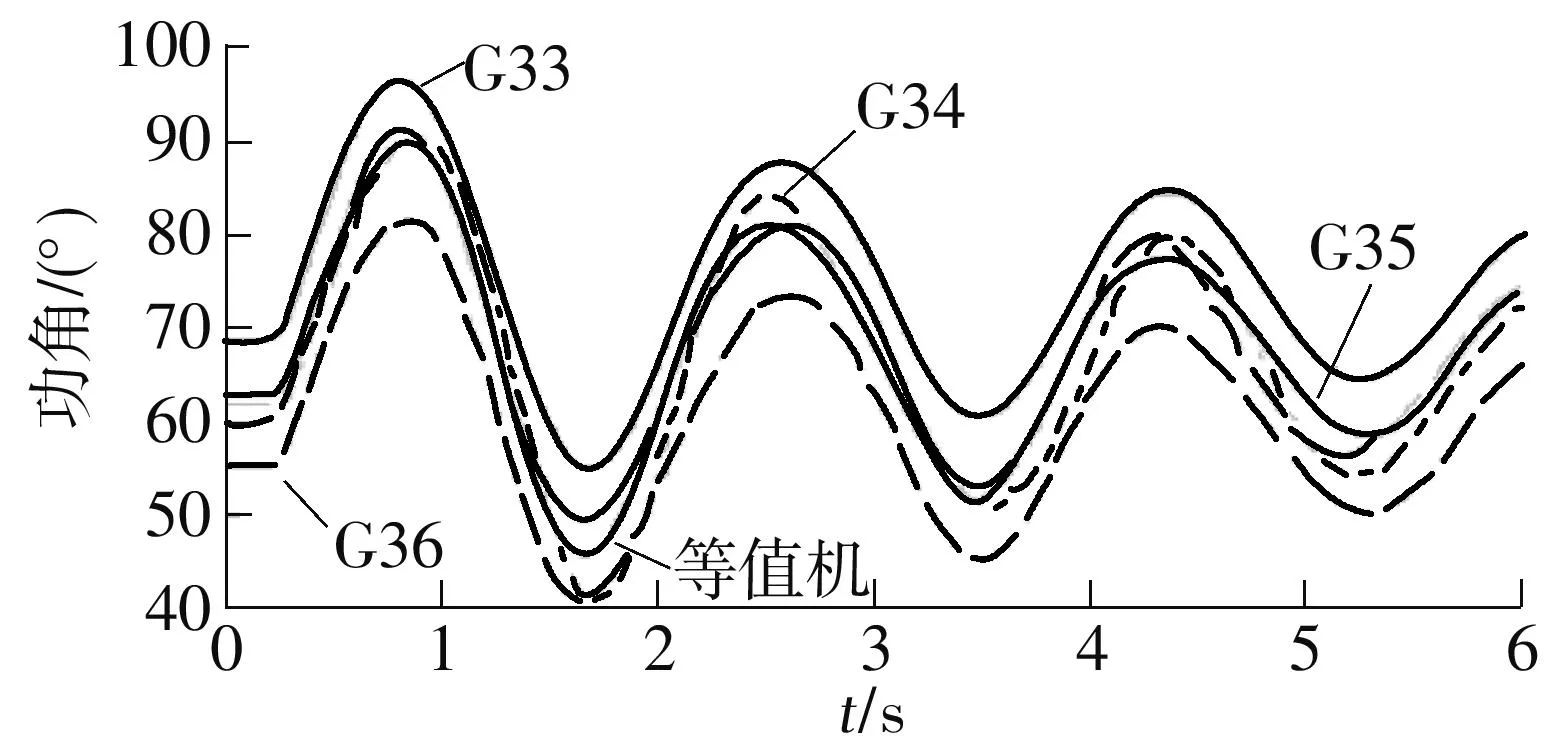
图5 发电机及其等值机功角曲线Fig.5 Rotor curves of coherent groups and their equivalent
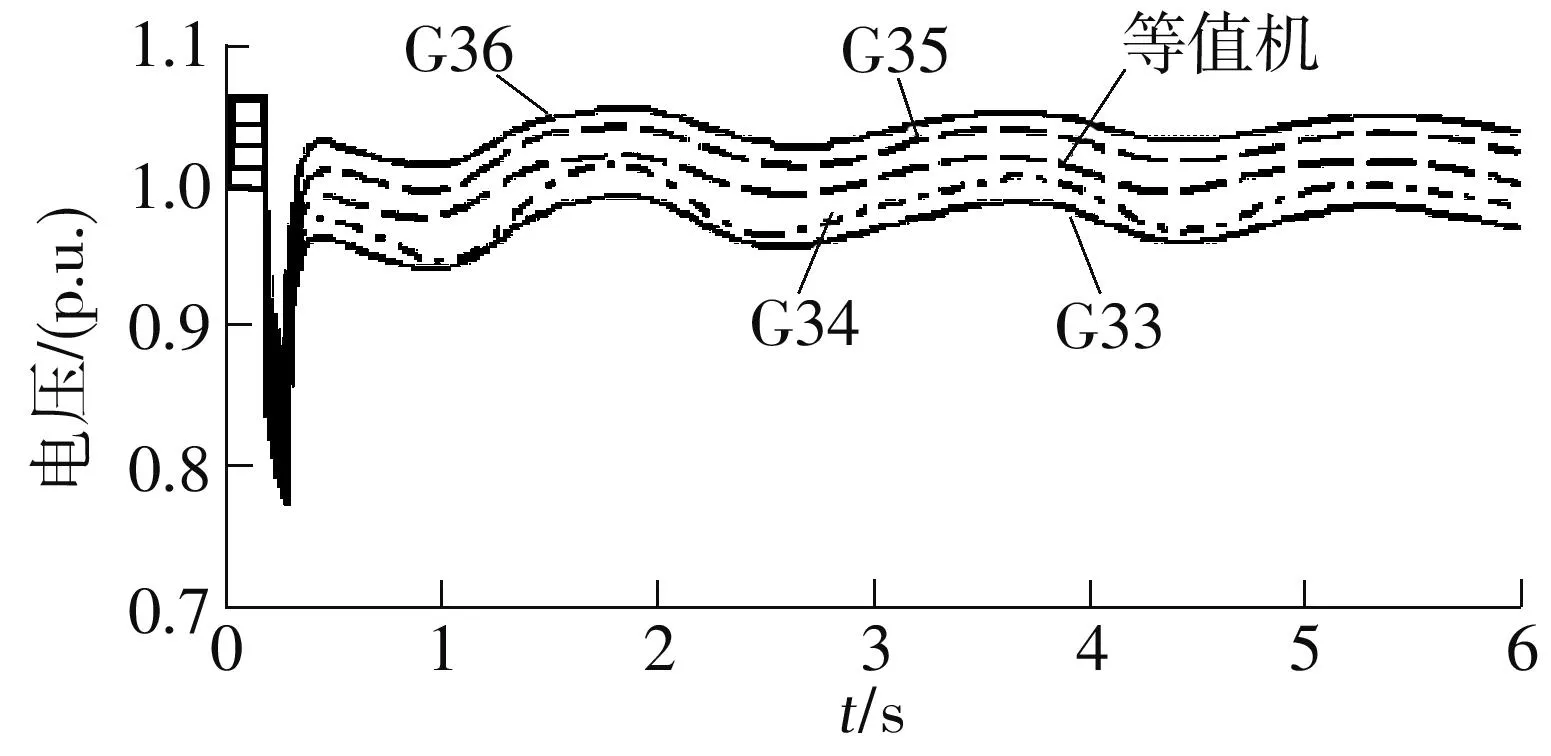
图6 发电机群与等值机的电压曲线Fig.6 Voltage curves of coherent groups and their equivalent
为校验等值机是否能较好地替代原机群,还需要进一步考察保留节点和保留线路上的暂态过程.发电机G32为系统保留发电机且靠近故障点,其在原始系统和等值系统中的功角曲线如图7所示.故障点处的电压(节点12)与附近的线路(节点11-12)功率曲线分别如图8和9所示.
由上述仿真曲线可见,文中所提算法在新英格兰39节点系统中效果良好,解析聚合方法改进后较改进前有更为相似的动态特性,获得的等值机能更良好地反应原机群的动态特性,具有更高的等值精度.

图7 发电机G32功角曲线Fig.7 Rotor curves of generator G32

图8 故障点处母线电压Fig.8 Voltage curves at fault bus

图9 线路11-12上的有功功率Fig.9 Active power curves at line 11-12
3.2 仿真案例2
将文中方法用于更大规模的实际系统检验其有效性.选取南方电网某年的典型运行方式数据(1918节点,510台发电机),将其化简为规模更小的网络(1243节点,103台发电机).原系统中的发电机划分为40个同调机群,并选用传统的寻优法与文中方法进行效果对比.两种算法获得的同调机群等值机参数如表2所示.

表2 同调机群等值机参数Table 2 Parameters of coherent equivalent generator
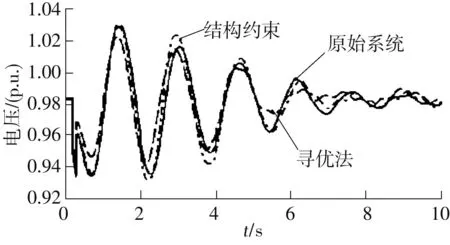
图10 525 kV罗洞母线电压曲线Fig.10 Voltage curves of 525 kV Luodong bus
在安顺至高坡的500 kV线路上设置三相短路故障,0.2 s后故障清除.观测故障附近的节点电压、线路功率变化情况,如图10和11所示.可以看出,文中所提出的算法较传统的寻优方法在聚合效果上有进一步的改善,所得到等值系统能更好地反应原始系统受扰后的振荡趋势.

图11 梧罗甲线有功功率曲线Fig.11 Active power curves of Huizhou to Luodong line I
4结语
提出了一种改进的发电机聚合参数解析求解方法,即通过加入等价移相变压器消除同调发电机合并至公共母线所带来的电压偏差,在聚合条件要求下,充分利用发电机结构的系数矩阵和发电机聚合前后在同步平面各轴系投影分量相等的结构特点,直接获取等值发电机参数.与传统的寻优法相比,文中方法计算量小,对发电机模型具有更强的适应性.与传统的解析聚合方法相比,文中方法具有更高的精确度,在新英格兰系统和南方电网某一运行方式下的仿真结果表明了所提方法的有效性.
附录:
(1)惯性时间常数M*和阻尼系数D*的确定
将m台同调机的转子运动方程叠加,可得
(1)
若设等值机运动方程为
(2)
比较附录中的式(1)和(2)得等值机参数.
系数矩阵中的系数可以用实数表示:

(3)
(4)
(5)
因为等值机系数矩阵应与各同调发电机的系数矩阵用相同的结构形式,故Ae11=Ae22=0,得
(6)
由文中式(8)和(13)有
(7)
同理,对暂态求导得
(8)
由文中(25)得到m台同调机的复合模型
(9)
把附录中的式(8)代入附录中式(9),得
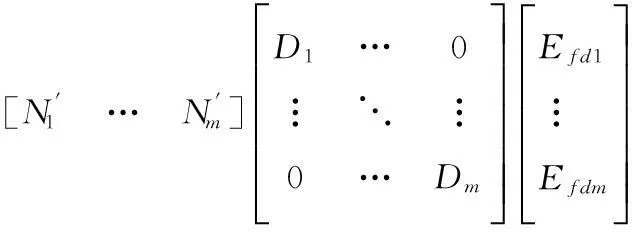
(10)
把附录中的式(7)代入文中式(23),得
(11)
比较附录中的式(10)和(11),得
(12)
(13)
参考文献:
[1]倪以信,陈寿孙,张宝霖.动态电力系统的理论和分析 [M].北京:清华大学出版社,2002.
[2]姚海成,周坚,黄志龙,等.一种工程实用的动态等值方法 [J].电力系统自动化,2009,33(19):111-115.
Yao Hai-cheng,Zhou Jian,Huang Zhi-long,et al.A Practicable method for dynamic equivalence [J].Automation of Electric Power Systems,2009,33(19):111-115.
[3]张宝珍,张尧,凌林雪.基于改进差分进化算法的估计等值法 [J].华南理工大学学报:自然科学版,2014,42(4):7-12.
Zhang Bao-zhen,Zhang Yao,Lin Ling-xue.Estimation equivalence method based on modified differential evolution algorithm [J].Journal of South China University of Technology:Nature Science Edition,2014,42(4):7-12.
[4]彭伟,徐泰山.电力系统动态等值中发电机的选择方法 [J].电力系统自动化,2010,34(14):48-52.
Peng Wei,Xu Tai-shan.A generator selection method for power system dynamic equivalents [J].Automation of Electric Power Systems,2010,34(14):48-52.
[5]胡杰,余贻鑫.电力系统动态等值参数聚合的实用方法 [J].电网技术,2006,30(24):26-30.
Hu Jie,Yu Yi-xin.A practical method of parameter aggregation for power system dynamic equivalence [J].Power System Technology,2006,30(24):26-30.
[6]张宝珍,张尧,林凌雪,等.基于PSO-FCM算法的同调发电机识别 [J].华南理工大学学报:自然科学版,2013,41(4):8-13.
Zhang Bao-zhen,Zhang Yao,Lin Ling-xue,et al.Identification of coherent generators based on PSO-FCM algorithm [J].Journal of South China University of Technology:Nature Science Edition,2013,41(4):8-13.
[7]Marinescu B,Mallem B,Rouco L.Large-scale power system dynamic equivalents based on standard and border synchrony [J].IEEE Transactions on Power Systems,2010,25(4):1873-1882.
[8]刘丽霞,罗敏,李晓辉,等.电力系统常用动态等值方法的比较与改进 [J].电力系统及其自动化学报,2011,23(1):149-154.
Liu Li-xia,Luo Min,Li Xiao-hui,et al.Comparison and improvement of common methods of dynamic equivalence in power system [J].Proceedings of the CSU-EPSA,2011,23(1):149-154.
[9]Zin A A M,Kok B C,Mustafa M W,et al.Time domain dynamic aggregation of generating unit based on structure preserving approach [C]∥Proceeding of the Power Engineering Conference.Bangi:IEEE,2003:154-160.
[10]Zhang Bao-zhen,Zhang Yao,Liao Ming-yang,et al.Study on dynamic equivalent coherency-based of Hainan power grid [C]∥Proceeding of IEEE Asia-Pacific Power and Energy Engineering Conference.Washington DC:IEEE Computer Society,2012:1-4.
[11]Nath R,Sc B,Lamba S S.Development of coherency-based time-domain equivalent model using structure constraints [J] Proceeding of IEE Generation,Transmission and Distribution,1986,133(4):165-175.
[12]Ourari M L,Dessaint L A,Do V Q.Generating units aggregation for dynamic equivalent of large power systems [C]∥Proceeding of Power Engineering Society General Meeting.Denver:CO,2004:1535-1541.
[13]Ourari M L,Dessaint L A,Do Van-Que.Dynamic equivalent modeling of large power systems using structure preservation technique [J].IEEE Transactions on Power Systems,2006,21(3):1284-1295.
[14]Yang Yong-bo,Zha Xiao-ming.Time domain aggregation of generating units for shipboard power systems [C]∥Proceeding of Asia-Pacific Power and Energy Engineering Conference.Wuhan:IEEE Power & Energy Society,2009:1-4
[15]孙素琴,蒋周士,周海强,等.电力系统动态等值中原动机调速系统聚合的研究 [J].电力系统保护与控制,2010,38(12):24-28.
Sun Su-qin,Jiang Zhou-shi,Zhou Hai-qiang,et al.Agg-regation of turbine and governing system for dynamic equivalents of power systems [J].Power System Protection and Control,2010,38(12):24-28.
[16]张一荻,管霖.蚁群算法在发电机动态参数聚合中的应用 [J].电力系统保护与控制,2012,40(2):23-27.
Zhang Yi-di,Guan Lin.Application of ant colony algorithm in generator dynamic parameter aggregation [J].Power System Protection and Control,2012,40(2):23-27.
[17]Zhang Bao-zhen,Zhang Yao,Lin Ling-xue,et al.Study on two dynamic aggregation algorithms of coherent ge-nerators [C]∥Proceeding of the Fourth Computational Intelligence and Communication Networks (CICN).Mathura:CPS,2012:676-680
[18]Singh R,Elizondo M,Shuai Lu.A review of dynamic generator reduction methods for transient stability studies [C]∥Proceeding of IEEE Power and Energy Society General Meeting.Detroit:IEEE,2011:1-8
[19]杨靖萍.大规模互联电力系统动态等值方法研究 [D].杭州:浙江大学电气工程学院,2007.
An Improved Analytical Method of Generator Aggregation Parameters Based on Structural Constraint
ZhuLin1LiSha1,2LiuPing1WuZhi-gang1
(1.School of Electric Power,South China University of Technology,Guangzhou 510640,Guangdong,China;
2.Electric Power Research Institute of Guangdong Power Grid Co.,Ltd.,Guangzhou 510080,Guangdong,China)
Abstract:Proposed in this paper is an improved analytical method of generator aggregation parameters. This method first adds a phase shift transformer to a common bus to eliminate the voltage deviation caused by moving coherent generators, and then directly obtains the parameters of the equivalent generating units based on the coefficient matrices structure preservation characteristic of the generator structure and the fact that the sum of the current phasor on every axis of the synchronous planes is equal. This method overcomes the deficiencies of the traditional methods, which depend on the transfer function fitting in the frequency domain or the time domain simulation and thus rely on the setting of working points and the selection of optimization directions. Therefore, the proposed method is more adaptive for generating unitsand can be applied to the on-line calculation.
Key words:dynamic equivalence;generator aggregation; structural constraint;electric power system stability
中图分类号:TM 711
doi:10.3969/j.issn.1000-565X.2015.08.007
文章编号:1000-565X(2015)08-0041-08
作者简介:朱林(1979-),男,博士,副教授,主要从事电力系统稳定与控制研究.E-mail: Zhul@scut.edu.cn
*基金项目:国家自然科学基金资助项目(51407079);国家“863”计划项目(2012AA050209)
收稿日期:2015-01-04
Foundation items: Supported by the National Natural Science Foundation of China(51407079) and the National High-Tech R&D Program of China(863Program)(2012AA050209)
