基于邻接矩阵的公交换乘查询算法设计与实现

孙金华，孟昭睿，谢彦麒

(厦门理工学院计算机与信息工程学院，福建 厦门 361024)



基于邻接矩阵的公交换乘查询算法设计与实现

孙金华，孟昭睿，谢彦麒

(厦门理工学院计算机与信息工程学院，福建 厦门 361024)

摘要：针对公交网络换乘问题，基于有向赋权图构造了公共交通换乘矩阵，设计并实现以换乘次数最少为目标的公交换乘查询算法。在此基础上，构建公交查询系统，用以完成公交线路查询、公交站点查询、公交换乘方案查询等功能。通过实际测试表明，系统能运行于基于Android系统的移动设备，为用户出行带来方便。

关键词：公交换乘算法；最小换乘；换乘矩阵；公共交通网络

0引言

人们搭乘公交之前，希望能获知指定线路有哪些站点，到目的站点该如何换乘等信息，所以研发公交查询系统，特别是能运行于智能手机等移动平台的公交查询系统势在必行。公交查询系统中，最核心的问题是公交换乘问题[1]。目前，对公交换乘问题求解方法主要基于经典的最短路径算法和智能搜索算法，前者如Dijkstra改进算法、Floyd算法等，后者如蚁群算法、A*算法等[2-3]。这些算法要么计算复杂、要么耗时较高，为了适应移动设备运行的需求，本文以换乘次数最少作为设计的首要目标，引入换乘矩阵简化查询过程，提出了基于矩阵运算的公交换乘算法，提高了算法的效率。

1公交网络的抽象

公交车按既定的站点和线路运行停靠，其运行线路具有连通性、节点性和有向性，故可将其视为连通的有向赋权图[4-5]。把公交站点视为“节点”，连接站点间的线路视为“边”，这样公交网络可用有向抽象图G(S，R，M)表示[5-6]。

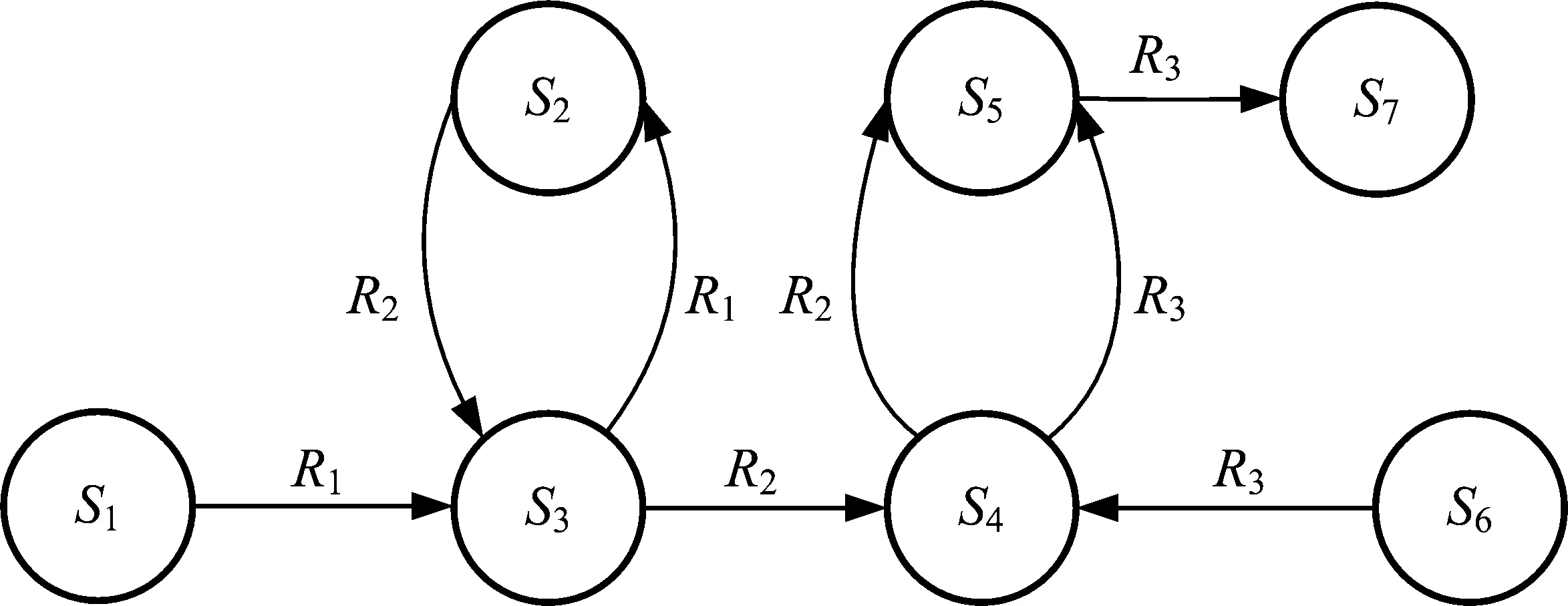
图1　公交网络图

其中，S={Si|i=1,2,…,p}，为公交站点的集合，包括公交网络中的所有站点和可能的线路起止点，对各站点进行唯一编号；R={Rj|i=1,2,…,q}为公交线路集合，各线路给予唯一编号。在此约定，如果是上下行线或往返线路，被当成两条不同的线路，如果是环线，则当成是一条线路；M={Ri|S1,S2,…,Sd}(i=1,2,…,q；d=1,2,…，p),表示为线路/站点关系集合,其元素Ri表示第i条线路依次包含站点S1至Sd，即其运行路线为从起点站S1出发到终点站Sd止。

在抽象图G(S，R，M)中，M本质上描述的是各条公交线路和站点间的关系，引入线路矩阵M′=(mi,j)，其元素mi,j表示Ri路的第j个结点对应的站点序号。公交网络示例如图1所示。

2公交换乘模型

2.1　单条线路的换乘矩阵

假定某市总共有N个公交站点，则任意两个站点之间可否乘坐Ri路公交车到达可由Wi进行描述[7]：

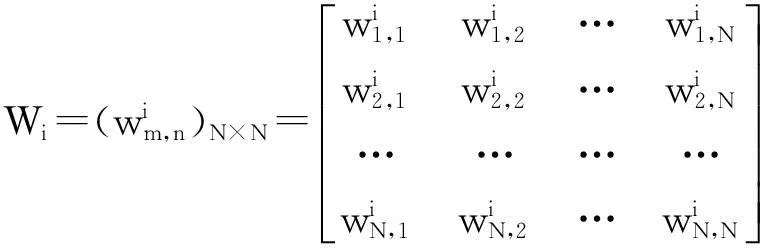
(1)

图1中包含3条公交线路，各自的行程和所经站点如表1所示。将公交线路R1、R2和R3分别转化为对应的矩阵W1、W2和W3可得：

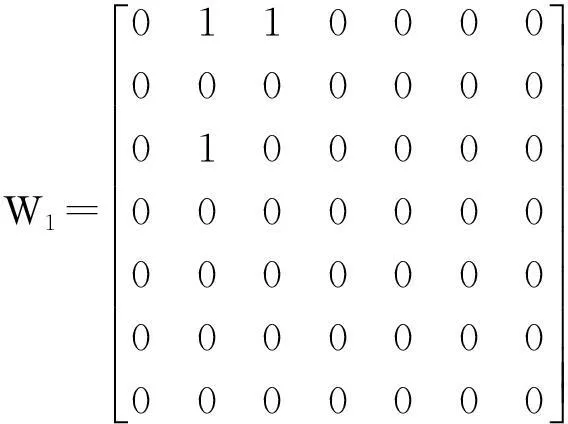
表1　公交线路示例

2.2　整个公交网络的换乘矩阵

假设这个城市总共有T路公交车，则对所有线路的公交换乘矩阵求和，便可得到该城市整个公交网络的换乘矩阵：

(2)

在整个公交网络所对应的换乘矩阵中，如果第m行n列元素δm,n>0，则说明从m站可乘公交车到达n站，其中δm,n值为可选线路数目[7]。

3换乘算法

概括起来，公交换乘问题主要需要解决3个问题： 1)站点间是否可达？2)有哪几路车可达？3)在哪些站点可换乘？

3.1　换乘算法设计

公交换乘算法所涉基础数据包括公交换乘矩阵W和线路矩阵M′，如前所述，这两类矩阵可以根据站点编号和公交线路直接生成。根据前面的理论分析和模型，可设计换乘算法：

输入：起屹站点编号i,j；

输出：从站点i到j途经的公交线路编号；

算法步骤：

Step1:

Flag=0;//Flag,是否找到换乘方案标记

iF(δi,j>0)//δi,j为换乘矩阵W中i行j列元素

{Flag=1;

标记i到终点站j之间可直达；

//Row(i)为线路矩阵M′中i所处的列序号

查找M′包含i和j且Row(i)

输出Lij； //Lij即为线路编号

}

else

gotoStep2;

Step 2://查找一次换乘方案

Flag=0;

For(k=1;k<=N;k++)//N为站点总数

iF(δi,k>0 &&δk,j>0)

{标记k为中转站

Flag=1;

查找M′包含i和k且Row(i)

查找M′包含k和j且Row(k)

输出Lik，Lkj；

}

iF(Flag==0)//没找到一次换乘方案

gotoStep3;

Step 3://查找二次换乘方案

Flag=0;//Flag为是否找到换乘方案的标记

For(k=1;k<=N;k++)

For(t=1;t<=N;t++)

iF(δi,k>0 &&δk,t>0&&δt,j>0)

{标记k,t为中转站

Flag=1;

查找M′包含i和k且Row(i)

查找M′包含k和t且Row(k)

查找M′包含t和j且Row(t)

输出Lik,Lkt,Ltj；

}

iF(Flag==0)

输出没有找到线路的提示信息;

由于城市公交线路通常是经过交通管理部门严格规划的，对中小城市而言，换乘次数一般不会超过2次，因此，算法中只考虑了最多2次换乘的情况，若需3次以上的换乘，方法相似，在此不作详述。

3.2　算法时间性能分析

换乘矩阵W和线路矩阵M′根据公交公司站点和线路直接生成，共中W的规模为n×n，M′的行数目为整个城市的公交线路总数，列数目所有线路中最长线路站点数。初始化完成后，以后的查询无需重新计算。

如果不考虑前期的数据准备和后面的数据输出，算法的运算主要集中在步骤2和步骤3，计算的操作主要是对换乘矩阵W和线路矩阵M′中元素的搜寻。算法步骤1可直接读取判断，时间复杂度为O(1)，步骤2的为O(n)，步骤3的为O(n2)，综合的时间复杂度为O(n2)，其中n为站点数。

对实际应用问题而言，一般城市公交线路数不会很大、站点数也不会非常多。以厦门市公交数据为例，该市现有公交线路297条，不同名公交站点883个。对历史数据的统计表明各类换乘比例为：直达12.6%，1次换乘58.78%,2次换乘27.76%，其他情况0.86%，据此可得厦门市公交平均换乘次数约为1×58.78%+2×27.76%+3×0.86%=1.168 8次。这表明，前述算法实际应用于具体城市数据时，可在接近O(n)的时间内完成，且n值通常小于1 000。

4算法实现与应用

基于前述公交换乘算法，实现了公交查询系统。系统采用C/S结构，其中，后台服务器主要提供公交线路到矩阵转换及相关运算、数据更新等服务。查询系统运行于Android智能手机客户端，核心部分采用离线模式，经服务器处理的换乘矩阵数据存储于手机端SQLite数据库中，采用不定期的一次性从服务器上更新公交站点和线路数据到本地数据库方式更新。

把本文算法应用于实际的厦门市公交网络，在Android 3.2、CPU频率1.1 GHz，内存为512 MB的手机平台下，测试结果显示，查询任意两个站点间的换乘方案，响应时间不超过0.6 s，表明换乘算法能够实现公交换乘方案的查询，是有效的。

5结束语

本文通过对公交网络特征的分析，引进公交线路的邻接矩阵，建立网络的换乘矩阵，用数学的方法有效解决公交换乘问题。将算法实际应用厦门市公交地理数据，可在保证换乘次数最少的情况下，选择公交换乘方案，表明算法是可行有效的，可应用于大多数城市。

参考文献

[1] 杨新苗,王炜,马文腾.基于GIS的公交乘客出行路径选择模型[J].东南大学学报(自然科学版),2000,30(6):87-91.

[2]李孟磊.公交网络模型与出行换乘研究[D].上海：华东师范大学,2011：25-26.

[3]Huang Y,Yi Q,Shi M.An Improved Dijkstra Shortest Path Algorithm[C]//Proceedings oF the 2nd International ConFerence on Computer Science and Electronics Engineering.Paris:Atlantis Press，2013:226-229.

[4]张存保,李华,严新平.基于Web GIS的城市公交问路系统[J].武汉理工大学学报(交通科学与工程版),2004,28 (1):99-102.

[5]姚春龙,李旭,沈岚.公交出行最优路径搜索的有向赋权图模型[J].计算机应用研究,2013，30(4):1058-1063.

[6]郑朝晖.公交网络中最优路径算法的探索[J].太原师范学院学报(自然科学版),2008,7(2):37-43.

[7]续婷,朱烽.基于换乘次数最少的公交查询模型[J].西南民族大学学报(自然科学版)，2010,36 (1):58-62.

Design and Implementation oF Algorithm For Public Transit TransFer

Based on Adjacency Matrix

Sun Jinhua， Meng Zhaorui， Xie Yanqi

(SchooloFComputerandInFormationEngineer，XiamenUniversityoFTechnology，XiamenFujian， 361024)

Abstract:The transFer matrix oF public traFFic network with nodes representing stations and directed arcs showing traFFic routes is presented， transFer matrix and line matrix are introduced to discuss the path-planning problem and the least transFer algorithm is obtained. By applying the transFer matrix theory， we design and realize an urban public transportation query system， which helps to Finish the bus lines and site inquiries and travel line planning， and so on. Tests and applications results show that the system can run on mobile devices based on the Android system， and it is easy For users to travel．

Key words:public traFFic transFer algorithm; minimum transFer; transFer matrix; public traFFic network

中图分类号：TP311

文献标识码：A

文章编号：1001-9146(2015)03-0060-04

作者简介：孙金华(1976-)，男，福建三明人，讲师，计算机软件.

基金项目：福建省教育厅科技计划资助项目(JB12184)

收稿日期：2014-09-11

DOI:10.13954/j.cnki.hdu.2015.03.012