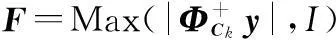基于压缩感知的自适应匹配追踪算法优化

吕伟杰, 陈　霞, 刘红珍

(天津大学电气与自动化工程学院, 天津 300072)



基于压缩感知的自适应匹配追踪算法优化

吕伟杰, 陈霞, 刘红珍

(天津大学电气与自动化工程学院, 天津 300072)

摘要：针对基于压缩感知的稀疏自适应匹配追踪(sparsity adaptive matching pursuit, SAMP)算法运行效率低的问题,给出了一种优化的自适应匹配追踪(modified adaptive matching pursuit, MAMP)算法。该算法在支撑集选择过程中对稀疏度进行了初步估计,并优化了迭代停止的条件。实验表明,该算法相比于SAMP有更快的收敛速度,并且实现更优的重建效果。

关键词：压缩感知; 自适应; 匹配追踪

0引言

压缩感知(compressive sensing, CS)[1-4],自提出以来,在应用数学、计算机科学和电子工程等各个领域已得到了广泛应用。CS理论涉及3个关键问题[5]：稀疏表示、压缩观测和优化重构。重构算法影响CS理论的实用性,因此是其中较为关键的部分。

在重构算法中,贪婪迭代算法的应用最为广泛,这类算法主要包括正交匹配追踪[6]、分段正交匹配追踪(orthogonal matching pursuit, OMP)[7]、规范正交匹配追踪[8]、子空间追踪(subspace pursuit, SP)[9]、压缩采样匹配追踪(compressed sampling matching pursuit, CoSaMP)[10]以及迭代硬阈值法[11]等。这些算法都需要预估稀疏度,为解决这一问题,稀疏自适应匹配追踪[12](sparsity adaptive matching pursuit, SAMP)算法被提了出来。

SAMP依据步长信息逐步扩充支撑集,自适应地完成信号重构。选取的步长越小,重构的精度越高,但同时也会导致重构过程更加繁琐。为此,本文提出了一种优化的自适应匹配追踪(modified adaptive matching pursuit, MAMP)算法,在支撑集选择过程中对稀疏度进行了初步估计,并优化了迭代停止的条件,如此在信号处理过程中,缩短了运行时间,同时又能更精确地重构目标信号。

1CS模型及描述

在CS理论模型中,首先将信号进行稀疏表示,得到稀疏系数,再将其投影到一个合适的观测矩阵上来得到观测向量,并利用观测向量重构原始信号。

CS可描述为：如果离散信号x(N×1),投影到基Ψ=[Ψ1,Ψ2,…,ΨN]上后可表示为

(1)

式中,s为N×1的系数向量,且有K(K≪N)个系数非零,其余系数均为0或非常接近于0; Ψ是N×N的稀疏矩阵。那么,就能使用一个与Ψ不相关的观测矩阵Φ对原信号进行观测,得到观测向量y(M×1)：

(2)

将式(1)与式(2)结合,得

(3)

因观测维数M远小于信号维数N,所以重构面临求解欠定方程组的问题。如果信号x是稀疏的或者可压缩的,则可以转化为最小l0范数问题来求解：

(4)

求解式(4)所描述的优化方程中的最小l0范数优化问题,是一个NP-hard问题,数值计算结果复杂度高,而且极不稳定。文献[13]指出,可通过求解一个更简单的l1范数优化问题来得到同样的解：

(5)

2MAMP算法

2.1SAMP算法

SAMP算法[14],引入步长信息,分段进行,逐步扩充支撑集。在每一段中,都经过预选、候选及剪裁3步,如果残余范数大于上次迭代残余范数,则增大支撑集的大小;否则继续搜索更优支撑集。如此循环,当达到停止迭代条件时,退出循环,此时便得到与目标信号最匹配的原子构成的支撑集。流程如下：

输入： 观测矩阵Φ、观测向量y和步长s

初始化：

r0=y(初始化残余)

F0=[](初始化支撑集)

I=s(初始阶段支撑集的大小)

k=1(迭代次数)

j=1(初始化段下标)

重复执行：

Sk=Max(|Φ*rk-1|,I)(预选集)

Ck=Fk-1∪Sk(候选集)

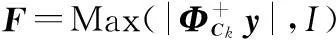
if满足停止条件

then退出此次迭代

else if ‖r‖2≥‖rk-1‖2(更新支撑集大小)

j=j+1 (更新段标)

I=j×s(更新支撑集的大小)

else

Fk=F(更新支撑集)

rk=r(更新残余)

k=k+1

end

end

重复以上步骤直到满足停止条件

其中,I=|Fk|是支撑集Fk的大小;对于矩阵a,函数Max(a,I)返回a中绝对值最大的前I个下标构成的下标集。对于集合Λ∈{1,…,N},ΦΛ是矩阵Φ中位于下标集Λ中的子矩阵。在第k次迭代中,Sk,Ck,Fk,rk分别代表预选集,候选集,最终支撑集和观测余量。

2.2MAMP算法

2.2.1初步估计稀疏度

SAMP算法根据步长信息逐步扩充支撑集,而步长s的选择是一个重构精度与重构速度难以同时满足的难题：如果选得较小,逐步增大支撑集大小会消耗大量的运算时间;如果选得较大,则无法准确逼近真实稀疏度,使得信号重构精度降低。

针对以上问题,MAMP利用文献[15]中提出的稀疏度估计过量判据。

2.2.2迭代停止条件的优化

SAMP算法中,在每一阶段,当搜索的支撑集原子更匹配原信号时,残余范数‖rk‖2减小,同时更新支撑集及残余。在不满足停止条件情况下,当残余范数增大时,进行段变换,同时增大支撑集的大小。如此,便增大了对停止条件‖r‖2≤opt×‖y‖2的依赖：对opt的选择,如果较大,则影响重构精度;反之则会一直增大支撑集的大小。当支撑集的大小增加到远大于真实稀疏度时,则会向支撑集引入大量错误原子,反而又降低了重构精度。因此,选择合适的停止条件显得尤为重要。

对于SAMP算法中opt的选择,往往是固定的,如通常假定opt=0.001以期得到更优的重建效果,但是,由于原始信号及稀疏矩阵的不同,往往将支撑集扩充到接近观测值也不能满足‖r‖2≤opt×‖y‖2,反而引入了更多的错误原子,因此,也就达不到自适应得到稀疏度的目的。

MAMP算法中,先对稀疏度进行初步估计,得到稀疏度的较小逼近,此时的稀疏度已经比较接近真实稀疏度,搜索到的支撑集也比较接近真实支撑集。在此基础上,继续搜索支撑集时,如果新的支撑集更准确,会降低‖r‖2;当‖r‖2后一次与前一次相等时,则说明对于当前支撑集的大小,已经搜索到了相对最优的支撑集,因此增大支撑集的大小,进一步降低‖r‖2;而当‖r‖2后一次大于前一次时,则说明在当前支撑集的大小不变时,已经引入了错误原子,则认为此时得到的支撑集便是最优支撑集,退出循环。前一阶段初步得到稀疏度的较小估计,后一阶段则逐一增加支撑集大小,精确逼近稀疏度,并得到相对最优的支撑集,解决了由于opt的选择不当,使支撑集被扩充至远大于真实稀疏度的问题。

2.2.3MAMP算法流程

以下是MAMP算法的具体流程：

输入： 观测矩阵Φ、观测向量y、测量值个数M

初始化：

I=M(初始化支撑集大小)

r0=y(初始化残余)

F0=[](初始化支撑集)

k=1(迭代次数)

重复执行：

步骤 1

I=I/2(初步估计稀疏度)

Sk=Max(|Φ*rk-1|,I)(预选集)

Ck=Fk-1∪Sk(候选集)

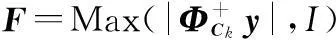
步骤 2

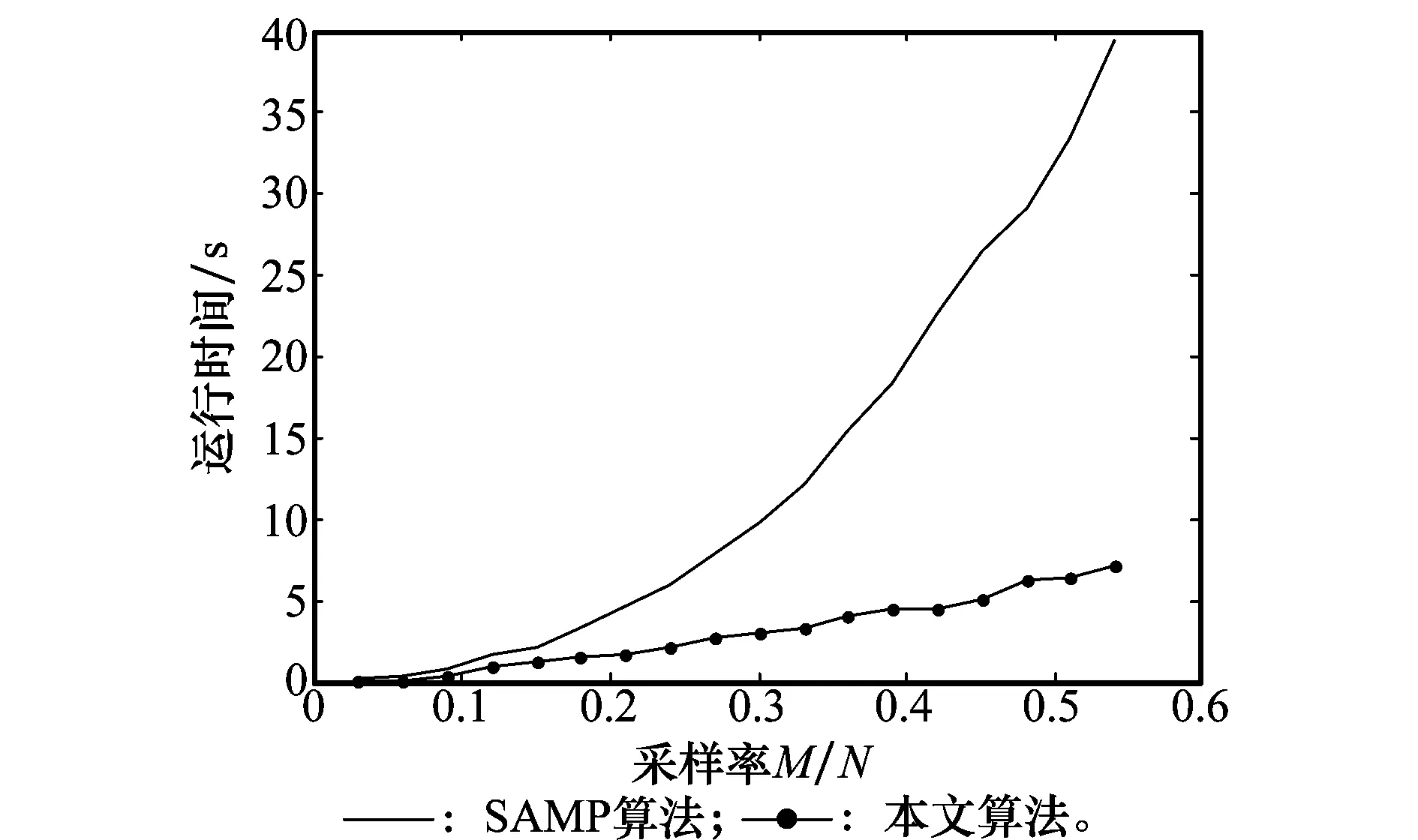
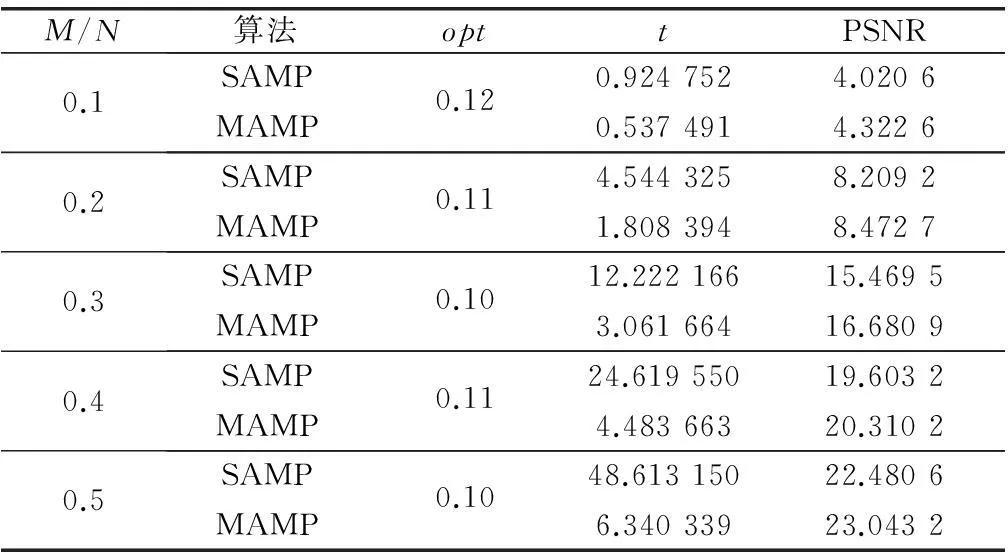
当停止条件(‖r‖2

Sk=Max(|Φ*rk-1|,I)(预选集)

Ck=Fk-1∪Sk(候选集)

if ‖r‖2>‖rk-1‖2

退出循环;

else if ‖r‖2=‖rk-1‖2

I=I+1(增加支撑集大小)

else

Fk=F(更新支撑集)

rk=r(更新残余)

k=k+1

end

end

重复以上步骤直到停止条件成立

步骤1初步完成了对稀疏度的过小估计,步骤2中,根据残余范数‖r‖2的变化情况来决定是否退出循环、或增大支撑集大小、或继续更新支撑集。

对于迭代停止条件的优化,避免了由于opt选择的不当,盲目地扩充支撑集的大小。MAMP算法中,没有完全依赖停止参数opt的选择,而是根据具体信号自适应地得到最优支撑集,从而大大提高了重构精度。同时,第一阶段的快速逼近稀疏度,也为真实稀疏度的寻找节省了大量时间。

3实验结果及分析

为比较本文算法与SAMP算法,实验采用Lena.bmp和Mondrian.bmp灰度位图(像素256×256)。实验程序是在3.19GHz、3.47GB内存、采用WindowsXP系统的计算机上运行,在MATLABR2010b环境下进行操作的。

实验中,均以列为单位进行处理,采用离散小波变换作为正交基,生成M×N维的随机矩阵作为测量矩阵,其中,M为观测矩阵y的维数,N为原始信号x的维数,M/N称为压缩比,压缩比越小,则重构过程中使用的观测数目越少。

实验的性能指标分别采用运算时间、峰值信噪比(peak signal to noise ratio, PSNR)和重构误差err。其中,运行时间为逐列采用重构算法直至整幅图像重构完成所需的时间,由tic oc函数完成;PSNR和重构误差err由以下2式给出：

PSNR是评鉴画质所广泛使用的客观量测法,衡量处理后的影像品质;重构误差是重构后图像与原始图像差值同原始图像之间的比值,同样是衡量图像处理的一个重要指标。PSNR越高,err越小,重构质量越好。

在SAMP中,当参数opt变化时,取采样率为0.3,0.4, 0.5,对Lena图进行重构,得到的PSNR与MAMP重构的图像的PSNR的比较如图1所示。

从图中可以看出,并不是停止条件参数opt选得越小,得到的重构图像就越精确,其最优值的选取,依不同问题而定。从本次实验可以看出,当opt选得较小时,重构效果较差;对于Lena图,当opt选在0.10～0.15区域内时,可达到相对最优的重建效果;而当大于该最优值时,重建PSNR会大幅降低。同时,实验中又附加了MAMP算法在相应采样率下的重构PSNR,解决了对opt的最优选取问题,同时,PSNR明显高于SAMP算法。

算法运行时间则随采样率的增大而增加, 图2展示了对于Lena图,在不同采样率下,分别利用SAMP和MAMP算法进行重构所需的运行时间的比较,可看出,MAMP算法在运行时间方面明显优于SAMP。

图1　SAMP算法和MAMP算法的PSNR比较

图2　SAMP和MAMP算法的运行时间比较

表1则记录了对于Mondrian图在不同采样率下,当SAMP取得最优重建PSNR时的时间t和PSNR与MAMP算法重建所需时间t和PSNR的比较。

表1　SAMP和MAMP算法对Mondrian图重建的t和PSNR比较

对于Mondrian图,当采样率增大时,重建所需时间增加,PSNR也提高,但是MAMP算法运行时间明显小于SAMP,且重建效果也有所提高。

当固定采样率,如取M/N=0.4时,利用SAMP和MAMP算法,采用相同的正交基和测量矩阵,分别进行压缩及重构,重建效果如图3所示。

图3　SAMP和MAMP算法对Lena和Mondrian图的重构比较

取采样率M/N=0.4,对Lena图进行重构,以相对误差err作为重构精度的参考,各个算法的重构精度如表2所示。

表2　不同算法对Lena图的重构精度(相对误差)

SAMP算法由于自适应求得真实稀疏度,步长s和停止条件参数opt无法准确得到最优值,因此相对误差较大于其他算法。而MAMP算法在重构精度上则是最优的,进一步验证了MAMP算法优于SAMP算法,是一种较好的重建算法。

4结论

本文算法对SAMP算法中的稀疏度的初步估计和迭代停止的条件优化2方面进行了讨论。在初步估计稀疏度时,先对半减小,后逐一增加,前一阶段大幅提高了搜索速度;后一阶段则保证了重构精度。对于迭代停止时的条件,不再单纯依赖停止条件中参数opt的选择,而是根据当前所选支撑集的具体情况来确定是否增加支撑集大小、或搜索更精确支撑集、或停止搜索,完成了支撑集的自适应搜索及停止。实验表明,该算法相比SAMP有更快的收敛速度,并且重建效果更优。因此,本文算法是一种较好的自适应匹配追踪重构算法。

参考文献：

[1] Donoho D L. Compressed sensing[J].IEEETrans.onInformationTheory, 2006, 52(4):1289-1306.

[2] Kutyniok G. Theory and applications of com-pressed sensing[J].GAMM-Mitteilungen, 2013, 36(1):79-101.

[3] Qaisar S, Bilal R M, Iqbal W, et al. Compres-sive sensing:from theory to applications, a survey[J].JournalofCommunicationsandNetworks, 2013, 15(5):443-456.

[4] Kutyniok G.Compressedsensing:theoryandapplications[M]. New York:Cambridge Uni-versity Press, 2012.

[5] Jiao L C, Yang S Y, Liu F, et al. Development and prospect of compressive sensing[J].Chi-neseJournalofElectronics, 2011, 39(7):1651-1662.(焦李成,杨淑媛,刘芳,等.压缩感知回顾与展望[J]. 电子学报,2011,39(7):1651-1662.)

[6] Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal match-ing pursuit[J].IEEETrans.onInformationTheory, 2007, 53(12):4655-4666.

[7] Donoho D L, Tsaig Y, Drori I, et al. Sparse s-olution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J].IEEETrans.onInformationTheory, 2012, 58(2):1094-1121.

[8] Zhao Q, Wang J K, Han Y H, et al. Compres-sive sensing of block-sparse signals recov-ery based on sparsity adaptive regularized orthogonal matching pursuit algorithm[C]∥Proc.oftheIEEEfifthInternationalConferenceonAdvancedComputationalIntelligence,2012:1141-1144.

[9] Dai W, Milenkovic O. Subspace pursuit for compressive sensing signal reconstruction[J].IEEETrans.onInformationTheory, 2009, 55(5):2230-2249.

[10] Needell D and Tropp J A. CoSaMP:Iterative signal recovery from incomplete and inaccu-rate samples[J].AppliedandComputationalHarmonicAnalysis, 2009, 26(3):301-321.

[11] Li J, Shen Y, Wang Q. Stepwise suboptimal iterative hard thresholding algorithm for compressive Sensing[C]∥Proc.oftheInstrumentationandMeasurementTechnologyConference, 2012:1332-1336.

[12] Do T T, Gan L, Nguyen N, et al. Sparsity ad-aptive matching pursuit algorithm for practi-cal compressed sensing[C]∥Proc.ofthe42ndAsilmatConferenceonSignals,Systems,andComputers, 2008.

[13] Chen S S, Donoho D L, Saunders M A. Atomic decomposition by basis pursuit[J].SLAMJournalonScientificComputing, 2006, 20(1):33-61.

[14] Gan W, Xu L P, Luo N. Adaptive recovery algorithm for compressive sensing[J].SystemsEngineeringandElectronics, 2011,33 (9):1948-1953.(甘伟,许录平,罗楠.一种自适应压缩感知重构算法[J]. 系统工程与电子技术, 2011, 33(9):1948-1953.)

[15] Tian W B, Fu Z, Rui G S. Blind adaptive ma-tching pursuit algorithm for signal reconstru-ction based on sparsity trial and error[J].Journalonommunications, 2013,34 (4):180-186. (田文飚,付争,芮国胜.基于分治试探的盲自适应匹配追踪重构算法[J].通信学报,2013, 34(4):180-186.)

吕伟杰(1975-),女,副教授,博士,主要研究方向为网络控制系统、小波网络、多模型控制理论、嵌入式系统、现场总线、压缩感知。

E-mail:weijielv@tju.edu.cn

E-mail:chenxiaqufu@163.com

刘红珍(1988-),女,硕士研究生,主要研究方向为压缩感知及图像处理。

E-mail:liuhongzhen_lhzh@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20141120.1831.002.html

Modified adaptive matching pursuit algorithm based on compressive sensing

LÜ Wei-jie, CHEN Xia, LIU Hong-zhen

(SchoolofElectricalandAutomation,TianjinUniversity,Tianjin300072,China)

Abstract:To improve the operating efficiency of sparsity adaptive matching pursuit (SAMP), a modified adaptive matching pursuit algorithm (MAMP) is presented. The new algorithm estimates the value of sparsity preliminarily in the process of the choice of the support list, meanwhile, it corrects the condition when the circulation stops. The experiments demonstrate that the new algorithm saves much more operating time than SAMP, and improves the performance of the recovery.

Keywords:compressive sensing(CS); adaptive; matching pursuit

通讯作者陈霞(1989-),,女,硕士研究生,主要研究方向为压缩感知的重建算法。

作者简介：

中图分类号：TN 911.72

文献标志码：ADOI:10.3969/j.issn.1001-506X.2015.05.35

收稿日期：2014-04-19；修回日期：2014-10-18；网络优先出版日期：2014-11-20。