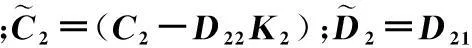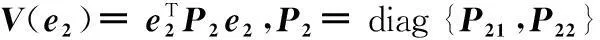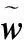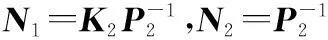双星载旋转机构非确定等价鲁棒自适应控制

许　晨, 陆宇平, 姚克明,2, 刘燕斌

(1. 南京航空航天大学航天学院, 江苏 南京 210016;

2. 江苏理工大学电气信息工程学院, 江苏 常州 213001)



双星载旋转机构非确定等价鲁棒自适应控制

许晨1, 陆宇平1, 姚克明1,2, 刘燕斌1

(1. 南京航空航天大学航天学院, 江苏 南京 210016;

2. 江苏理工大学电气信息工程学院, 江苏 常州 213001)

摘要：针对航天器携带的两副旋转机构同时姿态机动的精确控制问题提出一种鲁棒自适应控制方法。从关联系统的角度建立系统动力学模型,有效精确描述系统内各刚体动力学耦合项与非耦合项。采用“航天器本体姿态稳定、同时各旋转机构姿态机动”的复合控制策略:考虑到航天器本体转动惯量参数无法精确获得,应用非确定等价自适应控制方法设计姿态稳定控制器,在确保姿态全局渐近稳定的同时有效令不确定参数估计值精确逼近真实值或进入特定集合;考虑到各旋转机构姿态机动时受到航天器本体动力学耦合的影响,设计了鲁棒H∞姿态机动控制器以抑制动力学耦合的作用。仿真结果验证了所提出方法的有效性。

关键词：双旋转机构航天器; 关联系统; 非确定等价自适应控制; H∞控制

0引言

由于应用需求航天器往往携带各类旋转机构。如中继卫星安装大型中继天线、气象卫星装备微波辐射计和微波散射计等。为提高利用效率通常期望航天器允许多副旋转机构同时工作。如美国跟踪与数据中继卫星[1]的两副星载旋转天线可以同时进行目标跟踪或数据中继。然而各旋转机构姿态机动时与航天器本体存在敏锐的动力学耦合,这增加了各旋转机构进行姿态精确控制的难度。

由于较高的工程应用价值,此类携有旋转机构的多刚体航天器姿态精确控制问题引起了国内外学者广泛关注。文献[2]采用鲁棒增益调节控制方法对携带两副旋转机构的航天器设计鲁棒姿态控制器。文献[3]建立了携带一副二自由度观测器的空间观测卫星姿态动力学模型,并应用滑模控制方法针对航天器本体设计了喷气式bang-bang控制器。文献[4]针对携单幅大型旋转天线的中继卫星姿态控制问题利用一类解耦装置进行解耦控制。文献[5]将自抗扰控制方法应用于航天器本体姿态稳定及太阳帆板对日定向的复合控制器设计。文献[6]分析比较了重力场下地面物理仿真与真空环境下多体航天器动力学特性的不同点,具有实际意义。文献[7-8]研究了航天器本体与旋转附件同时进行姿态机动的复合控制问题。然而上述文献多数仅考虑了携带单幅旋转机构的情形,此外都没有考虑系统参数不确定性的问题。

由于燃料消耗或液体晃动等原因,航天器的转动惯量参数存在难以实时精确获得的情况。自适应控制可以有效解决参数不确定性的问题因此被广泛应用[9-12]。但上述文献都应用到确定性等价原理[13],即将系统不确定参数的实时估算值作为真实值以进行控制器设计,但对估算值的精确性问题并没有考虑。文献[14]首次提出非确定等价自适应方法,在解决参数不确定性问题时有效考虑到参数估计值的精确性问题。文献[15]将其应用于机械臂的姿态控制,文献[16]针对气动弹性系统采用了上述控制方法。基于此,本文应用非确定等价自适应方法为航天器本体设计姿态稳定控制器,在确保航天器本体姿态稳定性的同时有效令转动惯量参数的估计值精确逼近真实值或进入特定集合。

航天器携带的各旋转机构姿态机动时受到航天器本体带来的动力学耦合影响。其本质可以看作关联系统,即具有多个相互作用、相互关联子系统的系统[17]。文献[18-19]应用H∞控制方法针对关联系统设计了鲁棒控制器并取得良好效果。基于此,本文为星载的两副旋转机构姿态机动设计鲁棒H∞控制器,以抑制航天器本体动力学耦合带来的影响。

1双旋转机构航天器动力学模型

本文首先从关联系统的角度建立双旋转机构航天器姿态动力学模型,有效精确描述系统内各刚体动力学耦合项与非耦合项,为进行姿态精确控制做准备。

如图1所示,为描述双旋转机构航天器系统内各刚体的运动,建立坐标系如下:

惯性坐标系OXYZ:原点O位于地球中心,OX轴指向春分点,OZ轴指向北极,OY轴由右手定律给出。

轨道坐标系oxyz:原点o位于系统质心,ox，oy，oz轴与OX、OY、OZ坐标轴平行。

航天器及各旋转机构本体坐标系Oixiyizi(i=1,2,3):原点Oi位系统于各运动体质心,Oixi，Oiyi，Oizi三轴固定于各运动体的惯量主轴。

考虑旋转机构B2绕其本体坐标系O2x2y2z2的O2x2轴方向作一自由度旋转运动,转轴经过B2的质心;旋转机构B3绕其本体坐标系O3x3y3z3的O3y3轴方向作一自由度旋转运动,转轴经过B3的质心。采用牛顿欧拉动力学建模方法建立系统姿态动力学模型,过程如下。

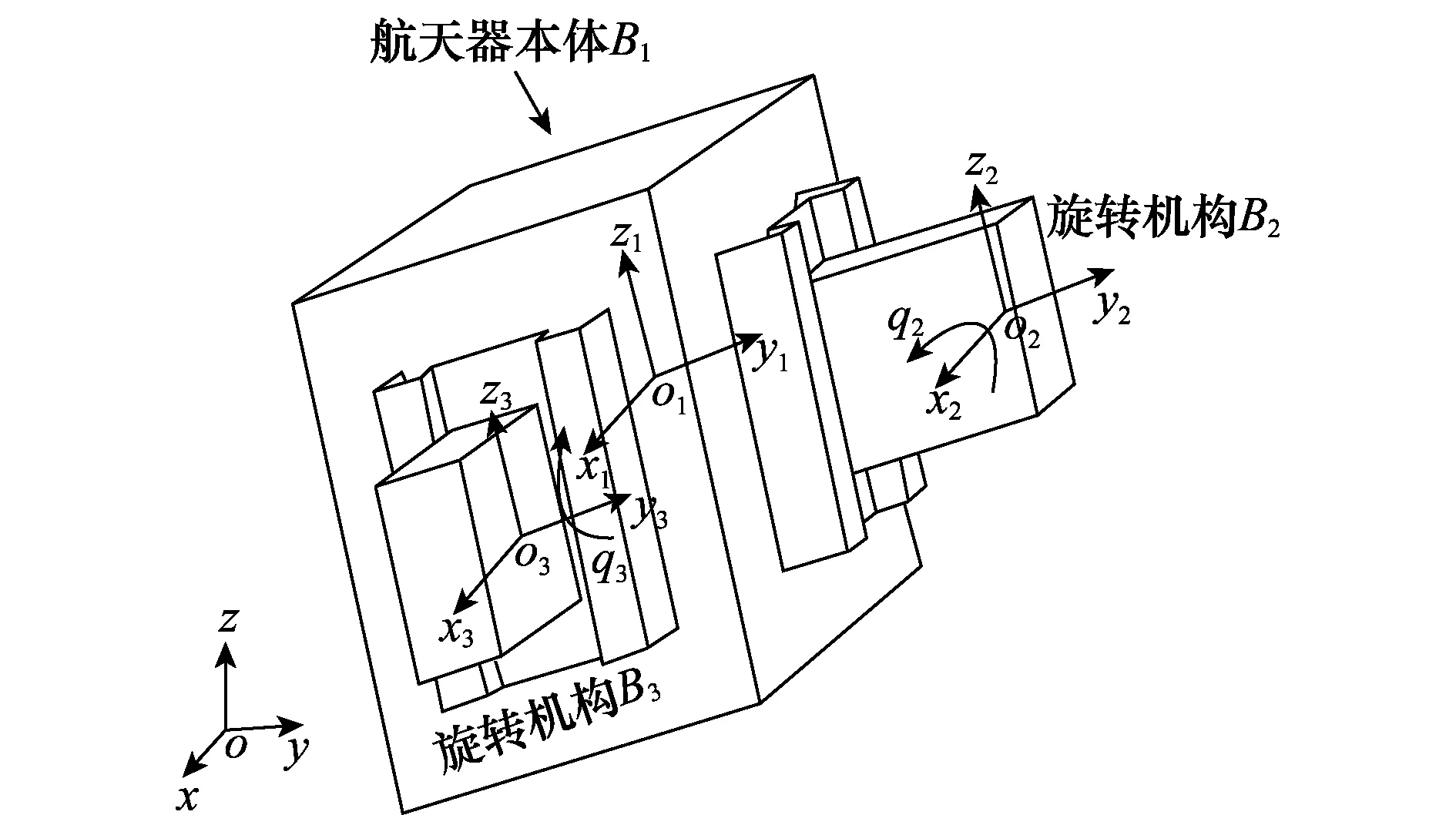
图1　双旋转机构航天器示意图

1.1航天器本体动力学模型

对于航天器本体B1,在本体坐标系O1x1y1z1中建立姿态运动学模型。为便于计算忽略系统轨道角速度ω0(考虑到ω0≪ω1的情况)的影响,得

(1)

忽略铰接触力的影响,在本体坐标系O1x1y1z1中建立B1姿态动力学模型

(2)

式中,J1=diag{J1x,J1y,J1z}为B1的主轴惯量阵; ω1∈R3×1表示惯性角速度矢量;T1∈R3×1表示B1受到的主控力矩。Ti∈R3×1(i=2,3)表示旋转机构B2与B3受到的力矩,在各自的本体坐标系Oixiyizi(i=2,3)中定义,A1i(i=2,3)表示坐标系Oixiyizi(i=2,3)相对于O1x1y1z1的方向余弦阵。定义q2、q3分别为B2与B3相对B1转过的角度,易得

式(1)和式(2)共同描述了航天器本体B1的姿态运动。

选取状态量x11= q1,x12= ω1,x1=[x11,x12]T,控制量u1=T1,测量输出y1=x1,根据式(1)和式(2)建立航天器本体B1的状态空间方程

(3)

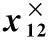
1.2旋转机构动力学模型

对于旋转机构B2,在本体坐标系O2x2y2z2中建立姿态运动学方程。惯性角速度ω2表达式为

(4)

式中,ω1表示航天器本体B1的惯性角速度矢量;A21表示坐标系O1x1y1z1相对于O2x2y2z2的方向余弦阵,易得

ω12表示B2相对B1的转动角速度,易得

(5)

由式(4)和式(5)得

(6)

由于B2绕其本体坐标系O2x2y2z2的O2x2轴作旋转运动,作为控制器设计角度考虑仅需建立该自由度的姿态运动学方程,即

(7)

在本体坐标系O2x2y2z2中建立B2姿态动力学方程

(8)

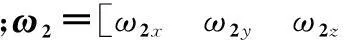
(9)

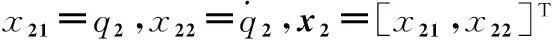
(10)

式中,F2代表动力学耦合项,有效描述航天器本体对B2带来的运动耦合。其余各项为非耦合项。

对于旋转机构B3过程同B2,在本体坐标系O3x3y3z3建立姿态运动学方程

(11)

式中,ω1表示航天器本体B1的惯性角速度矢量;A31表示坐标系O1x1y1z1相对于O3x3y3z3的方向余弦阵;ω13表示B3相对B1的转动角速度。同理仅需考虑B3单自由度的运动学方程,即

(12)

在本体坐标系O3x3y3z3建立姿态动力学方程

(13)

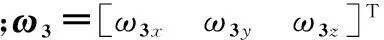
(14)

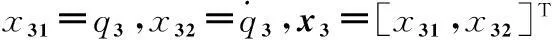
(15)

式中,F3代表动力学耦合项矩阵,有效描述航天器本体运动对B3带来的运动耦合。其余各项为非耦合项。

2鲁棒自适应姿态控制器设计

针对航天器携带的两副旋转机构同时进行姿态机动精确控制问题,本文采用“航天器本体进行姿态稳定、同时各旋转机构进行姿态机动”的复合控制策略。控制器设计过程如下。

2.1航天器本体非确定等价自适应控制器

对于航天器本体B1的状态空间方程式(3),姿态稳定控制器设计目标为在转动惯量参数J1存在不确定性的条件下使得当t→∞时状态量x1→0。

首先定义变量[15-16]如下:

(16)

(17)

式中,设定的参数常量α1>0,变量x12∈R3×1为航天器本体B1的角速度,xm2∈R3×1, Wm∈R3×3。变量W∈R3×3定义如下

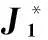
以便推导,经计算得

(18)

考虑自适应控制律如下:

(19)

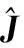
(20)

式中,设定的参数常量α4>0。T2y,T2z与T3x,T3z可分别由式(6)、式(8)及式(11)和式(13)联立获得,T2x与T3y可由旋转机构的控制律获得。由此可得定理1。

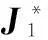
(21)

令

(22)

代入式(21),得

(23)

即

(24)

推得

(25)

式中,Cm2为常数向量;Cm2·e-a1t为指数衰减项数值趋于零,故将其省略[13,15]得

(26)

(27)

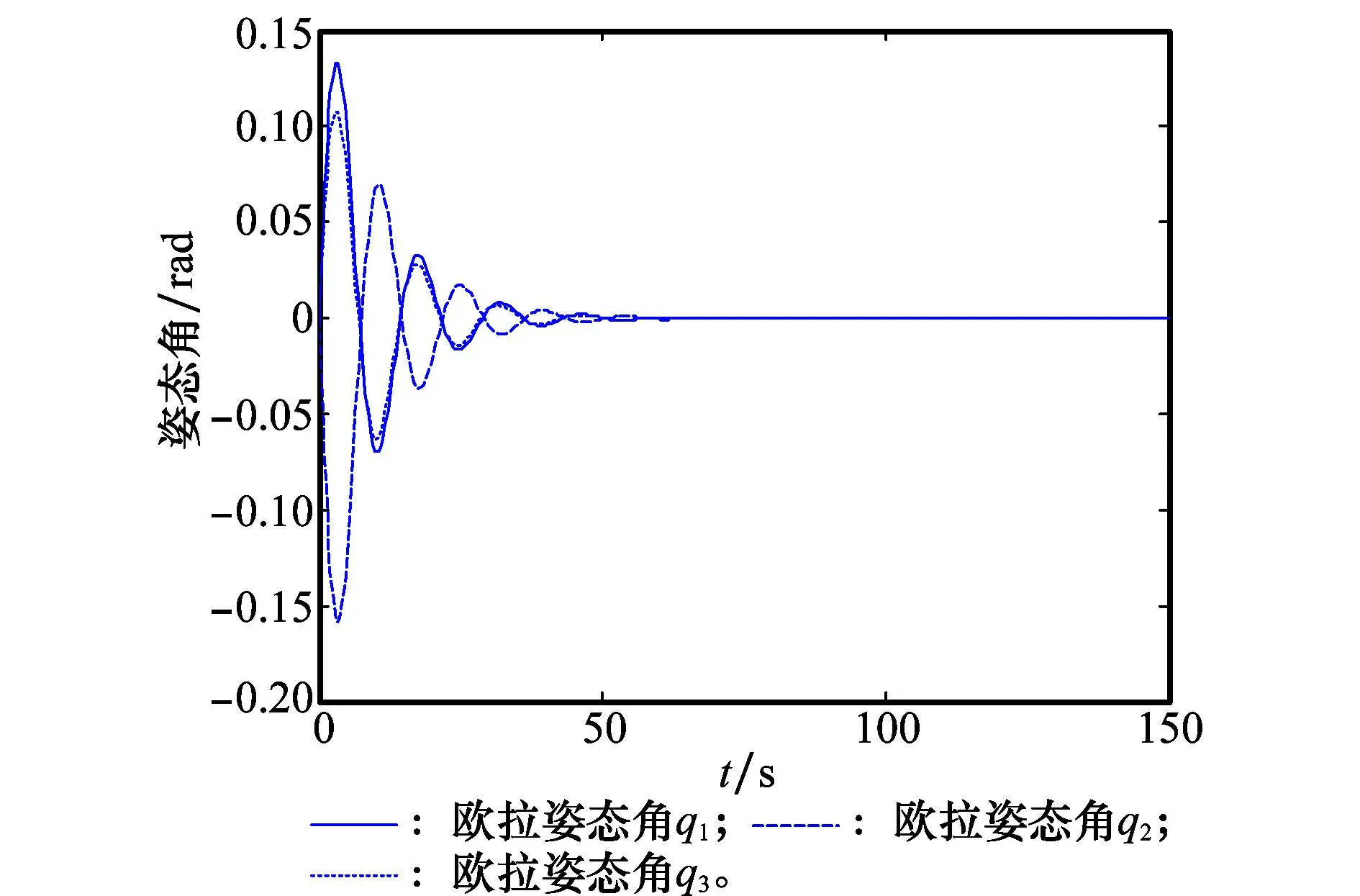
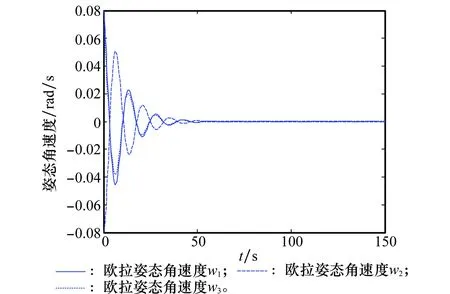
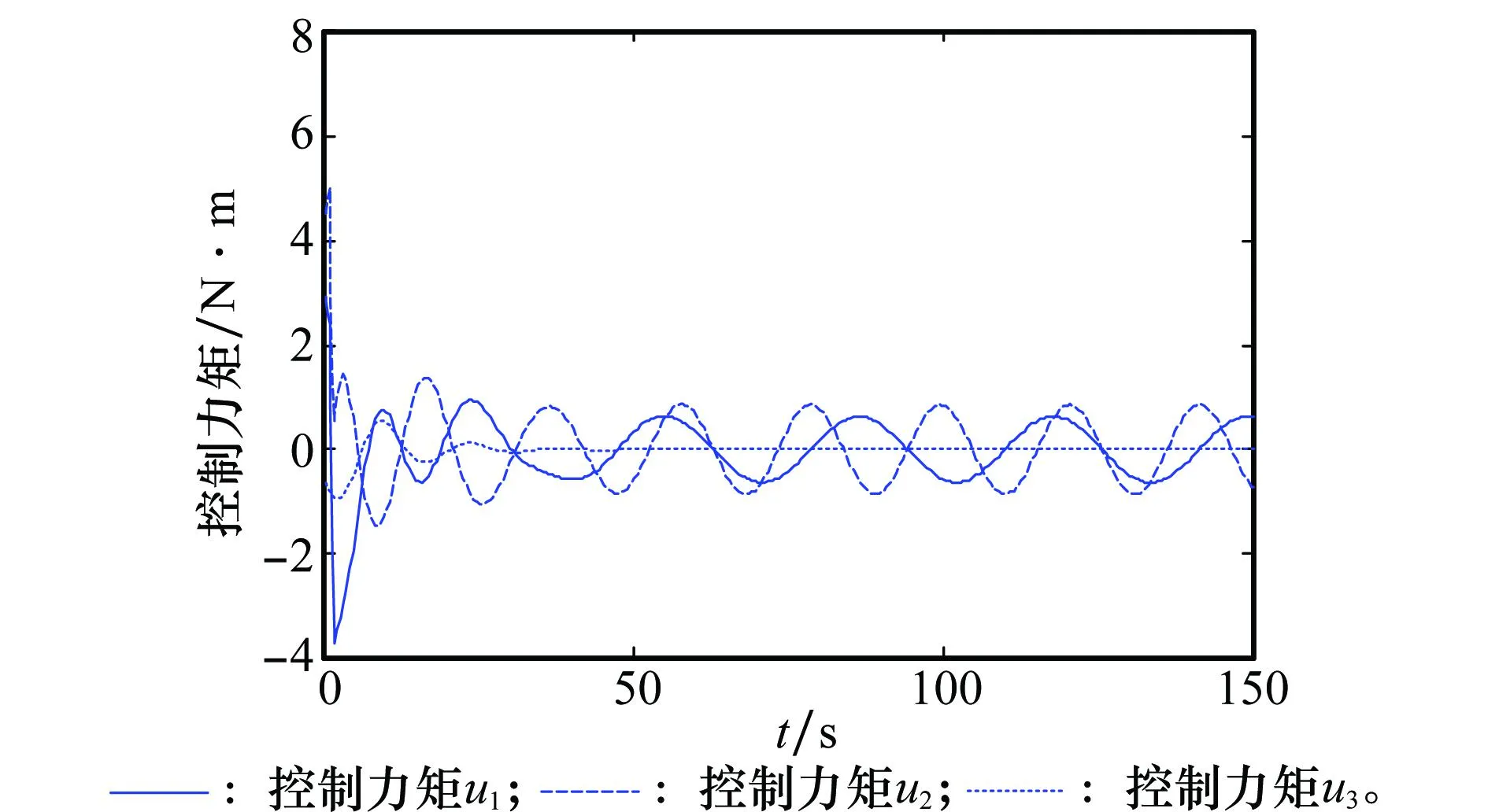
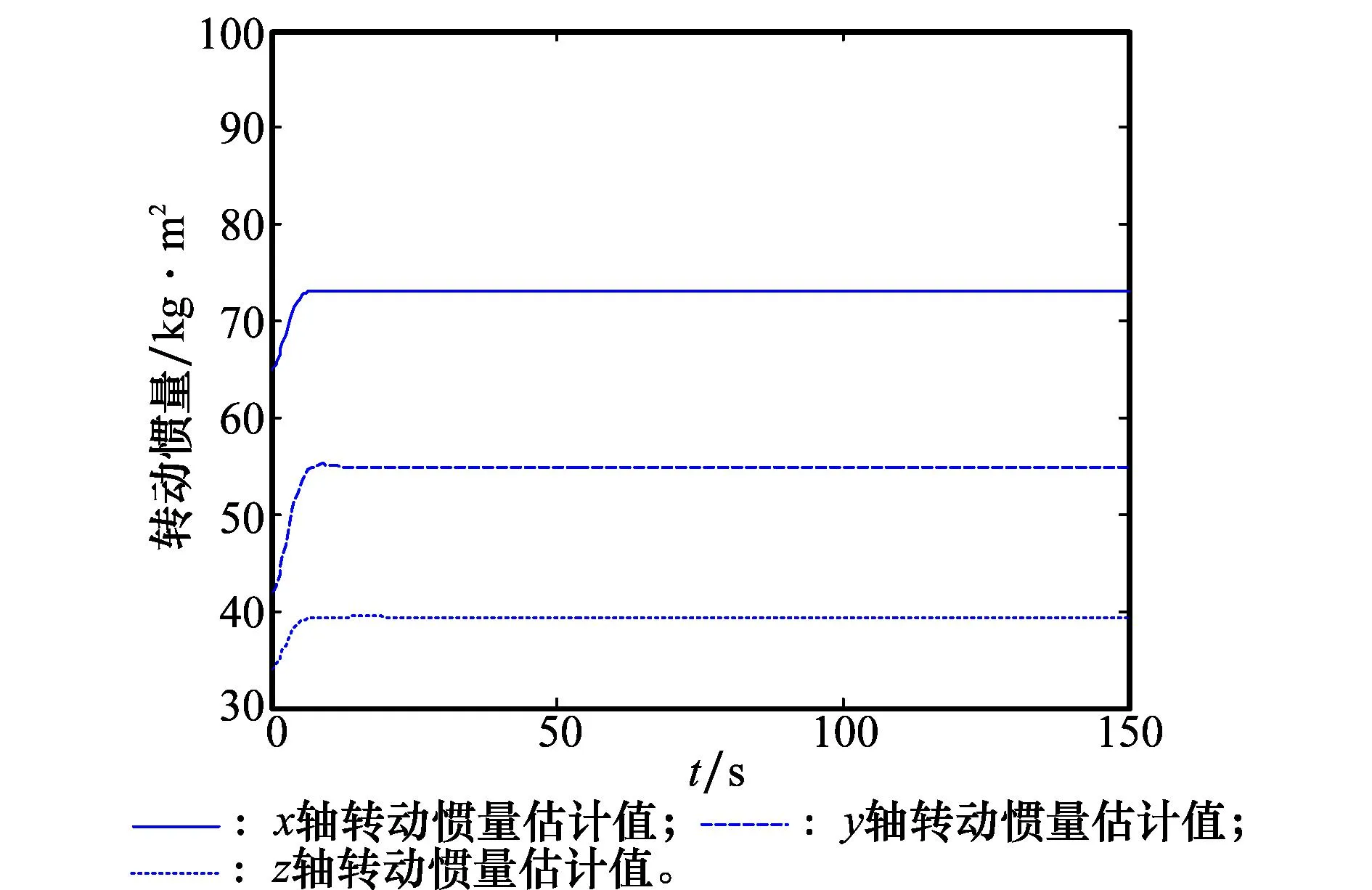
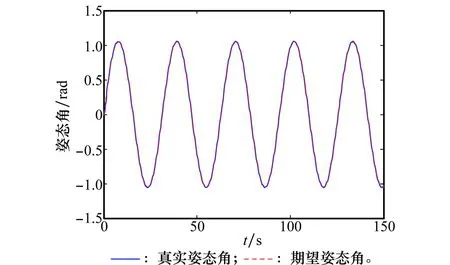
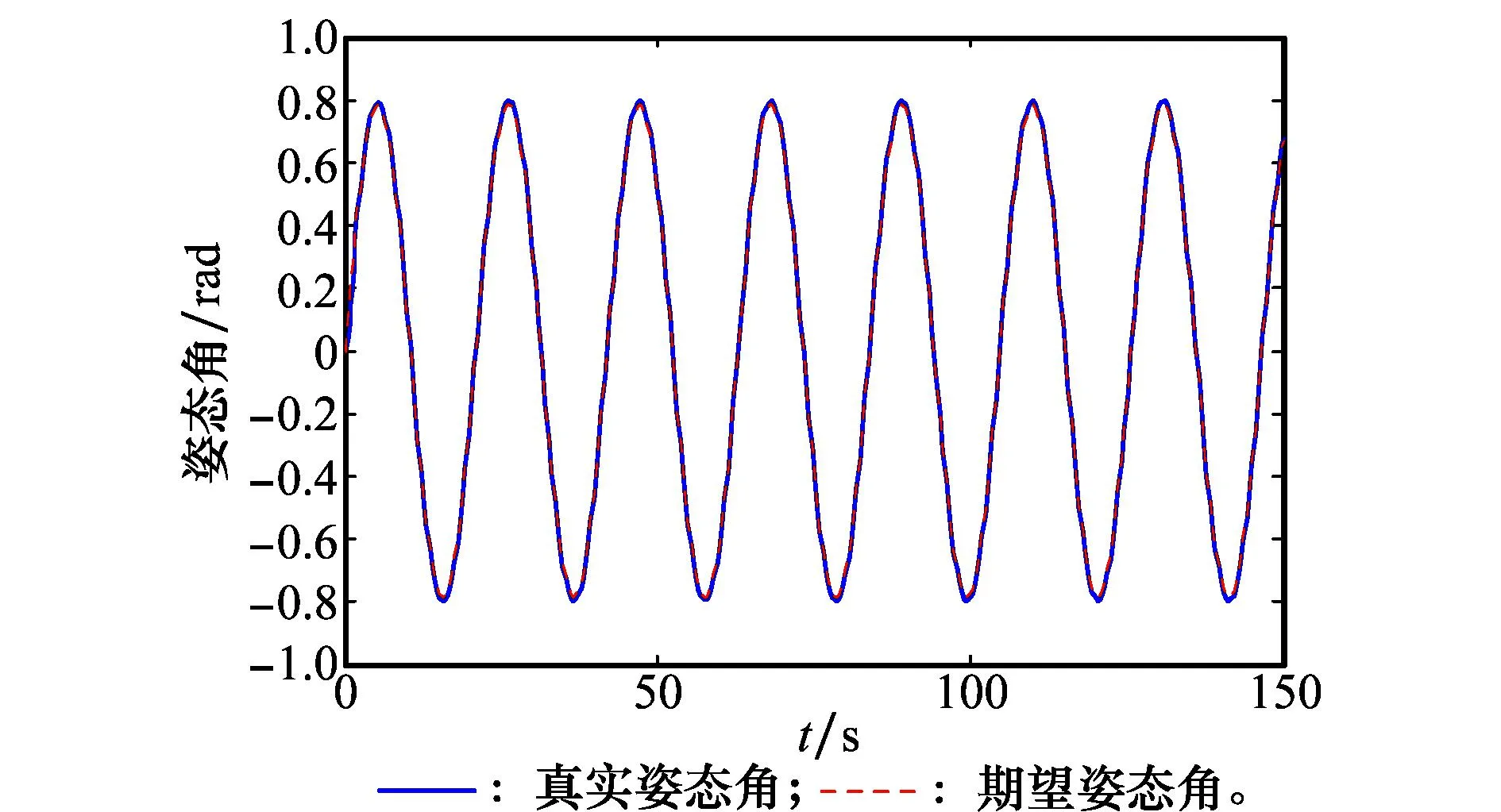
选取b1>max[1/(α2·α4),1/(α3·α4)],0

(28)

对式(27)两边求导,将式(3)、式(16)、式(26)和式(27)代入并考虑到α1=α2+α3,得

(29)

证毕

2.2旋转机构鲁棒H∞控制器

对于旋转机构B2与B3,姿态机动控制器设计目标为控制各旋转机构姿态精确跟踪目标指令,以执行侦察探测等任务。本文为各旋转机构姿态机动设计鲁棒H∞控制器,以抑制航天器本体动力学耦合带来的影响。

针对旋转机构B2,考虑期望目标指令x2r变化规律为

(30)

控制律设计如下:

(31)

式中,K2=[K21K22]∈R1×2表示控制反馈系数;e2=x2-x2r表示跟踪误差。由式(10)、式(30)和式(31)得

(32)

令z2∈R2×1表示式(10)的评价输出[19],表达式为

(33)

(34)

由式(34)得,若

(35)

则

由Schur补性质,式(35)等价为

(36)

由此可得定理2。

考虑到式(36)中未知变量K2和P2以非线性形式出现不易求解,因此令不等式(36)分别左乘和右乘矩阵diag{P-12,I,I},得

<0

(37)

3仿真研究

图2　本体欧拉姿态角

从仿真结果可以得出,在航天器转动惯量参数未知的情形下,通过本文设计的非确定等价自适应控制器航天器本体姿态最终保持稳定。由图2和图3可得航天器姿态在经过约60 s后趋于稳定,收敛速度较快。由图4知航天器本体控制力矩呈周期性变化,以抵消旋转机构的动力学耦合影响。从图5可得航天器转动惯量参数估计值最终精确逼近真实值。对于控制参数α1～α4的选取,参数α2,α3主要影响控制力矩的幅值,增大α2和α3可以缩短航天器姿态稳定的时间,但需要以增大控制力矩为代价。参数a1与a4主要影响不确定参数估计值的变化速率与最终取值,决定其最终逼近真实值或进入特定集合。

图3　本体欧拉姿态角速度

图4　本体控制力矩

图5　本体转动惯量估计值

旋转机构B2及B3各参数如下。

转动惯量矩阵:

J2=diag{1599}kg ·m2

J3=diag{171211}kg ·m2

姿态角和角速度的初始值均为零

目标姿态角:

计算得到的控制器参数:

K2=[97.875 474.192 8]

K3=[72.965 857.623 4]

对各旋转机构姿态机动进行控制仿真实验,仿真结果如图6和图7所示。

图6　旋转机构B2姿态角

图7　旋转机构B3姿态角

图6描述了旋转机构B2的姿态角变化曲线,图7给出了B3的姿态角变化曲线。由仿真结果可得通过设计的鲁棒H∞控制器,航天器本体带来的动力学耦合得到有效抑制,各旋转机构姿态精确跟踪跟踪目标指令,精度较高。

4结论

本文针对航天器携带的两副旋转机构同时进行姿态机动的精确控制问题设计了鲁棒自适应复合控制器。首先通过牛顿欧拉方法建立系统姿态动力学模型,精确获得各刚体的动力学耦合项与非耦合项。之后运用非确定等价自适应方法为航天器本体设计了姿态稳定自适应控制器,有效解决传统自适应方法参数估计值精确性的问题,进一步提高了控制性能。借鉴关联系统控制相关方法为各旋转机构设计了鲁棒H∞姿态机动控制器,有效抑制航天器本体动力学耦合带来的影响。仿真结果表明,通过合理选择控制器参数本文设计的两种控制方法达到预期目标,为工程设计提供一定参考价值。

参考文献：

[1]ToralM,StocklinF,Bar-serverY,etal.Extremelyaccurateon-orbitpositionaccuracyusingNASA’strackinganddatarelaysatellitesystem(TDRSS)[C]∥Proc.of the 24th AIAA International Communications Satellite Systems Conference,2006:1-9.

[2]NagashioT,KidaT.Robustcontrolofspacecraftwithmobileappendages[J]. Transactions of the Japan Society for Aeronautical and Space Sciences, 2001, 44(143):40-47.

[3]JingWX,XiaXW,GaoCS,etal.Attitudecontrolforspacecraftwithswinginglarge-scalepayload[J]. Chinese Journal of Aeronautics, 2011,24(3):309-317.

[4]GeSM,WangL,GanKL,etal.Amethodfordecouplingcontrolofsatellite-bornelargespaceantenna[J]. Journal of Astronautics, 2013,34(1):46-53.(葛升民,王磊,甘克力,等.星载大型空间天线的一种解耦控制方法[J]. 宇航学报,2013,34(1):46-53.)

[5]SiZH,LiuYW.Highaccuracyandhighstabilityattitudecontrolofasatellitewitharotatingsolararray[J]. Journal of Astronautics, 2010,31(12):2697-2703.(斯祝华,刘一武.帆板驱动影响下的卫星姿态高精度高稳定度控制[J]. 宇航学报,2010,31(12):2697-2703.)

[6]ZhouJ,ChenHL,LiuYY,etal.Investigationonconsistencybetweenmulti-bodysatelliteandgroundphysicalsimulationsystem[J].Journal of Astronautics, 2010,31(2):355-360.(周军, 陈欢龙, 刘莹莹, 等.多体卫星地面物理仿真的抑制性研究[J].宇航学报,2010,31(2):355-360.)

[7]LiF,LeiYJ.Terminalslidingmodecompoundcontrolmethodformulti-bodyspacecraftattitudemaneuver[J]. Aerospace Control and Application,2014,40(1):31-36.(黎飞,雷拥军. 多体航天器姿态机动的终端滑模复合控制方法研究[J].空间控制技术与应用,2014,40(1):31-36.)

[8]GouXY,ChenYQ,LiTS,etal.Introductiontosimultaneousmaneuversandcompositecontrolofspacecraftplatformanditsappendages[J]. Aerospace Control and Application,2009,35(5):1-5.(苟兴宇,陈义庆,李铁寿,等.平台与附件同时机动及其复合控制初探[J]．空间控制技术与应用,2009,35(5):1-5.)

[9]MaGF,ZhangHB,HuQL.Backstepping-basedrelative-attitudecontrolfortheleader-followerspacecrafts[J].Control Theory & Applications, 2012,29(6):797-802.(马广富,张海博,胡庆雷.基于反步法的主从航天器相对姿态控制[J].控制理论与应用,2012,29(6):797-802.)

[10] Li B, Hu Q L, Shi Z, et al. Backstepping and dynamic control-allocation for attitude maneuver of spacecraft with redundant reaction fly-wheels[J].ControlTheory&Applications, 2012,29(11):1419-1425.(李波,胡庆雷,石忠,等.基于反步法与动态控制分配的航天器姿态机动控制[J].控制理论与应用,2012,29(11):1419-1425.)

[11] Zou A M, Kumar K D. Adaptive attitude control of spacecraft without velocity measurements using Chebyshev neural network[J].ActaAstronautia, 2010,66(5/6):769-779.

[12] Liu Y C, Zhang T, Song J Y, et al. Adaptive spacecraft attitude tracking controller design based on similar skew-symmetric structure[J].ChineseJournalofAeronautics,2010,23(2):227-234.

[13] Krstic K, Kanellakopuolos I, Kokotovc P.Nonlinearandadaptivecontroldesign[M]. New York:Wiley,1995.

[14] Ortega R, Hsu L, Astolfi A. Immersion and invariance adaptive control of linear multivariable systems[J].SystemsandControlLetters,2003, 49(1):37-47.

[15] Seo D, Akella M R. Non-certainty equivalent adaptive control for robot manipulator systems[J].SystemsandControlLetters, 2009, 58(4):304-308.

[16] Lee K W, Singh S N. Non-certainty-equivalent adaptive control of a nonlinear aeroelastic system[J].InternationalJournalofElectronicsandTelecommunications, 2010,56(4):463-471.

[17] Song B. Robust stabilization of decentralized dynamic surface control for a class of interconnected nonlinear systems[J].InternationalJournalofControl,AutomationandSystems,2007,5(2):138-146.

[18] Labibi B, Marques H J, Chen T W. Decentralized robust output feedback control for control affine nonlinear interconnected systems[J].JournalofProcessControl,2009,19(5):865-878.

[19] Dhbaibi S, Tlili A S, Elloumi S, et al.H-infinity decentralized observation and control of nonlinear interconnected systems[J].InstrumentSocietyofAmericaTransactions,2009,48(4):458-467.

许晨(1986-),男,博士研究生,主要研究方向为多体航天器姿态精确控制。

E-mail:xuchen@nuaa.edu.cn

陆宇平(1957-),男,教授,博士研究生导师,主要研究方向为多运动体协调控制,高超声速飞行器控制。

E-mail:yplac@nuaa.edu.cn

姚克明(1978-),男,副教授,博士,主要研究方向为图像匹配与飞行控制。

E-mail:nuaa_yaokeming@163.com

刘燕斌(1980-),男,副教授,硕士研究生导师,主要研究方向为高超声速飞行器控制。

E-mail:liuyb@nuaa.edu.cn

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20141209.0959.009.html

Non-certainty equivalent robust adaptive control for

spacecraft with double rotary mechanisms

XU Chen1, LU Yu-ping1, YAO Ke-ming1,2, LIU Yan-bin1

(1.CollegeofAstronautics,NanjingUniversityofAeronauticsandAstronautics,

Nanjing210016,China;2.CollegeofElectricandInformationEngineering,

JiangsuUniversityofTechnology,Changzhou213001,China)

Abstract:A robust adaptive attitude control method is investigated for two rotary mechanisms attitude tracking accurately of spacecraft. A system dynamic model is established referring to the form of the interconnected system, in which the coupled part and uncoupled part of each rigid-body are described accurately. A control strategy that the main body of spacecraft controlled for attitude stabilization and each mechanism controlled for attitude tracking synchronously is adopted. Considering it is hard to obtain the inertia matrix of the main body of spacecraft accurately, a controller based on the non-certainty equivalent adaptive method is designed to make the attitude of the main body of spacecraft global asymptotic stabilized and the estimated parameters either reach to the true value or come to a particular set. Considering there exists acute dynamic coupling between the main body of spacecraft and mechanisms, a robust H∞ attitude maneuver controller is designed to alleviate disturbance due to dynamic coupling. Simulation results show the effectiveness of the proposed strategy.

Keywords:spacecraft with double rotary mechanisms; interconnected system; non-certainty equivalent adaptive control; H∞control

作者简介：

中图分类号：V 448.22

文献标志码：ADOI:10.3969/j.issn.1001-506X.2015.05.24

基金项目：国家自然科学基金(91016017)；江苏省自然科学基金(BK20130234)；江苏省普通高校研究生科研创新计划(CXZZ120160)资助课题

收稿日期：2014-07-21；修回日期：2014-10-24；网络优先出版日期：2014-12-09。