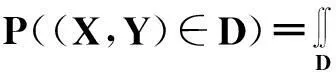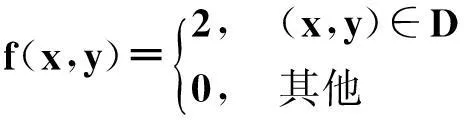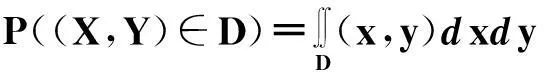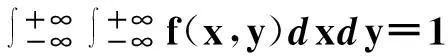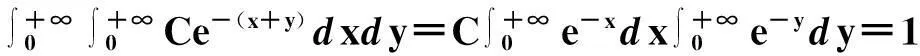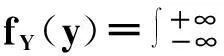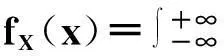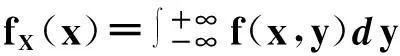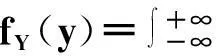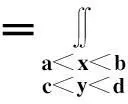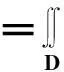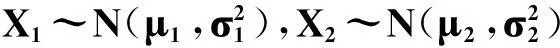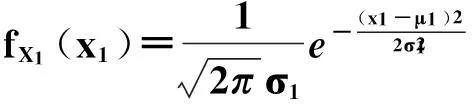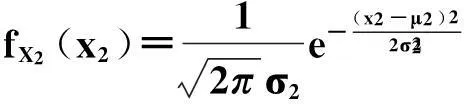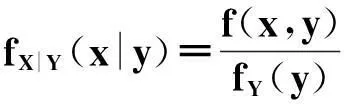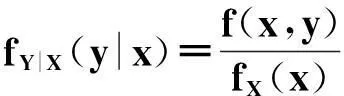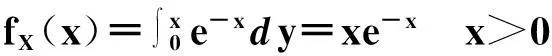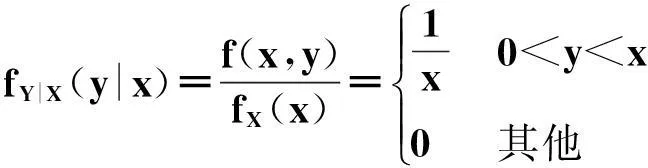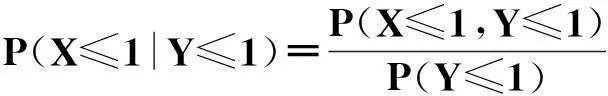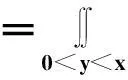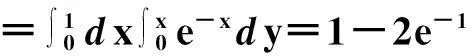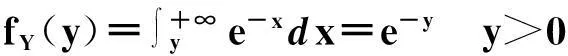有关二维连续型随机变量与分布的教学内容探讨
2015-02-17熊允发
熊允发, 管 涛
(中国人民公安大学网络安全保卫学院, 北京 100038)
有关二维连续型随机变量与分布的教学内容探讨
熊允发,管涛
(中国人民公安大学网络安全保卫学院, 北京100038)
摘要我们称n个随机变量X1,X2,…,Xspan的整体ξ=(X1,X2,…,Xspan)为n维随机变量或称随机向量。对于二维连续型随机变量与分布这一部分内容的讲解,主要应从概念的界定入手,着重讲解它的分布规律以及它们的相关关系,即:联合密度、边缘密度、联合密度与边缘密度的关系(积的关系、商的关系)。
关键词连续型; 随机向量; 分布
0引言
众所周知,概率统计是大学理工科学生的一门必修专业基础课,它概念新颖,应用广泛,涉及面宽,在实际应用中存在各种各样的问题,这样就给学生们的学习带来了很多的困难。作者根据二十多年的教学经验,又查阅了诸多国内外的相关书籍,就二维连续型随机变量与分布的教学内容简单地谈几点教学心得,希望能给广大教师和学生以新的启迪。
1连续型随机向量的概念界定
为了研究问题的方便,我们仅以二维连续型随机变量为例。
如果二维随机变量ξ=(X,Y)可能取的值不是只有有限个或者可列个(即可排成一个序列),则称ξ=(X,Y)为连续型的。若(X,Y)是连续型的,则X,Y都是一维连续型随机变量。反之,也成立。下面我们将其从数学意义上严格定义一下:
【定义】对于二维随机变量ξ=(X,Y),如果存在非负可积函数
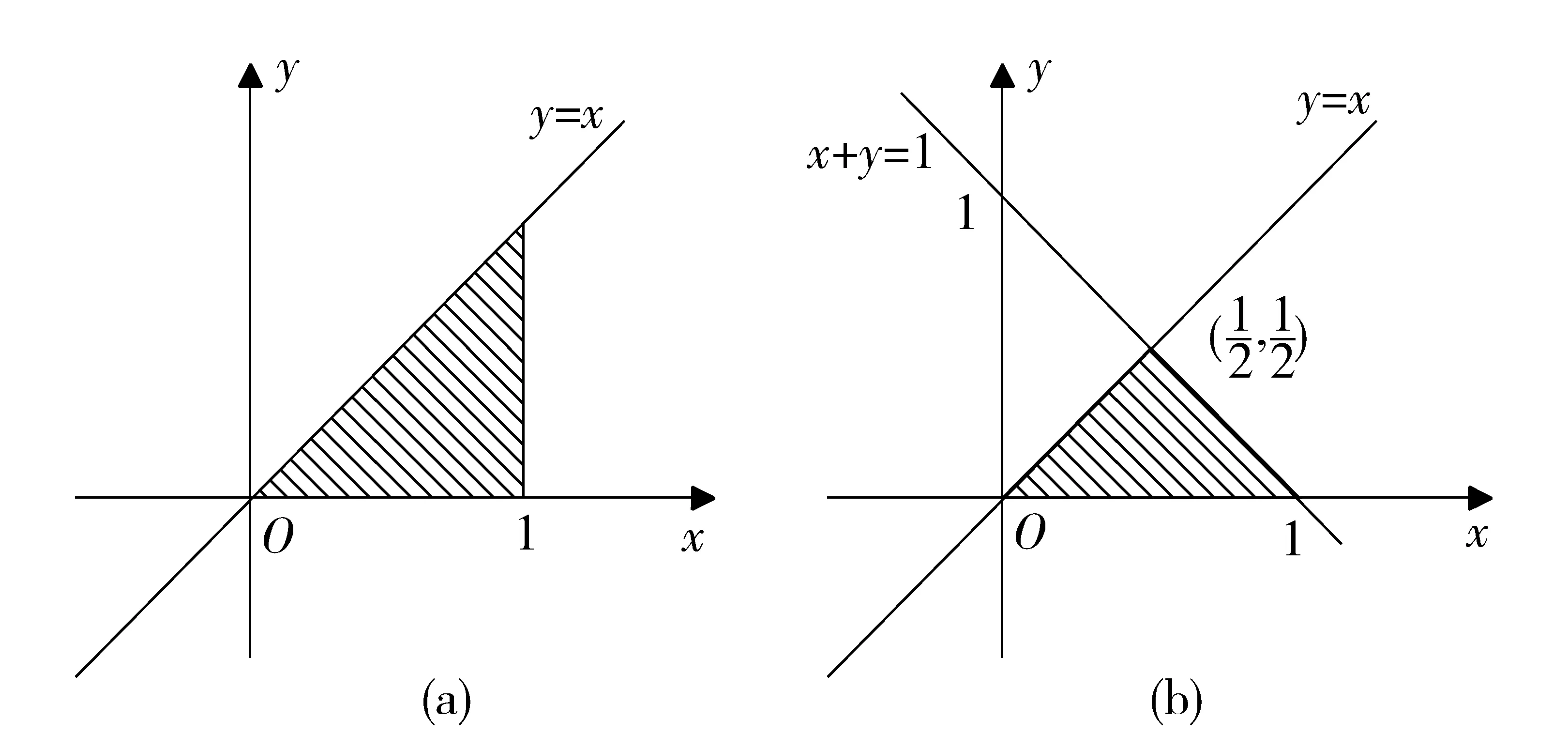
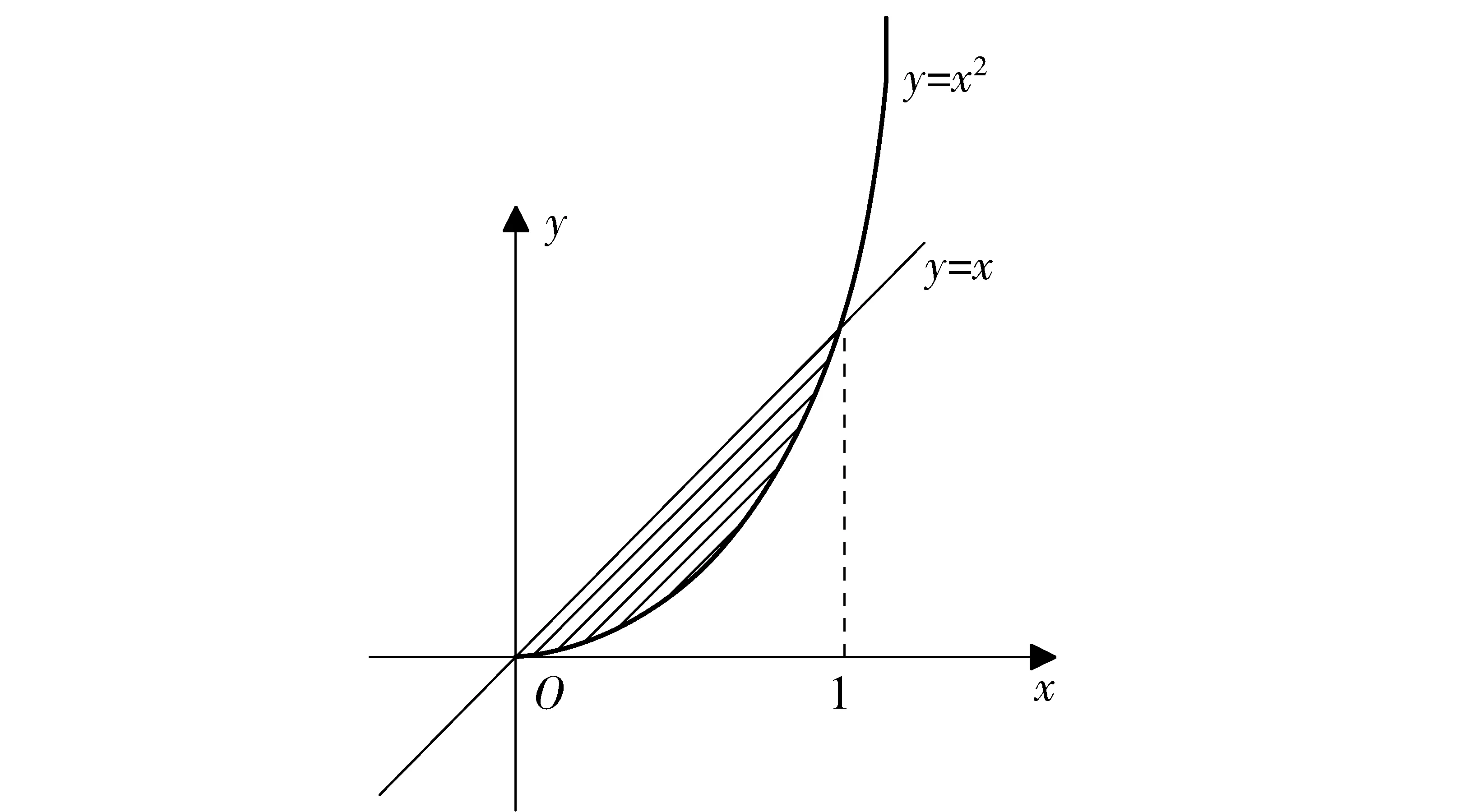
f(x,y)(-∞ 使对任意一个邻边分别平行于坐标轴的矩形区域D:“即由不等式a 则称二维随机变量ξ=(X,Y)为连续型的,并称f(x,y)(-∞ 【注释】该定义中的f(x,y)是非负可积的函数,积分区域D是平面上的任意区域[1]。 简言之,二维连续型随机变量落在平面上任意区域的概率就等于密度函数在该区域上的二重积分。 【例1】设(X,Y)服从D上的均匀分布, 求P(X+Y≤1)的值。 其中D:x≥y,0≤x≤1,y≥0.见图1(a)。 图1 解:D的面积S=1/2,所以(X,Y)的概率密度为 f(x,y)dxdy 见图1(b)所示。 2连续型随机向量的分布规律 所谓分布,就是随机向量取各个不同值的概率的集合。二维连续型随机变量(向量)的分布,指的就是以上定义中f(x,y)的不同积分的集合。为便于理解,我们分以下三个部分加以介绍。 1)联合密度 (1)定义:称以上定义中f(x,y)为ξ=(X,Y)的联合分布密度(简称联合密度)。 (2)性质:对于连续型随机变量ξ=(X,Y)可以证明,对于平面上任意的集合D,均有 这里f(x,y)是联合分布密度,且具有: ①非负性 f(x,y)≥0; ③若f(x,y)在(x,y)点连续,F(x,y)在(x,y)点处的二阶偏导数存在且连续,则有 (3)几何意义: 由(2)得,二维随机变量ξ=(X,Y)落在平面上任一区域D内的概率就等于联合密度f(x,y)在D上的积分,也就是把概率的计算转化为一个二重积分的计算。由此指出(X,Y)∈D的概率,数值上就等于以曲面z=f(x,y) 为顶,以平面区域D为底的曲顶柱体的体积,这就给出了f(x,y)的几何意义[2]。 【例2】设(X,Y)的联合密度为 求(1)常数C; (2)P(0 ∴C=1 (2)D=((x,y):0 ∴P(0 2)边缘分布密度 (1)定义:对于二维随机变量(X,Y)作为其分量的随机变量X(或Y)的密度函数fX(x)(或fY(y)),称为(X,Y)的关于X(或Y)的边缘分布密度。 (2)问题:已知联合密度f(x,y),如何求边缘分布密度fX(x),fY(y)? 若(X,Y)的联合密度是f(x,y),则X,Y的分布密度分别是 证明:由于{-∞ P(a 令D=((x,y):a P(a 根据随机变量分布密度的定义,不难看出 【注释】从以上的证明可以看出,联合密度决定了边缘密度。因此,我们做题分析问题时,一定要先求出联合密度[3]。 【定义】设G是平面上面积为a(0 则(X,Y)的联合密度为: 【例3】 设(X,Y)服从如图2所示区域G(抛物线y=x2和直线y=x所围成的区域)上的均匀分布,求联合分布密度和边缘分布密度。 图2 故所求(X,Y)的联合分布密度为 f(x,y)dy 3)联合分布与边缘分布的关系 (1)积的关系(联合密度等于边缘密度的乘积)具体的就是讲X与Y相互独立的问题。 何谓X与Y相互独立呢? 【定义】设X与Y是两个随机变量,如果对任意a 【定理】设X,Y分别有分布密度fX(x)和fY(y),则X与Y相互独立的充要条件是二元函数fX(x)·fY(y)为随机向量(X,Y)的联合密度。 即X,Y相互独立⟺f(x,y)=fX(x)·fY(y) 证明:①设fX(x)·fY(y)是(X,Y)的联合密度, P((a =P(a =P(a 可见,X与Y是相互独立的。 ②设X,Y相互独立, D=((x,y):a P((X,Y)∈D)=P(a =P(a 故fX(x)·fY(y)是(X,Y)的联合密度。 【注释】一般情况下,边缘密度是不能决定联合密度的。只有当X,Y相互独立时,两个边缘密度的乘积就是它们的联合密度。即当X,Y独立时,边缘密度也能确定联合密度[4]。 解:由题意 故(X1,X2)的联合密度为 f(x1,x2)=fX1(x1)·fX2(x2) (2)商的关系(条件分布密度等于联合密度除以边缘密度) 【注释】要求条件分布密度,首先要知道联合密度,其次要求出边缘密度,两者的比值即为条件概率密度[5]。 【例5】设二维随机变量(X,Y)的概率密度为 ①求条件概率密度fY|X(y|x) ②求条件概率P(X<1|Y<1) 其中 P(X≤1,Y≤1) 参考文献 [1]王展青,李寿贵. 概率统计[M].北京:科学出版社,2000:83-84. [2]钱小军. 数量方法[M].北京:高等教育出版社,1999:89-91. [3]李茂年,周兆麟.数理统计方法[M].天津:天津人民出版社,1982:58-70. [4]许承德. 概率统计[M].哈尔滨:哈尔滨工业大学出版社,2000:60-65. [5]李排昌,熊允发.概率统计[M].北京:中国人民公安大学出版社,2004:48-60. (责任编辑于瑞华) 作者简介熊允发(1963—), 男, 湖北仙桃人,教授。研究方向为概率统计与随机过程。 中图分类号D035.319