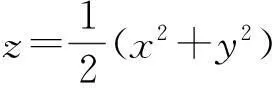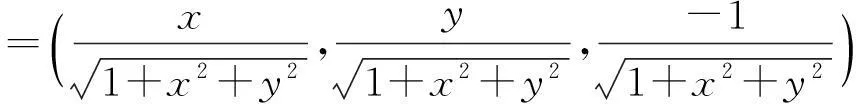光滑曲面的离散化研究

李排昌,　左　萍

(中国人民公安大学网络安全保卫学院， 北京　100038)



光滑曲面的离散化研究

李排昌,左萍

(中国人民公安大学网络安全保卫学院， 北京100038)

摘要在空间解析几何学中，点是构成曲面的基本单元，曲面是宏观意义下的几何图形，曲面的面积是宏观意义下的数学问题。宏观上一个曲面上的有理点是密集的，微观上该曲面上的有理点是离散的也是可数的[1]，用这种观点研究曲面积分问题，我们称之为离散化方法在曲面积分中的应用。作者通过经典实例对曲面积分的离散化方法进行论述和研究，揭示了曲面积分的奥秘，便于学生对相关内容的理解与掌握。

关键词曲面的对应有理散点图； 曲面面积； 曲面积分

0引言

积分是微积分学科中的难点和重点，曲面积分又是积分学中的难点和重点。本文正是针对这个主要问题展开研究的，我们采用连续变量的离散化方法推演曲面积分理论，揭示了曲面积分的奥秘。

设函数z=f(x,y)在X—型区域

D={(x,y)|a≤x≤b,φ1(x)≤y≤φ2(x)}

上连续。以区域D为底，以D的边界生成的柱面为侧面，以曲面

Σ∶z=f(x,y)

为顶形成曲顶柱体，我们已经知道有求此曲顶柱体体积V的二重积分公式[2](也称为二次积分公式)：

1曲面的面积(第一类曲面积分)

曲面面积的经典实例[3]：设二元函数

z=f(x,y)的定义域D是所谓的X—型：

D={(x,y)|a≤x≤b,φ1(x)≤y≤φ2(x)}

且函数z=f(x,y)在D上有连续的偏导数，函数z=f(x,y)在定义域D上的图形为曲面Σ，求曲面Σ的表面积S(第一类曲面积分)。

解：区域D内的每个有理点P(x,y)唯一对应曲面Σ上的一点M(x,y,f(x,y))。由于区域D内的有理点是密集的，D内的全体有理点为自变量所对应的函数图形在宏观意义下仍是连续曲面，在微观意义下是散点图(称为有理散点图或曲面的有理散点骨架，见图1)。区域D内有理点P以及与其相邻的3个有理点的坐标分别为

P(x,y)、P1(x+dx,y)、

P2(x,y+dy)、P3(x+dx,y+dy)

这4个点对应曲面上的4个点分别为

M(x,y,f(x,y))、M1(x+dx,y,f(x+dx,y))、

M2(x,y+dy,f(x,y+dy))、

M3(x+dx,y+dy,f(x+dx,y+dy))

忽略dx、dy的高阶的微元后

因此，可得

图1

图2

(1)

综上所述，第一类曲面积分问题实际是二重积分问题。

例1求球面x2+y2+z2=a2的表面积S(如图3)。

图3

D={(x,y)|x2+y2≤a2}

由于区域D内的有理点P(x,y)与曲面Σ上的有理散点M(x,y,f(x,y))存在一一对应关系，故求和范围可表示成区域D上的二重积分。所以，整个球面的表面积为

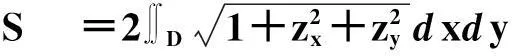
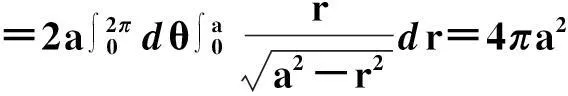
例2曲面Σ是球面x2+y2+z2=a2被平面z=b(0

求构件的质量m。

D={(x,y)|x2+y2≤a2-b2}

图4

由于

曲面Σ上有理散点M(x,y,z)处对应的占位质量为

由于区域D内的有理点P(x,y)与曲面Σ上的有理散点M(x,y,f(x,y))存在一一对应关系，故求和范围可表示成区域D上的二重积分。所以，整个构件的质量为

2 流向曲面一侧的流量(第二类曲面积分)

图5

流体流向曲面Σ指定侧的流量问题： 设稳定流动的不可压缩流体的速度场由

=(P(x,y,z),Q(x,y,z),R(x,y,z))

给出,Σ是速度场中的一片有向曲面，函数P(x,y,z)、Q(x,y,z)、R(x,y,z)都在Σ上连续, 求在单位时间内流向Σ指定侧的流体的流量Φ(也称为第二类曲面积分)。

而曲面Σ上有理散点M的占位面积为

(2)

如果曲面Σ的方程为y=g(x,z)，定义域为Dxz，函数y=g(x,z)在Dxz上有连续的偏导数；或者曲面Σ的方程为x=h(y,z)，定义域为Dyz，函数x=h(y,z)在Dyz上有连续的偏导数，同理有相应于(2)式的公式。

综上所述，第二类曲面积分问题实际是二重积分问题。

单位法向量为

曲面Σ上有理散点M的占位面积为

所以，把以上数据代入公式(2)得

∬Dxy[(z2+x)cosα-zcosγ]dS

=8π。

参考文献

[1]李排昌，王铁英．离散化方法在积分中的应用 [J] ．中国人民公安大学学报：自然科学版，2014，80(2)：93-96.

[2]吉林大学数学系．数学分析(中册)[M]．北京：人民教育出版社，1978：144-290.

[3]孙振绮．工科数学分析教程[M]．北京：机械工业出版社，2003：99-204.

[4]同济大学数学系．高等数学[M]．北京：高等教育出版社，2007：001-246.

(责任编辑于瑞华)

作者简介李排昌(1957—)， 男， 河北人， 教授。研究方向为基础数学。

中图分类号G642.0