含裂隙岩体单轴压缩裂纹扩展机制离散元分析
2015-02-17蒋明镜申志福
蒋明镜,张 宁,申志福,陈 贺
(1.同济大学 土木工程地下建筑与工程系,上海 200092;2.同济大学 土木工程防灾国家重点实验室,上海 200092;3.同济大学岩土及地下工程教育部重点实验室,上海 200092;4.云南省交通规划设计研究院 陆地交通气象灾害防治技术国家工程试验室,云南 昆明 650011)
1 引 言
自然界中的岩石经历了长期的地质构造作用,使坚硬的岩石材料含有大量的节理、裂隙等地质缺陷,致使岩石的强度降低且易发生脆性破裂。大量的岩土工程实践表明,工程的失稳破坏与裂纹缺陷的扩展和贯通有密切的关系[1]。为理清裂纹的扩展与贯通机制,很多学者以预制单条、双条以及多条裂隙岩石为研究对象,从室内试验、理论计算及数值模拟等方面开展了大量卓有成效的研究工作[2-10]:将单轴压缩破坏中的裂纹分为翼裂纹和次生裂纹;提出了双参数复合准则、拉应变断裂准则、最小J2准则和有效剪应力准则等压剪断裂理论。然而,理论分析很多情况下并不能合理地考虑岩石的各向异性、非均匀及不连续等特性;室内试验中成功预制裂隙具有较大的难度,而采用模型材料又不能完全模拟真实岩石的特性[11]。
而通过大量的细观试验研究,发现岩石破坏主要是裂纹沿着岩石晶体颗粒边界的扩展造成的[12]。而离散元正是一种从微观机制出发,利用非连续介质方法,在不需要较为复杂的本构关系的前提下,分析材料宏观破坏过程的数值计算方法。离散元模拟岩石破损的主要原理为将岩石抽象为岩石晶体颗粒与粒间胶结物所组成,建立适合的胶结接触模型反映岩石的在不同情况下的破坏过程。近年来,国内外已有许多学者采用离散单元法模拟岩石裂纹的扩展过程,分析了岩石的破裂机制,并通过与室内试验资料对比验证了该方法模拟岩石的可行性[13-14]。然而,通过蒋明镜等[13-14]的微观接触试验发现,胶结物质的破坏是法向、切向、转动向荷载共同作用的结果,而现阶段的离散元模型并不能完全考虑这些因素。
本文将基于室内微观胶结接触试验的岩石微观胶结模型嵌入离散元软件,对预制单裂隙的Lac du Bonnet 花岗岩石进行单轴压缩试验,对比分析压缩过程中试样中应力分布与理论计算的差异,并对裂纹扩展判据的适用性进行了对比研究。
2 离散元数值模拟
2.1 模型简介
由于岩石中胶结的存在,常规的离散元模型不能直接应用于岩石的模拟,基于有厚度水泥胶结颗粒的试验结果[15],通过理论分析推导出无厚度胶结颗粒的强度包线,采用C++语言与FISH 语言编写用户自定义的胶结接触模型,然后,通过离散元自带的模型添加接口即可将该模型嵌入。由于篇幅的限制,推导过程另文做详细介绍,此处只给出相应的结果。式(1)~(4)为室内试验总结得到的强度包线,图1为无厚度的胶结颗粒的强度包线。
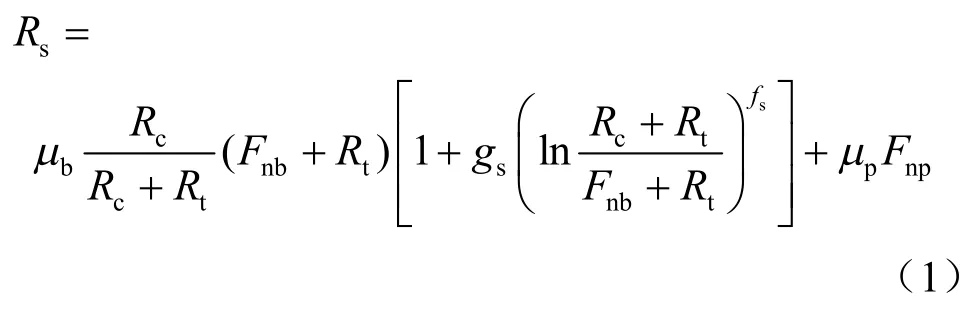
式中:Rs为峰值剪切荷载;μb为室内试验得到的参数;Rc、Rt分别为压缩强度和拉伸强度;Fnb、Fnp分别为作用在胶结和颗粒上的法向力;gs、fs分别为室内试验得到的参数;μp为颗粒的摩擦系数。
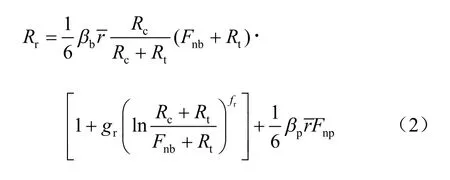
式中:Rr为峰值扭转荷载;βb为室内试验得到的参数;为两个胶结颗粒(半径分别为R1,R2)的平均半径,按计算;gr、fr分别为室内试验得到的参数;βp为颗粒抗转动系数。
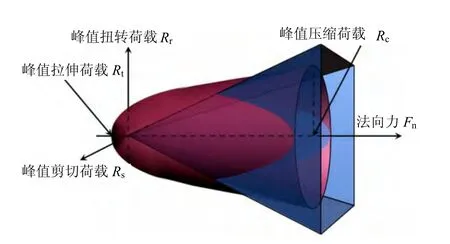
图1 胶结模型强度包面Fig.1 Strength envelop of bond model
胶结破坏后,胶结和颗粒会同时受力,定义此时为参与状态,则残余强度包线:
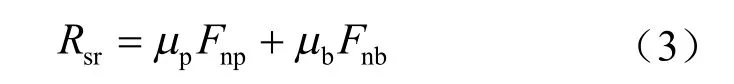
式中:Rsr为残余剪切荷载。
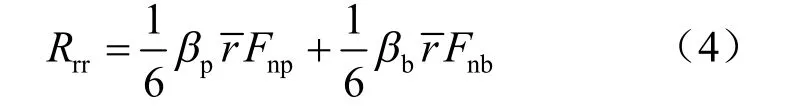
式中:Rrr为残余扭转荷载。
选用蒋明镜等[16-17]提出的考虑抗转动的胶结模型,其力学响应如图2 所示。图2(a)为胶结接触模型的法向力学响应。该力学响应中,法向力随着法向位移的增加而线性增加,当拉力达到胶结峰值拉伸荷载Rt时,胶结被拉坏,拉力突然跌落为0。图2(b)为胶结接触模型的切向力学响应。剪切力Fs随着切向位移us的增加首先线性增加,当达到峰值剪切荷载Rs时,胶结发生破坏,接触点的切向力突然跌落至恒定值,该恒定值由Mohr-Coulomb 准则计算得到。图2(c)为胶结接触模型的转动向力学响应。相对转角θ 同扭矩M 呈线性关系,达到峰值扭转荷载Rr之后,残余扭转荷载Rrr由颗粒材料形状和荷载类型进行确定。
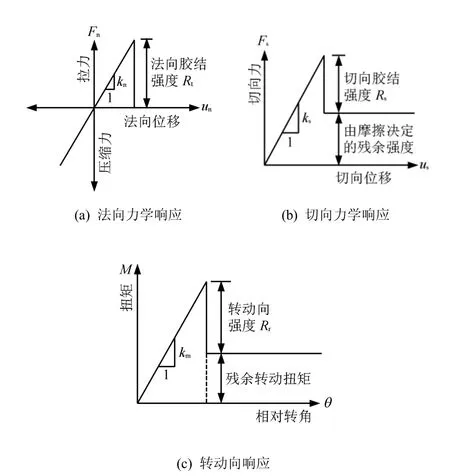
图2 无厚度胶结模型的力学响应[16-17]Fig.2 Mechanical responses of zero-thickness bond contact model
2.2 模型参数的选取
参照Lac du Bonnet 花岗岩特性[2],本文选择了如图3 所示的级配,用分层欠压法[18]制成平面孔隙比为0.2 的试样,然后保持一定的竖向压力为颗粒接触赋予接触模型成样。通过图4 所示的单轴压缩试验和巴西试验确定了试样的微观参数,如表1所示,试验得到试样的宏观参数为:单轴压缩强度为205 MPa,拉伸强度为11.36 MPa,泊松比为0.256。
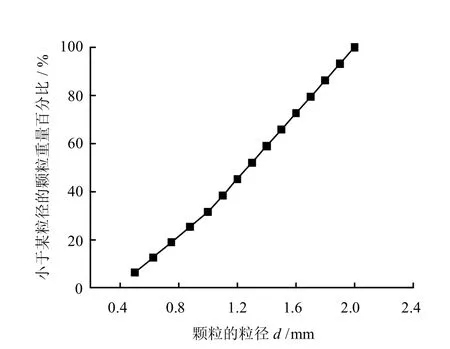
图3 DEM 岩石试样的级配曲线Fig.3 Particle size distribution of DEM rock sample
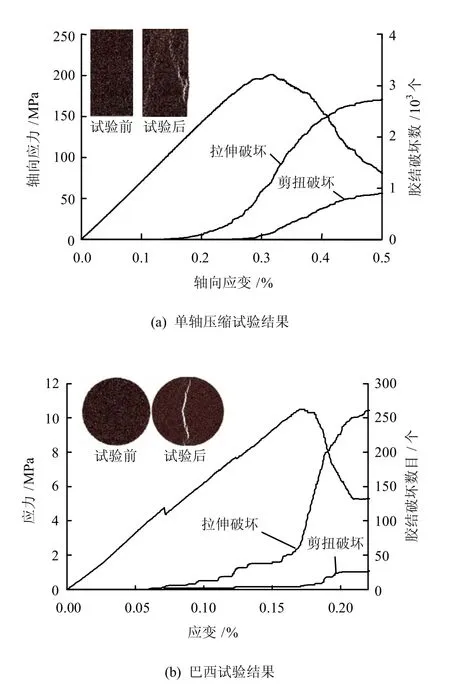
图4 DEM 试验结果Fig.4 Results of DEM simulation

表1 岩石胶结模型中的微观参数Table 1 DEM micro parameters of rock sample
2.3 预制裂隙的制样
预制裂隙代表此处物质的缺失,因此,先按照前节方法制成单轴试样备用,然后采用删除部分颗粒的方法进行预制裂隙,此时裂隙为张开状态。对于预制的单裂隙,裂隙中心与试样中心重合,为保持与室内试验相同的预制裂隙角度,选取与水平方向的角度α 分别为0°、30°、45°、60°、75°进行研究;预制裂纹形式和尺寸如图5 所示。在预制裂隙形成之后,循环至平衡,随后对岩石离散元试样进行单轴压缩试验。
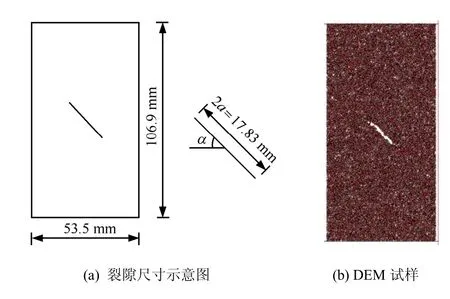
图5 预制裂隙试样Fig.5 Pre-cracked samples
3 试验结果分析
3.1 试验结果
表2为各倾角预制裂隙试样的破坏形态图与室内试验的对比,详细内容已另文介绍[19],本文只列出结果说明模型的合理性。

表2 DEM 模拟与室内试验[19]试样破坏形态对比Table 2 Comparison of failure modes between DEM and experimental results [19]
从表2 可以看到,DEM 模拟裂隙扩展形态与室内试验的相似度较高,都可以观察到明显的翼裂纹扩展:发启于裂纹端部向主应力方向发展。试验结果证明了模型模拟岩石的适用性,下文将从试样的应力分布和扩展判据来论述裂隙的扩展机制。
3.2 裂隙周围的应力分布
岩石中的裂隙是由岩石中应力引起胶结破坏导致的,预制裂隙的存在使岩石中应力的分布更加复杂和不均匀。因而,研究预制裂隙周围的应力分布对于揭示岩石裂隙的萌生和发育具有重要意义。
平面问题中的裂纹主要有两种类型:Ⅰ型(张开型裂纹)、Ⅱ型(滑开型裂纹)。Westergaard[20]提出了一个复变应力函数,通过假定给出了两种类型裂纹周围的应力场和位移。如图6 所示,中心有长为2a 的贯穿裂隙,边界作用拉应力σx和σy致使裂纹张开,即张开型裂纹(Ⅰ型);作用剪应力τ 使得裂纹相互剪切,即剪切型裂纹(Ⅱ型)。试样裂隙类型可视为两者的叠加。
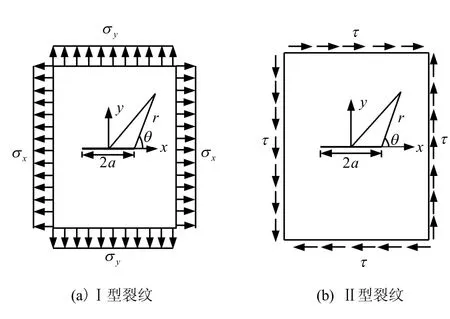
图6 裂纹类型Fig.6 Crack modes
根据其推导结论,在拉剪作用下裂纹周围的全场应力的表达式为
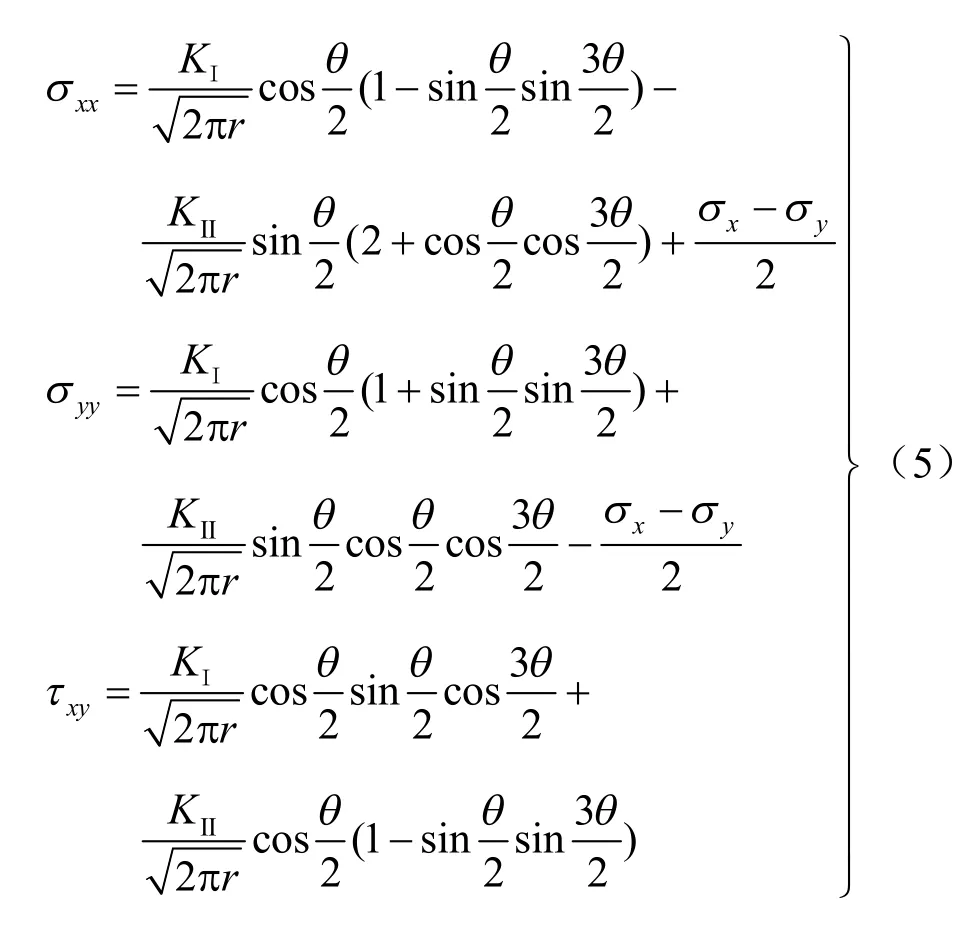
其中:KІ和KⅡ分别为Ⅰ型和Ⅱ型裂纹的应力强度因子;r 和θ为图6 中的几何参数。
对于如图7 所示的单轴压缩,试样承受着上下两侧的均布压力q,试样的中心位置为一张开型裂纹,该裂纹与加载方向的夹角为β,裂纹的长度为2a,设置笛卡尔坐标系(oxy)和极坐标系的原点分别在试样的中心和裂纹的右端点。据弹性力学坐标旋转公式可得oxy 坐标系下的等效边界应力
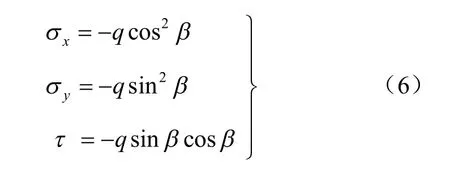
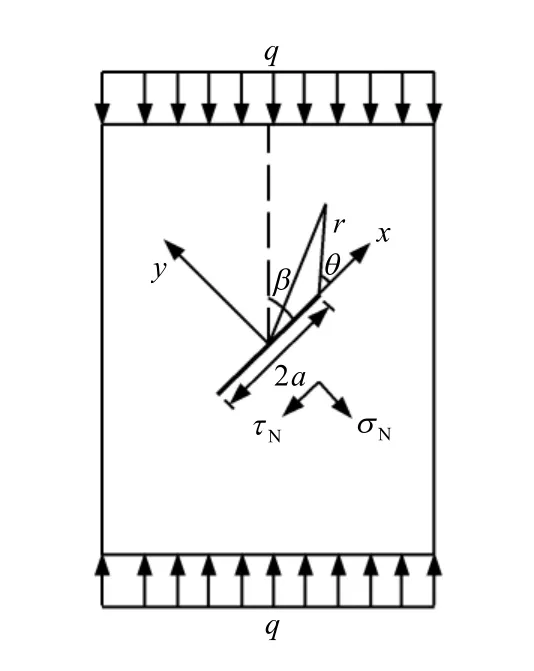
图7 裂纹扩展判据的计算模型Fig.7 Model for crack propagation criterion
将式(6)带入式(5)即得裂隙岩石单轴压缩的应力分布:

其中,应力强度因子为
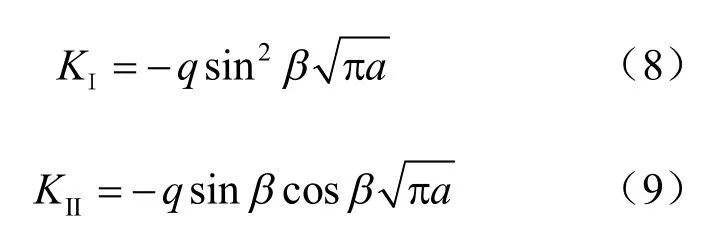
需要说明的是,在前文推导中裂纹受力为拉剪,若裂隙尚未闭合,则式(5)依然适用。在单轴压缩中裂纹周围为压剪受力。若裂纹在压剪受力时裂隙已经闭合,此时会有界面之间的摩擦力。在离散元模拟过程中,观察到在试样发生胶结破坏,即开裂之前,裂隙并未闭合,因此,式(5)依然适用。
表3为DEM 数值试验和理论分析得到的轴向应变0.7εp(εp为峰值应力对应应变)所对应的应力分布图。由表可以看出:(1)尽管由于各向同性的假设,预制裂隙试样中理论计算应力分布的数值与DEM 模拟得到的数值有差异,但当预制角度小于75°时,在定性规律上是一致的,在预制裂隙的周围出现了明显的应力集中现象,侧向应力σxx中拉应力集中于裂隙的上下两面、压应力集中于裂隙的左右两端,而切应力则在预制裂隙的上下两面和左右两端呈现相反的方向。产生这样现象的原因应该为轴向的压缩使裂隙有闭合的趋势,此时对于裂隙两端较大的压应变使裂隙上下两面产生拉应变,从而使裂隙周围产生拉应力。(2)而当预制裂隙角度为75°时,理论计算值中侧向应力σxx处于拉应力状态,而DEM 计算结果表明,此时试样处于拉压应力状态,但与轴向应力σyy相比数值较小,说明此时裂隙对试样整体的应力分布影响已经不大。(3)随着预制裂隙角度的增加,在达到0.7εp时,轴向应力会增加,而侧向应力的最大拉应力却越来越小,说明倾角较大的裂隙可以有效地减小应力的集中,也因此预制裂隙角度较大的试样具有更高的强度。
3.3 裂纹扩展判据
裂纹的扩展总是从应力集中的端部开始的,而从上节的分析中可知,裂隙的左右两端是压应力集中的地方,裂隙的上下两面是拉应力集中的地方。而裂隙扩展正是从拉压应力的交界部分开始,而由于裂隙周围应力较难测量,因而,许多学者开始从理论上分析裂纹的扩展方向,并为此提出了最大周向应力准则、最大拉应变准则、最小应变能密度准则、最大能量释放准则、最小J2准则等。
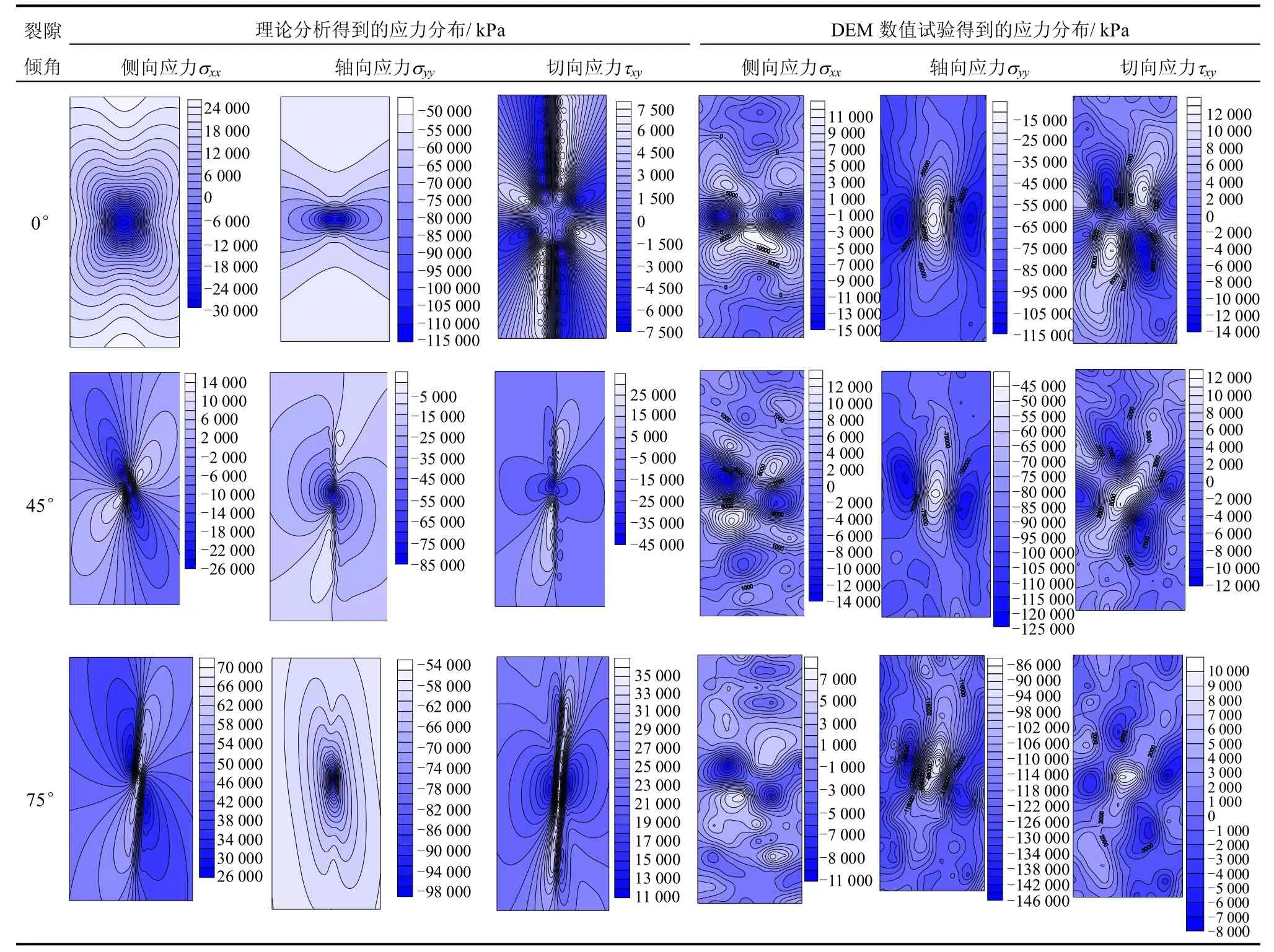
表3 DEM 数值试验和理论分析得到的单裂隙试样应力场Table 3 Stress fields in rock samples containing single flaw obtained from DEM numerical simulations and theoretical analyses
基于图7 中坐标系,岩石受压剪荷载作用时,裂纹尖端的奇异应力在极坐标中应力分量表达式为
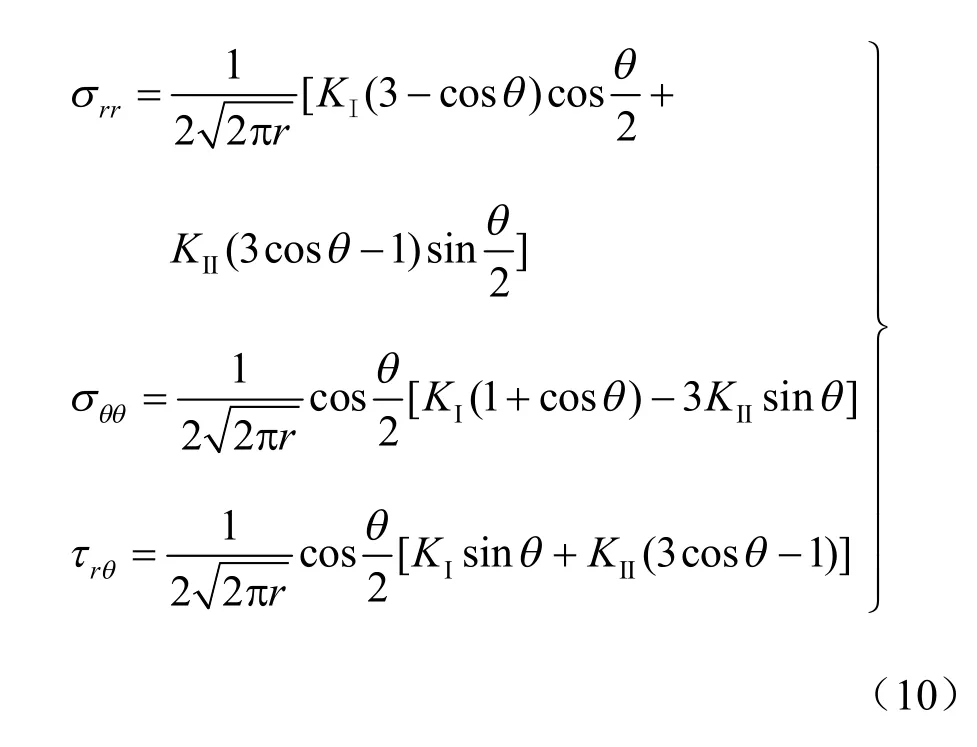
岩石受压剪荷载作用时,裂纹尖端的奇异应力场在笛卡尔坐标系中的应力分量表达式为
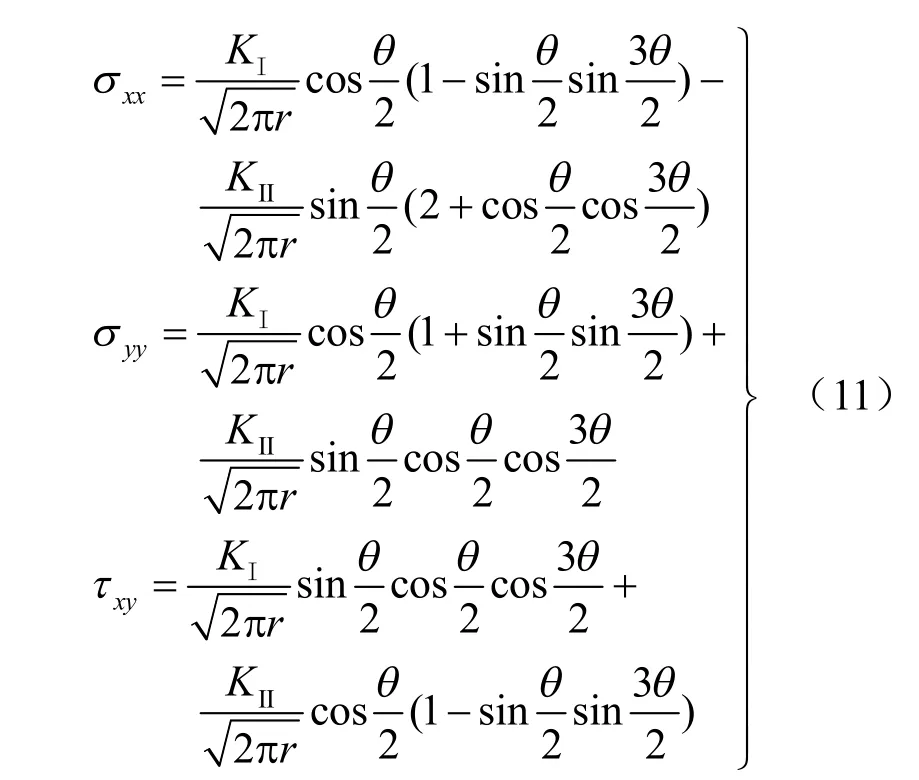
(1)最大周向应力准则[21]
最大周向拉应力准则认为,裂纹沿着最大的周向应力σθθmax扩展,所以该方向满足下列条件:
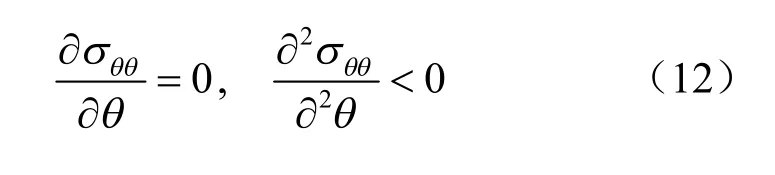
联立式(8)、(9)、(10)、(12)可得到裂纹扩展角为
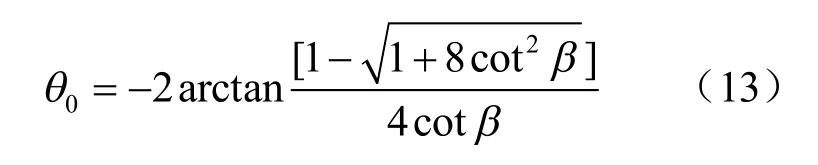
(2)最大拉应变准则[22]
最大拉应变准则认为,环向拉应变 εθθ达到最大值的方向为裂纹扩展方向。对于平面应变问题,由岩石断裂力学可知,裂纹尖端的环向拉应变为
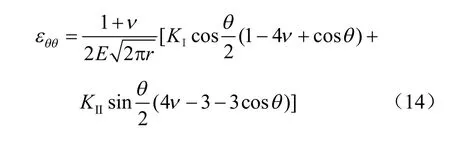
式中:E为弹性模量;ν为泊松比。
将式(8)、(9)代入式(14),推导得到:
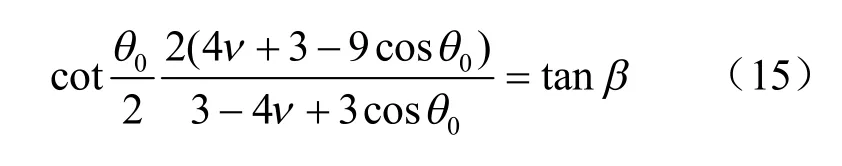
(3)最小应变能密度因子准则[23]
最小应变能密度准则认为,裂纹沿应变能力最小方向发展。由断裂力学可知,单位体积的应变能(又称为应变能密度)为
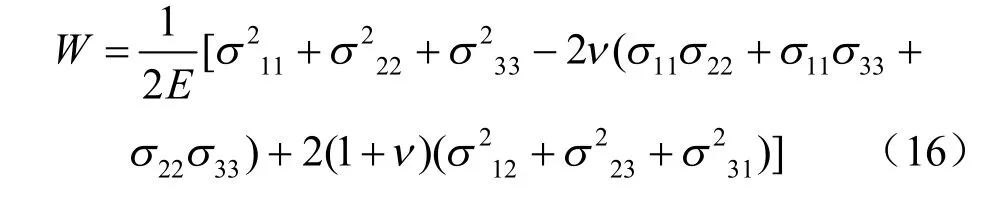
联立式(8)、(9)、(11)、(16),求导得到极小值时裂纹的扩展角θ0为
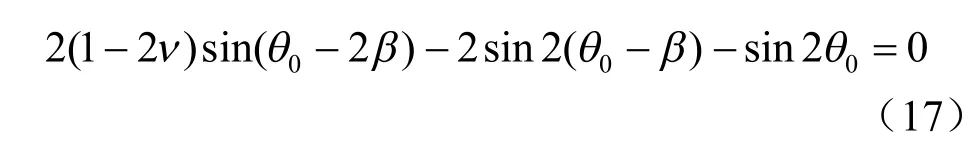
(4)最大能量释放率准则
最大能量释放准则认为,裂纹沿着能量释放率最大的方向扩展,由文献[24]可得到能量释放率G的表达式为
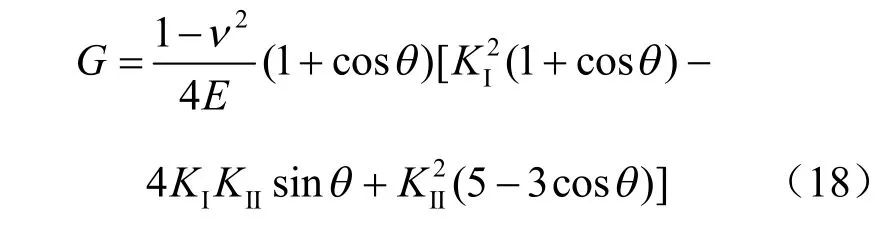
将式(8)、(9)代入式(18),求得G 取极大值时的裂纹扩展角满足:
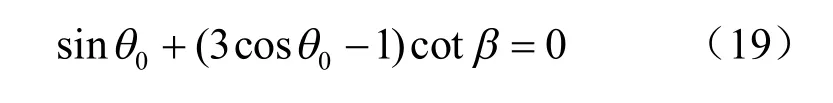
(5)最小J2准则
最小J2准则认为,裂纹沿J2最小的方向扩展,J2的表达式为
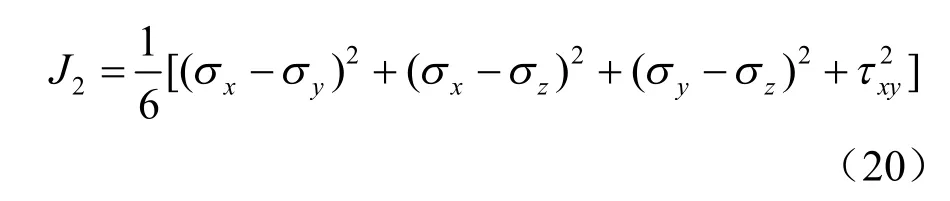
将式(11)代入式(20),求得J2极小值时得到裂纹的起裂角θ0满足[25]:
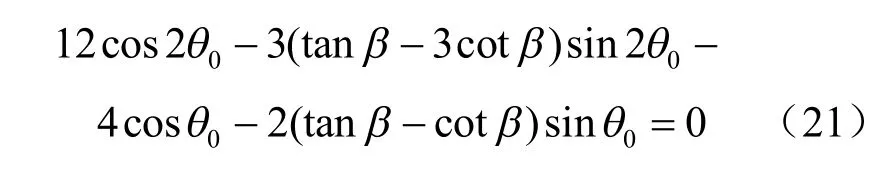
图8为DEM 数值试验、室内试验和理论分析得到的预制裂隙倾角与裂纹起裂角之间的关系。由图可见,三者的结果,裂纹的起裂角均随着预制裂隙倾角的增加而减小;除了最小J2准则之外,其他的理论分析结果与DEM 数值试验及室内试验得到的结果在定性上的一致性良好;DEM 数值试验与室内试验得到的裂纹起裂角在数值上的一致性较好。另外,最大周向应力准则与最大能量释放率准则得到的裂纹起裂角与DEM 数值试验得到的结果较为相似。以上分析表明,最大周向应力准则和最大能量释放率准则在预测裂纹起裂角上较为准确。
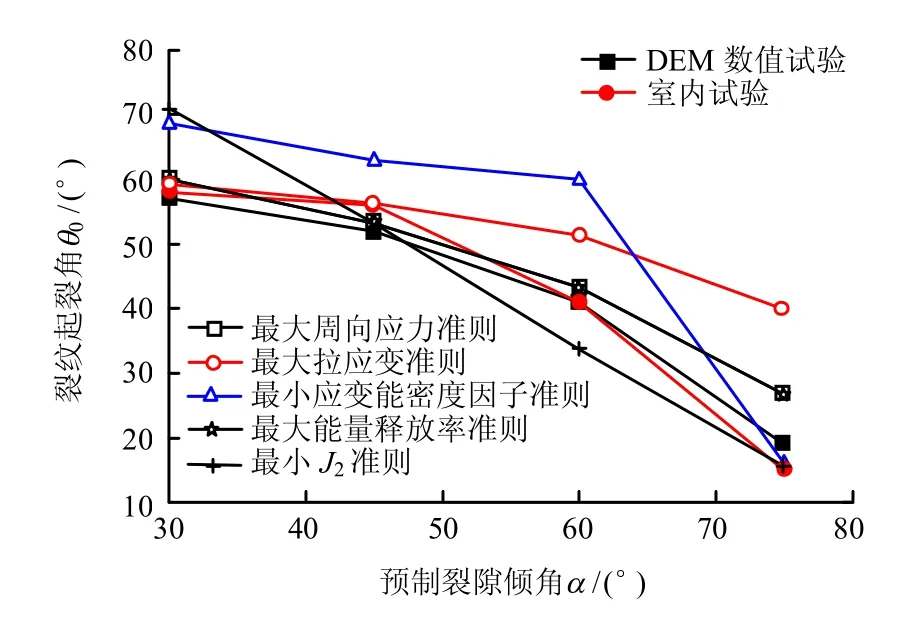
图8 不同方法所得预制裂隙倾角与裂纹起裂角之间的关系Fig.8 Relationships between the pre-existing crack inclination and crack initiation inclination obtained by different methods
5 结 论
(1)由室内试验总结得到的无厚度由抗转动胶结模型适用于模拟岩石裂隙的扩展规律。
(2)与DEM 模拟结果相比,理论分析得到的应力在定性上一致,而在定量上有差距。主要是由于理论分析中假设了岩石为各向同性弹性体,这不能反映真实岩石的非均匀、不连续的特性。当预制裂隙角度较小时,可以观察到明显的应力集中现象:在侧向应力中,裂隙左右两端压应力集中,并由此导致了裂纹上下两面的拉应力集中;而当裂隙角度较大时,裂纹周围的应力集中现象已经不明显,这导致了DEM 结果与理论分析的差别。
(3)DEM 数值试验得到的裂纹起裂角与室内试验得到的结果较一致,且与最大周应力准则和最大能量释放率准则得到的裂纹扩展角较为吻合。
[1]陈卫忠,李术才,朱维申,等.岩石裂纹扩展的实验与数值分析试验[J].岩石力学与工程学报,2003,22(1):18-23.CHEN Wei-zhong,LI Shu-cai,ZHU Wei-shen,et al.Experimental and numerical research on crack propagation in rock under compression[J].Chinese Journal of Rock Mechanics and Engineering,2003 22(1):18-23.
[2]MARTIN C D,CHANDLER N A.The progressive fracture of Lac du Bonnet granite[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1994,31(6):643-659
[3]HEEKWANG L,SEOKWON J.An experimental and numerical study of fracture coalescence in pre-cracked specimen under uniaxial compression[J].International Journal of Solids and Structures,2011,48(6):979-999.
[4]邵冬亮,李术才,李明田,等.单轴压缩下不同裂纹制作方式的裂纹破坏分析及其声发射特征研究[J].山东大学学报(工学版),2011,41(3):131-136.SHAO Dong-liang,LI Shu-cai,LI Ming-tian,et al.Study of failure analysis and the acoustic emission signature of 3-D crack from different origins under uniaxial compression[J].Journal of Shandong University:Engineering Science,2011,41(3):131-136.
[5]LI Y P,CHEN L Z,WANG Y H.Experimental research on pre-cracked marble under compression[J].International Journal of Solids and Structures,2005,42(9):2505-2516.
[6]YANG S D.Experimental study on mechanical behavior of brittle marble samples containing different flaws under uniaxial compression[J].Engineering Fracture Mechanics,2009,76(12):1833-1845.
[7]REYES O,EINSTEIN H H.Failure mechanisms of fractured rock—A fracture coalescence model[C]//Proceedings of 7th International Congress on Rock Mechanics.Germany:Aachen,1991,333-340.
[8]TANG C A.Numerical simulation of progressive rock failure and associated seismicity[C]//International Journal of Rock Mechanics and Mining Sciences.[S.l.]:[s.n.],1997,34(2):249-262.
[9]TANG C A,WONG R H C,CHAU K T,et al.Analysis of crack coalescence in rock-like materials containing three flaws—part II:Numerical approach[J].International Journal of Rock Mechanics &Mining Sciences,2001,38(7):925-939.
[10]IRWIN G R.Analysis of stress and strains near the end of a crack extension force[J].Journal of Applied Mechanics,1957,24:361-364.
[11]李银平,王元汉,陈龙珠,等.含预制裂纹的大理岩的压剪试验分析[J].岩土工程学报,2004,26(1):120-124.LI Yin-ping,WANG Yuan-han,CHEN Long-zhu,et al.Experimental research on pre-existing cracks in marble under compression[J].Chinese Journal of Geotechnical Engineering,2004,26(1):120-124.
[12]陈芳,秦昊.细观尺度下岩石沿晶断裂应力强度因子计算研究[J].岩土力学,2011,32(3):941-945.CHEN Fang,QIN Hao.Study of intercrystalline factures stress intensity factor of rock in meso-scale[J].Rock and Soil Mechanics,2011,32(3):941-945.
[13]蒋明镜,孙渝刚,李立青.水泥胶结颗粒的微观力学模型试验[J].岩土力学,2012,33(5):1293-1299.JIANG Ming-jing,SUN Yu-gang,LI Li-qing.Experimental investigation on micromechanical model of cementbonded particles[J].Rock and Soil Mechanics,2012,33(5):1293-1299.
[14]蒋明镜,周雅萍,陈贺.不同胶结厚度下粒间胶结力学特性的试验研究[J].岩土力学,2013,34(5):1264-1273.JIANG Ming-jing,ZHOU Ya-ping,CHEN He.Experimental study of mechanical behaviors of bonded granules under different bond thickness[J].Rock and Soil Mechanics,2013,34(5):1264-1273.
[15]蒋明镜,陈贺,刘芳.岩石微观胶结模型及离散元数值仿真方法初探[J].岩石力学与工程学报,2013,32(1):15-23.JIANG Ming-jing,CHEN He,LIU Fang.A microscopic bond model for rock and preliminary study of numerical simulation method by distinct element method[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(1):15-23.
[16]JIANG M J,YU H S,HARRIS D.A novel discrete model for granular material incorporating rolling resistance[J].Computers and Geotechnics,2005,32(5):340-357.
[17]JIANG M J,YU H S,HARRIS D.Bond rolling resistance and its effect on yielding of bonded granulates by DEM analyses[J].International Journal for Numerical and Analytical Methods in Geomechnics,2006,30(8):723-761.
[18]JIANG M J,KONRAD J M,LEROUEIL S.An efficient technique for generating homogeneous specimens for DEM studies[J].Computers and Geotechnics,2003,30(7):579-597.
[19]蒋明镜,陈贺.预制单裂隙岩石的裂纹扩展机制的离散元数值分析[J].岩石力学与工程学报,在审.JIANG Ming-jing,CHEN He.Distinct element analysis of crack propagation in rocks containing pre-existing single flaws[J].Chinese Journal of Rock Mechanics and Engineering,under review.
[20]WESTERGAARD H M.Bearing pressures and cracks[J].Journal of Applied Mechanics,1939,61:49-53.
[21]PARIS P C,ERDOGAN F.A critical analysis of crackpropagation laws[J].Journal of Fluids Engineering,1963,85(4):528-533.
[22]MAZARS J,PIJAUDIER C G.Continuum damage theory—Application to concrete[J].Journal of Engineering Mechanics(ASCE),1987,115(2):345-365.
[23]SIH G C,BARTHELEMY B M.Mixed mode fatigue crack growth predictions[J].Engineering Fracture Mechanics,1980,13:439-451.
[24]崔德渝,吴绍富,张行.复合裂纹的能量释放率计算与断裂判据[J].北京航空航天大学学报,1990,3:43-49.CUI De-yu,WU Shao-fu,ZHANG Xing.Energy release rate and failure criterion for mixed mode cracking[J].Journal of Beijing University of Aeronautics and Astronautics,1990,3:43-49.
[25]周家文,徐卫亚,石崇.基于破坏准则的岩石压剪断裂判据研究[J].岩石力学与工程学报,2007,26(6):1194-1201.ZHOU Jia-wen,XU Wei-ya,SHI Chong.Investigation on compression-shear fracture criterion of rock based on failure criteria[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(6):1194-1201.
