地铁行车速度对盾构隧道运营沉降的影响分析
2015-02-17高广运
姜 洲,高广运,赵 宏
(1.安徽省综合交通研究院股份有限公司,安徽 合肥 230001;2.同济大学 岩土及地下工程教育部重点实验室,上海 200092)
1 引 言
软土盾构隧道的运营沉降问题涉及到土的性质、隧道渗漏水、列车荷载及周围环境条件等多种因素[1],是一个非常复杂的课题。其中,地铁行车荷载经轨道-道床-隧道结构传至下卧土层,在土体内部产生的循环动应力以及超孔隙水压力是引起盾构隧道沉降重要原因。尤其是在东南沿海一带广泛分布着深厚软黏土地区,地铁行车荷载诱发的地基塑性累积变形以及局部差异沉降等问题越来越受到关注[2]。监测发现,上海地铁建成投付使用后,行车荷载对隧道周围土体强度和变形的影响较大,而这种影响与列车运行状态有很大的相关性[3]。当隧道存在不均匀沉降时,两者相关性更为突出。如上海地铁一号线运营至今某区间隧道纵向差异沉降已超过10 cm,且许多段的沉降一直在发展,局部差异沉降常导致轨道的不平顺[4]。某试验表明,在平顺轨面上,行车速度从10 km/h 提高到100 km/h 时,动应力只增加7%;而当轨面存在长60 mm、深3 mm的不平顺时,在同样的情况下,动应力增加1.5 倍,这将进一步加剧轨道的破坏及地基的沉降[5]。
目前软土盾构隧道运营沉降预测方法主要包括:现场测试法[6]、经验法[7]、数值模拟法[8]、解析法[9]、模型试验[10]等,其影响因素的研究重点在隧道下卧土层的性质、隧道结构渗漏水以及周围环境的变化等方面,而关于地铁行车荷载影响的研究较少。刘明等[11]采用拟静力有限元计算和经验拟合计算模型相结合的方法预测地铁荷载作用下饱和软黏土的长期沉降,计算结果得到了较好的验证。黄茂松等[12]对饱和软黏土在等压和偏压固结两种循环加载情况下累积变形特性开展研究,提出了计算轴向循环塑性累积应变的显式模型。姜洲等[2]进一步研究偏压固结条件下循环加载轴向塑性累积应变的发展规律,改进经验模型,对车载下上海某地铁区间隧道的长期沉降进行预测。高广运等[13]建立三维数值模型,结合3 种不同的塑性累积应变经验算法,计算地铁循环荷载作用下轨道地基的长期沉降。可见,车载下地铁隧道长期沉降主要通过经验公式进行预测,公式参数一般由试验或数值模型计算得到。
对于车载下地铁隧道长期沉降的研究多是对循环荷载作用下地基塑性累积应变经验计算公式进行改进,而对地铁行车速度与隧道长期沉降相关性的研究较少,特别是未见关于隧道存在差异沉降时地铁行车速度对隧道运营沉降的影响研究。周萌等[14]建立三维有限元模型,分析移动荷载作用,不同路基不均匀沉降幅值对板式轨道混凝土构件动力特性的差异影响。宋波等[15]建立车轨耦合分析模型,分析了高速铁路不同路基沉降分布特征、不同列车运行速度条件下车辆和轨道振动特性,发现路基无沉降变形时,列车运行速度对轮轨接触力响应最值影响较小,而存在不均匀沉降分布时,随着列车速度的增加,轮轨接触力和车体加速度都明显增加。
笔者在文献[2,4]中分别对车载下隧道长期沉降的预测方法及地基差异沉降对地铁隧道结构的影响展开讨论,本文的研究在二者的基础上展开,以上海地铁一号线上海体育馆站附近区间隧道为工程背景,对比分析盾构隧道下卧土层有、无纵向差异沉降两种情况下,地铁列车运行速度对隧道运营沉降的影响。
2 差异沉降对地铁行车荷载的影响
2.1 车-轨-隧道-地基竖向耦合动力模型
假定隧道衬砌与下卧土体不会因为局部不均匀沉降而脱空,建立车-轨-隧道-地基竖向耦合动力模型[4],分析地铁隧道纵向不均匀沉降对行车荷载及隧道运营的不利影响。
该模型可以分解为:车辆模型、轨道-道床模型、地基土模型。其中,车辆系统简化为由车体-构架-轮对组成的多刚体系统,彼此间通过二系弹簧-阻尼元件连接,以1/4 车体为研究对象,如图1 所示。钢轨结构模型采用连续弹性支承梁模型,地基简化为弹性半空间,轨道与隧道下卧土体相互作用的力学示意图如图2 所示。图中,mc为车体质量,mb为转向架质量,mw为轮对质量,uc、ub、uw分别为车厢、转向架和轮对的竖向位移,以向下为正方向,ks1,dp1,ks2,dp2分别为二系弹簧和阻尼。

图1 列车荷载简化计算模型[4]Fig.1 Simplified calculation model of train load

图2 轨道-地基耦合系统简化模型[4]Fig.2 Simplified model of track-subgrade coupled system
(1)车辆系统控制方程为

(2)轨道-道床模型控制方程为

式中:

(3)假定隧道下卧土体为各向同性均质弹性体,忽略体力,引入动力微分方程[16]:

式中:∇表示求散度;U(x,y,z,t)={u1,u2,u3}为半空间土体的位移向量,沿x、y、z 轴的位移分别用u1、u2、u3表示;是U 对时间t 的二阶导数;λ 和μ为半空间土体Lame 常数;ρs为土体密度。
假定地基不均匀沉降导致的轨道变形呈余弦分布,如图3 所示。

图3 隧道地基差异沉降模型[4]Fig.3 Differential settlement model of tunnel subgrade
以列车行进方向为x 轴正方向,地基局部不均匀沉降处轨面外形用式(4)表示:

式中:l为沉降槽长度;H为槽深;x0表示列车行进方向沉降槽边缘所在位置。取坐标原点为列车运动起点,车轮竖向位移uw与轨道在x=tν 位置处的竖向位移ur间关系可以表示为

隧道下卧土体的边界条件为

式中:σ为土体应力函数;2a为道床下部隧道与土体接触面垂直于轨道方向的等效宽度。
定义对时间t 的Fourier 变换及其逆变换为

定义对x,y 坐标的Fourier 变换及其逆变换为

联立方程(1)~(6),并结合拉梅公式,通过Fourier 变换求解,得到位移函数ur,ut在波数-频率域内的解,如式(9),(10)所示。
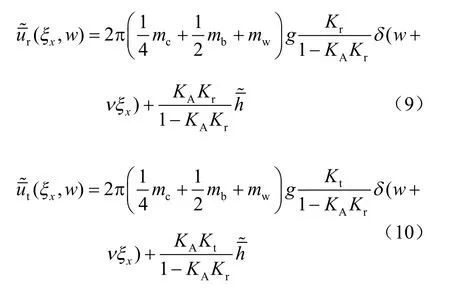
式中:参数KA、Kr、Kt的计算详见文献[4]。两式中前半部分反映车辆荷载对轨道和隧道变形的影响,后半部分反映纵向不均匀沉降的影响。分别对式(9),(10)进行Fourier 逆变换,得轨道与地基位移函数 ur(x,t) 和 ut(x,t) 。
轨下支撑力Fs即可表示为

2.2 模型验证
为对比分析有、无差异沉降两种情况下,差异沉降对列车运行速度的影响,通过退化模型验证本式计算的准确性。将模型退化为连续支撑的单层Euler 梁模型,三自由度车体模型简化为单位移动荷载。计算中取轨面不平顺参数h=0,移动荷载为单位质量,速度为70 m/s。轨道参数采用法国TGV轨道参数,地基参数见表1。计算结果如图4 所示。

表1 轨道、地基参数[17]Table 1 Parameters of track and foundation

图4 退化模型对比验证Fig.4 Comparison and validation of degradation model
由图可见,退化模型计算结果与王国波[17]计算结果较为接近,数值偏大是因为文献[17]中地基为7 m 厚黏弹性层加刚性地基,与本文假设地基为弹性半空间不同。
2.3 计算结果与分析
上海地铁一号线采用弹性支撑块结构,隧道内采用钢筋混凝土整体道床,混凝土强度等级为C30,轨枕采用C50 钢筋混凝土轨枕。列车为二系悬挂的A 型车。列车最高行驶速度为80 km/h,运营速度为35 km/h。本文计算中,取土体参数E=7.3 MPa,v=0.4,ρ=1 700 kg/m3。以单轮对为分析对象,地铁列车系统、轨道计算参数如表2、3 所示。

表2 地铁车辆参数[18]Table 2 Parameters of metro vehicle

表3 轨道计算参数[18-19]Table 3 Calculation parameters of track
基于车-轨-隧道-地基竖向耦合动力模型,分析隧道纵向不均匀沉降对地铁行车荷载的影响。隧道不均匀沉降槽长度l=20 m,分别取槽深H=0.005、0.01、0.015、0.02 m,当列车运行速度v=18,36,54,72 km/h 时,钢轨支撑反力峰值随地铁行车速度变化情况如图5 所示。轨下支撑反力峰值随沉降槽深变化情况如图6 所示。当H=0.01 m 时,在单轮载作用下,隧道下卧土体竖向变形随行车速度的变化情况,如图7 所示。

图5 列车速度的影响曲线Fig.5 Influence curves of train speed
由图5、6 可见,列车荷载作用下,轨下支撑反力随着列车运行速度的增大而增加,当沉降槽深H=0.01 m 时,列车运行速度由18 km/h 增加到72 km/h 时,轨下支撑反力峰值增大近8.5%。当槽深为H=0.02 m 时,轨下支撑反力峰值将增大近17.4%。可见随着列车速度增大,沉降槽的影响也愈加明显。由图7 中隧道下卧土体竖向变形时程曲线可以看出,列车运行速度越快,下卧土体波动越大,但衰减越快,列车荷载作用时间及沿运行方向影响范围越小。

图6 沉降槽的影响曲线Fig.6 Influence curves of settlement trough

图7 土体竖向变形时程曲线Fig.7 Time history curves of soil vertical deformation
3 行车速度对地铁运营沉降的影响
3.1 长期沉降预测方法
以上海地铁一号线上海体育馆站附近区间隧道为工程背景建立三维数值模型。首先由车-轨-隧道-地基竖向耦合动力模型计算轨下支撑力,模拟列车荷载,施加在已建立的FLAC3D数值模型上,通过计算得到第1 次加载土体的应力水平,求得第一次循环塑性应变和孔压,运用循环荷载下软黏土累积塑性应变及累积孔压计算模型,结合分层总和法,计算隧道长期沉降。
(1)计算模型及边界条件
上海地铁一号线隧道直径D为6.2 m,体育馆站附近区间隧道覆土厚近8 m,基本位于第④层淤泥质黏土中。参考高广运等[13]模型,取模型尺寸为80 m(x)×60 m(y) ×60 m(z),其中水平x 方向为隧道轴线方向,长度取为80 m;水平y 方向为垂直于隧道轴线方向,取60 m,略小于10D;z 方向为竖直向,取60 m,大于7 倍上覆土深度。
在地表下10.8 m 处盾构开挖,开挖半径为3.1 m,并施加衬砌,衬砌厚度35 mm,为C55 混凝土,采用结构单元中的壳单元模拟;在隧道中心处以下2.2 m 处建立道床模型,采用壳单元模拟,材料为C30 混凝土,材料参数取值见表4;然后消除道床实体模型,得到以结构单元模拟的垫层。模型考虑列车荷载引起的孔隙水压力变化,采用FLAC3D中“干法”进行不排水分析,水位取z=0。土体分层情况以及相关参数取值见表5,三维数值模型如图8 所示。

表4 材料参数[13]Table 4 Parameters of material

表5 土层参数[20-21]Table 5 Parameters of soil layers

图8 三维计算模型Fig.8 Three-dimensional calculation model
土体以摩尔-库仑模型模拟,模型静力分析时,边界条件为:上表面自由,底部固定,四周水平向固定,竖向自由。动力分析时引入人工黏性边界,以避免波的反射[13]。
(2)列车荷载的模拟及加载
结合2.1节中车-轨-隧道-地基竖向耦合动力模型,计算列车荷载作用下轨道道床接触点荷载时程曲线,如图9 所示。

图9 轨下支撑力时程曲线Fig.9 Time history curves of support force under rail
将作用在道床上的轨下支撑反力均匀地分配到三维数值模型的各节点位置,以此进行模型的受力分析。采用这种加载方法,不需要在数值模型中铺设轨道,能够简化数值模型,节省计算时间,同时能够减弱模型对列车荷载作用点位置的约束。加载过程通过FISH 语言编写函数实现。列车轮轨力分布及网格点受力示意图如图10 所示,三维模型实际加载如图11 所示。

图10 轮轨力分布及网格节点受力示意图Fig.10 Sketch of wheel-rail contact forces and grid nodes

图11 荷载施加情况Fig.11 Condition of the applied force
(3)经验计算模型
基于K0固结条件下软黏土累积塑性应变公式与累积孔压公式分别计算循环动应力及超孔隙水压力消散引起的地基沉降,参数由试验和三维有限差分模型分析得到。
其中,塑性累积应变模型[2]为

累积孔压计算公式[22]为

式中:参数a、m、c 反映了动偏应力水平以及初始固结条件对第1 次循环塑性累积应变的影响;b(b1、b2)反映了循环次数、初始固结条件(等向、偏压)对轴向循环塑性累积应变的影响;Pa=101 kPa,用于归一化处理;Dd反映动偏应力水平;P为初始平均固结应力;参数au、mu反映动偏应力水平对第1次循环累积孔压与围压归一化值的影响;cu反映围压对第1 次循环累积孔压的影响;bu反映循环次数对循环累积孔压的影响。各参数的取值参见文献[2]及文献[22]。
孔压消散采用一维Terzaghi 固结方程求解,结合分层总和法,分别求得不排水循环荷载作用下土体累积变形引起的沉降以及动荷载引起的孔隙水压力消散产生的固结沉降,二者相加得到地铁列车动荷载作用下软土地基沉降。
3.2 行车速度对隧道沉降的影响分析
基于前述模型及计算方法,对比分析盾构隧道下卧土层有、无纵向差异沉降两种情况下地铁行车速度对隧道运营沉降的影响。以隧道轴线中部(即x=40 m,y=0 m)土体为分析对象。
(1)沉降槽深H=0

图12 超孔隙水压力时程曲线Fig.12 Time history curves of excessive pore water pressure
首先分析列车运行速度对孔隙水压力的影响,如图12 所示。当列车速度由10 m/s 增加到20 m/s时,距离隧道底部1 m处孔隙水压力峰值由3.1 MPa增加到3.2 MPa。可见,列车运行速度越快,隧道下卧土层中超静孔隙水压力越大,超孔压波动亦越大,但持续时间相对较短,变化速率快。
图13 反映列车一次运行导致下卧土体的弹性变形和塑性变形情况,由图可知,列车运行速度对隧道下卧土体变形有较明显的影响。分别取列车运行速度v=10、20、30 m/s,对应距离隧道底部1 m处,下卧土体弹塑性变形峰值分别为2.39、2.22、2.16 mm。而距离隧道底部6.5 m 处土体弹塑性变形峰值分别为1.97、1.88、1.77 mm。可见,与孔隙水压力呈现的规律相反,随着列车运行速度的增大,下卧土体的变形反而有一定程度的减小。当列车运行速度由10 m/s 增加到30 m/s 时,下卧土体的弹塑性变形量减小近10%。

图13 列车运行速度对下卧土体变形的影响Fig.13 Time history curves of foundation deformation of lying soil

图14 列车运行速度对长期沉降的影响Fig.14 Influence of train speed on long-term settlement
进而分析列车运行速度与隧道长期沉降之间的关系,如图14 所示。当列车运行速度由10 m/s 增加大20 m/s 时,隧道5、10、20年累积沉降将分别由13.73、17.86、23.24 mm 减小到13.17、17.13、22.29 mm。可见,随着列车运行速度的增加,地铁隧道长期沉降减小。其原因是列车速度越快,虽然轮轨力有所增加,但荷载的作用时间相对短,对土体的扰动相对较小。此结论和高广运等[23]建立的交叉隧道的三维有限差分模型,以人工数定激励力模拟列车荷载,分析地铁循环荷载作用下交叉隧道的沉降规律得到的相关结论一致。计算中的荷载为理想条件下的列车运行荷载,未考虑轨道局部突出不平顺条件及隧道局部差异沉降等不利因素的影响。
(2)沉降槽深H=10 mm
假定盾构隧道初始运行阶段存在长度l=20 m,槽深H=10 mm 的差异沉降区域,范围为隧道轴线沿列车运行方向(x 方向)30~50 m。通过施加轨下支撑反力的大小反映隧道局部不均匀沉降区域的影响。由图6 可知,当v=20 m/s 时,施加在数值模型沉降槽中心位置上的荷载较无差异沉降情况大9.2%,而沉降槽边缘位置为0,其间近似为直线变化。三维数值模型荷载施加情况如图11 所示。
由图6 可知,v=10 m/s 时,沉降槽深H 由0增加到10 mm,车辆运行荷载仅增大1.3%,对隧道下卧土体的竖向位移及超孔隙水压力影响较小,因此,不作详细说明。在此重点分析v=20 m/s,列车运行一次,隧道下卧土体的竖向位移及超孔隙水压力变化规律,如图15、16 所示,监测距离隧道底部1,2,6.5,11,30 m 处土层变形及超孔压变化情况。由图15 可见,距离隧道底部1 m 处土层峰值位移达2.4 mm,较隧道无局部不均匀沉降时的数值2.3 mm 大4.3%。由图16 可见,隧道底部1 m 和2 m处超孔压峰值分别为3.4 kPa、2.2 kPa,相比较无局部不均匀沉降的数值3.2 kPa、2.0 kPa 分别大6.3%和10%。结果表明:当地铁隧道运行列车通过存在局部差异沉降的区域时,下卧土体的竖向位移以及超孔隙水压力峰值均较通过无差异沉降区域时有一定程度的增加。

图15 下卧土体竖向位移时程曲线(H=10 mm)Fig.15 Time history curves of vertical displacement of lying soil

图16 超孔隙水压力变化时程曲线(H=10 mm)Fig.16 Time history curves of excessive pore water pressure
由图17 可知,当沉降槽长l=20 m,深H=10 mm,列车以v=20 m/s 的速度行驶时,隧道在运营5、10、20年后的长期沉降分别为:14.21、18.49、24.06 mm。相比较H=0 时,地铁隧道运营20年后沉降增加8%;受地铁隧道局部差异沉降的影响,隧道下卧土体累积变形引起的沉降以及超孔隙水压力消散产生的固结沉降均有一定程度的增加;隧道纵向不均匀沉降对其长期运营有明显不利影响。

图17 隧道地基长期沉降与运营时间关系Fig.17 Relationships between long-term settlement of tunnel foundation and service time
图18 对比分析盾构隧道下卧土层有、无纵向差异沉降两种情况下地铁行车速度对隧道运营沉降的影响。当存在沉降槽深H=10 mm 时,地铁运行速度越快,隧道下卧地基长期沉降越大,与H=0理想条件下计算结论相反,更符合地铁隧道实际运营情况,同时可为列车速度调控方式的选择提供参考,即在差异沉降较大的位置,应减小列车运行速度,以控制地基沉降发展,保证地铁隧道长期安全运营。

图18 列车运行速度对长期沉降的影响分析Fig.18 Influence of train speed on long-term settlement
4 讨 论
软土盾构隧道运营期间,列车运行速度是诱发地基沉降的主要因素之一,本文在分析过程中未涉及渗漏水、周围环境变化等多因素的协同作用,因此,可进一步分析各沉降影响因素的相关性,综合考虑各因素对隧道运营沉降的影响;实际情况中隧道局部不均匀沉降在不断发展,以不变的沉降槽模型来描述其特性较为粗糙,应尝试引入考虑隧道差异沉降动态变化的新模型以更符合实际情况。由于目前长期监测数据较少,建议多进行隧道结构变形的长期实时监测,同时多开展现场试验,积累更多的实测数据及试验数据,以验证理论研究和数值模拟的正确性。
5 结 论
(1)随着列车运行速度增大,隧道差异沉降的影响愈加明显;轨下支撑力随着列车运行速度的增大而增加,列车运行速度越快,下卧土体波动越大,但衰减越快。
(2)受地铁隧道局部差异沉降的影响,隧道下卧土体累积变形引起的沉降以及超孔隙水压力消散产生的固结沉降均有一定程度的增加;隧道纵向不均匀沉降对其长期运营有明显不利影响。
(3)当隧道差异沉降小、轨道不平顺条件较好时,地铁行车速度越快,荷载作用时间短,对下卧土层的扰动小,隧道运营沉降越小。
(4)当地基差异沉降突出,轨道存在明显不平顺时,隧道运营沉降随行车速度增大而显著增加。因此,在隧道差异沉降较大的位置,应减小列车运行速度,以控制地基沉降的发展,保证地铁隧道长期安全运营。
[1]张震.盾构隧道结构长期沉降研究综述[J].城市轨道交通研究,2013,3:135-140.ZHANG Zhen.On the long-term settlement of shield tunnel structure[J].Urban Mass Transit,2013,3:135-140.
[2]姜洲,高广运,赵宏,等.软土地区地铁行车荷载引起的隧道长期沉降分析[J].岩土工程学报,2013,(增刊2):301-307.JIANG Zhou,GAO Guang-yun,ZHAO Hong,et al.Long-term settlement of tunnels induced by subway moving load in soft soil districts[J].Chinese Journal of Geotechnical Engineering,2013,(Supp.2):301-307.
[3]唐益群,赵化,王元东,等.地铁荷载下隧道周围加固软黏土应变累积特性[J].同济大学学报(自然科学版),2011,39(7):972-977.TANG Yi-qun,ZHAO Hua,WANG Yuan-dong,et al.Characteristics of strain accumulation of reinforced soft clay around tunnel under subway vibration loading[J].Journal of Tongji University(Nature Science),2011,39(7):972-977.
[4]姜洲,高广运,戴海峰,等.车载下地基差异沉降对地铁隧道结构的影响分析[J].地下空间与工程学报,2014,6:1433-1439.JIANG Zhou,GAO Guang-yun,DAI Hai-feng,et al.Influence of differential subgrade settlement on metro tunnel structure under train load[J].Chinese Journal of Underground Space and Engineering,2014,6:1433-1439.
[5]童大埙.铁路轨道基本知识[M].北京:中国铁道出版社,1997:226.TONG Da-xun.Basic knowledge of railway track[M].Beijing:China Railway Publishing House,1997.
[6]魏新江,葛国宝,丁智,等.基于智能单粒子算法的地铁隧道工后长期沉降预测[J].武汉理工大学学报,2012,34(12):89-92.WEI Xin-jiang,GE Guo-bao,DING Zhi,et al.Application of intelligent single particle optimizer in predicting long-term surface settlement after subway construction[J].Journal of Wuhan University of Technology,2012,34(12):89-92.
[7]沈礼伟,庄海洋,陈 磊,等.列车振动荷载作用下南京细砂累积变形预测公式对比分析[J].岩土力学,2014,35(11):3170-3176.SHEN Li-wei,ZHUANG Hai-yang,CHEN Lei,et al.Prediction formula for dynamic accumulated deformation of Nanjing fine sand under train-induced vibration load[J].Rock and Soil Mechanics,2014,35(11):3170-3176.
[8]杨茜,张顶立,刘志春.局部荷载作用下软土盾构隧道纵向沉降数值分析[J].北京工业大学学报,2012,38(8):1220-1224.YANG Qian,ZHANG Ding-li,LIU Zhi-chun.Numerical simulations of longitudinal settlement of shield tunnel under local loading[J].Journal of Beijing University of Technology,2012,38(8):1220-1224.
[9]张冬梅,刘印,黄宏伟.软土盾构隧道渗流引起的地层和隧道沉降[J].同济大学学报(自然科学版),2013,41(8):1185-1190,1212.ZHANG Dong-mei,LIU Yin,HUANG Hong-wei.Leakage-induced settlement of ground and shield tunnel in soft clay[J].Journal of Tongji University(Natural Science),2013,41(8):1185-1190,1212.
[10]马险峰,余龙,李向红.不同下卧层盾构隧道长期沉降离心模型试验[J].地下空间与工程学报,2010,6(1):14-20.MA Xian-feng,YU Long,LI Xiang-hong.Centrifuge modeling of longitudinal long-term settlement of shield tunnels overlying transitional ground[J].Chinese Journal of Underground Space and Engineering,2010,6(1):14-20.
[11]刘明,黄茂松,李进军.地铁荷载作用下饱和软黏土的长期沉降分析[J].地下空间与工程学报,2006,2(5):813-817.LIU Ming,HUANG Mao-song,LI Jin-jun.Long-term settlement of saturated soft clay under subway loading[J].Chinese Journal of Underground Space and Engineering,2006,2(5):813-817.
[12]黄茂松,姚兆明.循环荷载下饱和软黏土的累积变形显式模型[J].岩土工程学报,2011,33(3):325-331.HUANG Mao-song,YAO Zhao-ming.Explicit model for saturated clay behavior subjected to cyclic loading[J].Chinese Journal of Geotechnical Engineering,2011,33(3):325-331.
[13]高广运,徐大为,张先林,等.地铁循环荷载作用下上海软土路基的长期沉降计算[J].桂林理工大学学报,2012,32(3):370-374.GAO Guang-yun,XU Da-wei,ZHANG Xian-lin,et al.Long-term settlement calculation of Shanghai metro soft soil foundation under cyclic loading[J].Journal of Guilin University of Technology,2012,32(3):370-374.
[14]周萌,宫全美,王炳龙,等.路基不均匀沉降值对板式轨道动力响应的影响[J].铁道标准设计,2010,42(10):1-4.ZHOU Meng,GONG Quan-mei,WANG Bing-long,et al.Influence of uneven sedimentation value of subgrade on dynamic response of slab tracks[J].Railway Standard Design,2010,42(10):1-4.
[15]宋欢平,边学成,蒋建群,等.高速铁路路基沉降与列车运行速度关联性的研究[J].振动与冲击,2012,31(10):134-140.SONG Huan-ping,BIAN Xue-cheng,JIANG Jian-qun,et al.Correlation between subgrade settlement of highspeed railroad and train operation speed[J].Journal of Vibration and Shock,2012,31(10):134-140.
[16]胡安峰,伍云利,孙波,等.高速列车荷载作用下无砟轨道—地基竖向耦合动力响应研究[J].工程力学,2012,29(3):237-243.HU An-feng,WU Yun-li,SUN Bo,et al.Study on vertical dynamic response of ballastless track and subgrade of high-speed train loads[J].Engineering Mechanics,2012,29(3):237-243.
[17]王国波.移动荷载作用下地基土动力响应计算方法的研究[D].武汉理工大学,2003.WANG Guo-bo.The study of calculation method on dynamic response of soil induced by moving loads[D].Wuhan:Wuhan University of Technology,2003.
[18]宫全美,徐勇,周顺华.地铁运行荷载引起的隧道地基土动力响应分析[J].中国铁道科学,2005,26(5):47-51.GONG Quan-mei,XU Yong,ZHOU Shun-hua.Dynamic response analysis of tunnel foundation by vehiclevibration in metro[J].China Railway Science,2005,26(5):47-51.
[19]袁俊.地铁浮置板轨道结构减振研究[D].西安:西安建筑科技大学,2008.YUAN Jun.Study on vibration isolation performance of the floating slab track system in metro lines[D].Xi′an:Xi′an University of Architecture and Technology,2008.
[20]张治国,黄茂松,王卫东.隧道开挖对层状地基中邻近管道影响的DCBEM-FEM耦合方法[J].岩土工程学报,2011,33(10):1554-1561.ZHANG Zhi-guo,HUANG Mao-song,WANG Wei-dong.DCBEM-FEM coupling method for response analysis of adjacent pipelines due to tunneling[J].Chinese Journal of Geotechnical Engineering,2011,33(10):1554-1561.
[21]孔祥鹏,刘国彬,廖少明.明珠线二期上海体育馆地铁车站穿越施工对地铁一号线车站的影响[J].岩石力学与工程学报,2004,23(5):821-825.KONG Xiang-peng,LIU Guo-bin,LIAO Shao-ming.Influence of construction of Shanghai stadium transverse station of pearl line phase Ⅱ on station of metro line No.1[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(5):821-824.
[22]姚兆明,张明慧,陈军浩.饱和软黏土循环累积孔压模型及地铁隧道路基长期沉降计算[J].铁道学报,2012,34(9):87-92.YAO Zhao-ming,ZHANG Ming-hui,CHEN Jun-hao.Cyclic accumulative pore pressure explicit model of saturated soft clay and long-term settlement calculation of subway tunnel roadbed[J].Journal of the China Railway Society,2012,34(9):87-92.
[23]高广运,李绍毅,涂美吉,等.地铁循环荷载作用下交叉隧道沉降分析[J].岩土力学,2015,36(增刊1):486-490.GAO Guang-yun,LI Shao-yi,TU Mei-ji,et al.Analysis of settlement of cross tunnels under cyclic metro loading[J].Rock and Soil Mechanics,2015,36(Supp.1):486-490.
