基于组合指数型流变模型的堆石坝流变分析

黄耀英，包腾飞，田 斌，郑 宏

（1.三峡大学 水利与环境学院，湖北 宜昌 443002；2.河海大学 水利水电学院，江苏 南京 210098；3.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，湖北 武汉 430071）

1 引 言

堆石坝实测资料表明，堆石坝的变形大都在建成后若干年才逐渐沉降稳定，因此，一般选用随时间衰减的流变模型来反映堆石料的流变特性。依据堆石料的流变试验，沈珠江等[1]对西北口垫层料进行了流变试验，提出了3 参数指数流变模型，由于该模型具有一定的物理意义，且模型简单，易于进行数值分析，在工程界得到了广泛应用。郭兴文等[2]对高围压下3 参数指数流变模型中的最终体积流变量进行了修正。米占宽等[3]根据公伯峡主堆石料室内流变试验资料，采用6 参数指数流变模型模拟堆石料的流变规律。李国英等[4]，方维凤[5]采用大型三轴仪对公伯峡面板堆石坝坝内3 种主要堆石料的流变特性进行了试验研究，采用7 参数指数流变模型模拟堆石料的流变规律；程展林等[6]针对水布垭面板堆石坝主堆石料茅口组灰岩和次堆石料栖霞组灰岩，采用应力式大型三轴仪进行了系统试验，提出了9 参数幂函数流变模型。周伟等[7]在9 参数堆石流变模型的基础上提出了适用于高围压下的幂函数流变本构模型。此外，沈凤生等[8]采用一个三元件黏弹性模型（Merchant 模型）考虑面板堆石坝的流变变形。蔡新等[9]采用Maxwell 模型和H-K 模型对梅溪面板堆石坝进行了计算分析。

谢腊德、库克等[10]对碾压堆石面板坝开始蓄水后坝顶沉降量进行了统计分析，他们认为，碾压堆石面板坝坝顶沉降小、收敛快，折算成100 m 高堆石坝的收敛率，在蓄水5 a 后，碾压面板坝约为3.5 mm/a，10 a后约为1.5 mm/a，30 a后约为0.6 mm/a。由于无论是3 参数、6 参数和7 参数指数流变模型，还是Merchant 模型或H-K 模型，均仅有一个指数式进行流变收敛率调节，难以同时合理地反映蓄水初期和蓄水后期的沉降变化规律；虽然9 参数幂函数流变模型可以较好地反映堆石坝的沉降变化规律，但数学运算较复杂。目前，室内堆石料流变试验一般试验历时1 个月左右，采用一个指数式进行流变收敛率调节的缺点不明显。由于不能合理反映堆石坝的沉降变化规律，导致不能准确预测后期流变引起的面板顶部脱空及防浪墙底部架空等情况。

混凝土热学力学性能是混凝土龄期的函数，目前有指数式、双曲线式和双指数式等表达式，指数式便于进行数学运算，但与试验资料吻合得不好，双曲线式和双指数式与试验资料吻合得较好，但不便于进行数学运算，针对这些问题，朱伯芳[11]提出了既与试验资料吻合得较好，又便于数学运算的组合指数式。由于堆石坝的流变变化规律与混凝土热学力学性能变化规律具有一定的相似性，为此，本文从唯象角度建议一种组合指数型流变模型来反映堆石坝流变变形规律。

2 堆石坝流变分析

2.1 堆石坝的组合指数型流变模型

由于3 参数、6 参数和7 参数指数流变模型等均仅有一个指数式进行流变收敛率调节，难以同时合理地反映蓄水初期和蓄水后期的沉降变化规律，为此，采用组合指数式将堆石坝流变变形规律表示如下

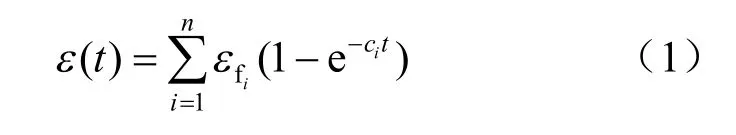
相应的应变速率为

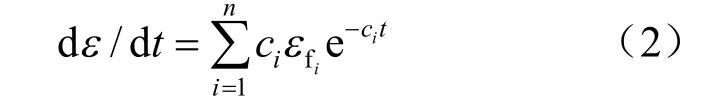
式中：ε为随时间增长的应变；t为时间；εfi和 ci均为参数；n为组合项数；e-cit为以常数e为底的指数函数；相当于t→∞时的最终流变量。

由实测资料表明，堆石坝的变形大都在建成若干年后逐渐沉降稳定。经验表明[11]，组合指数式右边只需取2 项，即可较好地反映堆石坝流变变形规律。以下对2 个指数式累加的组合指数型流变模型进行阐述。

最终流变量εf1+εf2与应力状态有关。对于堆石料而言，其体积流变和剪切流变有不同的规律。参照沈珠江等[1]试验研究结果，对体积与剪切流变分别采用如下关系式：

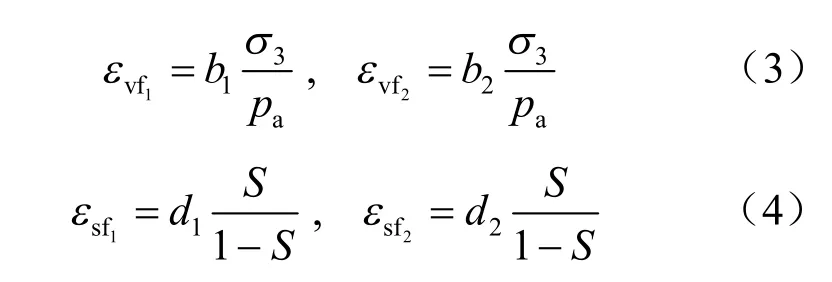
式中：b1、b2、d1、d2为参数；εvf1、εvf2分别为第1项和第2 项最终体积流变量；εsf1、εsf2分别为第1项和第2 项最终剪切流变量；b1+b2相当于σ3=pa时最终体积流变量；d1+d2为应力水平S=0.5时的最终剪切流变量，破坏时S=1.0，εsf1→∞，εsf2→∞。计算时如S ≥ 1.0，可限定S=0.95。

值得注意的是，对于高围压条件下，可对式（3）和式（4）的εvf2和 εsf2进行修正，以反映高围压下非线性增大。

假定堆石料的体积流变与剪切流变都可用式（2）描述，由式（2）得体积变形和剪切变形速率为

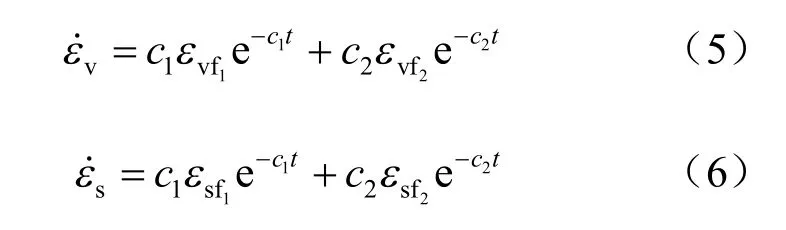
显然，当 c1=c2=c时，式（5）、（6）可以退化为3 参数指数型流变模型。

假设塑性势函数为Mises 屈服函数，采用Prandtl-Reuss 流动法则，应变张量的流变速率可以写为[12]

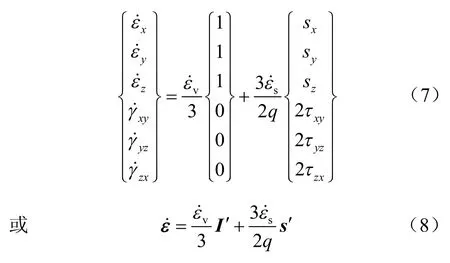
2.2 组合指数型流变增量分析

面板堆石坝的施工是分层填筑，蓄水过程是逐渐完成的。因此，在面板堆石坝的不同施工及蓄水阶段，不同单元的流变时间不同。采用统一时间，将使时间的记录过程复杂化，为此，对时间的计算技术进行改造，采用相对时间[1]进行流变分析。

将式（5）、（6）相应改写为

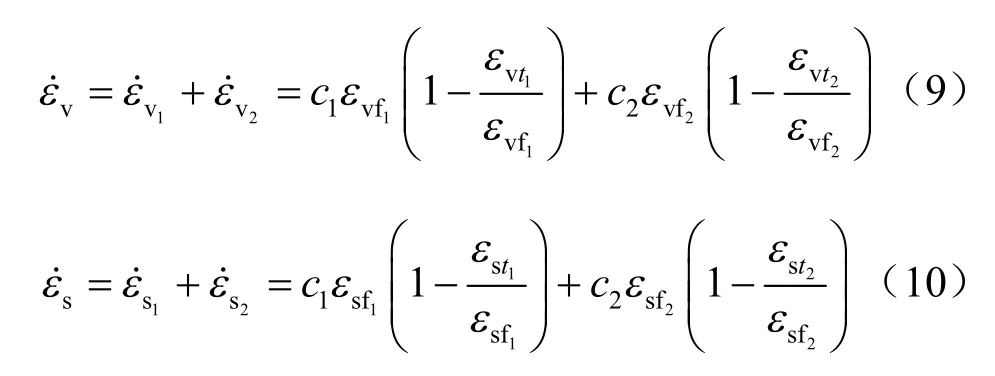
式中：εvt1、εvt2、εst1和εst2分别为t 时刻2 项指数式已累积的体积和剪切变形。其可以用下式计算：

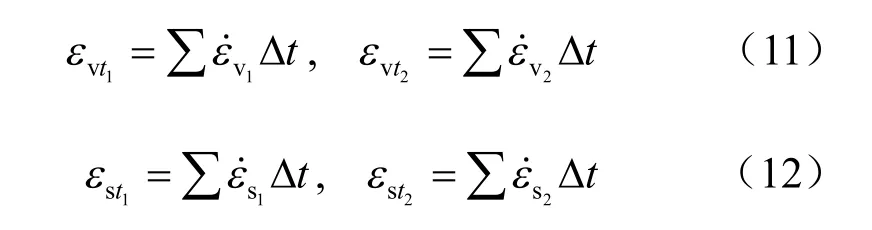
相应 Δt 时段内的体积和剪切流变应变增量为

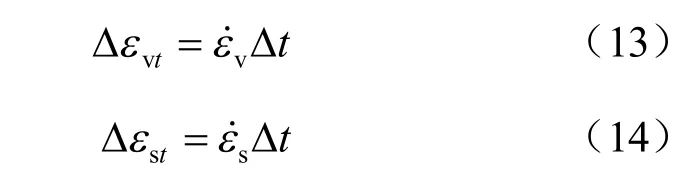
应变分量的流变增量可以写为[12]

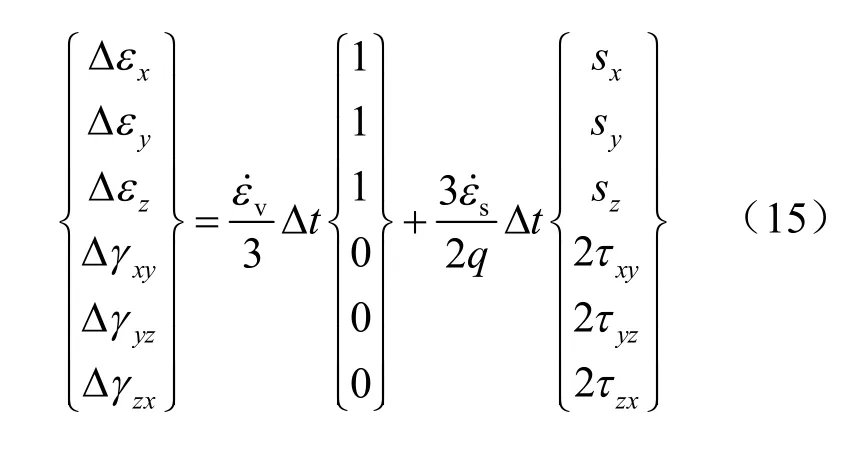
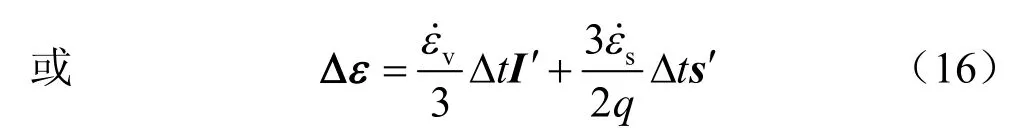
2.3 堆石体组合指数型流变分析步骤

采用有限单元法进行堆石体流变分析的计算步骤如下[1-2]

Step1：根据施工及蓄水过程，采用中点增量法对相应荷载级先采用邓肯E-B 模型计算瞬时变形，得到本级末的单元应力及应力水平。

Step2：根据施工进度安排，确定该级加荷所经历的时间Ti，将该段时间分为若干时段Δt 。

Step3：假定该 Δt 时段内应力不变，按式（3）、（4）计算对应的剪切流变 εsf和体积流变 εvf。用式（9）、（10）计算应变速率，用式（11）、（12）计算累积流变量，用式（16）得到相应流变增量。

Step4：按初应变法进行有限元分析，得到相应的位移增量、应力增量，累积得到总位移、总应力。

Step5：对加荷时段时间进行判断，如该加荷级时间结束，则回到Step1 循环，否则回到Step3 循环。

本文采用Visual Fortran编制了面板堆石坝流变分析程序。

3 实例分析

华中地区某面板堆石坝，设计最大坝高为114 m，顶宽为10 m，坝顶长为328 m，面板堆石坝上、下游坝坡均为1:1.4，上游设钢筋混凝土防渗面板，厚度为30～68 cm，其后分别为垫层、过渡层、新鲜岩石区（上游堆石区）、弱风化岩石区（下游堆石区），堆石料以灰岩料为主。本文采用组合指数型流变模型分析该面板堆石坝的流变变形特性。

3.1 三维非线性有限元计算模型

（1）有限元计算模型

图1 面板堆石坝三维整体有限元模型(坝体部分)Fig.1 Three-dimensional finite element model of concrete faced rockfill dam(dam section)

对该面板堆石坝建立三维整体有限元模型，如图1 所示，坝体共剖分7 817 个单元，8 556 个节点；其中，主堆石体单元4 003 个，次堆石体单元1 254个，面板单元604 个，接触面单元和垫层单元1 956个。

（2）邓肯E-B 模型参数

本文采用工程上使用较广泛的邓肯E-B 模型分析该堆石体应力-应变非线性关系。该堆石坝以灰岩料为主，主堆石和次堆石的邓肯E-B 参数采用工程类比法的反演参数，垫层料和过渡料采用室内试验值，见表1。表中，0φ为围压为一个大气压时的内摩擦角，φΔ为随压力变化的内摩擦角，Rf为破坏比，K为切线模量系数，n为切线模量指数，Kb为体积模量系数，m为体积模量指数。

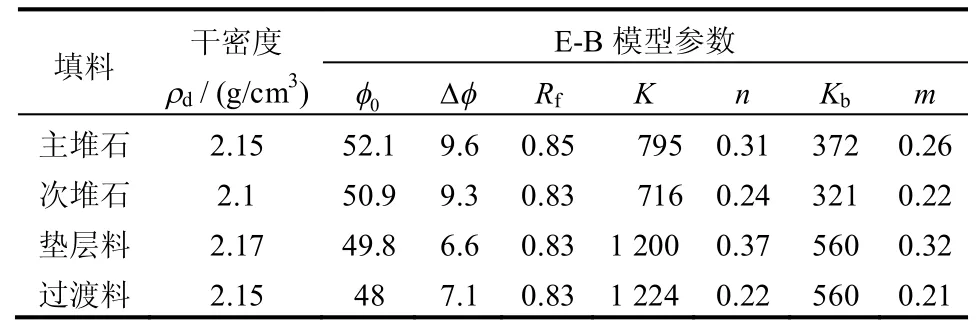
表1 邓肯E-B 模型计算参数表Table 1 Calculating parameters of Duncan E-B model

（3）组合指数型流变模型计算参数

由于没有试验流变参数和足够的现场监测位移，针对该堆石坝以灰岩料为主，首先参考文献 [1-2]的3 参数指数流变模型确定堆石料的流变参数初始值；由于文献[1]基于实测位移反馈流变参数时，三维流变应变增量计算式为，对比式（15）可见，剪应力对应的流变应变增量相差3 倍，因此，相对文献[1-2]给出的流变参数值，流变参数d 除以了3；然后采用工程类比法反演的主堆石流变参数为b=0.000 4、c=0.002 6、d=0.001 5，次堆石的流变参数为b=0.000 6、c=0.003 6、d=0.00 2。

由于3 参数指数流变模型难以同时合理地反映蓄水初期和蓄水后期的沉降变化规律，为此，采用组合指数型流变模型进行堆石体的流变分析。经试算，b1和d1分别取0.6 倍3 参数指数流变模型的b值，b2和d2分别取0.4 倍3 参数指数流变模型的d值；c1取3 参数指数流变模型的c 值，敏感性分析c2取β 倍3 参数指数流变模型的c 值，以对比不同c2下堆石坝的流变特性，其中，β 分别取1.0、0.8、0.5、0.2，见表2。由式（5）、（6）可见，当 c2=c1时，组合指数流变模型退化为3 参数指数流变模型。

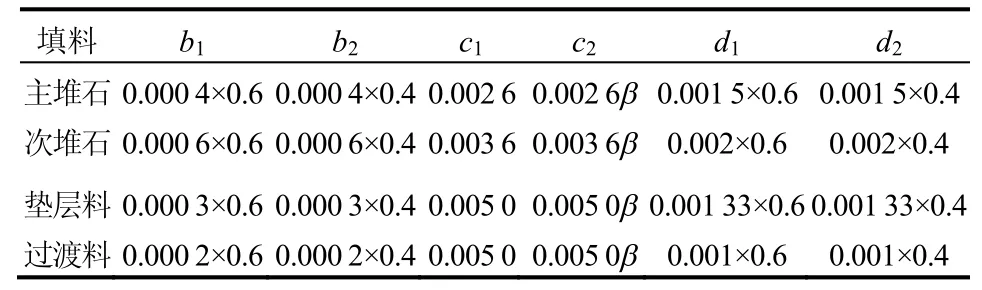
表2 三参数流变模型计算参数表Table 2 Calculating parameters of rheological model of 3 parameters

（4）计算加荷分级

根据该面板堆石坝设计施工关键线路并略做调整，分级加荷次序示意见表3 和图2，蓄水至正常高水位后，再仿真计算近8 a。

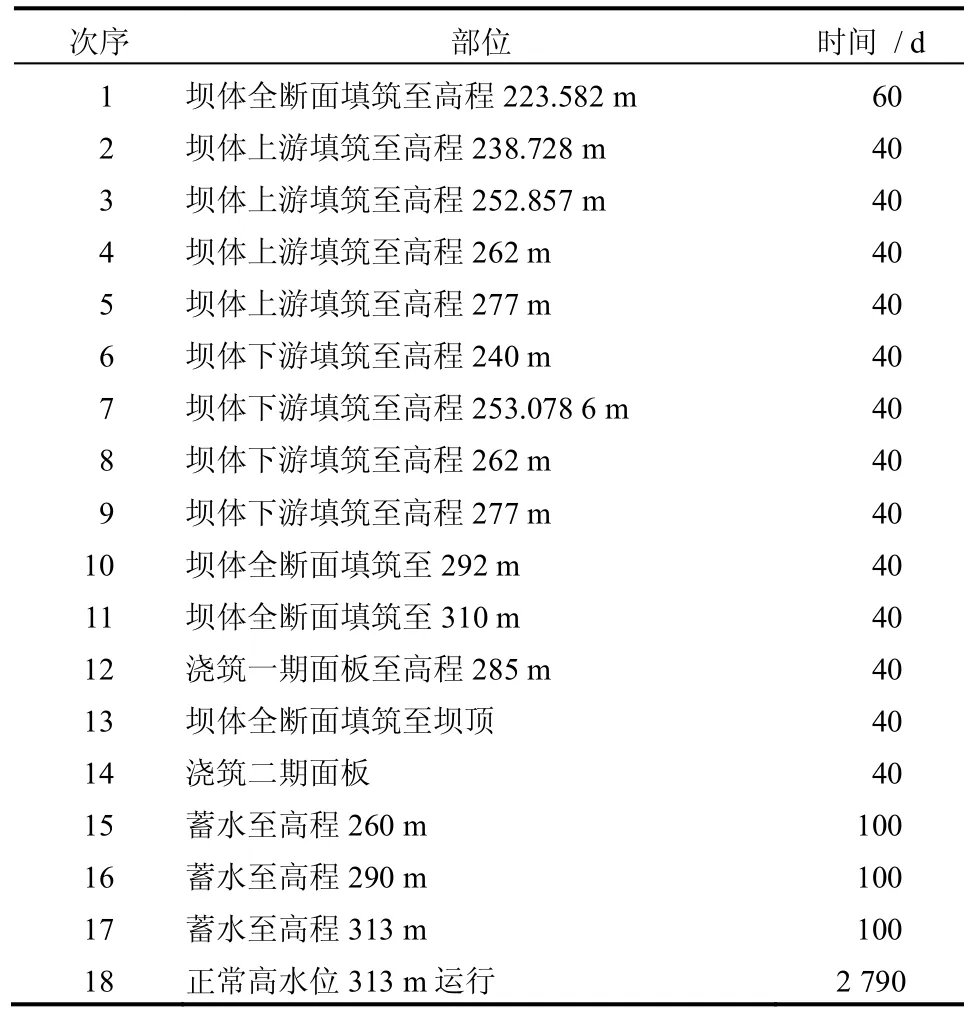
表3 分级施工进度表Table 3 Stage construction schedule

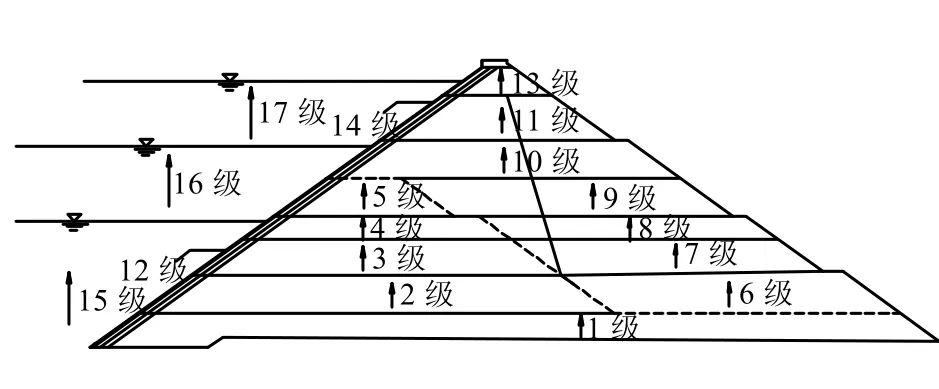
图2 分级加荷示意Fig.2 Stage construction loading sketch

3.2 堆石坝流变变形特性对比

当 c2=c1时，采用组合指数型流变模型计算的面板堆石坝在竣工、蓄水至正常高水位以及运行3 a后堆石体的变形如图3 所示，图中位移等值线单位为m，蓄水至正常高水位后，不同 c2取值下坝顶沉降增量过程线和EL277典型测点沉降增量过程线如图4 所示。

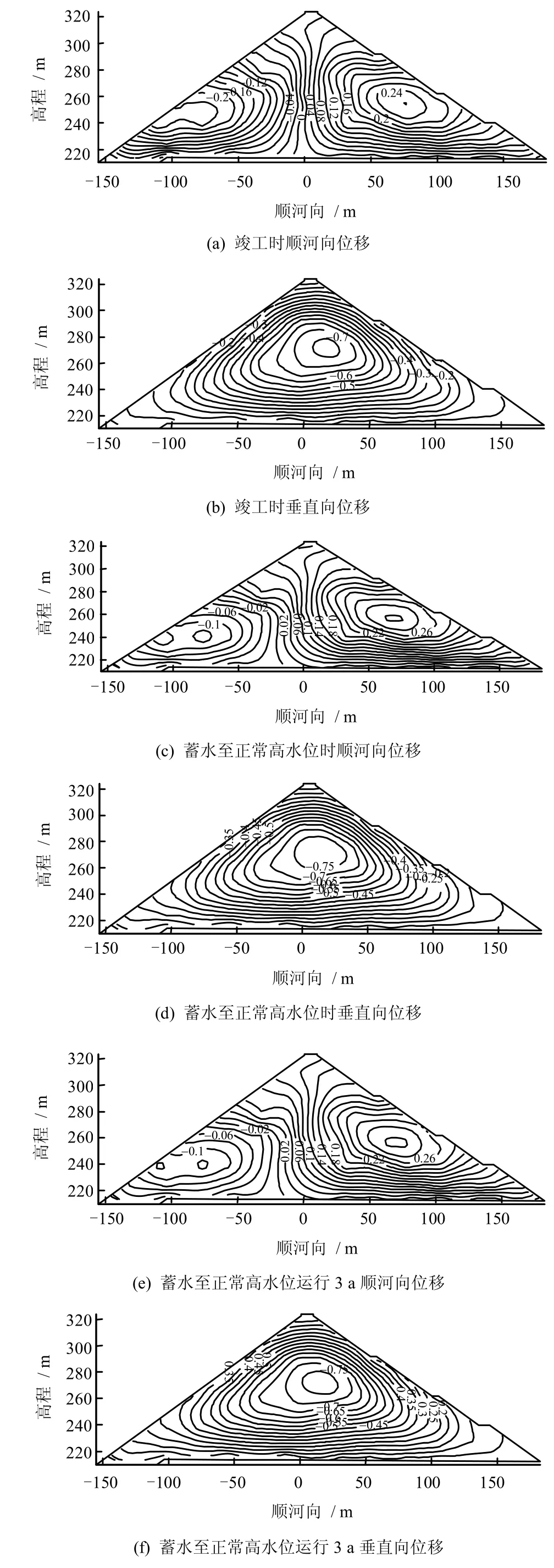
图3 典型时刻堆石体变形(单位:m)Fig.3 Deformations of rockfill dam in typical time

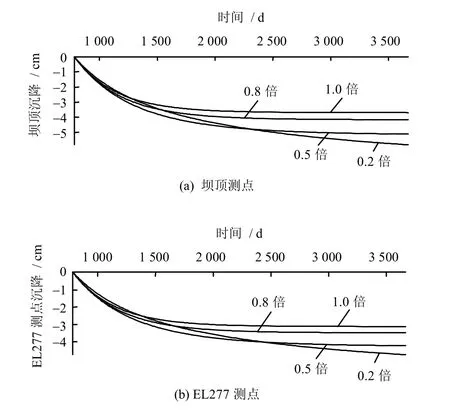
图4 蓄水至正常高水位后不同c2取值下增量沉降过程线Fig.4 Increment sedimentation process line in different values of c2after water storage to normal high water level

由计算可见：

（1）当 c2=c1时，该面板堆石坝竣工时，堆石体最大沉降为76.01 cm，向上游最大水平向位移为-23.47 cm，蓄水至正常高水位时，堆石体最大沉降为79.16 cm，向上游最大水平向位移为-13.37 cm，蓄水运行3 a 时，堆石体变形渐趋稳定，最大沉降为82.13 cm，向上游最大水平向位移为-12.68 cm。蓄水至正常高水位时，最大面板挠度为19.103 cm，蓄水运行3 a 时，最大面板挠度增大到20.661 cm。面板最大挠度与堆石坝施工期最大沉降的比值约为0.25，这与Montanez Cartaxo 等的结论是一致的[10]。

（2）采用组合指数型流变模型进行流变分析时，该面板堆石坝蓄水至正常高水位后，不同c2取值引起堆石坝的增量沉降和沉降变化率不一样，例如，c2分别取0.2、0.5、0.8、1.0 倍的c1时，蓄水运行5 a 时，坝顶沉降速率分别为3.455，1.329，0.442，0.257 mm/a。随着c2取值的减小，堆石坝需要更长的流变时间才能趋于稳定。由式（5）、（6）可见，当 c2=c1时，组合指数流变模型退化为3 参数指数流变模型，即相对于一个指数式的流变模型而言，采用组合指数型流变模型可以更好地反映蓄水初期和后期堆石坝的流变变形特性。对比谢腊德、库克等[10]对碾压堆石面板坝开始蓄水后坝顶沉降量的统计分析，当c2取0.2 倍的c1时，在蓄水5 a后，碾压堆石坝沉降率约为3.5 mm/a。

（3）由图4 的计算可见，由于堆石料最终的流变量与应力状态有关，虽然本文采用的组合指数型流变模型的b1和d1分别取0.6 倍3 参数指数流变模型的b 值，b2和d2分别取0.4 倍3 参数指数流变模型的d 值，由于增量计算过程反映了材料的非线性特性，仅调整c2的取值，但计算的堆石坝变形不具有线性叠加性。例如，c2分别取0.2、0.5、0.8、1.0倍的c1时，蓄水运行8 a 后，坝顶增量沉降分别为5.840、5.128、4.161、3.697 cm，c2取0.2 倍和0.5倍c1的坝顶增量沉降较c2取1.0 倍c1的坝顶增量沉降大，但c2取1.0 倍c1的坝顶增量沉降过程线渐趋稳定，而c2取0.2 倍和0.5 倍的c1的坝顶增量沉降过程线尚未稳定。注意到当 c2=c1时，组合指数流变模型退化为3 参数指数流变模型，即仅有一个指数式流变模型难以同时合理地反映蓄水初期和后期的沉降变化规律。

4 结 论

（1）组合指数式流变模型由于具有2 个及以上指数式协调调整堆石坝的变形和变形变化率，可较好地反映堆石坝流变变形规律且数学运算方便。

（2）由于堆石料最终的流变量与应力状态有关，增量计算过程反映了材料的非线性特性，仅调整c2的取值，但计算的堆石坝变形不具有线性叠加性。

（3）组合指数式流变模型适用于基于实测变形进行堆石坝流变变形反馈，但组合指数式流变模型的力学机制还有待进一步研究。

[1]沈珠江,赵魁芝.堆石坝流变变形的反馈分析[J].水利学报,1998,29(6):1－6 SHEN Zhu-jiang,ZHAO Kui-zhi.Back analysis of creep deformation of rockfill dams[J].Journal of Hydraulic Engineering,1998,29(6):1－6.

[2]郭兴文,王德信,蔡新,等.混凝土面板堆石坝流变分析[J].水利学报,1999,30(11):42－47.GUO Xing-wen,WANG De-xin,CAI Xin,et al.Rheological analysis of concrete faced rock-fill dam[J].Journal of Hydraulic Engineering,1999,30(11):42－47.

[3]米占宽,沈珠江,李国英.高面板堆石坝坝体流变性状[J].水利水运工程学报,2002,(2):35－41.MI Zhan-kuan,SHEN Zhu-jiang,LI Guo-ying.Creep model for high concrete face rockfill dams[J].Hydro-science and Engineering,2002,(2):35－41.

[4]李国英,米占宽,傅华,等.混凝土面板堆石坝堆石料流变特性试验研究[J].岩土力学,2004,25(11):1712－1716.LI Guo-ying,MI Zhan-kuan,FU Hua,et al.Experimental studies on rheological behaviors for rockfills in concrete faced rockfill dam[J].Rock and Soil Mechanics,2004 25(11):1712－1716.

[5]方维凤.混凝土面板堆石坝流变研究[D].南京：河海大学,2003.FANG Wei-feng.Research on creep of concrete face rockfill dam[D].Nanjing:Hohai University,2003.

[6]程展林,丁红顺.堆石料蠕变特性试验研究[J].岩土工程学报,2004,26(4):473－476.CHENG Zhan-lin,DING Hong-shun.Creep test for rockfill[J].Chinese Journal of Geotechnical Engineering,2004,26(4):473－476.

[7]周伟,常晓林,曹艳辉.堆石体流变对分期浇筑的面板变形影响研究[J].岩石力学与工程学报,2006,25(5):1043－1048.ZHOU Wei,CHANG Xiao-lin,CAO Yan-hui.Study of influence of rockfill rheology on face deformation with substage construction[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(5):1043－1048.

[8]沈凤生,陈慧远,潘家铮.混凝土面板堆石坝的蓄水变形分析[J].岩土工程学报,1990,12(1):73－81.SHEN Feng-sheng,CHEN Hui-yuan,PAN Jia-zheng.Deformation analysis of CFRD in water storage period[J].Chinese Journal of Geotechnical Engineering,1990 12(1):73－81.

[9]蔡新,成峰,杨建贵,等.土石坝流变非线性分析[J].河海大学学报,1999,27(6):20－24.CAI Xin,CHENG Feng,YANG Jian-gui,et al.Rheological analysis of earth-rock dams[J].Journal of Hohai University,1999,27(6):20－24.

[10]曹克明,汪易森,徐建军,等.混凝土面板堆石坝[M].北京:中国水利水电出版社,2008.CAO Ke-ming,WANG Yi-sen,XU Jian-jun,et al.Concrete face rockfill dam[M].Beijing:China Water Power Press 2008.

[11]朱伯芳.混凝土热学力学性能随龄期变化的组合指数公式[J].水利学报,2011,42(1):1－7.ZHU Bo-fang.Compound exponential formula for variation of thermal and mechanical properties with age of concrete[J].Journal of Hydraulic Engineering,2011 42(1):1－7.

[12]黄耀英,沈振中,郑宏,等.关于堆石料三维流变速率的一点注记[J].岩土力学,2014,35(6):1569－1571,1592.HUANG Yao-ying,SHEN Zhen-zhong,ZHENG Hong,et al.Note on three-dimensional rheological rate of rockfill material[J].Rock and Soil Mechanics,2014 35(6):1569－1571,1592.