基于Steiner点的移动传感网络汇聚节点选址

2015-02-16梁久祯李军飞

西北大学学报（自然科学版） 2015年2期

关键词：偏心顶点节点

梁久祯，李军飞

(江南大学物联网工程学院,江苏无锡 214122)

·信息科学·

基于Steiner点的移动传感网络汇聚节点选址

梁久祯，李军飞

(江南大学物联网工程学院,江苏无锡 214122)

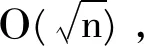
汇聚节点;移动传感网络;Steiner中心;结构意识自适应

无线传感器网络(WSN)是一个非常有前景的技术,有着广阔的应用潜力,如战场监视、事件检测、敌情监视和动物行为发现等。随着无线通信和微系统技术进步,使得各种低功耗和低成本效益的传感器平台广泛地应用在军事、民用、医疗等领域,旨在让人们更好地与物理世界沟通。

近几年,移动传感网络(mWSNs)应用和研究越来越广泛。像水下传感网络[1],节点都是伴随水流、潮汐不停地发生位置移动,文献[2]研究野生斑马生活习性,根据斑马生活运动习性将斑马网络(ZebraNet)分为放牧,放牧行走和快速奔跑三层移动模型;斑马网络和水下网络的拓扑结构时刻都在发生变化,这种群体移动网络都需要有动态实时的汇聚选址策略来满足网络动态变化。

目前,国内外学者对汇聚节点的选址的研究中做了一定的工作。文献[3]使用蚁群路由算法,在面向寿命的策略上实现了网络寿命的大幅提高; 文献[4]提出了4种汇聚节点移动模式,通过充分利用汇聚节点的移动特征来实现数据包高效分发,将任务转移到能量多的汇聚节点处提升网络性能。可以看出目前绝大多数算法是基于静态的网络或缺乏自适应能力。

在无线传感网络中,边缘检测常用来发现目标是非常有效的。文献[5]设计了结构意识自适应算法(SASA),通过在井下天顶上均匀部署传感器节点,当塌方发生时,塌方会带走部分节点,塌方边缘的节点会形成一个凸多边形结构,从而来预报塌方的大小和具体位置。文献[6]提出了一种本地事件边界检测算法,实现了错误节点有效检测。以上表明边结构是群体网络的一个非常有价值的特征。

针对以上问题,本文提出了一种在移动传感网络中使用Steiner点作为汇聚节点位置的SCSN模型,该模型是基于边结构的设计,并结合增强型自意识自适应算法(ASASA);能够适用于群体特征的移动传感器网络。解决了移动网络汇聚节点选址难问题。

1 SCSN系统模型

SCSN主要是针对一个拥有大规模传感器节点的移动传感器网络,如图1,所有的节点整体以一个结构不断变化的凸多边形群体以非直线的轨迹发生移动;网络采用单个可移动中心汇聚节点,负责全网感知数据的汇聚外,还要负责SCSN移动网络边结构的构造和动态维护。传感器节点的定位都采用被动定位,像安装GPS模块或是基于锚节点的定位算法,节点每次SCSN更新负责上传自己新的位置信息。

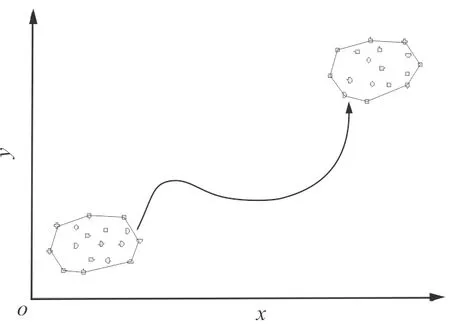
图1 群居野生斑马活动的移动网络实例Fig.1 Mobile network of wild zebra

SCSN模型网络节点分为中心汇聚节点、边节点和内部节点(如图2)。

1.1 SCSN算法

SCSN算法运行在中心汇聚节点,主要负责算法的具体实现,伪代码算法如下。

1. Absolute position convert to relative position

2. if initialed == false

3.S=E; initialed = true(Erepresent all nodes)

4. end if

5. broadcast request As for Convex nodesSposition

6. do receive packagesPS

while all requested nodes′ positon received

7. Construct new convex polygonS

8. BroadcastS

9. # calculate the steiner pointP

10.P= Steiner(S)

11. Sink node move toP

12. sleep (T)

13. Continue

系统初始化时,设置凸顶点集合S为所有节点集E(S=E)(第2-3行),凸壳重构周期为T。SCSN系统每一周期更新时,首先汇聚节点广播请求边节点凸集S返回当前位置数据(第5行),边节点收到广播后,通过自身定位模块计算自己当前位置并将最新的位置信息上传给汇聚节点; 汇聚节点收到所有请求边节点的位置数据包时(第6行),构造出网络的凸多边形顶点新集合S(第7行),如图3(t1),然后广播边结构顶点集合S(第8行);普通节点收到广播后,保存当前网络边结构顶点集合S位置信息,如发现自己坐标Pi∈S,就将自己设置为边节点(图2深色点);这时每个节点都有最新网络凸多边形的位置信息;同时汇聚节点计算出新的Steiner中心P(第10行,图2五角星),并移动到新P处(第11行)。

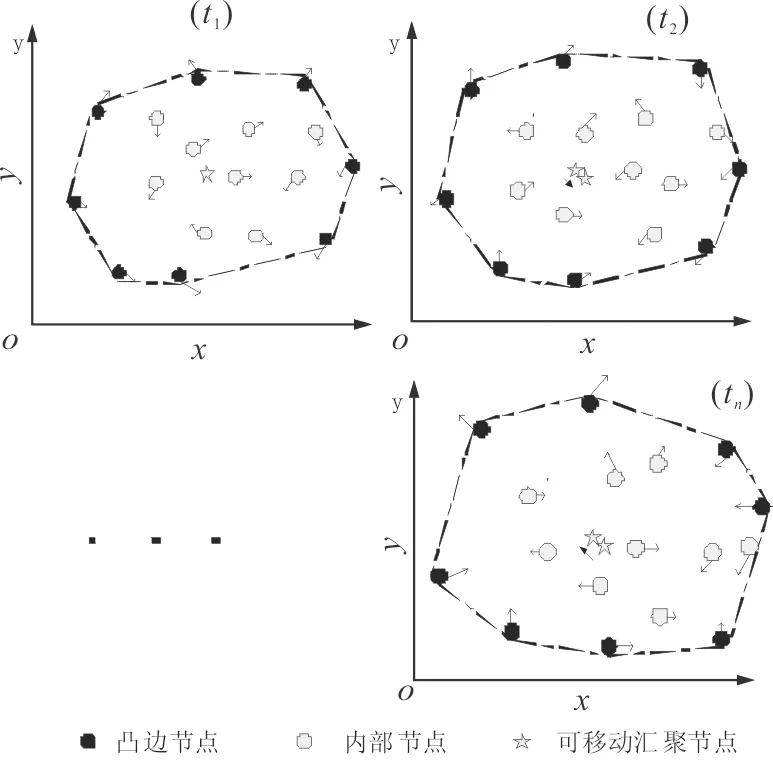
图2 连续时间凸壳的动态更新Fig.2 Convex hull dynamic updates continuously

在移动网络中,图2分别表示连续时刻t1,t2,…,tn网络节点移动拓扑结构图,节点的自由移动使得移动网络拓扑结构不断发生变化,Steiner中心需要实时的更新边结构才能满足实际的需求。在每个重构周期T到达后(第12行),汇聚节点广播请求所有边节点Pi(Pi∈S)位置数据包As(第5行),重复步骤(5-12),周期性的更新凸结构和Steiner中心P,让汇聚节点实时的保持在Steiner中心位置,如图2汇聚节点不断的移动到新的位置。图3表示移动网络在连续变化时间内,通过周期性的更新凸壳来保持汇聚节点在Steiner中心处的SCSN系统模型图。

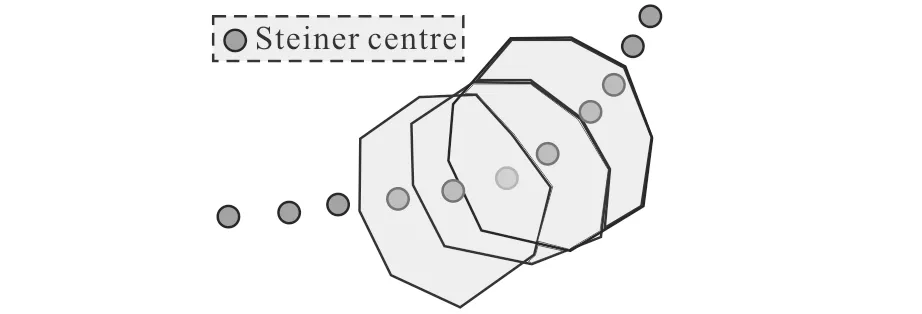
图3 SCSN系统模型变化图Fig.3 SCSN model

1.2 ASASA算法

ASASA(Advanced Structure-Aware self-adaptive)是一种基于边界意识自适应的算法。SCSN算法在周期性的更新边结构时,每次只请求凸壳顶点节点集合S的位置信息,无法判断内部节点是否移出凸壳。如图5节点A,需要A自身意思判断和上报违规情况。按破换边结构类型分为以下3种情况,如图4。

Case 1 凸壳边节点移动到内部节点以内(图4a);

Case 2 内部节点移动到凸壳以外(图4b);

Case 3 边节点向内和内部节点向外移动(图4c)。

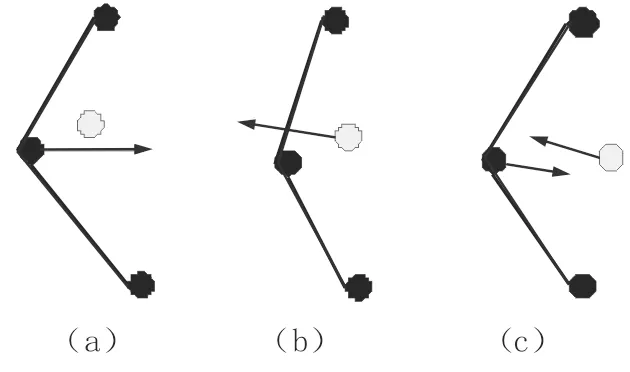
图4 3种凸壳变换违规情况Fig.4 Three cases of violations

以上都会造成边结构受到非顶点节点的破坏,但是，SCSN算法汇聚节点自身只能获取顶点集合的位置信息,无法判断非顶点节点的位置是否越界。不会将外围非顶点节点添加到顶点集合S中。为了维护正确的边结构,设计了增强型结构意识自适应(ASASA)算法来解决以上问题。

ASASA算法实现:

第一步内部节点Pi接收最新广播凸顶点集S。

第二步比较自己位置Pi和S的关系,如果Pi(图4A点)发现自身的相对位置移动到了凸壳的外部(Pi∉Vs),意识到自己破坏了现有的边结构,为了适应SCSN边结构算法,Pi就向汇聚节点发送自己的新位置并请求添加到顶点集合S中。

第三步汇聚节点接收到破坏边界的请求后,将请求节点Pi添加到集合S中,重新构造凸壳。

第四步广播新凸顶点集S。

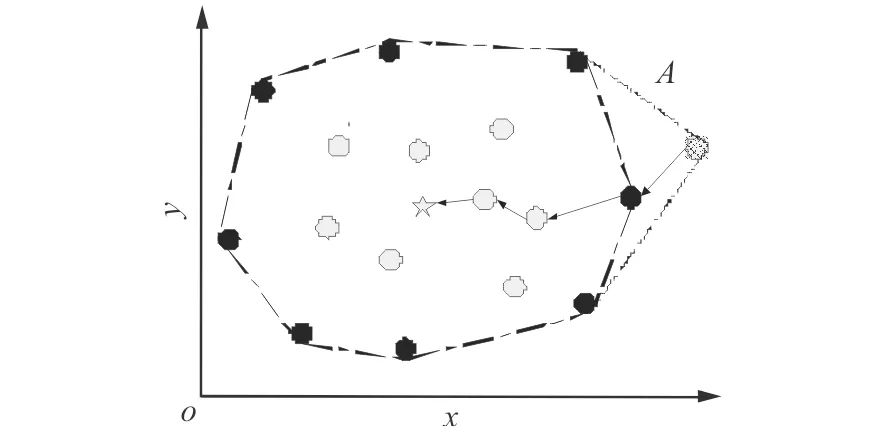
图5 违规节点请求重构凸壳Fig.5 Violated node request reconstruct new convex hull

在运行网络有节点破坏边结构情况下,通过以上步骤就可以将3种违规情况边结构及时纠正过来了,恢复SCSN系统的正常运行。以上只需内部节点的自意识来实现凸多边形边结构的动态维护。平时内部节点的任意移动都不会影响到SCSN。SCSN和ASASA的结合使得网络只需周期性获取凸顶点节点Pi(其中Pi∈S)位置信息就可以动态维护好整个网络结构及汇聚节点位置。

2 Steiner移动应用高稳定低偏心性

定义 1[8]设P是空间Rn上的d-维的凸多面体,那么Steiner点的函数离散定义

(1)

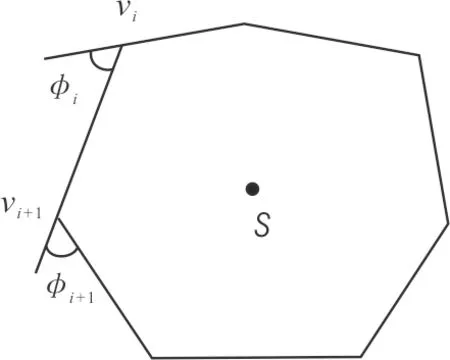
图6 Steiner点的几何定义Fig.6 Definition of Steiner

表1 R2上中心函数的对比[7]Tab.1 Compared different centre functions in R2

文献[7]中Durocher 在题目中指出Steiner中心在移动应用中具有高稳定和低偏心的特征。文中强调偏心性和稳定性是一个相对的性质,偏心性越小稳定性越强,反之亦然。表1是Durocher通过理论推导得出Steiner中心和其他4种函数中心的λ-偏心性和k-稳定性值。Durocher强调λ-偏心性值越小表示偏心性越低,k-稳定性值越大表示稳定性越高,Steiner的k-稳定性为0.785 4、λ-偏心性为1.115 3。通过表中数据对比可以看出, Steiner中心相比其他中心有低偏心性和高稳定性的优势。低偏心可使汇聚节点位置周期更新的中心位置移动的偏移量较小;高稳定可使中心每次更新移动距离稳定,不会出现忽远忽近。这对提升移动网络的整体性能来说是非常关键的。

3 性能分析与评价

无线传感器网络是一门综合性非常强的技术,作为物联网的感知神经末梢,对物理世界感知数据,其部署环境恶劣、能量和传输距离有限、应用场景复杂多样,对网络性能多方面提出严格的要求。参照移动传感器网络运行特点,做出以下部分性能对比分析。

3.1 动态自适应

移动传感器网络中节点的自由移动对算法的动态实时性提出了非常高的要求,节点的移动使得下一时刻网络的整体拓扑结构和路由链路发生改变,基于位置或者链路信息的算法需重新获取整个网络的结构才能重新计算新位置。传统的算法缺乏动态自适应和自意识,一旦网络结构发生变化,算法就失效了。

从图3SCSN的运动的模型可以看出。SCSN通过周期性的更新顶点节点位置信息表来维护实时的网络边结构和维持汇聚节点在Steiner中心处。并结合ASASA算法,使用边界意识来动态维护好整个网络的凸多边形结构,顶点的添加和删除都能够通过ASASA及时的修正过来。动态变化的网络始终保障汇聚节点在整个过程中动态实时的处于Steiner处。以上可以看出SCSN具有非常好的动态自意识、自适应能力。

3.2 低时延

文献[10],Akkaya等人认为时延在实时性的应用场景中(如军事检测、野生动物发现、目标跟踪)是一个非常关键的指标,并定义时延和边界节点到汇聚节点的最大跳数(K-hops)有关。移动网络对数据的实时性要求是非常高的,数据传输中的每经过一跳需要消耗上百毫秒的时间,跳数(K)越小实时性越高。

图7是随机测试的一个不均匀传感器网络,其中节点最大传输半径为15m,,测试比较了Steiner中心、最小距离和文献[3]的基于寿命算法选取汇聚节点位置时K-hops的值,根据文献[3]算法的能量公式和距离的平方相关,中心位置偏向密集一方。图8显示测试网络不同跳数内的节点所占的百分比。可以发现基于Steiner算法在A点时(K=5)所有节点都可以到达汇聚节点,同样从B，C两点是最小距离和和基于寿命算法的K值点分别为K=7，K=6。从图7各中心点的位置和图8对比实验分析可以得到,最小距离和和Chen算法有偏向密集一边,使得中心偏密集一方,从而稀疏一侧的跳数会加大。Steiner中心处于凸多边形的区域中心,使得中心到凸壳的边距离比较平均,降低了网络最大传输距离，从而减少网络的最大跳数,加快网络收敛速度。

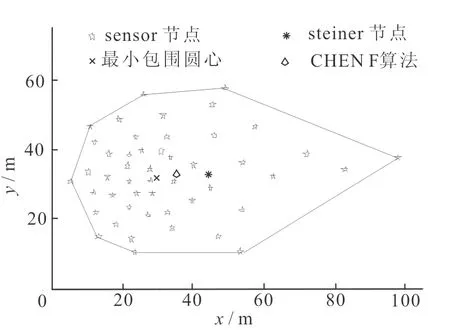
图7 随机不均匀网络节点分布图Fig.7 A test case of random distribution network

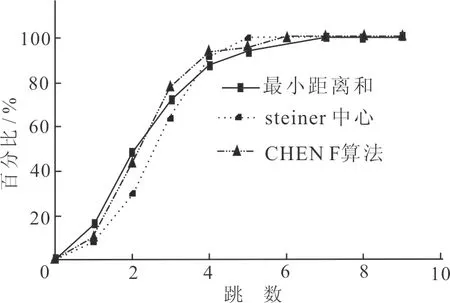
图8 K-hops节点所占的百分比Fig.8 The percentage of K-hops nodes

3.3 低复杂度

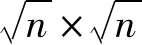
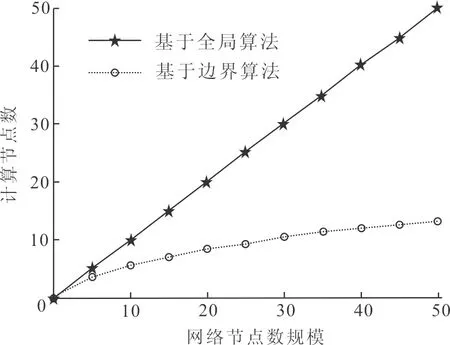
图9 节点个数复杂度Fig.9 Complexity of the number of nodes

3.4 强鲁棒性

图10为在100个节点的测试网络中,算法在一次更新汇聚节点位置时,离汇聚节点不同跳数(K-hops)节点的平均转发包的个数。从图中很容易发现基于全局的算法获取所有节点位置请求后,越靠近汇聚节点,转发数据包的个数越多,网络的负载越重,会造成网络拥塞、延时甚至网络的瘫痪,给网络的运行带来极大的挑战。SCSN基于边结构的算法,每次只要求获取凸壳顶点位置信息,减少了占绝对大数的内部节点数据包,对汇聚节点及其邻近的节点来说,传输数据包的个数大大地减少,比较发现基于边结构的算法鲁棒性明显优于基于全局的算法。

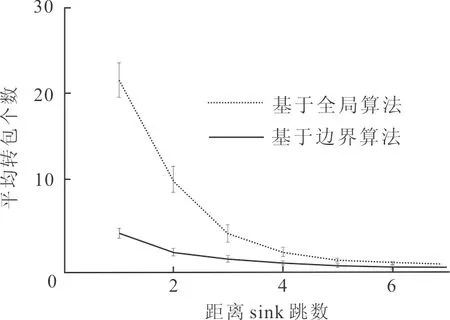
图10 不同跳数节点平均转发包个数Fig.10 Average forwarding packets of different hops

4 实验

在这部分内容中,我们使用Matlab-2011b仿真工具。实验对比了凸多边形的Steiner中心、质心、欧几里得和最小包围圆4个几何函数中心,分别对比在移动网络的连续更新周期内中心位置的偏移量来验证SCSN使用Steiner中心作为汇聚节点是否具有高稳定低偏心的性质。仿真参数如表2。

表2 仿真参数Tab.2 Simulation parameters

图11 偏移量随时间分布图Fig.11 Distribution of offset

图11显示了在移动变化的网络中,实验了4种不同函数中心在连续的20个更新周期内汇聚节点位置的偏心量。通过图可以发现最小包围圆圆心构成的3个点任意小的移动都会造成非常大的中心偏移。说明圆心的偏移量是非常大而且是极不稳定的;欧几里得中心的λ-偏心性为1，k-稳定性为0;在正常的情况下,它的更新偏移量都小于1m,表明其偏心性非常小。但是，在T=5，10，16时刻,由于SCSN的ASASA算法检测到凸壳有边节点的加入或删除,造成非常大的偏移,说明在有边节点加入或删除的情况下,欧几里得中心是不稳定的。质心的λ-偏心性为2，k-稳定性为1,图中显示其有非常好的稳定性,但偏心量要比Steiner大。Steiner中心的k-稳定性为0.785 4，λ-偏心性为1.115 3。图表显示正常情况下Steiner中心的周期更新偏移量要比质心小,比欧几里得要大。但是，在有边节点加入和移除时,Steiner中心要比欧几里得中心稳定得多。由此可得出结论,Steiner中心相比其他凸多边形中心作为移动传感器网络汇聚节点位置具有高稳定和低偏心的特性。

5 结语

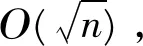
[1] 吕超, 王硕, 谭民. 水下移动无线传感器网络研究综述[J]. 控制与决策, 2009, 24(6): 801-807.

[2] JUANG P, OKI H, WANG Y, et al. Energy-efficient computing for wildlife tracking: Design tradeoffs and early experiences with ZebraNet[C]//ACM Sigplan Notices. ACM, 2002, 37(10): 96-107.

[3] CHEN F, LI R. Sink Node Placement Strategies for Wireless Sensor Networks[J]. Wireless personal communications, 2013, 68(2): 303-319.

[4] CHATZIGIANNAKIS I, KINALIS A, NIKOLETSEAS S. Efficient data propagation strategies in wireless sensor networks using a single mobile sink[J]. Computer Communications, 2008, 31(5): 896-914.

[5] LI M, LIU Y. Underground structure monitoring with wireless sensor networks[J].ACM Transations on Sensor Networks, 2009,5(2):10-15.

[6] DING M, CHEN D, XING K, et al. Localized fault-tolerant event boundary detection in sensor networks[C]//INFOCOM 2005. 24th Annual Joint Conference of the IEEE Computer and Communications Societies, Miami:IEEE, 2005, 2: 902-913.

[7] DUROCHER S, KIRKPATRICK D. The Steiner centre of a set of points: Stability, eccentricity, and applications to mobile facility location[J]. International Journal of Computational Geometry & Applications, 2006, 16(04): 345-371.

[8] 王德江.支撑函数及其在图像特征表示中的应用[D].无锡:江南大学,2014,7

[9] NOWAK R, MITRA U. Boundary estimation in sensor networks: Theory and methods[C]//Information Processing in Sensor Networks. Berlin Heidelberg: Springer, 2003: 80-95.

[10] KIM D, WANG W, SOHAEE N, et al. Minimum data-latency-bound k-sink placement problem in wireless sensor networks[J]. IEEE/ACM Transactions on Networking (TON), 2011, 19(5): 1344-1353.

(编辑曹大刚)

Steiner centre as sink node position for mobile wireless sensor network

LIANG Jiu-zhen, LI Jun-fei

(School of Internet of Things,Jiangnan University, Wuxi 214122， China)