预腐蚀铝合金贯穿疲劳裂纹扩展行为的统一表征模型
2015-02-15李旭东穆志韬刘治国
李旭东,穆志韬,刘治国
(海军航空工程学院 青岛校区,青岛266041)
铝合金相对于先进复合材料的低成本优势使得其仍然是飞机中关键承力部件的主要材料。对于沿海机场服役的飞机结构,其铝合金构件既要承受高盐雾高温高湿大气的腐蚀损伤还要承受飞行过程中的交变疲劳载荷,会产生疲劳裂纹并导致承力结构承载能力下降,威胁飞行安全。飞机维护规程中都有对飞机承力结构件进行周期性检查的要求,确保构件无裂纹或者在扩展到容许极限之前能够将裂纹检测出来并进行维修[1-6]。定检周期过长可能会带来危险,定检周期过短又会增加过多的不必要的维护工作量。因此需要根据材料的疲劳扩展寿命合理确定合理的检验间隔,而这都依赖于合理有效的裂纹扩展速率模型[7-12]。
1 试验
以LD2铝合金为试验材料,沿着轧制方向加工成狗骨状平板试验件,其主要的化学成分为(质量分数/%):0.45%~0.9%Si;0.5%Fe;0.2%~0.6%Cu;0.15%~0.35%Mn;0.9%Mg;0.2%Zn;0.15%Ti;Al余量。主要力学性能:弹性模量54.485GPa,屈服强度255MPa,抗拉强度290MPa,延伸率8.9%,裂纹扩展门槛值ΔKeffth=2.59MPa·。试验件尺寸如图1所示。
预腐蚀试验按照文献[3]提供的我国南方某机场的等效加速腐蚀环境谱在ZJF-45G周期浸润环境试验箱中完成。腐蚀溶液为5%NaCl溶液加稀硫酸溶液混合成pH=4±0.2的溶液。在(40±0.2)℃,相对湿度(Relative humidity,缩写RH)90%~95%的空气中使用60W紫外线灯进行全程辐照。环境箱中每一次干-湿交变包括浸泡5min,烘烤12min。干湿交变348次循环,累计试验时间96h,等当量于服役环境中自然腐蚀1个日历年。本文中所用两批试件分别当量加速腐蚀到10a和20a。随后对预腐蚀试验件在酒精溶液中进行超声波清洗,去除表面的腐蚀产物便于观测裂纹的扩展,并利用科士达3300显微镜对预腐蚀后的试件表面进行拍照。在MTS810疲劳试验机上对未腐蚀、腐蚀10a、腐蚀20a的试件进行疲劳加载室温20℃,加载频率6Hz,正选波形,R=0.1,最大应力240MPa,加载过程中每隔1 000~10 000个应力循环将加载频率降低至0.5Hz,通过读数显微镜在100×放大倍率下根据显微镜自带的标尺读取裂纹张开时的长度,并记录其所对应的疲劳应力循环次数。每种试验件至少进行3个有效的平行试验。

图1 试件尺寸(单位:mm)Fig.1 Specimen dimension
2 结果与讨论
2.1 试验结果分析
将所得到的裂纹长度随循环次数的变化曲线进行差分,可以得到裂纹扩展速率。利用应力强度因子手册可以计算单边缺口试件的应力强度因子计算公式,如式(1)所示。

式中:Δσ为疲劳应力幅值;a表示裂纹的总长度,需要计入预制缺口的长度,即其数值等于测量出来的裂纹扩展长度加上预制缺口的曲率半径0.05mm;W为试验件的宽度;f(a/W)是形状修正因子,其表达式为:
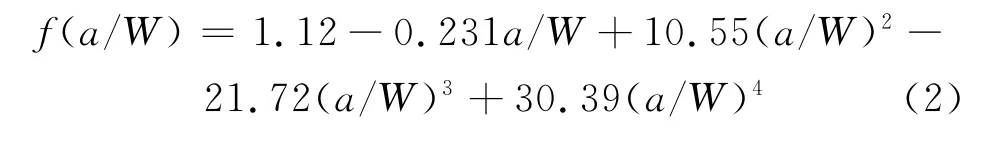
图2所示即为不同预腐蚀损伤试件得到的裂纹扩展速率随应力强度因子的变化曲线,从图中可以明显看出,在相同应力强度因子情况下,腐蚀损伤严重的试验件的裂纹扩展速率确实会高于腐蚀较轻的试验件,说明预腐蚀损伤确实对裂纹扩展影响比较强烈;预腐蚀试件的裂纹扩展的分散性很强,并且可以在很低的应力强度因子条件下扩展。这说明基于线弹性力学(LEFM)模型,利用应力强度因子(SIF)作为描述这种腐蚀疲劳裂纹,尤其是短裂纹存在很大的局限性,需要根据短裂纹不同于长裂纹的特点进行修正。
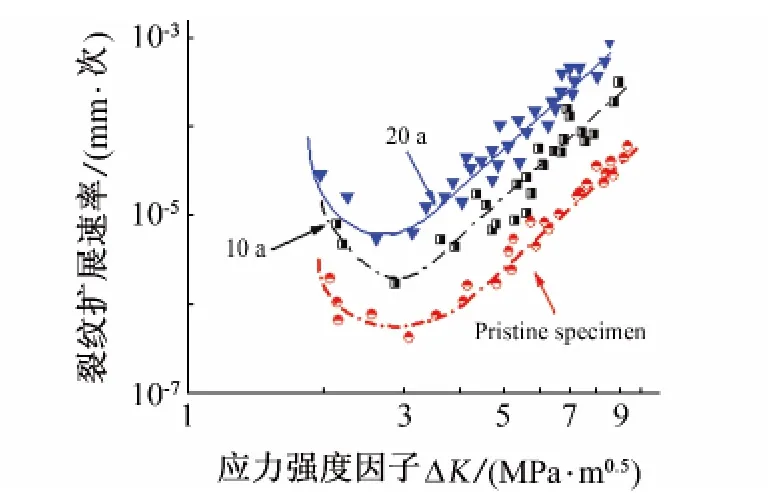
图2 裂纹扩展速率随应力强度因子ΔK的关系Fig.2 Crack growth rates againstΔK
2.2 预腐蚀疲劳裂纹扩展模型的建立
线弹性模型指出疲劳裂纹扩展可以用如式(3)所示的关系进行表征:
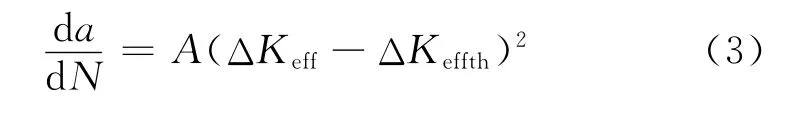
式中:A是与材料以及环境相关的常数,ΔKeff是有效应力强度因子范围,如下式所示:
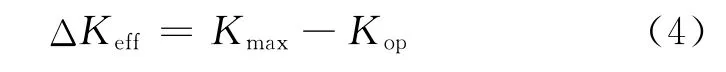
式中:Kmax是疲劳应力循环中的最大应力强度因子,Kop是裂纹面张开瞬间对应的应力强度因子。ΔKeffth是疲劳裂纹扩展门槛值。在双对数坐标系下,式(3)所代表的是一条斜率为2的直线,这与图2不符,这说明用式(3)描述进门槛值的疲劳裂纹扩展行为存在局限性。
这是因为短裂纹存在与长裂纹行为特征有差别。由于应力集中,裂纹尖端不可避免会有一个区域范围内的应力值超过材料的屈服强度而产生塑性变形。对于长裂纹,该塑性区的范围与裂纹的长度之比很小可以忽略不计,因此线弹性理论适用,而短裂纹尖端的弹塑性区相对其本身长度不可忽略,短裂纹在塑性区域扩展呈现弹塑性行为特征。(2)裂尖应力强度因子低于长裂纹所对应的扩展门槛值ΔKeffth,短裂纹仍然可以扩展,如图2所示。(3)疲劳短裂纹扩展存在很强的闭合效应,对于裂尖前方的驱动力(即应力强度因子)有影响。以上三方面是将线弹性理论应用于短裂纹时所必须进行的修正。针对裂纹尖端的弹塑性,Irwin提出了可以将裂纹长度进行修正,计入该塑性区的影响,如下式所示:

式中:σmax是最大应力,σr为屈服强度,amodified为修正后的裂纹长度,Lplastic为裂纹前方塑性区的尺寸,其表达式为:

该塑性区没有考虑腐蚀损伤对塑性区的影响,但是由于预腐蚀铝合金表面的腐蚀坑同样会引起应力集中,从而对弹塑性区域尺寸产生变化。考虑利用文献[3]中使用的参数孔蚀率α作为描述腐蚀损伤的程度,定义腐蚀影响系数D(α),对裂尖弹塑性区尺寸进行修正,即:
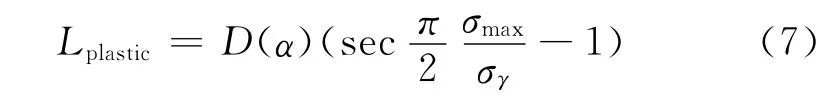
显然当α→0⇒D(α)→1,α→1⇒D(α)→某一上界,且合理假设D(α)具有如下的形式:
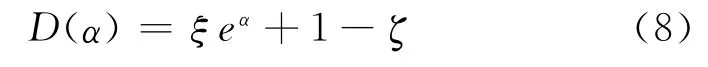
式中:0<ζ<1为待定常数。
短裂纹的尺度已经与铝合金晶粒尺寸接近,会受到材料缺陷的影响,从而对其应力强度因子产生影响,因此需要对材料的微缺陷影响进行修正。A.J.McEvily建议应力强度因子的计算公式可以表达为:
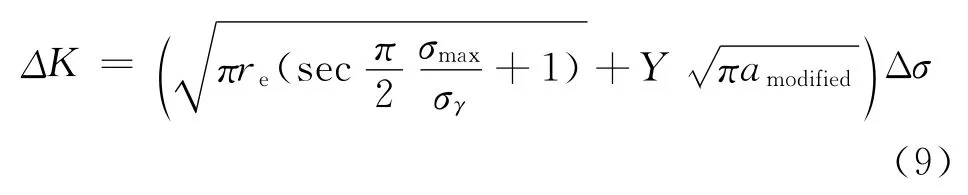
式中:Y为形状修正因子,re为材料内部隐性缺陷的尺寸。对于完好试件,re为恒定值,但是对于预腐蚀试验件,该值会受到腐蚀的影响而有所变化。式(9)中项就代表材料缺陷对扩展驱动力的贡献。对于长裂纹,该项可以忽略不计,式(9)退化为长裂纹的应力强度因子表达式。
裂纹尖端前部的闭合效应在短裂纹阶段影响尤其显著,所引起的新形成裂纹在原有裂纹尖端塑性区闭合效应按照文献[12]提供的方式用式(10)进行修正:
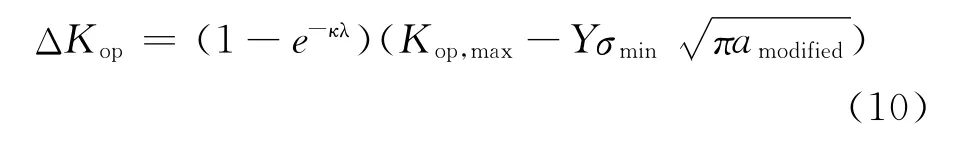
式中:κ是材料常数,σmin是疲劳应力循环中的最小应力值,λ是新形成的裂纹长度,对于光滑试件,λ可以从试件表面测量得到;对于含缺口试件,可以从缺口根部测量得到,初始裂纹尺寸a0就是缺口的深度;Kop,max表征裂纹的张开程度。
将式(5)、(7)~(10)带入式(3),可得

式中:M为修正后的裂纹扩展驱动力,其表达式如下:
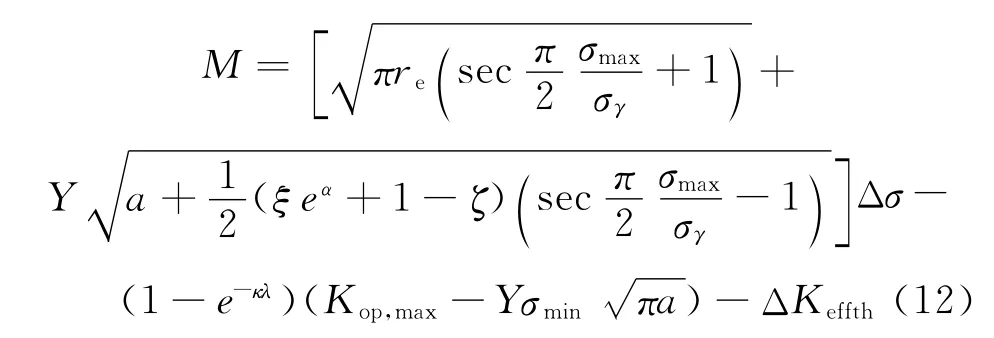
式中:re、α反应腐蚀的影响;Kop,max、ζ、κ为待定材料常数,为了简化模型,设这些参数与腐蚀无关;α、λ分别从预腐蚀试验和疲劳试验中测量计算得到;对于本工作所采用的试件,Y=0.73,已有的研究建议对于腐蚀铝合金的ΔKeffth非常低,因此这里对于含腐蚀损伤试验件,令ΔKeffth=0。
利用科士达拍摄的试件表面腐蚀形貌照片,借助于文献[3]提供的数字图像处理方法得到不同腐蚀年限的孔蚀率值,结果为α|10a=0.004 1,α|20a=0.025 2,a|0α=0。
利用图2中的裂纹扩展速率试验数据,基于式(11)的目标函数利用MATLAB软件编程建立非线性规划模型,优化得到各个参数如下所示:

利用式(11)得到的拟合结果与试验结果对比如图3和表1所示,可以看出拟合效果总体上较为满意。但是对于腐蚀损伤程度较重的20a试件试验结果线性度明显低于未腐蚀试验件的结构,说明该模型对于腐蚀的影响考虑还有待进一步改进。在修正的扩展模型中,不存在图2出现的裂纹扩展速率先降低后增高的趋势,而且能够将短裂纹阶段和长裂纹阶段的裂纹扩展速率用统一的模型进行描述。
3 结论
(1)在线弹性疲劳裂纹扩展模型的基础上考虑短裂纹以及腐蚀损伤的影响,修正了裂纹扩展驱动力的表达式,进而建立了弹塑性预腐蚀疲劳裂纹扩展速率的表征模型。
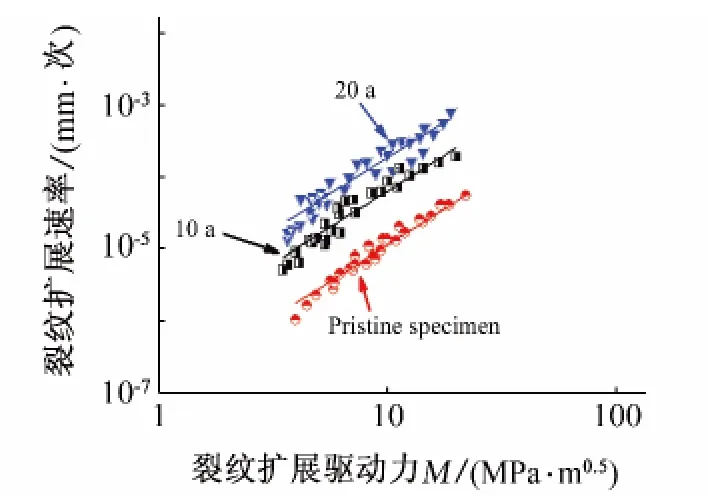
图3 裂纹扩展速率随裂纹扩展驱动力的关系Fig.3 Crack growth rate against M

表1 拟合结果分析Tab.1 Analysis of fitting results
(2)所建立的弹塑性预腐蚀疲劳裂纹扩展模型可以对于预腐蚀疲劳长裂纹和短裂纹的扩展速率进行统一化的描述,与线弹性裂纹扩展模型相比,其表征的范围大大扩展,而且预测效果良好。该模型可以为铝合金构件的寿命预测以及损伤容限评估提供更精确的理论参考。
[1]李旭东,刘治国,穆志韬.基于短裂纹的LD10CZ铝合金腐蚀预疲劳裂纹扩展[J].海军航空工程学院学报,2013(1):47-52.
[2]李旭东,王玉刚,苏维国.预腐蚀LY12CZ铝合金疲劳裂纹扩展行为研究[J].青岛科技大学学报:自然科学版,2013(2):182-187.
[3]李旭东.铝合金腐蚀环境下疲劳短裂纹演化规律的表征[D].北京:清华大学硕士学位论文,2011.
[4]LI X D,WANG X S,REN H H,et al.Effect of prior corrosion state on the fatigue small cracking behaviour of 6151-T6aluminum alloy[J].Corros Sci,2012,55(2):26-33.
[5]李旭东,刘治国,穆志韬.基于马尔可夫链模型的铝合金预腐蚀疲劳裂纹扩展表征[J].环境技术,2012(6):19-22.
[6]李旭东,穆志韬,孔光明,等.材料疲劳裂纹门槛值测定方法研究[J].装备环境工程,2014,11(1):82-85,92.
[7]李旭东,刘治国,穆志韬.基于神经网络的金属材料疲劳裂纹扩展规律的预测[J].新技术新工艺,2013(11):66-68.
[8]MCEVILY A J,ISHIHARA S.On the dependence of the rate of fatigue crack growth on the(2a)parameter[J].International Journal of Fatigue,2001(23):115-120.
[9]WARD-CLOSE C M,BLOM A F,RITCHIE R O.Mechanisms associated with transient fatigue crack growth under variable-amplitude loading:an experimental and numerical study[J].Engineering Fracture Mechanics,1989,32(5):613-651.
[10]李旭东,刘治国,穆志韬.基于飞行载荷的LC9铝合金腐蚀疲劳裂纹扩展[J].腐蚀与防护,2013,34(11):985-988.
[11]KIKUKAWA M,JONA M,TANAKA K,et al.Measurement of fatigue crack propagation and crack closure at low stress intensity level by unloading elastic compliance method[J].Journal of the Society of Materials Science,1976,25(6):899-903.
[12]MINAKAWA K,NAKAMURA H,MCEVILY A J.Prediction of the behaviour of small fatigue cracks[J].Scripta Metall,1984,18(3):1371-1375.
