缔合勒让德函数的解析表达式研究

张捍卫 李明艳 雷伟伟

1 河南理工大学测绘学院，焦作市世纪大道2001号，454003

勒让德方程在物理和工程中具有广泛应用。Boyd［1］给出切比雪夫多项式、勒让德多项式和雅可比多项式之间的理论关系，Parodi［2］利用勒让德函数的级数展开式系数来模拟签名特征，Morais［3］构建了一个适用于长椭球形状的完备正交函数系，Yalcnbas［4］在近似求解第二类线性Fredholm 积分方程时引入勒让德多项式，Liu［5］利用勒让德多项式生成的正交小波基进行偏微分方程的数值求解，Vladimir［6］也研究了勒让德多项式和其他正交函数系之间的理论关系。在国内，张传定［7］利用球面上的正交函数系研究了物理大地测量中的一阶、二阶梯度边值问题，张玉灵［8］根据勒让德函数的递推公式和基本性质推导了不同阶次勒让德函数的加权正交性，吴星［9］介绍了勒让德函数的多种递推计算方法，王建强［10］指出跨阶次递推法是计算超高阶次勒让德函数的较优方法，刘缵武［11］提出一个修正的勒让德函数递推算法，黄国蓝［12］利用理论计算和数值方法对勒让德多项式进行分析，区家明［13］利用勒让德多项式建立小尺度地磁场模型。但是，到目前为止，还没有一个适用于任意阶次的勒让德函数解析表达式。本文把任意阶次的勒让德函数表示为三角函数的倍角形式，不但方便勒让德函数对角度求导数和积分，以研究其加权正交性，而且可以简化其应用。

1 勒让德函数的定义与其级数展开式

1.1 勒让德函数的定义

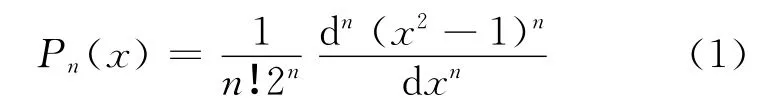
勒让德函数的定义是［14］：式中，n称为阶，且n∈N，N 是自然数集合。缔合勒让德函数的定义是：

式中，m称为次（级），m∈N，且m≤n。显然，当m＝0时，

式中，x是属于区间［－1，1］的实数。

1.2 勒让德函数的级数展开式

由于

式中，k∈N，！表示阶乘。当l≥n时，xl对x的n阶导数是：

式中，l∈N。利用式（4）和式（5），可把式（1）写为：

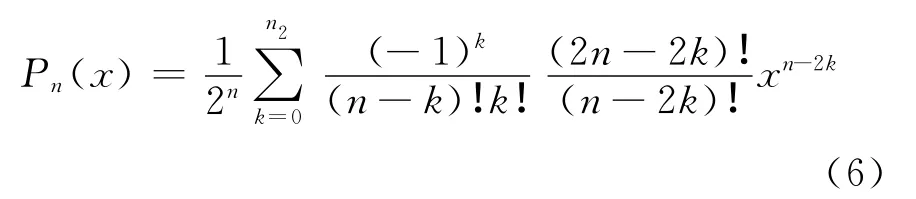
式中，n2＝intn／［ ］2 ，以保证n－2k≥0。

把式（6）代入式（2），并考虑到式（5），则式（2）可写为：

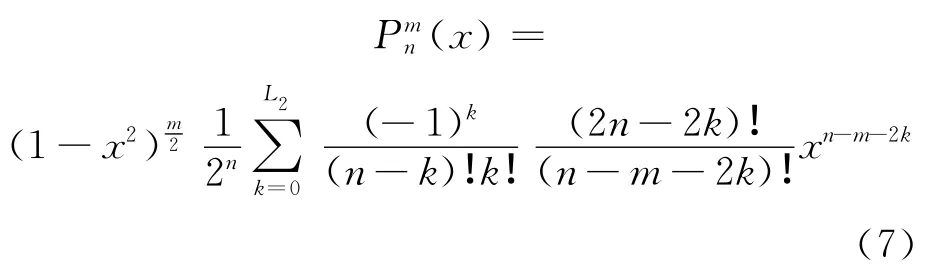
2 勒让德函数的三角函数形式

2.1 以三角函数幂次形式表示的缔合勒让德函数

假设x＝cosθ，θ∈［0，π］，则式（7）写为：

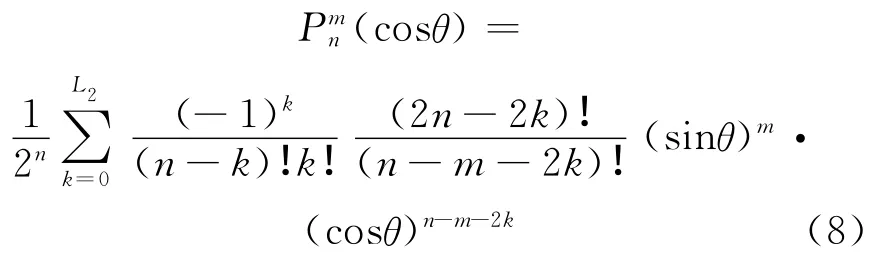
同样，sinθ和cosθ的幂次必须大于等于0。

2.2 以三角函数倍角形式表示的勒让德函数

勒让德函数的生成函数是：

式中，w为复数变量，且其模数。如果令x＝cosθ，则式（9）等号右边可写为：

式中，i2＝－1。因为

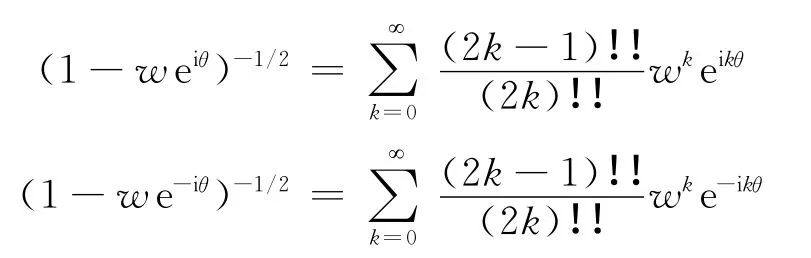
利用无穷级数的柯西法则：

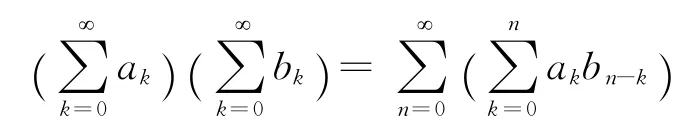
有：

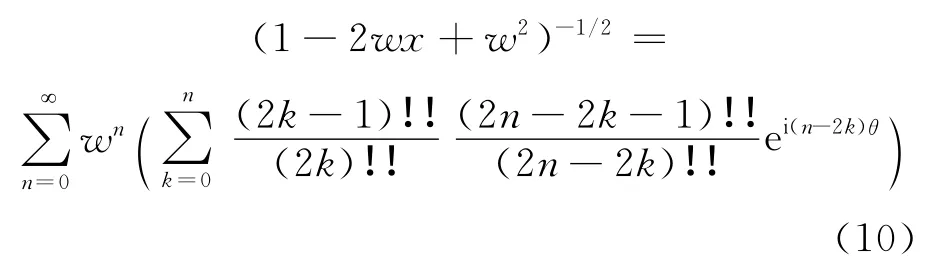
比较式（9）和式（10）可得：

当上式的k代换为（n－k）时，求和号内系数相等，只是ei（n－2k）θ变为e－i（n－2k）θ，因此有：

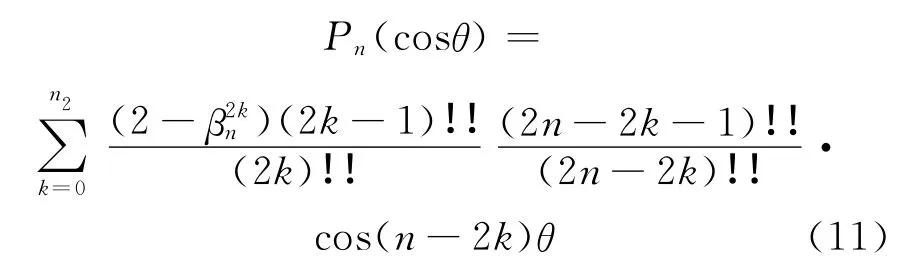
此时约定：

式（11）就是以三角函数倍角形式表示的勒让德函数。

3 勒让德函数的递推公式

勒让德函数的递推公式［14］为：

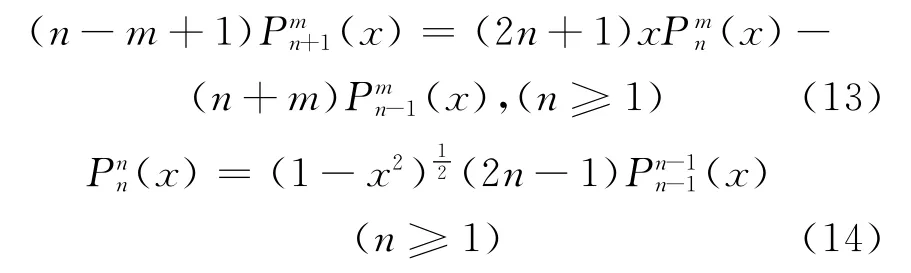
如果在式（13）中出现n－1＜m的情况，则设置为零。如果已知低阶次的勒让德函数的数值，原则上可利用式（13）和式（14）求得任意阶次勒让德函数的数值，但不能求得其解析表达式。如果能把也表示为式（11）的形式，则对于理论研究和实际应用来说将很有意义。另外，还有两个常用的递推公式［14］：

当式（8）代入式（16），又变为原来的式（8）。根据式（16），可得：

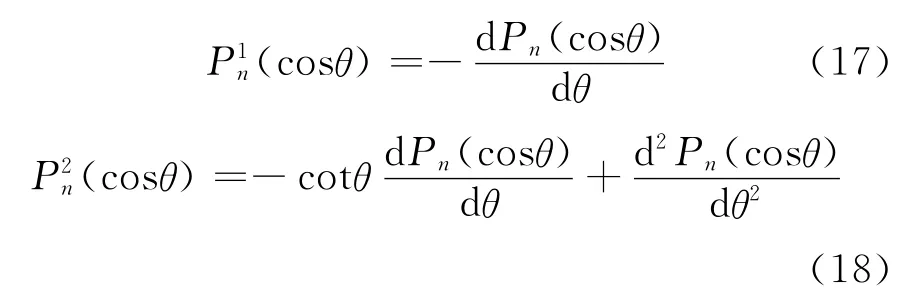
设式（11）求和号内的系数是ak，则式（17）可表示为：

利用勒让德微分方程：

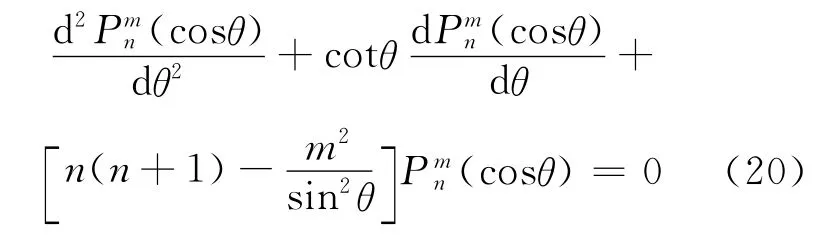
可把式（18）表示为：

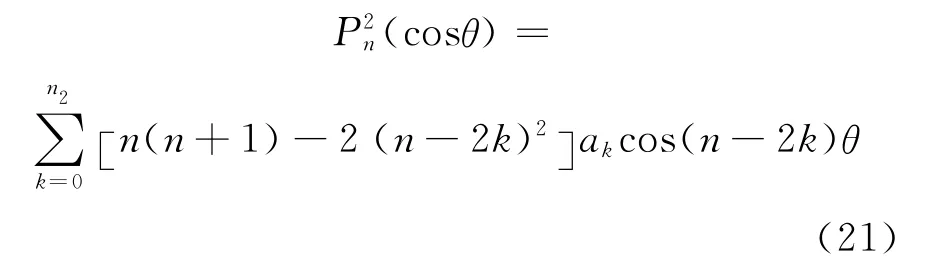
但不能推求m≥3情况下Pmn（cosθ）的解析表达式。

4 以三角函数倍角形式表示的缔合勒让德函数

4.1 整体代入法

因为

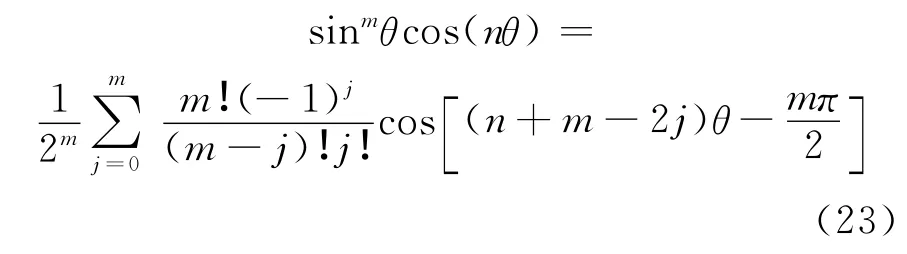
把以上两式代入式（8），可得：

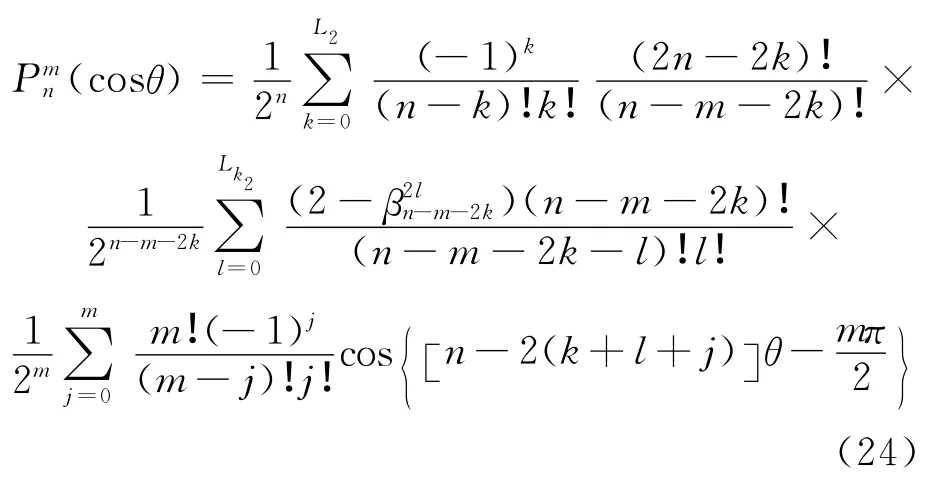
式中，Lk2＝int（L2－k）。3个求和号相乘有［1＋2（m＋1）个组合，且（k＋l）的最大值是L2。故有：

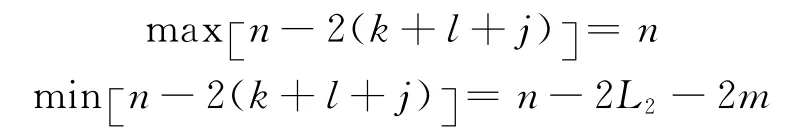
这样，在式（24）中，就有（L2＋m＋1）个倍角出现。但是，这些倍角中可能出现正负反对称情况，需根据m进行合并。最后，式（24）可化为：

4.2 逐步代入法

在n和m已知的情况下，定义2个数组：

把式（22）代入式（8），则有：

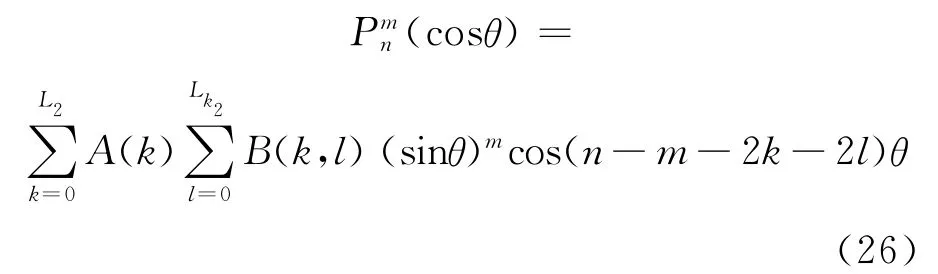
根据两个求和号结构，可把上式写为：

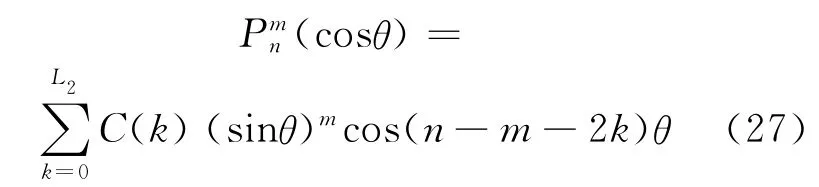
其中，

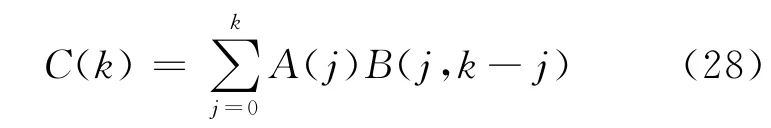
再把式（23）代入式（27），可得：

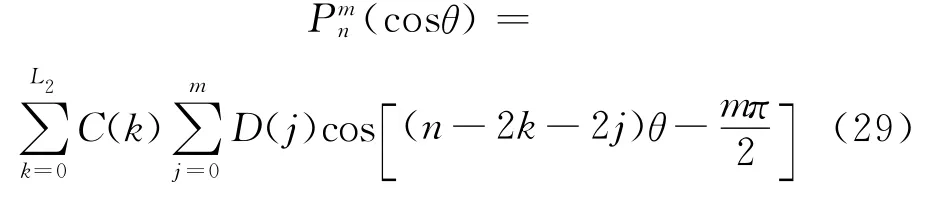
其中数组D（j）的定义是：

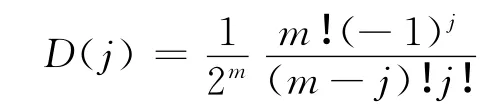
式（29）中，求和号相乘共有（L2＋1）（m＋1）个组合，这些组合中倍角的最大值和最小值分别是：

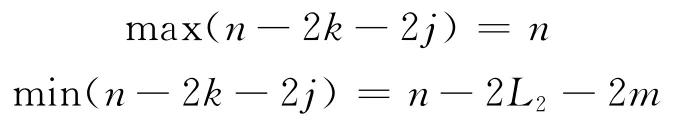
因此，式（29）可化为：

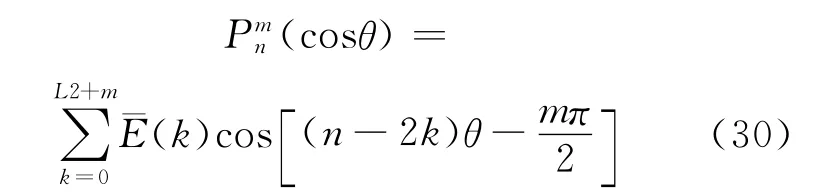
其中，当k≤L2且j≤m时，有：

当L2＋1≤k≤L2＋m且m≥1时，有：

式中，L3＝min（L2，L2＋m－k）。可见，如果采用逐步代入法，可得的具体解析表达式。在式（30）中，也有（L2＋m＋1）个倍角出现，但这些倍角中也可能出现正负反对称情况，此时需根据m数值进行合并，最后改化为式（25）的形式。

5 实际计算

在n和m确定的情况下，计算数组A（k）、B（k，l）和D（j），其中数组下标的取值范围分别是：

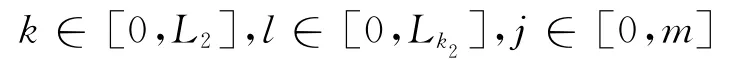
利用式（28）计算数组C（k），此时k取值范围同上。利用式（31）和式（32）计算数组，此时k的取值范围则是k∈［0，L2＋m］。

以式（25）为标准，表1 给出0～5 阶勒让德函数展开式，与有关文献完全一致，表明本文公式正确。

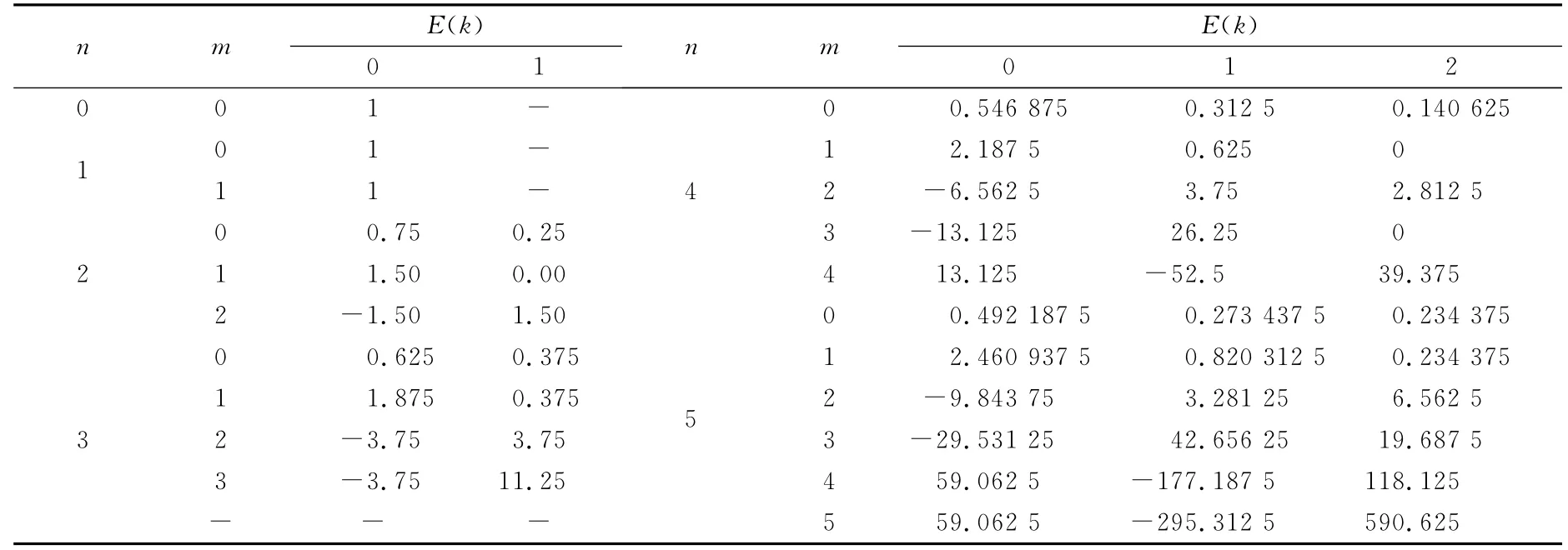
表1 0～5阶的勒让德函数的系数Tab.1 The coefficient of Legendre function until order 5

［1］Boyd J P，Petschek R.The Relationships between Chebyshev，Legendre and Jacobi Polynomials：The Generic Superiority of Chebyshev Polynomials and Three Important Exceptions［J］.Journal of Scientific Computing，2014，59（1）：1－27

［2］Parodi M，Gómez J C.Legendre Polynomials Based Feature Extraction for Online Signature Verification，Consistency Analysis of Feature Combinations［J］.Pattern Recognition，2014，47（1）：128－140

［3］Morais J.An Orthogonal System of Monogenic Polynomials over Prolate Spheroids in R3［J］.Mathematical and Computer Modelling，2013，57（3）：425－434

［5］Liu N，Lin E.Legendre Wavelet Method for Numerical Solutions of Partial Differential Equations［J］.Numerical Methods for Partial Differential Equations，2010，26（1）：81－94

［6］Vladimir G，Mariana M.Orthogonal Polynomials and Related Special Functions Applied in Geosciences and Engineering Computations［J］.Komunikacie，2010，12（1）：12－15

［7］张传定，陆仲连.广义球谐函数及其在梯度边值问题的应用［J］.测绘学报，1998，27（3）：252－258（Zhang Chuanding，Lu Zhonglian.General Spherical Harmonics and Its Application［J］.Acta Geodaetica et Cartographica Sinica，1998，27（3）：252－258）

［8］张玉灵，刘缵武.不同阶次连带勒让德函数的正交性［J］.大学数学，2006，22（2）：108－111（Zhang Yuling，Liu Zanwu.Orthogonal Property of Different Levels and Orders of Associated Legendre Functions［J］.College Mathematics，2006，22（2）：108－111）

［9］吴星，刘雁雨.多种超高阶次缔合勒让德函数计算方法的比较［J］.测绘科学技术学 报，2006，23（3）：188－191（Wu Xing，Liu Yanyu.Comparison of Computing Methods of the Ultra－High Degree and Order［J］.Journal of Zhengzhou Institute of Surveying and Mapping，2006，23（3）：188－191）

［10］王建强，赵国强，朱广彬.常用超高阶次缔合勒让德函数计算方法对比分析［J］.大地测量与地球动力学，2009，29（2）：126－130（Wang Jianqiang，Zhao Guoqiang，Zhu Guangbin.Contrastive Analysis of Common Computing Methods of Ultra－Hing Degree and Order Fully Normalized Associated Legendre Function［J］.Journal of Geodesy and Geodynamics，2009，29（2）：126－130）

［11］刘缵武，刘世晗，黄欧.超高阶次勒让德函数递推计算中的压缩因子和Horner求和技术［J］.测绘学报，2011，40（4）：454－458（Liu Zanwu，Liu Shihan，Huang Ou.Scale Factors in Recursion of Ultra－High Degree and Order Legendre Functions and Horner’s Scheme of Summation［J］.Acta Geodaetica et Cartographica Sinica，2011，40（4）：454－458）

［12］黄国蓝，樊江红，卢方武.勒让德多项式的数值分析及应用研究［J］.高师理科学刊，2012，32（6）：7－10（Huang Guolan，Fan Jianghong，Lu Fangwu.The Numerical Analysis and Applied Research of Legendre Polynomial［J］.Journal of Science of Teachers’College and University，2012，32（6）：7－10）

［13］区家明，杜爱民，徐文耀，等.小尺度地磁场勒让德多项式建模方法［J］.地球物理学报，2012，55（8）：2 669－2 675（Ou Jiaming，Du Aimin，Xu Wenyao，et al.The Legendre Polynomials Modeling Method of Small－Scale Geomagnetic Fields［J］.Chinese Journal of Geophysics，2012，55（8）：2 669－2 675）

［14］方俊.重力测量与地球形状学［M］.北京：科学出版社，1975（Fang Jun.Gravity Measurement and Shape of the Earth［M］.Beijing：Science Press，1975）