联合反演模型中相对权比的约束反演
2015-02-15独知行张显云
张 俊 独知行 杜 宁 张显云
1 山东科技大学测绘科学与工程学院,青岛市经济技术开发区前湾港路579号,266590
2 贵州大学矿业学院,贵阳市吉林新村,550025
目前,约束反演和联合反演是地球物理和大地测量反演研究的热点[1-6]。由于反演分析方法本质上是由“现象”推求“原因”,其推求“原因”的能力取决于所建立的模型能多大程度上反映二者之间的真实联系,因此,解的不适定性即成为反演分析方法的固有特性[7-8]。目前,解决不适定问题的主要手段是建立多种数据的联合反演模型[1-12],并利用模型参数的某些先验信息对参数可能的数值区间予以限制来实现的[1-2]。在这一过程中,由于对模型参数进行了一定的约束,从而使反演搜索区间大大缩小,在提高解算效率的同时,也改善了模型参数解的不适定问题。在模型具体解算时,不同数据对问题分析的贡献是由各类数据在目标函数中的相对权比来决定的。文献[1]指出,相对权比通过影响模型空间交集的大小,从而影响联合反演模型空间的大小。相对权比最初基本上采用观测值初始方差或简单的试错法确定,具有一定的主观性[11-12]。文献[13]提出将相对权比与模型参数一同作为待反演参数参与联合反演模型函数极小化求解过程,从而避免主观性;许才军等[14-16]讨论了联合反演中各类观测值相对权比的几种确定方法,认为赫尔默特方差分量估计是最优方法。以上方法可归纳为4种:第一种,根据数据种类数的简单平均分配;第二种,相对权比与模型参数一同反演;第三种,利用赫尔默特方差分量估计法原理,对不同数据的先验精度进行调整,然后依据调整后的精度确定相对权比;第四种,根据先验信息,基于某些经验直接给出相对权比值。本文借鉴第二和第四种方法的思想,即采取相对权比与模型参数一起参与模型全局极小化反演过程来确定相对权比,但必须根据数据先验信息,事先对相对权比给予一定约束,从而得到较为合理的反演分析结果。
1 联合反演模型的目标函数
大地测量联合反演是指利用包括大地测量数据在内的两种或两种以上的观测量(如测点位移和主应力资料等)求解未知参数的反演方法[1,6]。为正确反映不同观测量对模型参数求解的贡献度,在构造模型时,需要对各类数据赋予一定的权比,恰当的相对权比可使反演结果更合理、更真实。相对权比的数值大小反映了模型对不同观测量的拟合程度。设有模型:

式中,假定有n类观测数据,则有λ1+λ2+…+λn=1,且0≤λi≤1,其中λi为第i类观测数据的相对权比值。m为参数空间,φi(m)为联合反演模型中第i类目标的子函数,一般取φi(m)=(fi(m)-di)2,其中fi(m)为第i类数据与反演参数之间的正演函数,di为第i类观测数据。当有可靠精度信息时,φi(m)可取加权形式,即取φi(m)=Pi(fi(m)-di)2。
假定各类数据已经过归一化等数据预处理,从而建立模型(1),则根据多种数据进行联合反演的问题,可归结为求能使模型(1)的目标函数取得极小值的参数m的最优化问题。
2 联合反演模型相对权比的约束反演
建立模型(1)后,大地测量联合各类数据(如地质、地震、地球物理数据)进行反演分析时,其任务即为选择、利用某种全局最优化方法,来固定模型(1)的参数空间,并进行相关评价和解释。本文仅通过数值实验讨论模型参数的获取问题。后续评价与解释一般需要结合具体实际才能进行,因此不作深入讨论。
模型(1)中目标函数极小值的取得,明显受相对权比值λ的影响。只有合理地确定各类数据的相对权比关系,才能获得合理的参数反演解。文献[13]提出,将模型(1)中的相对权比作为未知参数,与其他模型参数一同参与反演,取得了较好的应用效果。这种方法的优势在于可避免人为确定相对权比的主观性,但是,却忽略了反演的本质是一种纯粹的数学方法,有时得不到切合实际的反演结果。如果能够根据数据本身的某些先验信息,对相对权比值上下界附加某种约束,既可避免人为选择的主观性,又顾及了数据的原本特质。若对参数也有一定的了解,则对参数也附加一定的约束,可望得到较好的反演结果。为此,可在模型(1)的基础上,对参数和相对权比都施加一定的约束,则整个反演模型即为模型(1)与如下约束模型的复合模型:
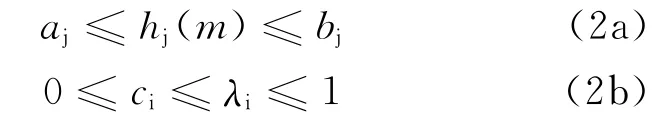
式(2a)中,hj(m)表达了对参数的某种约束。h(m)可以是线性也可以是非线性的,当有多个约束时,hj(m)中下标j表达了对参数的多种约束。式(2b)是对相对权比的约束,ci表示第i类数据与模型参数一起作为待反演参数时的下界值。
联合反演模型相对权比的约束反演值就是在同时满足模型(1)和模型(2)的条件下所得到的相对权比的反演值,而最终联合反演模型参数m值就是在相应的相对权比值下的反演值。具体实施过程如下。
第一步,建立模型(1)。模型(1)的建立,关键在于能否正确建立各类数据与待反演参数的数学物理描述。一般来讲,可直接利用现有的大地测量、地质、地球物理中已建立的成熟模型,如利用基于力学模式的弹性力学模型,附加一定边值条件,结合有限元方法,来反演物质弹性模量、泊松比、边界力等。
第二步,对原始数据进行分析,获取数据和待反演参数的先验信息。如针对观测数据,可考虑从数据内外符合精度、是否包含系统误差等数据质量信息着手,分析数据相对质量好坏,从而为第三步确定相对权比约束提供依据;针对模型参数,可根据已有实验值或经验,确定模型(2)中参数或参数函数的约束端点值a、b,如地壳弹性模量或密度等数值一般都有相对可靠的范围,利用这些信息很容易建立约束模型(式(2a))。
第三步,根据第二步分析结果或已有经验,对相对权比附加适当约束,即确定模型(2b)中的c值以建立模型(2b),从而对相对权比进行有效的下界约束。
第四步,利用某种全局最优化方法,如模拟退火或改进的模拟退火法、遗传算法和区间算法等作为反演分析的数学方法,确定模型参数初始值X(0),并设定解的搜索方式,在模型(2)的约束下更新模型参数X(0)和相对权比值λ0,得到相对权比和参数更新值λ(k)和X(k)。
第五步,比较第四步中X(k)与X(0)作用于模型(1)的目标函数值Φ(λ,X),当相邻两次目标函数值差值的范数小于事先设定的阈值ε时,停止迭代过程;否则,重复第四、五步,不断更新X(0)和λ0并得到更新值X(k)和λ(k),直到满足|Φ(λ(k),X(k))-Φ(λ(0),X(0))|≤ε时为止。迭代终止后,取Xk作为最终反演模型参数解,λ(k)为对应最终相对权比的反演值。
3 算例及分析
本文算例源于文献[1]。设某一大地测量反演问题建立的线性反演模型为V=Bx-l,在该模型中,x为待反演的模型参数(某滑坡的几何变化信息),包括4个分量:x1(长度)、x2(宽度)、x3(深度)和x4(倾斜)。所附加的线性不等式约束为Gx≤W。同时,由监测得到的参数变化范围是-0.2≤xi≤2(i=1,2,3,4),反演参数的真值为=[-0.07-0.2 0.20 0.37]T,具体参见文献[1]。这里对原算例进行如下改化:令T=,并将L分为3组,即令L,相应地T=[BTGT],则原问题可简单地看作由3类数据建立的不同线性反演模型构成的联合反演问题。鉴于实际中模型和观测数据都不可避免地含有误差,因此在3组观测数据及相应系数矩阵中分别模拟了大小不同的正态随机误差(表1)。

表1 分组后的原始数据及模拟误差Tab.1 Grouped original data and simulation error
考虑到参数满足约束条件-0.2≤xi≤2(i=1,2,3,4)(相当于模型(2a)中,h(x)=x,a=-0.2,b=2.0情形),采用下列方案进行反演计算,各方案反演结果列于表2(其中为参数反演值,‖Δx‖ =‖x-‖ 为参数反演值与真值之差的范数)。
方案1 3类数据按各自模拟方差定权,相对权比均取为1/3进行联合反演;
方案2 3 类数据按各自模拟方差定权,式(2)中相对权比下界约束值分别取c1=0.1,c2=1/3,c3=0.1,将相对权比与模型参数一并进行联合反演;
方案3 3类数据按各自模拟方差定权,式(2)中相对权比下界值分别取c1=0.1,c2=1/3,c3=0.2,将相对权比与模型参数一并进行联合反演;
方案4 3类数据按各自模拟方差定权,式(2)中相对权比下界值分别取c1=0.2,c2=1/3,c3=0.1,将相对权比与模型参数一并进行联合反演;
方案5 3类数据按各自模拟方差定权,相对权比与模型参数一并进行联合反演,但不对相对权比作任何约束,即式(2)中相对权比下界值分别取c1=c2=c3=0。
对表2各方案反演结果进行对比可以看出,根据模拟误差精度对相对权比进行不同约束反演,得到不同的反演结果。在对相对权比进行约束时,考虑到第二组数据模拟精度最高、第三组次之、第一组最差,在3类数据联合反演时,充分利用先验精度信息,考虑3组数据的贡献度。比如对于第二组数据,由于其精度最高,可考虑使其相对权比具有不小于1/3的贡献度,而对其余两组数据进行不同下界阈值的约束实验。结果显示,当对相对权比按精度进行符合实际的约束反演时,反演结果有显著改善(方案3),这是因为方案3对相对权比约束的下界值很好地顾及了3组数据的精度情况,正确反映了各类数据在联合反演中应有的贡献度。当相对权比约束不符合实际时,反演结果反而不及将相对权比简单平均分配的反演结果好。如方案2认为第一组数据和第三组数据至少应该有相同的贡献,而方案4认为第一组数据应有高于第三组数据的贡献。显然,根据模拟误差先验信息,这两种约束都不合理。当对相对权比不作任何约束并将相对权比与待反演参数一起反演时,结果最差(方案5)。并且从结果看,几乎完全拟合了第一组数据,而第一组数据恰恰是精度最差的。这说明,仅将相对权比简单地与其他参数一起作为反演参数参与反演计算是一种纯粹的数学方法,没有顾及数据本身的实际情况。

表2 各方案的反演结果Tab.2 The inversion results of each scheme
4 结 语
实验表明,将相对权比与待反演参数一起作为未知参数参与反演的方法是可行的,但必须根据数据质量情况或地球物理的某些先验信息,对相对权比进行适当的约束。考虑到通常事先难以对各类数据有精确的了解,这种约束一般也不宜太强。如针对第二组数据,因其精度最高,仅根据模拟误差精度情况对其相对权比下限进行不低于平均贡献度的约束,而并未对其上限作进一步约束。事实上,当对数据缺乏足够了解时,不适当的约束反而会导致结果扭曲。因此,当缺乏数据先验信息时,联合反演分析中相对权比如何确定仍然是值得进一步研究的问题。
[1]王乐洋,许才军.等式约束反演与联合反演的对比研究[J].大地测量与地球动力学,2009,29(1):74-78(Wang Leyang,Xu Caijun.Comparative Research on Equality Constraint Inversion and Joint Inversion[J].Journal of Geodesy and Geodynmics,2009,29(1):74-78)
[2]王乐洋,朱建军.附不等式约束的大地测量反演[J].大地测量与地球动力学,2008,28(1):109-114(Wang Leyang,Zhu Jianjun.Geodetic Inversion Theory Constrained with Inequalty[J].Journal of Geodesy and Geodynmics,2008,28(1):109-114)
[3]Zeng Y H,Chen C H.Fault Rupture Process of the 20 September 1999Chi-Chi,Taiwan Earthquake[J].Bulletin of the Seismological Society of America,2009,99(5):1 088-1 098
[4]Ma K,Mori J,Jong L S,et al.Spatial and Temporal Distribution of Slip for the 1999 Chi-Chi,Taiwan Earthquake[J].Bulletin of the Seismological Society of America,2001,91(5):1 069-1 087
[5]Wald D J,Heaton T H.Spatial and Temporal Distribution of Slip for the 1992Landers,California Earthquake[J].Bulletin of the Seismological Society of America,1994,84(3):668-691
[6]Wright T J,Parsons B E,Jackson J A,et al.Source Parameters of the 1 October 1995 Dinar(Turkey)Earthquake from SAR Interferometer and Seismic Body Wave Modeling[J].Earth and Planetary Science Letters,1999,172:23-37
[7]赵少荣,於宗俦,陶本藻,等.动态大地测量反演理论及其若干应用[J].测绘学报,1993,22(4):241-248(Zhao Shaorong,Yu Zongchou,Tao Benzao,et al.Theory of Dynamic Geodetic Inversion and Its Applications[J].Acta Geodaetic et Cartographica Sinica,1993,22(4):241-248)
[8]独知行,卢秀山.基于力学模式的大地测量反演理论及应用[M].北京:地震出版社,2003(Du Zhixing,Lu Xiushan.Theory and Application of Geodesy Inversion Based on Mechanical Models[M].Beijing:Earthquake Press,2003)
[9]独知行,卢秀山,温兴水,等.中国大陆主要块体现今运动状态联合反演研究[J].山东科技大学学报:自然科学版,2006,25(1):17-20(Du Zhixing,Lu Xiushan,Wen Xingshui,et al.Joint Inversion on Present Motion State of the Main-Plates in Chinese Continent[J].Journal of Shandong University of Science and Technology:Natural Science,2006,25(1):17-20)
[10]Hartzell S H,Heaton T H.Inversion of Strong Ground Motion and Teleseismic Waveform Data for the Fault Rupture History of the 1979Imperial Valley California,Earthquake[J].Bulletin of the Seismological Society of America,1983,73(6):1 553-1 583
[11]Yagi Y,Kikuchi M.Source Rupture Process of the Kocaeli,Turkey,Earthquake of August 17,1999,Obtained by Joint Inversion of Near-Field Data and Teleseismic Data[J].Geophys Res Lett,2000,27:1 969-1 972
[12]Delouis B,Giardini D,Lundgren P,et al.Joint Inversion of InSAR,GPS,Teleseismic,and Strong-Motion Data for the Spatial and Temporal Distribution of Earthquake Slip:Application to the 1999Izmit Mainshock[J].Bulletin of the Seismological Society of America,2002,92(1):278-299
[13]独知行,欧吉坤,靳奉祥,等.联合反演模型中相对权比的优化反演[J].测绘学报,2003,32(1):15-19(Du Zhixing,Ou Jikun,Jin Fengxiang,et al.Optimization Inversion of the Relative Weight Ratioλin the Joint Inversion Models[J].Acta Geodaetic et Cartographica Sinica,2003,32(1):15-19)
[14]段虎荣,张永志.断层滑动特征与多种反演数据的相对权比关系研究[J].大地测量与地球动力学,2009,29(6):18-21(Duan Hurong,Zhang Yongzhi.On Relative Weight Ratio Relation Between Characteristics of Fault Slip and Various Type of Inversion Data[J].Journal of Geodesy and Geodynamics,2009,29(6):18-21)
[15]王乐洋,许才军,张朝玉.一种确定联合反演中相对权比的两步法[J].测绘学报,2012,41(1):19-24(Wang Leyang,Xu Caijun,Zhang Chaoyu,et al.A Two-Step Method to Determine Relative Weight Ratio Factors in Joint Inversion[J].Acta Geodaetic et Cartographica Sinica,2012,41(1):19-24)
[16]Xu Caijun,Ding Kaihua,Cai Jianqing,et al.Methods of Determining Weight Scaling Factors for Geodetic-Geophysical Joint Inversion[J].Journal of Geodynamics,2009,47:39-46
