灌注桩套管高频振动贯入过程中挤土效应研究
2015-02-15肖勇杰陈福全林良庆
肖勇杰,陈福全,林良庆
(福州大学 土木工程学院,福建 福州 350116)
1 引 言
灌注桩可根据土层分布情况任意变化桩长,不受土层变化限制,不需要接桩和截桩,无振动、无挤土、噪声小、承载力高,适用于城市高层建筑、港口工程及桥梁工程的基础。随着全套管振动取土灌注桩施工工艺的发展,灌注桩在实际工程中得到越来越广泛的应用,如图1 所示。该工艺采用大激振力高频振动锤和与之配套的水润滑装置,使套管与土的相互摩阻力显著降低,克服了采用静压沉管和低频振动时难以避免的土塞问题;该工艺的套管沉拔和取土等工序只需要一套设备就可完成,比现有相似设备的工效高出2 倍以上[1]。然而,灌注桩套管高频振动贯入会产生明显的挤土效应,这种影响主要表现在:套管周围土体产生挤土位移,可能使邻近桩体上浮、桩位偏移甚至导致桩体断裂[2];套管贯入过程中套管周围土体应力状态发生改变,将产生很高的超孔隙水压力,过高的超孔隙水压力会妨碍套管贯入,甚至对邻近既有桩体和周围构筑物产生不良影响[3]。

图1 全套管振动取土灌注桩施工Fig.1 Construction of the cast-in-place piles with sleeves with vibratory hammers
国内外对套管或管桩静压贯入问题的研究开展较早,研究静压沉管机制以及沉管过程中挤土效应变化规律的方法也比较丰富多样[4-7]。与静压沉管方法相比,套管高频振动贯入过程是一个非常复杂的结构与土体相互作用的力学过程,不仅涉及到振动与挤压对周围土层的强烈扰动作用,还涉及到套管内外侧壁与土体间的反复剪切与滑移[8]。目前,关于灌注桩套管高频振动贯入机制和挤土效应研究还十分少见。国内一些学者通过现场试验方法,分析振动沉拔套管过程中土体位移、应力及孔隙水压力的变化情况[3,9]。虽然现场试验能直观反映实际情况,但取得数据有限,无法深入分析相应的作用性状与机制。
在Henke 等[10-11]提出的分析方法基础上,本文采用有限元与无限元耦合方法,研究灌注桩套管高频振动贯入全过程,揭示套管贯入过程中不同深度和位置处的挤土位移、超孔隙水压力随沉管过程的变化规律及挤土效应的影响范围。
2 问题的描述与分析方法
2.1 几何模型
采用Abaqus/Explicit 建立套管高频振动贯入黏土的有限元模型(见图2)。套管长L=20 m,外径D=1 m,壁厚为1.5 cm。有限元分析模型网格如图3 所示。近场域土体采用有限元模拟,有限元网格采用8 节点实体减缩积分单元C3D8R。为了消除振动波反射的影响,远场域土体采用无限元,无限元网格采用8 节点实体无限单元CIN3D8。灌注桩套管采用离散刚体单元R3D4,不考虑套管变形。
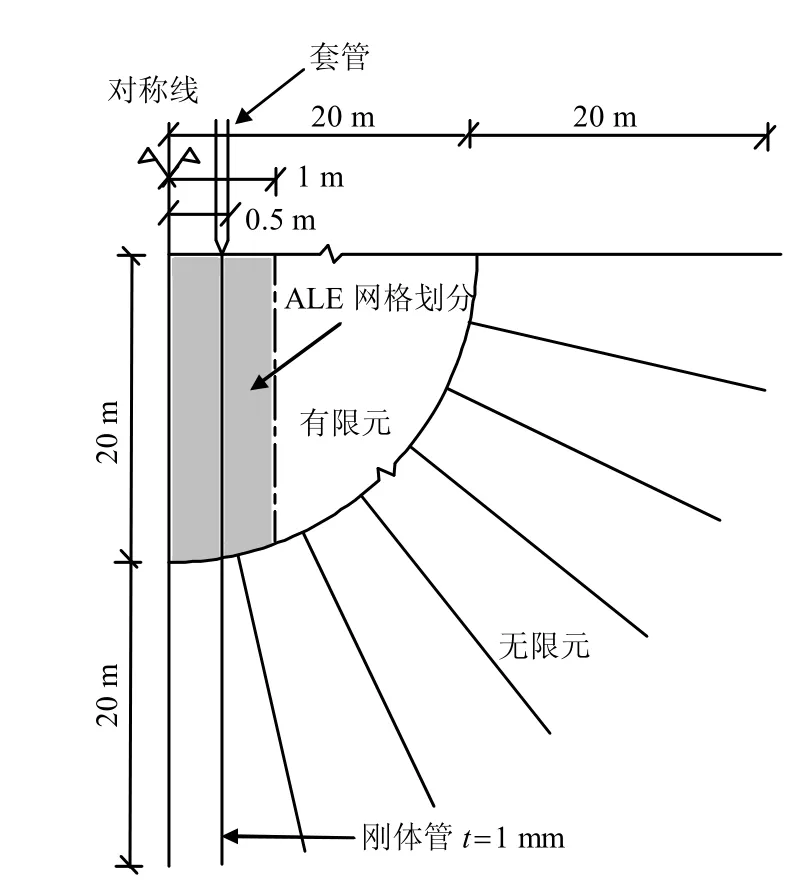
图2 有限元模型Fig.2 Finite element model
采用有限元模拟灌注桩套管高频振动贯入过程时,容易出现套管周围土体大变形、网格高度扭曲和边界条件改变明显等数值计算问题,导致计算结果不精确,甚至计算不收敛。为解决套管高频振动贯入过程中套管周围土体大变形和网格畸变等问题,套管附近1 m 范围内的土体单元采用任意拉格朗日-欧拉(ALE)自适应网格划分技术。
2.2 “拉链模型”有限元分析技术
Mabsout 等[12]最先应用有限元模拟桩的贯入过程。但在该模型中,桩预先贯入18 m,仅模拟剩下的锤击过程。随后,Mabsout 等[12]将一种称为“拉链模型”有限元分析技术应用于桩的贯入过程,在贯入轴向预留直径约为桩径1%的孔洞,预留孔洞在贯入过程中扩展,以便建立桩和土的接触。这种“拉链模型”分析技术也适用于套管高频振动贯入,即沿套管壁建一个壁厚t=1 mm 的刚体管,如图3 所示。套管贯入前,套管与周围土体设为无摩擦;套管贯入过程中,套管沿刚体管滑动,土与刚体管分开。采用这种方法,即可建立贯入套管与周围土体之间的接触。套管壁与土体的接触采用Coulomb 摩擦接触模型,刚体管和土设为光滑硬接触。
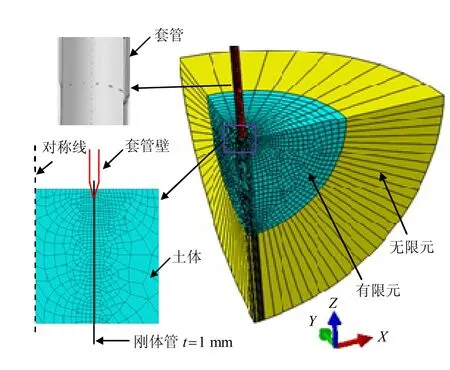
图3 有限元网格及“拉链模型”分析技术示意图Fig.3 Schematic of FEM meshes and zipper model analytical technique
2.3 孔压分析技术
由于Abaqus/Explicit 不提供孔压单元,只能进行总应力分析。假设套管贯入过程中黏土处于不排水状态,分别定义土体骨架有效应力-应变矩阵 D′和孔隙水应力-应变矩阵 Dw,总应力-应变矩阵 Dt为有效应力-应变矩阵D′与孔隙水应力-应变矩阵Dw之和,则不排水总应力-应变关系表达式为[6,13-15]
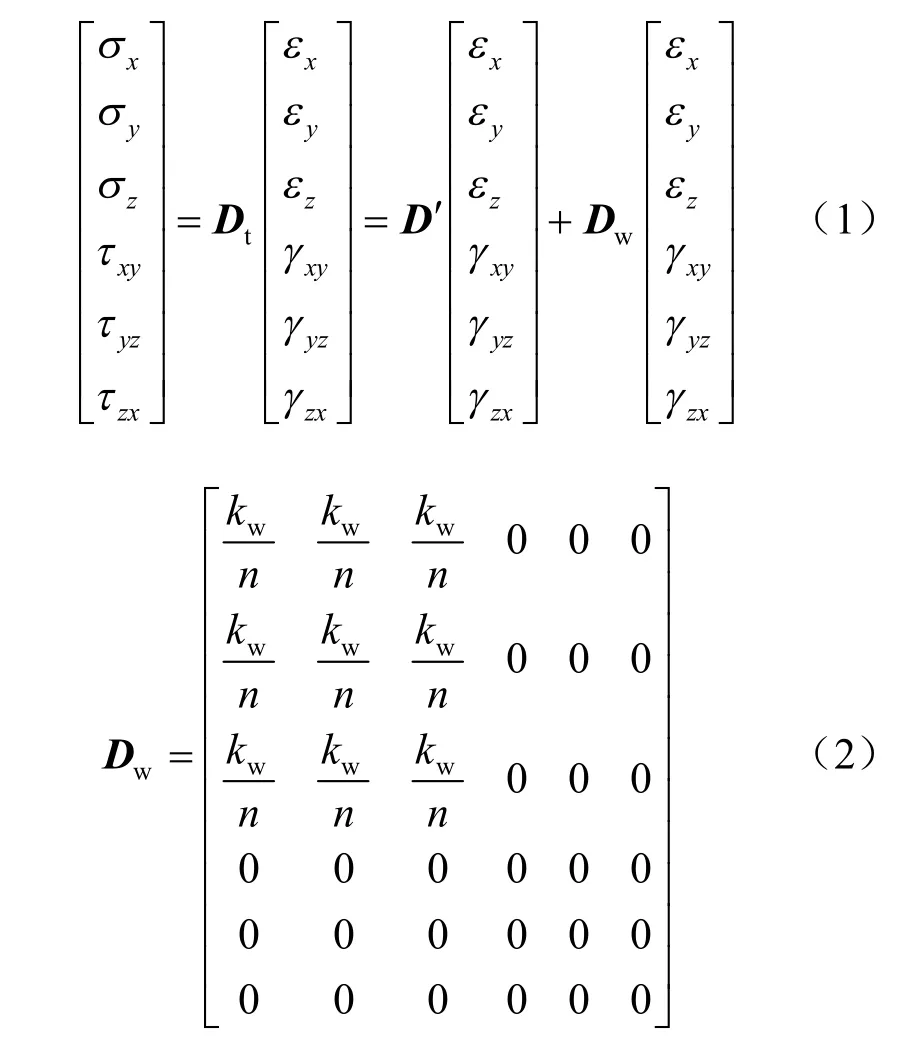
式中:kw为孔隙水的体积弹性模量,一般取值为2.2 GPa;n为土的孔隙率。
根据上述公式推导出孔隙水压力公式,如式(3)所示。采用Abaqus/Explicit 进行分析时,需要进行地应力平衡,使得初始应变为0,即土体和孔隙水自重未引起应变。计算中得到的应变是由外荷载引起的,因此,式(3)的孔隙水压力即为超孔隙水压力。

2.4 荷载及计算参数
套管振动贯入的激振力采用力控制模拟,其中静态荷载 F0=85.5 kN,动力荷载幅值Fc=1 250 kN,
振动频率f=25 Hz,激振力 Fd=F0+Fcsin(2 πf t)。
因只研究机制性状,采用均质土层,土体有限元部分采用 Mohr-Coulomb 弹塑性模型。由于Abaqus/Explicit 采用总应力分析方法,土体参数选用不排水指标,具体参数见表1。

表1 土体参数Table 1 Soil parameters
对于套管壁与土的接触面摩擦角δ 的取值,Potyondy[16]和Acer 等[17]的研究表明,对于黏土,取δ /φ′=0.6~0.7 是比较合适的。黏土有效内摩擦角范围φ′=20°~32°[18-19],则δ=12°~22°,即接触面摩擦系数μ=tanδ=0.2~0.4,取摩擦系数μ=0.25。
套管高频振动贯入过程中振动波受土体阻尼的影响。土体阻尼越低,振动波衰减得越慢。Abaqus中的瑞利材料阻尼包含两个参数:质量比例阻尼 αβ是关于质量矩阵的比例系数,主要用于模拟模型在静态的黏性流体中移动,或用于计算模型绝对运动引起的阻尼力;刚度比例阻尼 βR是关于刚度矩阵的比例系数,主要用于计算应变率引起的阻尼力。由于土体有限元区域施加了边界约束条件,不会产生绝对运动。因此,有限元模型只考虑刚度比例阻尼βR,其表达式为

式中:ξ为阻尼系数;ω1为第一阶固有频率。
采用Abaqus/Standard 提取模型地基的固有频率,其中第一阶固有频率为1.26 Hz。阻尼系数选用Ekanayake 等[20]的推荐值ξ=2%。根据式(4)计算刚度比例阻尼βR为0.032。
3 数值模拟结果与分析
3.1 挤土位移
图4为套管贯入过程中地表水平向位移随径向距离的变化,图中表明:(1)挤土效应引起的水平位移在10D 范围内较明显,且随径向距离增大呈指数型式迅速减小;(2)随贯入深度的增加,地表水平位移稍有增加,这是套管高频振动贯入过程中产生的振动波对地表土体持续作用的缘故[20]。
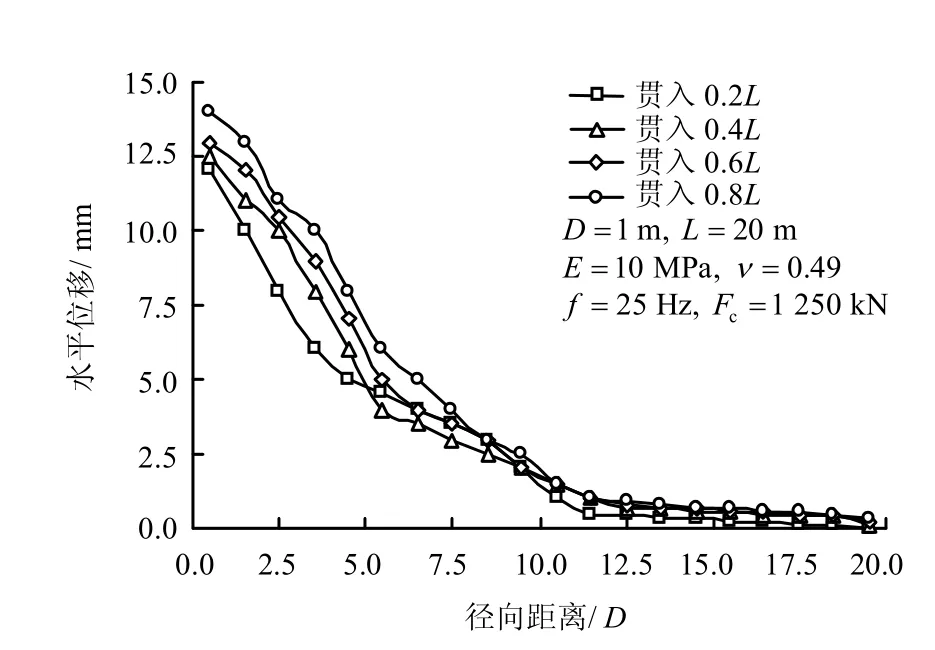
图4 地表水平位移随径向距离的变化Fig.4 Variation of horizontal displacement of ground surface with radial distance
图5为套管贯入过程中地表竖向位移随径向距离(距套管中心距离)的变化,图中表明:(1)套管贯入过程中,套管的拖带效应导致管壁周围出现沉陷区,浅层土体与管壁之间出现脱离,形成深约8 mm 的孔缝,降低套管侧摩阻力,与文献[7]的试验结果相符;(2)最大地表竖向位移出现于径向距离1.5D 处,此范围以外竖向位移逐渐减小,影响范围为10D;(3)地表竖向位移主要发生于套管浅层贯入时,由于上覆土压力的作用,套管深层贯入时地表隆起量基本保持不变。
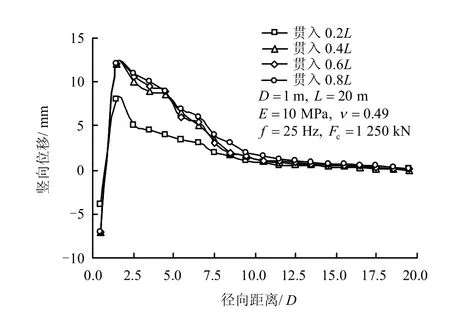
图5 地表竖向位移随径向距离的变化Fig.5 Variation of vertical displacement of ground surface with radial distance
图6为套管贯入过程中径向距离1.5D处土体的水平位移变化规律,图中深度归一化的0 代表地表,1 代表深度为L 的土层。图中可看出,水平位移变化规律为表层、深层土体位移较小,而中部土体位移较大。表层土体水平位移较小是由于地表无约束,套管贯入的侧向挤土位移会由水平变为地表隆起的缘故;由于上覆土压力的作用使中部土体水平位移变大;套管高频振动贯入过程中,振动锤施加在套管顶部的振动能量使土体产生挤土位移,并以振动波的形式向深层传递[21],因物质阻尼和几何阻尼的存在,振动波能量随深度的增大而衰减,导致深层土体位移逐渐减小。
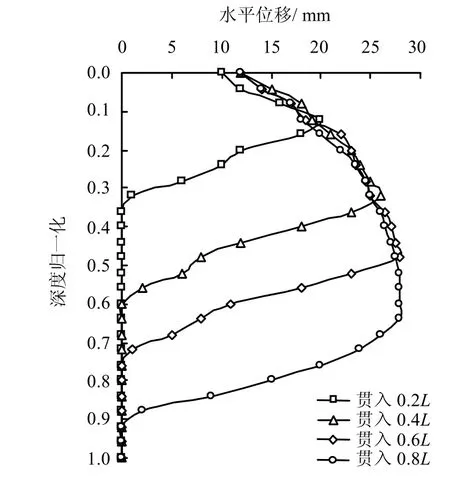
图6 水平位移随深度的变化Fig.6 Variation of horizontal displacement with depth
由图6 还可看出,管端处土体水平位移并未达到最大值,而是管端以上约2D 处土体水平位移达到最大值,且在深层贯入时基本保持不变。随着套管继续贯入,土体发生回弹,上部土体位移稍有减小。由于某一位置的最大挤土位移与套管的贯入深度存在累积效应,若周边有需要保护的管线时,不要误认为只要套管贯入达到管线埋置深度时不产生破坏就安全了,要重视随后超过管线埋置深度的贯入过程对其产生的破坏更大。
图7为套管贯入过程中径向距离1.5D处土体的竖向位移变化规律,正位移代表隆起,负位移代表下沉。图中可看出:(1)浅层土体(0~4D)呈现为地表隆起,深层土体(4~20D)表现为竖向的压缩变形;(2)随着套管贯入深度的增大,浅层土的隆起量增大,而深层土的下沉量增大;(3)竖向位移和水平位移的最大值变化规律一样,管端处土体竖向位移并未达到最大值,而是管端以上约2D 处土体竖向位移达到最大值,且在深层贯入时基本保持不变。
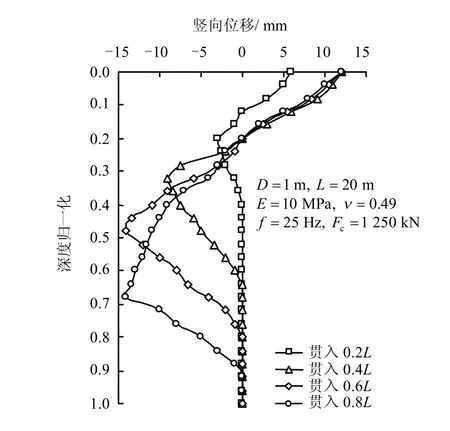
图7 竖向位移随深度的变化Fig.7 Variation of vertical displacement with depth
套管贯入过程中浅层土体的隆起本质上是土体应力场的改变。套管贯入前土体初始应力场如图8(a)所示,其竖向应力和径向应力的大小表示为

式中:γ为土的重度;h为土体深度;k0为静止土压力系数。
套管贯入过程中扩孔挤土应力和振动波使径向应力增加Δσ3,导致竖向产生应力增量Δσ1如图8(b)所示。当应力增量Δσ1大于上覆土体自重σ1时,则土体将向上隆起;相反,如果应力增量Δσ1小于上覆土体自重σ1时,则土体将产生径向位移。
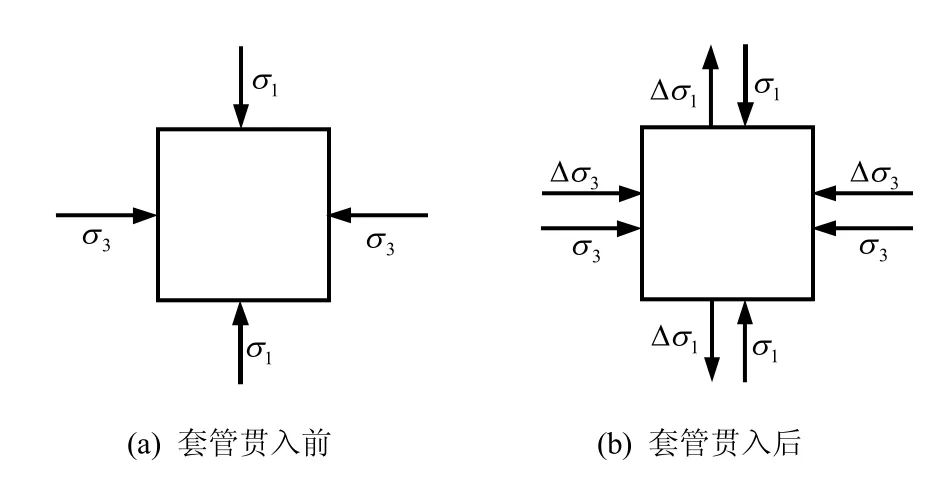
图8 土体应力分布Fig.8 Stress distribution of soils
图9为浅层土体的隆起分界面,表明:(1)在径向距离0.5~0.8D 范围内,套管与土接触面拖带效应导致土体下沉(见图5),该范围土体隆起分界面深度为0;(2)在径向距离0.8~1.5D 范围内,拖带效应对土体影响减小,隆起分界面深度逐渐增大;(3)在径向距离1.5~20D 范围内,随着径向距离增加,隆起分界面深度逐渐减小,且在径向距离10D处隆起量为0.18 m,小于工程管线的最小覆土深度。因此,套管高频振动贯入施工对工程管线的影响半径约可取为10D。
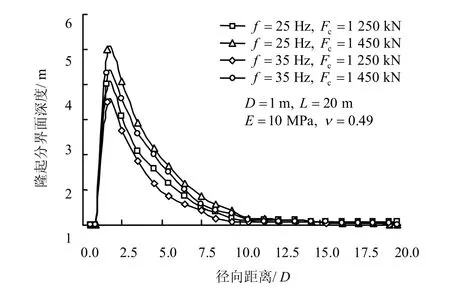
图9 浅层土体的隆起分界面Fig.9 Heave interface of shallow soil
从图9 还可看出:(1)隆起分界面深度随着动力荷载幅值Fc增大而增大。分析认为,振动锤的振动能量由静态荷载F0和动力荷载幅值Fc控制。在F0不变的情况下,增大Fc,径向传播的振动波能量增大,使得径向应力增量Δσ3增加,竖向应力增量Δσ1也相应增加,导致隆起分界面深度增加;(2)隆起分界面深度随振动频率f 的增大而减小。这是由于振动频率越大,振动波能量越小导致的[22]。
因此,若套管贯入处10D 范围内有需要保护的工程管线时,可通过提高振动锤的振动频率或降低动力荷载幅值,从而减小隆起分界面深度,避免工程事故的发生。
3.2 超孔隙水压力
图10为套管贯入过程中径向距离1.5D 处超孔隙水压力变化规律。由图可看出:(1)超孔隙水压力随着贯入深度增加而逐渐增大,贯入到0.8L 时出现最大超孔隙水压力;(2)超孔隙水压力和挤土位移的峰值变化规律不一样,管端处超孔隙水压力处于峰值状态。分析其原因,管端下某一标高的土体随着套管的贯入受到越来越大的挤压,到管端穿过该标高后该处土体主要不再受挤压,而是套管壁与土体的摩擦剪切;(3)浅层土体中超孔隙水压力出现负值情况,随着套管继续贯入,负孔压逐渐趋于0。分析认为,套管贯入时不同深度处的土体位移方向不同。深层土体主要产生水平位移,而浅层土体除了水平位移还产生了竖向隆起,形成较好的排水条件;(4)套管贯入到一定深度时,超孔隙水压力沿深度方向先从负值状态逐渐消散到0,而后逐渐增加到峰值状态(管端处),而后在2~3D 后消散到0,即管端下超孔隙水压力影响范围是2~3D。实际上,超孔隙水压力的变化是由于套管高频振动贯入对周围土体的挤土位移以及循环变化的振动波对周围土体的反复剪切扰动引起的,而后者是十分重要的因素。
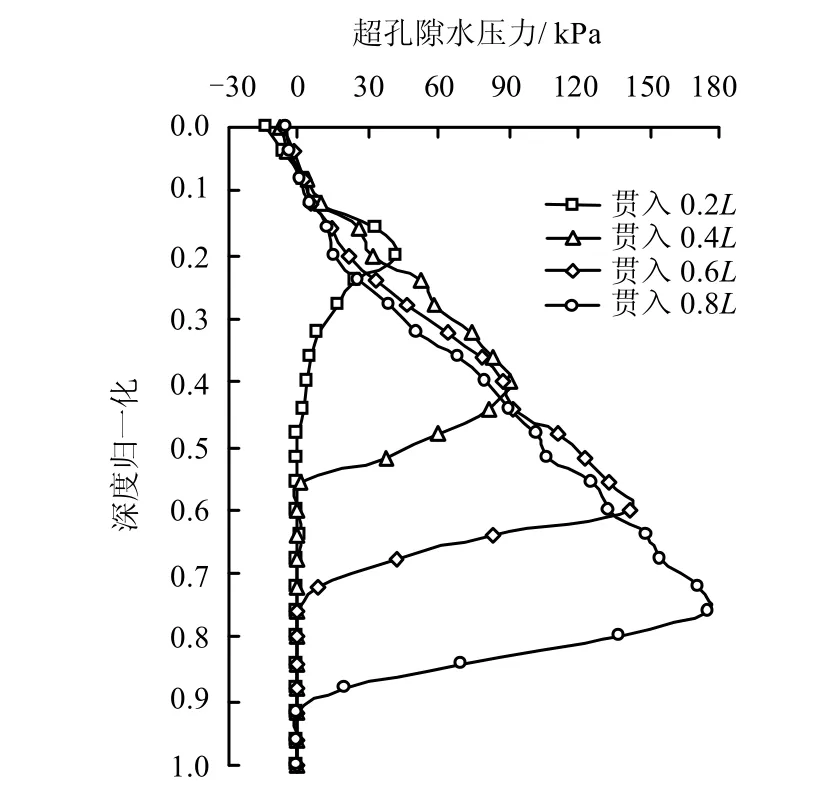
图10 超孔隙水压力随深度的变化Fig.10 Variation of excess pore pressure with depth
由挤土位移沿深度分布特征(如图6、7 所示)和超孔隙水压力沿深度分布特征(如图10 所示)比较发现,两者的变化规律十分接近。这说明挤土位移和超孔隙水压力是相互关联的,是同一物理本质(挤土效应)的两种不同表现。
图11为超孔隙水压力峰值Δumax与上覆有效土压力的比值与径向距离的关系。通过与国内外试验结果[7,23-24]对比发现,数值模拟与试验结果数据虽然具有一定的离散性,但基本位于一条对数型分布的带状区域内,说明超孔隙水压力随径向距离大致呈对数型衰减。数据点的离散性主要源于不同的桩身壁厚、土性和沉桩方式。
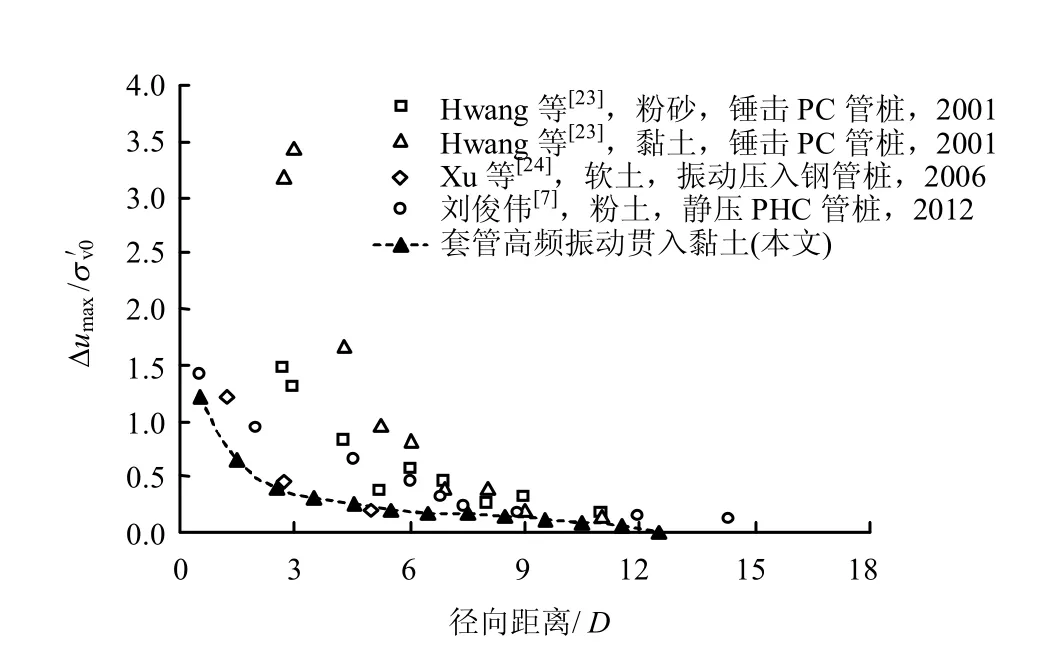
图11 归一化的超孔隙水压力随径向距离的变化Fig.11 Variation of normalized excess pore pressure with radial distance
本文数值模拟的数据点位于带状区域的下部,比其他试验结果较小。桩身壁厚是原因之一,本文采用的套管壁厚为1.5 cm,刘俊伟[7]采用的PHC 管桩壁厚为11 cm,Xu 等[24]采用的钢管桩为13.8 cm,因此,套管的挤土量相比PHC 管桩和钢管桩要小很多,对周围土体挤土效应较小。沉桩方式则为另一原因,套管高频振动贯入过程中,套管壁将周期性的振动荷载传递于套管周围土体[20]。套管下沉时土体产生弹性变形和塑性变形,而回弹时以弹性变形为主。由于在加载过程中土体会产生弹性变形和塑性变形且以塑性变形为主,而卸载过程中主要产生弹性变形,造成土体的滞回特性不对称。如此周而复始,土体的应力-应变滞回曲线逐渐向应变增大的方向移动,破坏了土体的结构强度[25]。套管周围土体在高频振动荷载作用下,应变不断增大,其抗剪强度逐渐减弱,导致套管下沉。而静压沉桩和锤击沉桩法主要是通过挤压桩侧土体,致使桩体下沉。由于采用高频振动贯入法可使套管与土体的相互摩阻力显著降低,克服采用静压贯入和锤击贯入时难以避免的挤土问题,因此,产生的超孔隙水压力也会相应较小。
由图11 还可看出,当径向距离小于10D 时,超孔隙水压力随径向距离增长的变化比较大;当径向距离超过10D 时,超孔隙水压力随径向距离增长的变化逐渐减缓趋于均速。
4 结 论
(1)套管贯入过程中,水平向的挤土位移随套管贯入深度的增加而增大,竖向挤土位移随着贯入深度的增加浅层土表现为隆起量增大,而深层土表现为下沉量增大。
(2)最大挤土位移与套管贯入深度存在累积效应。管端处土体挤土位移并未达到最大值,而是管端以上约2 倍管径处土体挤土位移达到最大值,且在深层贯入时基本保持不变。
(3)浅层土体的隆起为水平应力加载引起竖向应力增加所致,且隆起分界面深度随着动力荷载幅值Fc增大而增大,随振动频率f 的增大而减小。
(4)超孔隙水压力随贯入深度增加而增大,超孔隙水压力峰值位于管端处;超孔隙水压力随径向距离增大呈指数型衰减。
(5)套管高频振动贯入过程中挤土效应的影响范围为10 倍管径,在此范围内有比较重要的管线时,要采取相应的保护措施。
[1]肖勇杰,许万强,陈福全.全套管大直径振动取土灌注桩施工新技术[J].施工技术,2015,44(1):61-64.XIAO Yong-jie,XU Wan-qiang,CHEN Fu-quan.A new construction technology of large diameter cast-in-place piles with sleeves driven by vibratory hammers[J].Construction Technology,2015,44(1):61-64.
[2]雷华阳,李肖,陆培毅,等.管桩挤土效应的现场试验和数值模拟[J].岩土力学,2012,33(4):1006-1012.LEI Hua-yang,LI Xiao,LU Pei-yi,et al.Field test and numerical simulation of squeezing effect of pipe pile[J].Rock and Soil Mechanics,2012,33(4):1006-1012.
[3]聂庆科,胡建敏,商卫东.深厚软土地基上振动沉拔钢护筒对周围土体扰动影响的研究[J].岩土工程学报,2008,30(1):128-132.NIE Qing-ke,HU Jian-min,SHANG Wei-dong.Disturbance effect on soft clay foundation due to steel tube driving by use of shaking method[J].Chinese Journal of Geotechnical Engineering,2008,30(1):128-132.
[4]YU H S.Cavity expansion theory and its application to the analysis of pressuremeters[D].Oxford:University of Oxford,1990.
[5]SALGADO R,RANDOLPH M.Analysis of cavity expansion in sand[J].International Journal of Geomechanics,2001,1(2):175-192.
[6]YI J T,ZHAO B,LI Y P,et al.Post-installation pore-pressure changes around spudcan and long-term spudcan behaviour in soft clay[J].Computers and Geotechnics,2014(56):133-147.
[7]刘俊伟.静压开口混凝土管桩施工效应试验及理论研究[D].杭州:浙江大学,2012.LIU Jun-wei.Experimental and theoretical studies on the construction effects for jacked open-ended concrete pipe piles[D].Hangzhou:Zhejiang University,2012.
[8]刘汉龙,郝小员,费康,等.振动沉模大直径现浇薄壁管桩技术及其应用(Ⅱ):工程应用与试验[J].岩土力学,2003,24(3):372-375.LIU Han-long,HAO Xiao-yuan,FEI Kang,et al.Field pour concrete thin wall cased pile technology ans its application(Ⅱ):Application and in-situ test[J].Rock and Soil Mechanics,2003,24(3):372-375.
[9]黄茂生.深厚软土地基上沉拔钢护筒机制研究[D].北京:北京交通大学,2008.HUANG Mao-sheng.The mechanism research on soft clay foundation due to steel tube driving by shaking method[D].Beijing:Beijing Jiaotong University,2008.
[10]HENKE S,GRABE J.Numerical studies of soil plugging in profiles with open cross-section with respect to the installation method[J].Bautechnik,2008,85(8):521-529.
[11]HENKE S,GRABE J.Numerical investigation of soil plugging inside open-ended piles with respect to the installation method[J].Acta Geotechnica,2008(3):215-223.
[12]MABSOUT M E,TASSOULAS J L.A finite element model for the simulation of pile driving[J].International Journal for Numerical Methods in Engineering,1994,37(2):257-278.
[13]YI J T,LEE F H,GOH S H,et al.Eulerian finite element analysis of excess pore pressure generated by spudcan installation into soft clay[J].Computers and Geotechnics,2012(42):157-170.
[14]YI J T,LEE F H,GOH S H,et al.Effective-stress finite element analysis of spudcan penetration[C]//ASME 31st International Conference on Ocean,Offshore and Arctic Engineering.US:American Society of Mechanical Engineers,2012:87-94.
[15]YI J,GOH S,LEE F,et al.A numerical study of cone penetration in fine-grained soils allowing for consolidation effects[J].Geotechnique,2012,62(8):707-719.
[16]POTYONDY J G.Skin friction between various soils and construction materials[J].Geotechnique,1961,11(4):339-353.
[17]ACER Y,DURGUNOGLU H,TUMAY M.Interface properties of sands[J].Journal of the Geotechnical Engineering Division,1982,108(4):648-654.
[18]李广信.高等土力学[M].北京:清华大学出版社,2004:143-156.LI Guang-xin.Advanced soil mechanics[M].Beijing:Tsinghua University Press,2004:143-156.
[19]常士骠,张苏民.工程地质手册[M].北京:中国建筑工业出版社,2007:156-162.CHANG Shi-piao,ZHANG Su-min.Manual of engineering geology[M].Beijing:China Architecture &Building Press,2007:156-162.
[20]EKANAYAKE S,LIYANAPATHIRANA D,LEO C.Influence zone around a closed-ended pile during vibratory driving[J].Soil Dynamics and Earthquake Engineering,2013(53):26-36.
[21]KHOUBANI A,AHMADI M M.Numerical study of ground vibration due to impact pile driving[J].Proceedings of the ICE-Geotechnical Engineering,2012,167(1):28-39.
[22]MAHUTKA K,GRABE J.Numerical prediction of settlements and vibrations due to vibratory pile driving using a continuum model[C]//International Symposium on Vibratory Pile Driving and Deep Soil Vibratory Compaction.Paris:[s.n.],2006:243-252.
[23]HWANG J H,LIANG N,CHEN C H.Ground response during pile driving[J].Journal of Geotechnical and Geoenvironmental Engineering,2001,127(11):939-949.
[24]XU X,LIU H,LEHANE B M.Pipe pile installation effects in soft clay[J].Geotechnical Engineering,2006,159(4):285-296.
[25]VANDEN J F.Sand strength degradation within the framework of vibratory pile driving[D].Louvain:Université Catolique de Louvain,2001.
