两类运算图的Merrifield-Simmons指标

陈妹君，田双亮

(西北民族大学数学与计算机科学学院，甘肃 兰州 730030)

Merrifield-Simmons 拓扑指标是化学分子图论研究中比较流行和重要的拓扑指标之一，最早是由美国化学家Richard E Merrifield 和Howard E Simmons 在文献［1］中应用有限拓扑阐述化学分子结构理论时提出的.在此基础上，文献［2］对该指标做了进一步研究，并验证了这个有限拓扑的开集数等于点独立集数，并用符号σ 表示.但这个指标的名称一直没有确定下来，直到Gutman 在文献［3］中第一次用Merrifield -Simmons 来命名这个拓扑指标，并且得到了认可.有关Merrifield-Simmons 指标的应用及最新的研究成果在参考文献［4-6］中有详细阐述.本文讨论广义字典积P3［Pm］(如图1)与P3［Cm］(如图2)的Merrifield-Simmons 指标，并给出一种计算公式.

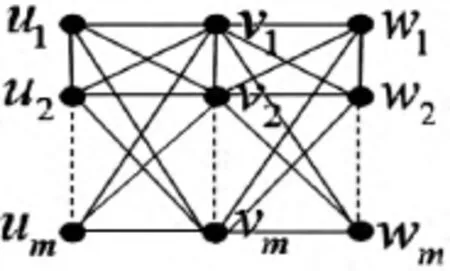
图1 广义字典积P3［Pm］

图2 广义字典积P3［Cm］

1 基本概念和引理

文中所考虑的图G 都是有限无向的简单图.用V(G)、E(G)分别表示图G 的顶点集与边集.

定义1［7］设G 是具有顶点集V(G)= {t0，t1，…，tn－1}(n ≥2)的图，hn= (Hi)i={0，1，…，n－1}是不相交图的序列，其中Hi的顶点集为V(Hi)={(ti，y1)，…，(ti，yx)}，x ≥1．称G［hn］为G 与hn= (Hi)i={0，1，…，n－1}的广义字典积，其中G［hn］的顶点集为，且两个顶点(ti，yp)与(tj，yq)相邻当且仅当ti= tj且(ti，yp)(tj，yq)∈E(Hi)，或(ti，tj)∈E(G).若Hi≅H，i= 0，1，…，n－1 ，则将G［hn］记为G［H］且称G［H］为G 与H 的字典积.

定义2［8］设G 是一个图，v 是图G 的任意一个顶点，则称

是v 的相邻顶点集，称

是v 的闭邻集.

引理1［8］设G 是一个图，对图G 的任意一个顶点v，则有

σ(G)= σ(G － u)+ σ(G － NG［u］).

引理2［8］若G1，G2，…，Gt是图G 的连通分支，则有

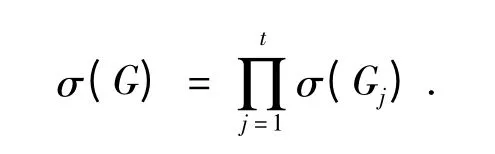
设Fn是Fibonacci 数，其定义为F0= 0，F1=1，n ≥2 时，Fn= Fn－1+ Fn－2，则有以下引理:

引理3［8］设Pn为n 阶的路，则有

引理4［8］设Cn为n 阶的圈，则有

2 主要结论及证明

定理1 当m ≥4 时，

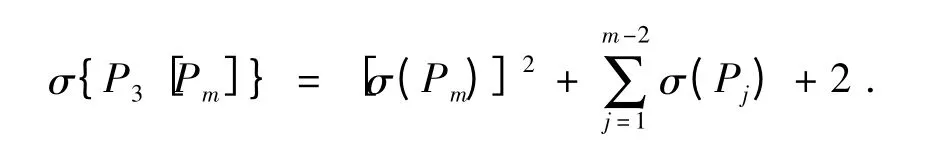
证明 对m 用数学归纳法.

1)当m = 4 时，P3［Pm］= P3［P4］，如图3所示.

图3 P3［P4］

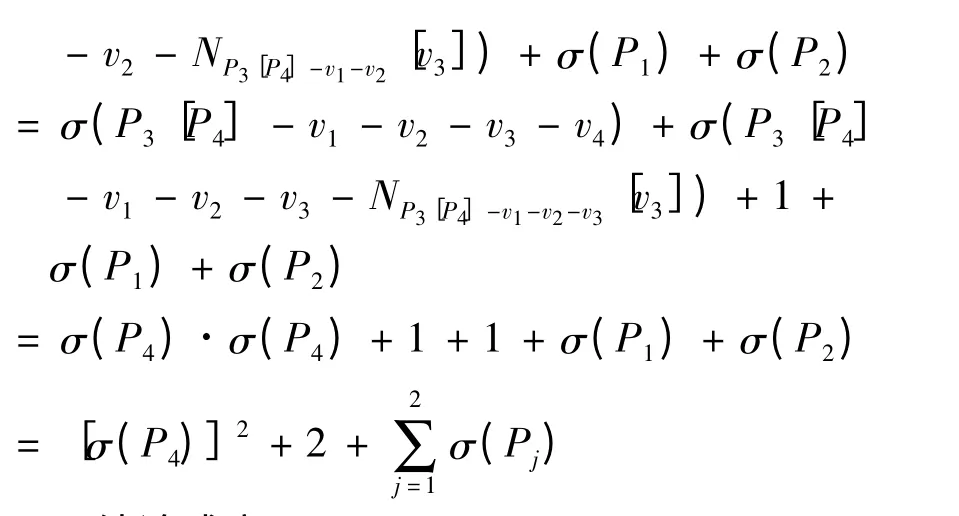
结论成立.

2)假设当m = k －1 时，有

3)当m = k 时，

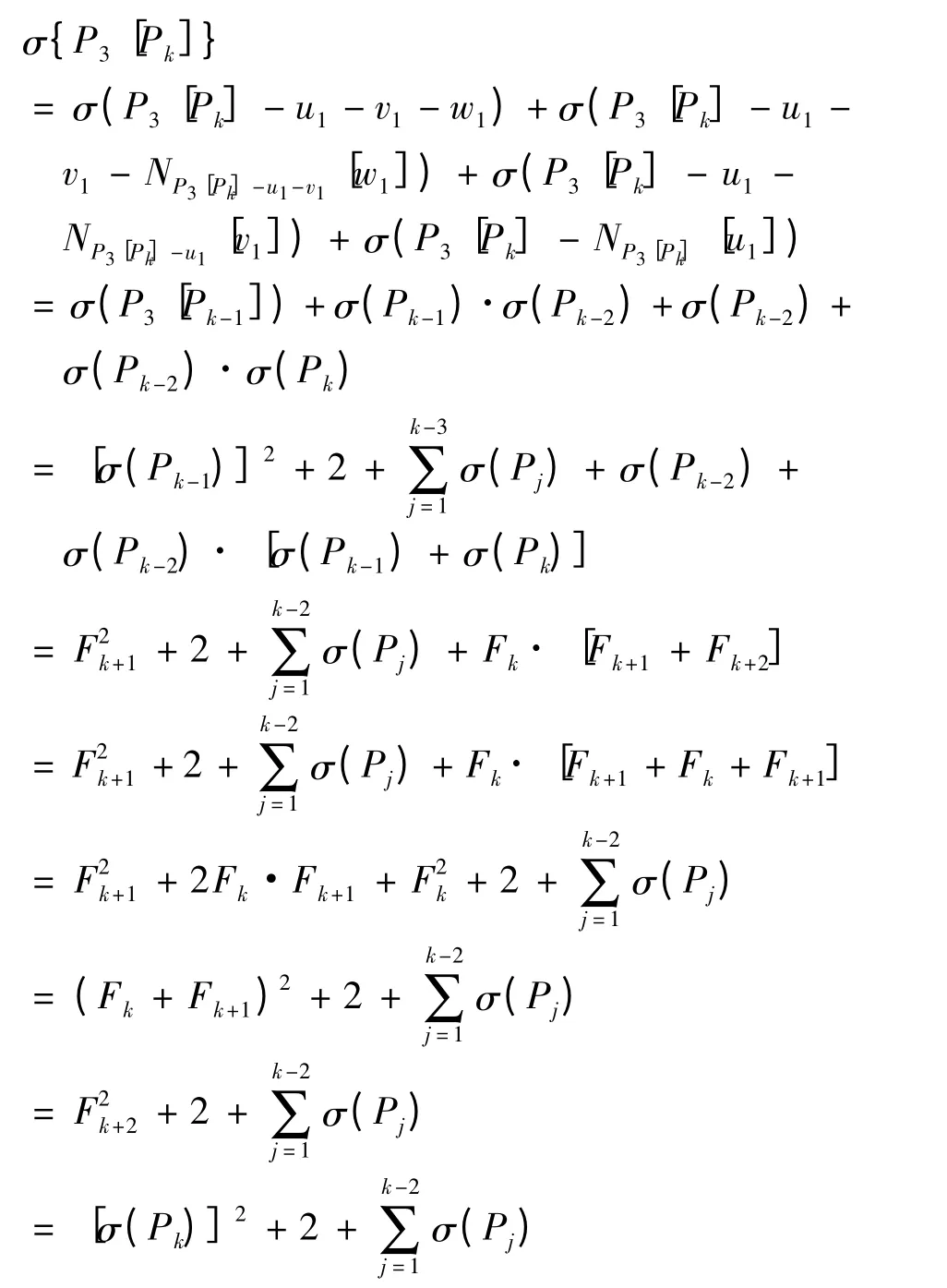
综上所述，当m ≥4 时，有

定理2 当m ≥4 时，

证明 由引理1 和定理1 可知:

［1］Merrifield R E，Simmons H E.The structures of mole cular topological spaces［J］.Theoretica Chimica Acta，1980，55(1):55 -75.

［2］Merrifield R E，Simmons H E.Topological methods in chemistry［M］.New York:Wiley，1989.

［3］Gutman I.Fragmentation formulas for the number of Kekulé structures，Hosoya and Merrifield - Simmons indices and related graph invariants［J］.Coll.Sci.Pap.Fac.Sci.Kragujevac，1990(11):11 -18.

［4］Trinajstic N.Chemical graph theory［M］.Boca Rator，FL:CRC Press，1992.

［5］Deng H Y.The smallest Merrifield -Simmons index of(n，n + 1)- graphs［J］.Mathematical and Computer Modeling，2009，49(1 -2):320 -326.

［6］Xu K X.On the Hosoya index and the Merrifield -Simmons index of graphs with a given clique number［J］.Applied Mathematics Letters，2010，23(4):395-398.

［7］Waldemar S，Iwona W，Andrej W.On the existence and on the number of(k，l)- kernels in the lexicographic product of graphs［J］.Discrete Mathematics，2008，308:4616 -4624.

［8］Gutman I，Polansky O E.Mathematical concepts in organic chemistry［M］.Berlin:Springer，1986.