带有齐次核的多参数Hilbert型不等式的加强

杨玉英

(吉首大学数学与统计学院,湖南 吉首416000)



带有齐次核的多参数Hilbert型不等式的加强

杨玉英

(吉首大学数学与统计学院,湖南 吉首416000)

通过引入权函数，应用实分析的技巧,对全平面上具有齐次核Hilbert型积分不等式作了改进，从而建立了一些新的不等式.

齐次核；权系数；参数；Hilbert型积分；不等式

1 问题的提出

(1)

(2)

笔者的目的是利用改进的Hölder不等式对(2)式进行加强，从而建立一些新的不等式.

2 相关基础知识

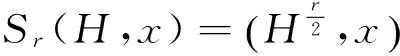
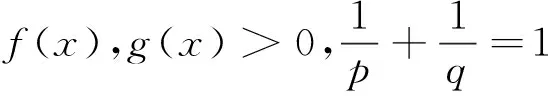
证明见文献[2-3].

引理2若0<α1<α2<π，定义权函数ω(y)和ϖ(x)如下：

证明见文献[1].

3 主要结果及其证明

为方便起见，再引入一些符号：

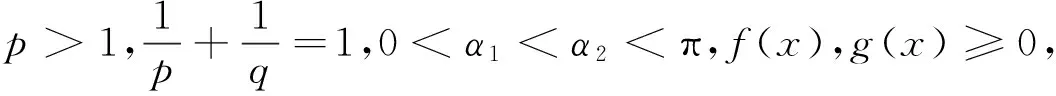
(3)

这里Rλ=(Sp(Fα,h)-Sq(Gα,h))2，而

(4)

证明由引理1和引理2，有

即(3)式成立.

接下来讨论Rα的表达式.选取由(4)式所定义的函数h(x,y)，有

由引理1，得

而

所以

Rα<1.

定理1证毕.

注1(3)式即为(2)式的改进式.

[1] YANG Bicheng.A Hilbert-Type Integral Inequality in the Whole Plane with the Homogeneous Kernel[J].Journal of Mathematical Inequalities,2013,7(2):289-298.

[2] HE Leping,GAO Mingzhe.A Hilbert Integral Inequality with Hurwitz Zeta Function[J].Journal of Mathematical Inequalities,2013,7(3):377-387.

[3] LIU Tuo,YANG Bicheng,HE Leping.On a Half-Discrete Reverse Mulholland-Type Inequality and an Extension[J]. Journal of Inequalities and Applications,2014(1):103.

(责任编辑 向阳洁)

Strengthened Multi-Parameter Hilbert-Type Inequality with Homogeneous Kernel

YANG Yuying

(College of Mathematics and Statistics,Jishou University,Jishou 416000,Hunan China)

By introducing the weight function and using the technique of real analysis,an improvement of Hilbert-type integral inequality with homogeneous kernel in the whole plane is given.Some new inequalities are thus established.

homogeneous kernel;weight coefficient;parameter;Hilbert-type integral；inequality

1007-2985(2015)04-0009-03

2014-09-04

杨玉英(1970—)，女，湖南靖州人，吉首大学数学与统计学院副教授，主要从事代数与几何研究.

O178

A

10.3969/j.issn.1007-2985.2015.04.003