C语言中浮点数精度问题分析

周冠方

（郧阳师范高等专科学校组织人事部，湖北十堰420000）

C语言中浮点数精度问题分析

周冠方

（郧阳师范高等专科学校组织人事部，湖北十堰420000）

通过实例直观地描述了C语言中由于计算机存储数据方式的不同而造成的数据误差，并对误差产生的原因进行了分析，解读出C语言中浮点型数据的不同存储方式，最后给出几点建议。

C语言；数据精度；浮点型数据；相对误差

1 引言

C语言程序设计的基本数据类型包含整型和浮点型两类。在计算机中，实数特别是小数形式表示的数都是以浮点型数据来进行存储的。但是对于浮点型的数据，在进行各种运算时，因为计算机的二进制存储特性，会导致出现精度丢失的现象。这种现象直接影响到程序结果的准确性和可靠性。

2 C语言中数据类型转换带来的影响

先来看一个简单的例子：需要求解A＝4/5的值，这个结果很简单，A＝0.8。而在C语言中，我们写出它的计算程序：

Main（）

｛

Float A；

A＝4/5；

Printf（“A＝%f＼n”，A）；

Return 0；

｝

结果：A＝0.000000

从算法的角度来看这个程序没有问题，但是最终运行的结果却和我们的理论值完全不相符。这是为什么呢？

分析：在此程序中两操作数4和5均为整型，运算结果应该为0.8，但是在C语言程序编写中有这样一个规则，C语言中计算的源数据为整形数据，最终输出结果也应该为整形数据。“4/5”的结果0.8在C语言中会被转换后得到一个int型的中间变量，它的值等于“4/5”的整数部分，其小数部分则被进行截尾操作，即舍弃整个小数部分，最终存储值为0。程序将这个整型的运算结果赋给A这个float型变量，将其强制转换为float型输出，所以最终运算结果成了A＝0.000000。

如果我们需要去确保最终输出结果的正确性，我们就必须在计算的过程中就将中间的操作数据更改为浮点型数据，来确保最终结果数据和中间操作数据的数据类型的同质性。

此例有两种简单的解决办法：

1）将“A＝4/5”改成“A＝4.0/5.0”；

2）将“A＝4/5”改成“A＝（float）4/5”。

即可得出最终正确的值A＝0.800000。因此，如果我们遇到因为C语言程序设计中，不同数据类型之间的计算问题时，我们必须规定明确的数据类型，并且在算法编写的过程中，通过人为的数据类型变更的方法，确保程序计算中过程值和结果值的数据类型的同质性，从而达到保证计算精度准确的目的。

3 C语言中存储位数溢出的控制

同样的例子，我们做一个简单的修改：

Main（）

｛

Float A；

A＝（float）4/5；

Printf（“A＝%10.8f＼n”，A）；

Return 0；

｝

我们将输出结果限定为10位有效数字，小数点后有效数字为8位。程序运行后得到结果为：A＝0.80000001。这显然也不是我们想要的结果：A＝0.80000000。为了知道这个原因，我们就必须了解C语言中浮点类型数据的存储格式要求。

3.1 C语言中浮点类型数据的存储格式

C语言中的浮点数是以IEEE 754标准的格式存储，与整型数据的存储完全不一样。

3.1.1 单精度浮点型数据

C语言中对float型数据（4个字节）的表示分为三个部分：符号S，阶码E，尾数M。具体如下（见表1）：

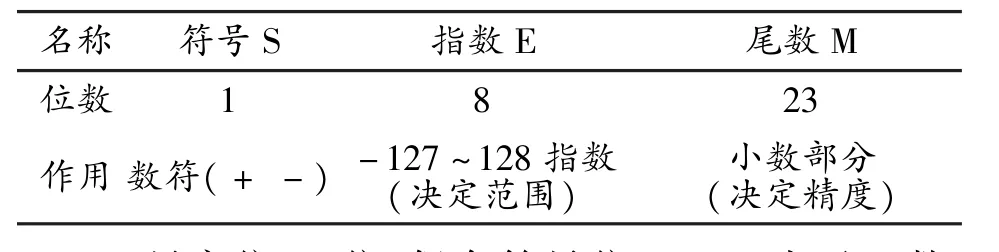
表1 单精度浮点型数据存储格式表

1）最高位31位，保存符号位S，“0”表示正数，“1”表示负数。［1］

2）30位～23位，共8位，移码方式（指数值加上偏移量127）保存指数部分，称为阶码。

3）22位～0位，共23位，保存系数部分，称为尾数，对于规范化二进制数，整数位的前导“1”不保存（隐含），直接保存小数部分b1b2…b23。

实际上即是将十进制数R在计算机中用二进制数的科学计数法表示出来：R＝（－1）S×M×2E。

而在float类型的数据中，它的精度是由尾数的位数来决定的。浮点数在内存中是按科学计数法来存储的，其整数部分始终是一个隐含着的“1”，由于它是不变的，故不能对精度造成影响。

float：2＾23＝8388608，一共七位，106＞8388608＞107这意味着最多能有7位有效数字，但绝对能保证的为6位，即float的精度为6～7位有效数字。因此，当我们用“A＝%10.8f＼n”来控制输出结果的小数位数为8位时，就会出现精度丢失的问题，即多出来了0.00000001。

Float型的一些特殊约定：［2］

2）当E＝0，M！＝0时，表示非规范化数，即r＝（－1）S×2－127×（0.M）；

3）当E＝255，M＝0时，表示无穷大，用符号位来确定是正无穷大还是负无穷大；

4）当 E＝255，M！＝0时，表示 NaN（Not a Number，不是一个数）；

对于Double型，也有相似的约定。

3.1.2 双精度浮点型数据

在控制输出结果的实际位数的时候，我们必须考虑其存储的精度值。因此可以通过提高变量的精度值定义的方式来尽量缩减这种误差。例如，我们将上例改为：

Main（）

通过查阅《中国煤炭工业年鉴2008》统计出1984年至2008年我国煤矿百万吨死亡率数据。根据对国家安全管理监督总局(现改名为中华人民共和国应急管理部)公报的搜集，整理出2009年至2017年我国煤矿百万吨死亡率数据[7，8]。得出我国近30年煤矿百万吨死亡率曲线走势图。如图1所示。

｛

double A；

A＝（float）4/5；

Printf（“A＝%10.8f＼n”，A）；

Return 0；

｝

结果：A＝0.80000000

分析：通过对于变量A的数据类型精度的提高，将其由float变为double，而双精度数据（double）其存储范围则扩大了许多，从32位变为了64位（见表2）。

表2 双精度浮点型数据存储格式表

Double的精度：2＾52＝4503599627370496，一共16位，1015＜4503599627370496＜1016这意味着最多能有16位有效数字，但绝对能保证的为15位，即double的精度为15～16位有效数字。这样就可以保证在指定8位有效数字时的数据的精度。

同理，就算应用双精度，我们也需要注意指定的小数点后有效数位，不能够超出其实际的有效位数。

另外，long double型数能提供的十进制数的有效数字不超过19位，即精度为18～19。但由于C语言没有去充分实现，其实际能提供的数据的精度与double型相当。

3.1.3 设定数据偏移量

我们还可以使用在程序中加设数据偏移量的方法来尽量规避这种由于数据存储类型的限制而造成的误差，假设我们设定数据偏移量为0.001，在printf程序语句前加上下面的控制程序：

if（A－0.800＜0.001∗5）

｛

A＝0.800；

｝

else

｛

A＝0.800＋0.001；｝

通过程序来控制数据的精度，可以得出最终的结果A＝0.80000000。

4 浮点数使用时的另外几种易出现误差的情况

4.1 判断两个经过运算的浮点数相等

由于浮点数是采用二进制科学计数法来进行存储的，因此，绝大多数的小数在计算机内存中是不能精确表示的。

例如：如果两个数x、y都是直接用常数赋值，这时我们判断x，y是否相等。

Main（）

float x＝8.8，y＝8.8；

if（x＝＝y）

｛

printf（＂x＝y＼n＂）；

｝

输出：x＝y

如果我们将x或y改成经过运算后得到的值，这时我们再来判断x，y是否相等：

Main（）

float x＝4.4＋4.4，y＝8.8；

if（x＝＝y）

｛

printf（＂x＝y＼n＂）；

｝

else

｛

printf（＂x！ ＝y＼n＂）；

｝

输出：x！ ＝y从这个例子就可以发现，C语言中浮点数的计算结果很多都是近似到浮点数的最大表示值来处理的，这样一来就会造成误差。因此，如果想判断x是否等于y，应该用两数之差的绝对值和一个很小的数来比较，当差值小于这个很小的数时，我们就可以确定两个数近似相等：fabs（x－y）＜10－6。

4.2 浮点数作为循环变量

C语言中由于浮点数计算存在的误差，可能会使循环次数达不到预定的次数而导致程序出现误差，例如：

main（）

｛

float i j；

for（i＝1，j＝0；i＜ ＝10；i＋ ＝0.1）

｛

j＋ ＝i；

｝

printf（“j＝%f”，j）；

｝

这个程序中，因为i是浮点数计算取得值，会导致在循环到10的时候它的实际内存存储值变成10.000000001，这个值大于10，for语句会使程序循环终止，因此没有达到预定的循环次数，导致求和结果和我们本身想要的结果有误差。

4.3 一个很大的浮点数加上一个比较小的浮点数

C语言中由于浮点数数据存储有效位数的原因，可能会在计算一个很大数加上一个很小的数时，小数计入大数累加时被溢出而造成误差，例如：

Main（）

｛

float i，j，sum；

i＝1000000；j＝0.1

sum＝i＋j；

printf（“sum＝%f＼n”，sum）；

return 0；

｝

因为float一共只有6～7位有效数字（10进制），如果整数部分的位数多了，相应的小数部分的精确显示位数就少了，因此当一个很大的数（如100000）去加一个很小的数（如0.1），那么小数部分的数值就会因为存储溢出而丢失，从而产生误差，得不到我们想要的理论值1000000.1，而是1000000.0。

5 结束语

C语言程序编写时，如果没有很好地理解和掌握数据存储和数据类型转换的问题，那么在实际的编程中就会出现很多的误差。特别是在做浮点型数据计算的过程中，由于内存中存储的方式多为乘2取整，所以计算机在精度范围内取舍时会导致数据出现误差。在实际的编程中一定要注意C语言中浮点型数据的精度问题。

［1］张宗杰，张明亮.C语言中浮点数的存储格式及其有效数字位数［J］.计算机与数字工程，2006（1）：84.

［2］杜叔强.浅析C语言中的浮点数［J］.兰州工业高等专科学校学报，2010（5）：26.

Analysis on Precision of Floating－point Number for C Language

ZHOU Guan⁃fang
（Organizational and Personnel Department，Yunyang Teachers’College，Shiyan 420000，China）

This article describes how data errors are caused in C language due to differentdata storagemethod with case study，an⁃alyses the reason for such errors and explains different storagemethods of floating point data in C language.Finally，some sugges⁃tions are proposed in this article.

C Language；data precision；floating point data；relative error

TP312

A

2095⁃8153（2015）03⁃0097⁃03

2015⁃05⁃15

周冠方（1984－），男，郧阳师范高等专科学校组织人事部助教。