n值逻辑系统中矛盾度的等价定义及性质

李顺琴, 惠小静

(延安大学 数学与计算机科学学院,陕西 延安 716000)



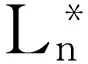
李顺琴, 惠小静

(延安大学 数学与计算机科学学院,陕西 延安 716000)

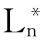
计量逻辑学；R0-命题逻辑系统；矛盾度；等价形式；对称性定理

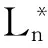
1 预备知识

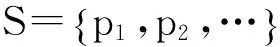
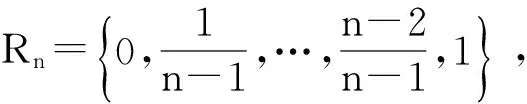
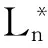
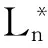
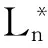
2 公式真度定义的等价形式

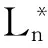
证明结合定义4知，只需证明

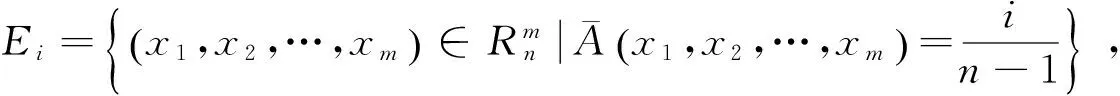
从而

即

所以

结合定义4，得

由定理再结合引理1，可得如下推论：

推论1设A=A(p1,p2,…,pm)∈F(S)，则

(ⅰ)A是重言式当且仅当Cn(A)=0.

(ⅱ)A是矛盾式当且仅当Cn(A)=1.

3 矛盾度的相关性质

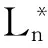
(ⅰ)若A≈B(A～B)，则Cn(A)=Cn(B).

(ⅱ) Cn(A∨B)=Cn(A)+Cn(B)-Cn(A∧B).

(ⅲ) Cn(A)=1-Cn(A).

(ⅳ) 若A→B是定理，则Cn(A)≥Cn(B).

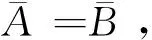
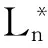
即

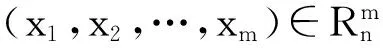
因此

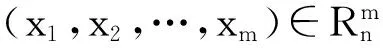
从而

结合定理1，得

Cn(A∨B)=Cn(A)+Cn(B)-Cn(A∧B)

再结合定理1，得

Cn(A)=1-Cn(A).

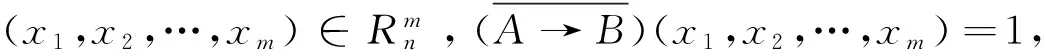
结合定理1，得

Cn(A)≥Cn(B)

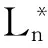
Cn(A1∨A2∨…∨As)

证明对s用数学归纳法证明.

当s=2时，根据定理1(ⅱ)知结论成立.

假设

+(-1)s-2Cn(A1∧A2∧…∧As-1)

那么

Cn(A1∨A2∨…∨As)

=Cn((A1∨A2∨…∨As-1)∨As)

=Cn(A1∨A2∨…∨As-1)+Cn(As)-Cn((A1∨A2∨…∨As-1)∧As)

=Cn(A1∨A2∨…∨As-1)+Cn(As)-Cn((A1∧As)∨…∨(As-1∧As))

根据数学归纳法知结论对s∈Z+-{1}成立.

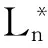
证明设A=A(p1,p2,…,pm)∈F(S)是含有m个原子公式p1,p2,…,pm的命题公式.把A中的原子公式pi换成pi，公式A变成公式B，即

A(p1,…,pi-1,pi,pi+1,…,pm)=B(p1,…,pi-1,pi,pi+1,…,pm)

φ(x1,…,xi-1,xi,xi+1,…,xm)=(x1,…,xi-1,1-xi,xi+1,…,xm)

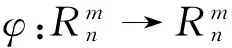
因此

由定理1，知Cn(A)=Cn(B).

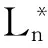
[1] PAVELKA J.On fuzzy logic:I,II,III[J].Z Math Logic Grundlagen Math,1979,25:45-52，119-134，447-464.

[2] 王国俊.数理逻辑引论与归结原理[M].北京:科学出版社,2006.

[3] 王国俊.计量逻辑学(I)[J].工程数学学报,2006,23(2):191-215.

[4] WANG G J,ZHOU H J.Quantitative logic[J].Information Sciences,2009,179(3):226-241.

[5] 李俊,王国俊.逻辑系统Ln中的命题真度理论[J].中国科学(E辑),2006,36(6):631-643.

[6] 王国俊,傅丽,宋建社.二值命题逻辑中命题的真度理论[J].中国科学(A辑),2001,31(11):998-1008.

[7] 王国俊,李壁镜.Lukasiweicz n值逻辑中公式的真度理论和极限定理[J].中国科学(E),2005,35(6):561-569.

[8] 王国俊,宋建设.命题逻辑中的程度化方法[J].电子学报,2006,34(2):252-2571.

[9] 王国俊,高香妮.命题逻辑系统中理论的真度概念及其应用[J].陕西师范大学学报:自然科学版,2009,37(5):1-6.

[10]周建仁,吴洪博.Lukasiewicz命题逻辑系统中真度的等价定义及相关性质[J].工程数学学报，2013,30(4):580-590.

[11]刘华文,王国俊,张诚一.几种逻辑系统中的近似推理理论[J].山东大学学报：理学版,2007,42(7):77-81.

[12]张红杰,吴洪博.n值R0-命题逻辑系统L*n中公式的矛盾度理论[J].云南师范大学学报：自然科学版，2007,27(4):1-7.

An Equivalent Definition and Some Properties of Controdicition Degreees in N-valued Propositional Logic System L*n

LI Shun-Qin, HUI Xiao-Jing

(College of Mathematics and Computer Science,Yan′an University,Yan′an 716000,China)

An intuitionistic equivalent form of the definition of controdicition degrees in n-valued R0-propositional logic system L*nis given,and the proofs of some important properties of controdicition degreees are simplified through the equivalent form of definiton.Moreover, the symmetrical characteristic of controdicition degrees is obtained.

Quantitative logic;R0-proposition logic; Controdicition degree; Equivalent definition; Symmetry theorem

2014-11-18

国家自然科学基金资助项目(11471007)；陕西省自然科学基金资助项目(2014JM1020)；陕西省科技计划资助项目(2014ks15-03-07)；陕西省高水平大学建设专项资金资助项目(2012SXTS07).

李顺琴(1978-)，女，陕西延安人，硕士，讲师，主要从事不确定性推理方面研究.E-mail:lishq_mm@163.com.

李顺琴.

O141.1

A

1007-9793(2015)03-0036-05