不可数空间的可数补拓扑的几类连通性

王小霞, 姜金平, 赵宁宁, 李萍

(延安大学 数学与计算机科学学院,陕西 延安 716000)



不可数空间的可数补拓扑的几类连通性

王小霞, 姜金平, 赵宁宁, 李萍

(延安大学 数学与计算机科学学院,陕西 延安 716000)

讨论了不可数空间的可数补拓扑的θ-连通性、θ-弧连通性和局部道路连通性.

不可数空间; 可数补空间; 连通性

连通性是拓扑空间研究的一个重要课题,文[1]讨论了一般拓扑空间的连通性，文[2]讨论了θ-连通性空间与θ-连通性，文[3]研究了θ-弧连通空间和θ-弧连通性,文[4]讨论了局部道路连通性,文[5]讨论了一类可数补空间的连通性和弧连通性。在文[5]的基础上，讨论了不可数空间的可数补拓扑的θ-连通性、θ-弧连通性和局部道路连通性,进一步完善可数补空间的连通性理论.

1 预备知识

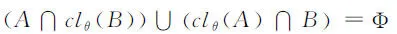
定义3[2]设(X，T)、(Y，ω)为两个拓扑空间,f:X→Y是映射,若∀θ -开集B∈Y,有f-1(B)是X中的θ -开集,则称f为θ-连续映射.

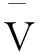
定义5[3]设(X，T)为拓扑空间,若对X中任意两点x、y都有X中θ-连续映射f:[0,1]→X,使得f(0)=x,f(1)=y,则称(X，T)为θ-弧连通空间.

定义6[4]设X为拓扑空间, ∀x∈X,若∀U∈Ux,∃x∈X的道路连通邻域V,使得x∈V⊂U,则称X是局部道路连通空间.

定义7设X为拓扑空间,若X包含不可数多个点,则称X为不可数空间.

2 主要结论

定理1设(X，T)是包含不可数多个点的可数补空间,则X是θ-连通的.

定理2[5]X为可数集,T={X-C:C为可数集}∪{Φ},则(X，T)为离散空间.

定理3如果Y为不少于两点的离散空间,则拓扑空间X为θ-连通空间当且仅当有一θ-连续映射f:X→Y都是常值映射.

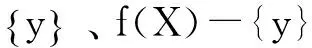
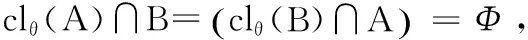
定理4设(X，T)是包含不可数多个点的可数补空间,则X不是θ-弧连通空间.

证明∀x、y∈X,且x≠y,假设x、y是θ-弧连通的,由文[3]定义1.1知存在θ-连续映射f:[0,1]→X，使得f(0)=x,f(1)=y,由于[0,1]是不可数集,则f([0,1])也是不可数集.

事实上,若f([0,1])是可数集,且至少含两点x、y,令Y=f([0,1]),由文[5]引理1知(Y,T|Y)为离散空间,且f|Y:[0,1]→Y为满射,且为θ-连续映射,因为[0,1]是连通的,从而是θ-连通的,由文[2]定理4.8知f([0,1])是θ-连通的,由本文定理3知f([0,1])=Y为独点集,矛盾.

令B={x|x∈I,x为有理数}⊂[0,1],则B为可数集,由文[1]定理1.7.2知f(B)为可数集.因为f(B)⊂f([0,1]),而f([0,1])为不可数集,所以∃t∈[0,1],使f(t)∈f([0,1]),但f(t)∉f(B),故t必为无理数,令C=X-f(B)，则C为X中θ-开集且f(t)∈C,所以f-1(C)为[0,1]中θ-开集,且t∈f-1(C),因为f-1(f(B))⊃B,所以f-1(C)=f-1(X)-f-1(f(B))=[0,1]-f-1(f(B))⊂[0,1]-B，而[0,1]-B为[0,1]中无理数集,它的任意非空子集均不是θ-开集,这与f-1(C)为θ-开集矛盾,从而x、y不是θ-弧连通的,故X不是θ-弧连通空间.

定理5[1]可数补空间是局部连通空间.

定理6设(X，T)是包含不可数多个点的可数补空间,则X不是局部道路连通空间.

证明假设X是局部道路连通空间,则由文[4]定义2可知∀x∈X,∀U∈Ux,∃x的道路连通邻域V,使得x∈V⊂U.从而V为道路连通的,设y,z∈V,且y≠z,即y,z是道路连通的,由道路连通定义,存在连续映射f:[0,1]→X,使f(0)=x,f(1)=y,记I=[0,1],因为I不是可数集,类似于定理2,同理可证f(I)也是不可数集.

令B={x|x∈I,x为有理数}⊂I,则B为可数集，由文[1]定理1.7.2知f(B)为可数集，类似于本文定理2，可知I-B为I中无理数集, 它的任意非空子集均不是开集,这与f-1(C)为开集矛盾!故x、y不是道路连通的,故V不是道路连通子集,即∀x∈X,∀U∈Ux,不存在X的道路连通邻域V,使x∈V⊂U,从而与假设矛盾!故X不是局部道路连通空间.

[1] 熊金城.点集拓扑讲义[M].北京：高等教育出版社,1997.

[2] 许兆龙.θ-连通空间与θ-连通[J].韶关学院学报：自然科学版,2002,23(6):17-24.

[3] 许兆龙.θ-弧连通空间与θ-弧连通[J].抚州师专学报,2003,22(3):46-49.

[4] 张喜贵.局部道路连通空间[J].通化师范学院学报,2002,23(5):14-17.

[5] 陈燕芬.一类可数补拓扑空间的连通性与弧连通性[J].韩山师范学院学报：自然科学版，1996 (3):27-29.

Several Connectedness of Countable RemainderTopological Spaces of Uncountable Spaces

WANG Xiao-xia, JIANG Jin-ping, ZHAO Ning-ning, LI Ping

(College of Mathematics and Computer Science,Yan′an University，Yan′an 716000，China)

This article discusses the θ-connectedness, θ-arcwise connectedness and local path connectedness in countable remainder topological spaces of uncountable spaces.

Uncountable spaces;Countable remainder topological spaces; Connectedness

2014-10-29

陕西省科技厅科研基金资助项目(2014k15-03-07，2014JM2-1005)；陕西省教育厅科研基金资助项目(15JK1832);延安市科技计划基金资助项目(2012ks-01)；陕西省大学生创新创业训练计划资助项目(1066).

王小霞(1978-)，陕西商洛人，副教授，硕士生导师，主要从事格上拓扑学方面研究.

姜金平(1974-)，陕西洛川人，博士，副教授，硕士生导师，主要从事模糊拓扑与计算数学方面研究.

O189.1

A

1007-9793(2015)03-0033-03