改进的主动土压力计算方法

王仕传，孙本杰，邵 艳

（安徽建筑大学 土木工程学院，安徽 合肥 230601）

1 引言

土压力分布和挡土墙位移模式、位移大小密切相关。Terzaghi[1－2]通过模型试验指出，墙后土压力分布为非线性。Sherif[3]、Fang[4]等对不同位移模式下砂土的土压力试验研究表明，墙体位移模式和位移大小对土压力分布的影响很大。周应英等[5]对砂土在平动位移模式、黏土在绕墙底和绕墙顶转动位移模式下刚性挡土墙主动土压力分布进行了室内试验研究，也证实了墙后土压力分布和挡土墙位移模式、位移大小相关。建立在极限平衡状态基础上的经典土压力理论不能反映挡土墙位移大小和位移模式等因素的影响。基于水平层分析法的极限平衡状态土压力计算理论能反映位移模式的影响，但实际挡土墙位移大小都是有限的，墙后填土很难达到极限平衡状态，大多为非极限平衡状态。

对于非极限状态土压力计算，通常采用两种方法[6]：一是用函数拟合土压力随位移变化的关系曲线；二是采用非极限状态下摩擦角参数替换经典土压力理论的极限摩擦角，即采用了土的抗剪强度发挥值的概念，能够反映位移变化对墙后土体应力状态的影响。文献[7]针对平动模式下的刚性挡土墙，建立了内外摩擦角与位移之间的关系式，分析了最不利情况下墙后土楔体的受力情况，得到考虑位移效应的非极限土压力公式。文献[8]基于朗肯土压力基本原理，假定填土内摩擦角与该点土体位移呈非线性关系，提出考虑位移影响的主、被动土压力计算公式。文献[9]利用卸荷路径三轴试验中径向应力和应变间较好的双曲线关系[10]，建立非极限状态摩擦角和挡墙位移的关系，并求得平动位移模式下无黏性土挡土墙任意位移时的墙后土压力非线性分布解。文献[6]在文献[9]的基础上，从黏性土的应力摩尔圆出发，建立了黏性土的抗剪强度参数随位移变化的关系式，运用水平微分单元法推导出非极限状态平动模式时黏性土的主动土压力计算公式。考虑位移影响的土压力计算方法还有有限单元法[11－12]，但有限元法涉及到填土的本构模型研究及参数选取，还有墙-土间的接触面处理及参数确定等问题，不利于工程应用。

针对绕墙底向外转动的重力式挡土墙，本文基于文献[13－14]先建立墙背填土内摩擦角和挡土墙位移之间的关系式，并在文献[13]的基础上，建立一种改进的考虑位移影响的无黏性土主动土压力计算方法。

2 位移和摩擦角的关系

主动土压力是指当挡土墙向离开土体方向偏移至土体达到极限平衡状态时，作用在墙上的土压力。Bang[13]指出，从初始主动状态到极限主动状态是一个渐进变化的过程，二者之间存在一个中间主动状态。对于绕墙底向外转动的挡土墙，在土压力作用下，当挡土墙顶达到某位移 sc时，墙顶背面土体内摩擦角达到φ，墙底背面土体内摩擦角为0，墙底和墙顶之间背面土体内摩擦角由0到φ 线性分布，此时定义为初始主动状态；随着挡土墙绕墙底向外转动，墙底背面土体内摩擦角由0逐渐增加到φ，墙顶背面土体内摩擦角不变，墙底和墙顶之间背面土体内摩擦角同样服从线性分布，墙底背面土体内摩擦角达到φ 之前，定义为中间主动状态，墙底背面土体内摩擦角达到φ 之后，此时定义为极限主动状态。位移 sc定义为临界位移，沿墙背取值不变，即墙背任意位置水平位移只要达到 sc，该位置土体即达到极限平衡状态。sc大小与墙背填土内摩擦角、密实度无关，与挡土墙位移模式无关，取值范围为0.0003H～0.0005H，H为挡土墙墙高[14]。Bang定义的内摩擦角分布没有反映挡土墙位移大小的影响。

Chang[14]认为，墙背土体内摩擦角发挥值φm、墙-土摩擦角发挥值δm分别随位移线性地从初始值0φ、δ0增加到极限值φ、δ 。当墙后某点位移s ≥sc时，φm、δm完全发挥，分别取极限值φ、δ ；当墙后某点位移s＜ sc时，φm、δm定义为发挥值，由位移通过线性插值计算。Chang提出的摩擦角分布关系[14]表明，无论挡土墙位移多大，墙底处土体摩擦角始终取初始摩擦角，由推导的土压力分布也可以看出，墙底处土压力分布值并不是随着挡土墙位移的增加由静止土压力值渐进地减小到主动土压力值。

基于Bang[13]和Chang[14]对内摩擦角和挡土墙位移之间关系的研究，根据挡土墙墙顶位移sa和临界值sc之间的关系，建立墙后土体内摩擦角沿墙背分布关系式。分两种情况：墙顶位移sa不大于临界值 sc；墙顶位移 sa大于临界值sc，如图1所示。

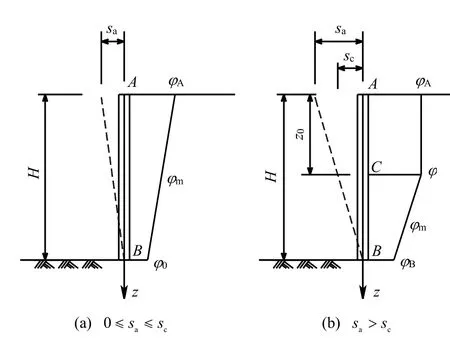
图1 内摩擦角与位移关系示意图Fig.1 Schematic diagrams of internal friction angle and displacement

（1）0≤ sa≤sc

如图1(a)所示，墙顶背面土体内摩擦角为

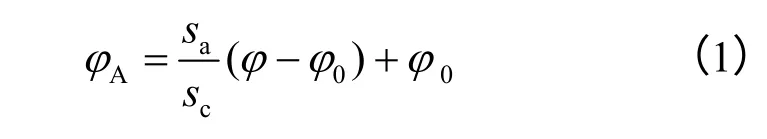
式（1）表明φA随位移 sa的增大由φ0线性增加到φ。

墙底背面土体内摩擦角为

墙背任意深度z 处土体内摩擦角φm由墙顶和墙底背面土体内摩擦角通过线性插值求得

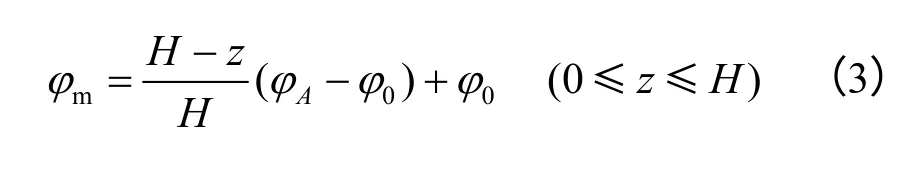
（2）sa＞sc

如图1(b)所示，令挡土墙位移s ≥ sc的挡土墙深度范围为 z0，即图1(b)中AC 段，则有

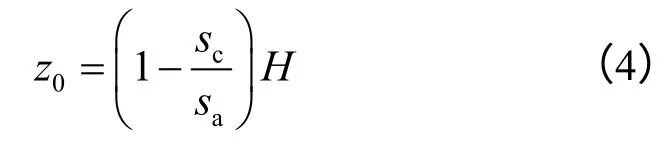
该范围内土体都达到极限平衡状态，墙背土体内摩擦角为

墙底背面土体内摩擦角为

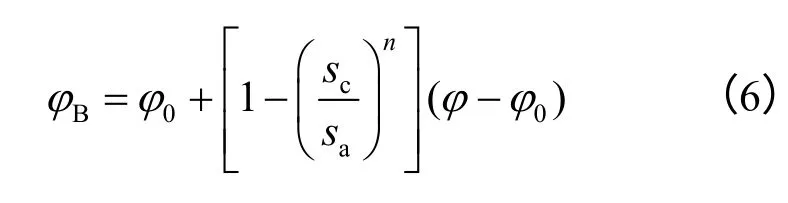
式中：n ＞0，n∈R，反映墙底背面土体内摩擦角随sa变化的快慢。n=1时，1-sc/sa相当于文献[13]中参数β 。式（6）表明，当 sa由sc增加到∞时，φB按式（6）由φ0增加到φ。

图1(b)中CB 段挡土墙位移s ＜sc，该段φm服从线性分布，由B 点的φB和C 点的φ 通过线性插值求得

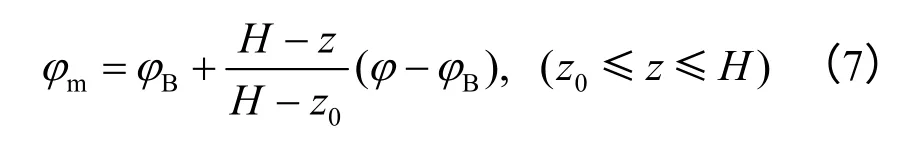
由式（3）、（5）、（7）即可计算墙顶任意位移时，墙背任意点土体内摩擦角。上述关系式既考虑位移大小对墙背土体内摩擦角的影响，也体现了墙底背面土体内摩擦角渐进发展的特点。

3 主动土压力计算

3.1 Bang主动土压力计算公式

Bang[13]假定平衡状态时墙后土体内形成系列滑裂面，滑裂面与水平方向的倾角等于45°+φm2，大小取决于滑裂面与挡土墙交点位置的水平位移。根据库仑土压力理论，由滑裂面上土楔体的静力平衡条件，求得作用在挡土墙上的土压力合力，由该合力关于滑裂面和挡土墙交点位置坐标z 的导数，求得该处土压力分布解。Bang提出的主动土压力计算公式[10]为

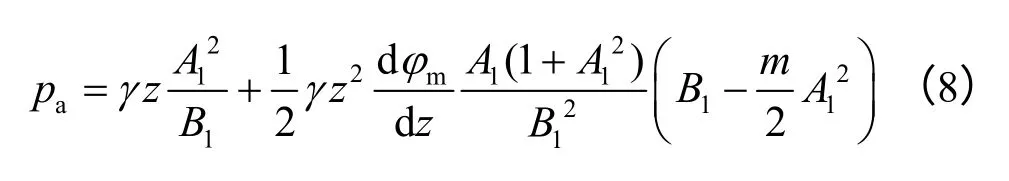
式中：γ为墙背土体重度；m、A1、B1为参数，且有

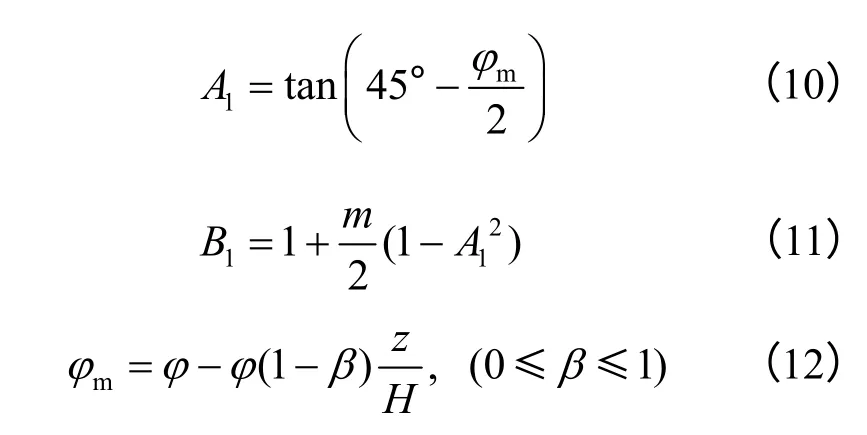
式（12）中，β为参数，β=0，对应Bang定义的初始主动状态；类似的，β=1，对应极限主动状态；0＜β ＜1，对应中间主动状态。文献[14]指出只有挡土墙位移达到临界值 sc，该处土体才达到极限平衡状态，相应的内摩擦角取φ。由此可知，Bang提出的土压力公式只适用于墙顶位移 sa＞sc时的主动状态土压力计算，且Bang计算公式中没有反映挡土墙位移大小的影响，通过指定参数β 来计算不同状态时墙背土压力分布。

3.2 改进的主动土压力计算公式

为反映位移大小对土压力的影响，利用式（8）和式（3）、（5）、（7），建立一种改进的考虑位移影响的主动土压力计算公式。Bang计算公式假定墙-土摩擦角δ为常数，本文沿用这个假定。

3.2.1 sa≤scm

φ 由式（3）计算，则有

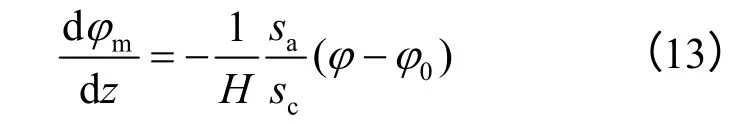
墙背土压力分布为

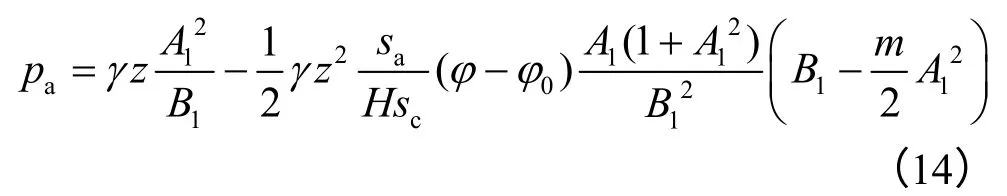
m、A1、B1由式（9）～（11）计算。由式（14）可计算Bang定义的初始主动状态之前的墙背土压力。

3.2.2 sa＞sc

（1）AC 段土压力分布

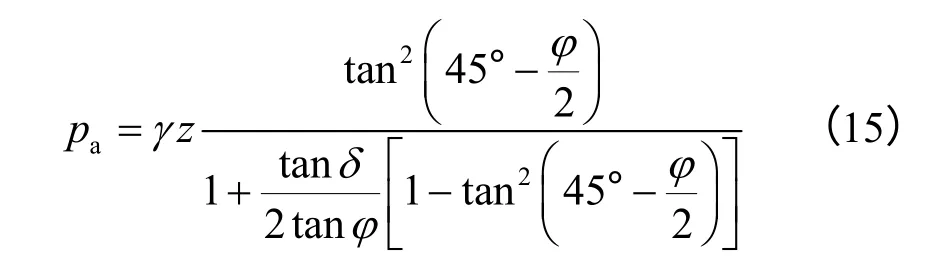
（2）CB 段土压力分布

φm由式（7）计算，则有

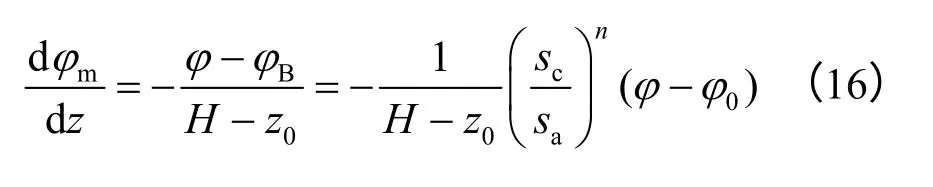
AC 段墙背土体处于极限平衡状态，CB 段墙背土体处于非极限平衡状态。计算CB 段墙背土压力时，将AC 段墙背土体假定为超载，并认为其只影响式（8）右边第1项，由此得CB 段土压力计算公式为

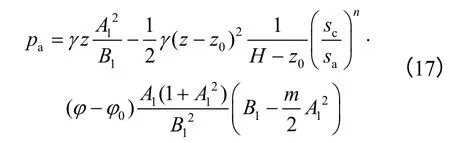
3.3 改进方法的计算结果

图2为由本文方法计算的挡土墙墙顶不同位移大小时的墙背土压力分布。计算所采用的墙土参数为[13]：H=3 m，γ=15.7 kN/m3，φ=30°，墙背光滑，φ0=0。

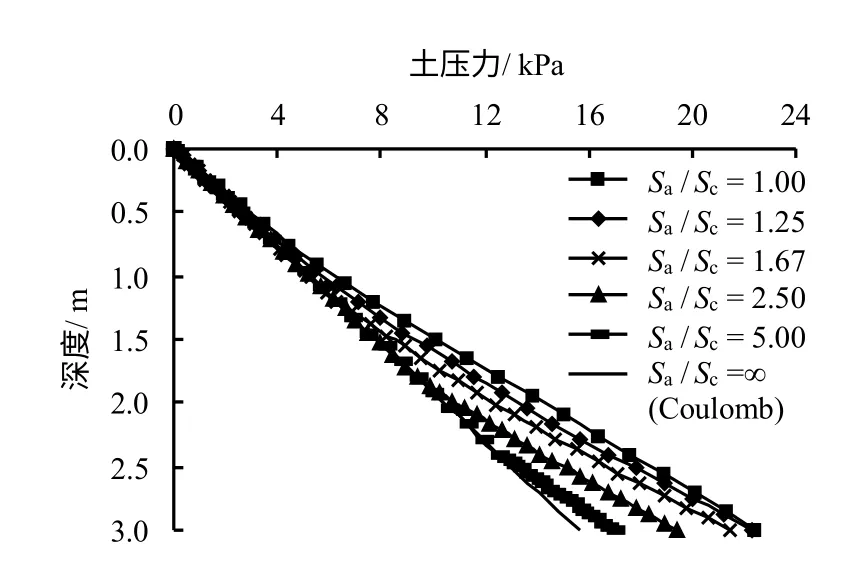
图2 不同位移时墙后主动土压力分布Fig.2 Distribution of active earth pressure behind retaining wall with different displacements

由本文计算方法推导过程和图中曲线关系可知，sa/sc=1时，仅墙顶背面土体达到极限平衡状态；随着 sa/sc的增加，达到极限平衡状态的范围逐渐向下扩展，挡土墙位移s ≥ sc范围的墙背土体均达到极限平衡状态，相应的土压力等于库仑主动土压力。而Bang计算方法表明，s ≥ sc范围的墙背土体处于非极限平衡状态，墙后土压力大于库仑土压力，只有当s 充分大时，即Bang方法中β=1，墙背土体才达到极限平衡状态，相应的墙背土压力等于库仑主动土压力。可见，与Bang方法相比，本文方法考虑了位移大小的影响。sa/sc=1时的土压力分布相当于Bang方法中β=0时的土压力分布，而 sa/sc=∞时的土压力分布相当于Bang方法中β=1时的土压力分布。在这二者之间，若令β=1-sc/sa，Bang方法计算的土压力大于本文方法计算的土压力。与Chang计算方法相比，Chang方法考虑了位移大小的影响，但由Chang方法计算的墙底处土压力，只有在 sa/sc趋于无穷大时，才等于库仑主动土压力，在这之前，均等于静止土压力；而本文方法计算的墙底处土压力是随着墙顶位移的增加，由静止土压力值逐渐地减小到库仑主动土压力值。

表1为不同位移大小时相应的土压力合力和作用点位置。表中 h0/ H为土压力合力作用点距离墙底距离h0和墙高H 之比。墙顶位移sa达到临界值 sc后，墙背上部土体先达到极限平衡状态，土压力由静止土压力减小到库仑主动土压力，合力作用点位置下降；随着挡土墙位移的增加，挡土墙下部土体逐渐达到极限平衡状态，土压力相应地收敛于库仑主动土压力，合力作用点位置也相应上移，这与Fang的试验结论是一致的。土压力合力随挡土墙位移的增加而逐渐减小，最后趋近于库仑主动土压力。

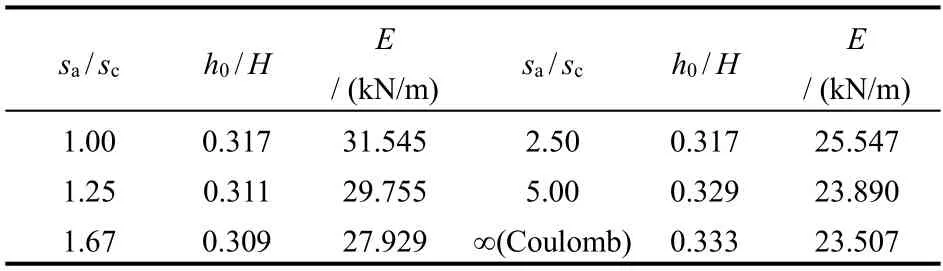
表1 不同位移时土压力合力及作用点位置Table 1 Resultant force and application point of earth pressure with different displacements

4 与模型试验结果对比

Fang等[4]对挡土墙绕墙底向外转动时墙后主动土压力分布进行了室内模型试验研究，填土为砂土。模型试验参数为：H=1.016 m，墙背直立，γ=15.34 kN/m3，φ=33.4°，φ0=7.5°，δ=16.7°。

图3给出了室内模型试验结果，同时给出了由本文理论公式计算的结果。

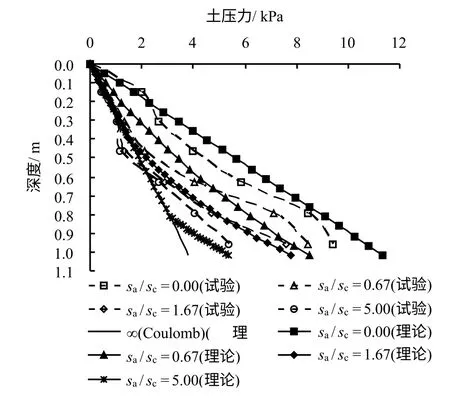
图3 计算土压力和模型试验结果对比Fig.3 Comparison of computational earth pressure and model test results

图3中数据对比表明：本文方法计算结果与模型试验结果吻合较好。理论计算和试验结果都表明，当挡土墙位移达到临界值sc后，墙后土压力均趋近库仑主动土压力，随着挡土墙位移的增加，墙底处土压力也逐渐地收敛到库仑主动土压力。同样，文献[14]也与该模型试验结果进行了对比，但文献[14]中土压力计算方法不能反映墙底处土压力渐进收敛过程。

表2为理论公式计算和模型试验实测得出的土压力合力和作用点位置结果。由表中数据可知，随着挡土墙位移的增加，土压力合力逐渐减小；作用点位置先下降，后上移；当挡土墙位移充分大时，理论计算的墙后土压力合力等于库仑主动土压力，作用点位置位于挡土墙下1/3点。

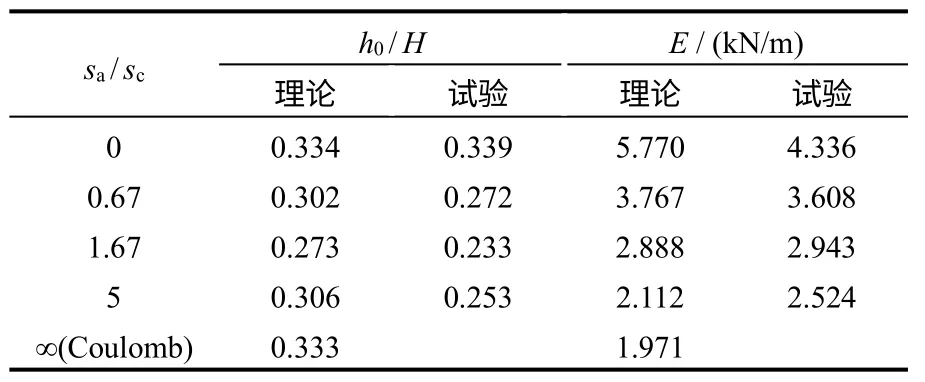
表2 理论计算和模型试验土压力合力及作用点位置Table 2 Resultant forces and application points of earth pressure for theoretical computation and model tests

5 结论

（1）基于土压力形成机制的分析及已有的研究成果，建立了挡土墙位移和墙背土体内摩擦角发挥值之间的关系式，提出了一种改进的考虑位移影响的主动土压力计算方法。

（2）本文提出的计算方法能反映墙背土压力及墙背土体抗剪强度随挡土墙位移的增加而逐渐形成的过程；由本文方法计算的墙底处土压力也是随着挡土墙位移的增长而逐步收敛于库仑主动土压力。

（3）与模型试验结果对比表明，本文理论公式计算结果与模型试验结果吻合较好。

[1]TERZAGHI K.Theoretical soil mechanics[M].New York:John Wiley and Son，1943.

[2]TERZAGHI K.Record earth pressure testing machine[J].Engineering News Record，1932，109(29):365－369.

[3]SHERIF M A，FANG Y S. Kaand K0behind rotating and non-yielding walls[J].Journal of Geotechnical Engineering，1984，110(1):41－56.

[4]FANG Y S，ISHIBASHI I.Static earth pressure with various wall movements[J].Journal of Geotechnical Engineering，ASCE，1986，112(3):317－333.

[5]周应英，任美龙.刚性挡土墙主动土压力的试验研究[J].岩土工程学报，1990，12(2):19－26.ZHOU Ying-ying，REN Mei-long.An experiment study on active earth pressure behind rigid retaining wall[J].Chinese Journal of Geotechnical Engineering，1990，12(2):19－26.

[6]徐日庆，廖斌，吴渐，等.黏性土的非极限主动土压力计算方法研究[J].岩土力学，2013，34(1):148－155.XU Ri-qing，LIAO Bin，WU Jian，et al.Computational method for active earth pressure of cohesive soil under nonlimit state[J].Rock and Soil Mechanics，2013，34(1):148－155.

[7]徐日庆，龚慈，魏纲，等.考虑平动位移效应的刚性挡土墙土压力理论[J].浙江大学学报(工学版)，2005，39(1):119－122.XU Ri-qing，GONG Ci，WEI Gang，et al.Theory of earth pressure against rigid retaining walls considering translational movement effect[J].Journal of Zhejiang University (Engineering Science)，2005，39(1):119－122.

[8]杨泰华，贺怀建.考虑位移效应的土压力计算理论[J].岩土力学，2010，31(11):3635－3639.YANG Tai-hua，HE Huai-jian.Earth pressure calculation theory considering displacement effects[J].Rock and Soil Mechanics，2010，31(11):3635－3639.

[9]卢坤林，杨扬.非极限主动土压力计算方法初探[J].岩土力学，2010，31(2):615－619.LU Kun-lin，YANG Yang.Preliminary study of earth pressure under non-limit state[J].Rock and Soil Mechanics，2010，31(2):615－619.

[10]施建勇，雷国辉，艾英钵，等.土压力变化规律的应力路径三轴试验研究[J].岩土力学，2005，26(11):1700－1704.SHI Jian-yong，LEI Guo-hui，AI Ying-bo，et al.Stress path controlled triaxial experimental study of lateral earth pressure behaviour[J].Rock and Soil Mechanics，2005，26(11):1700－1704.

[11]CLOUGH G W，DUNCAN J M.Finite element analysis of retaining wall behavior[J].Journal of the Soil Mechanics and Foundation，ASCE，1971，97(SM12):1657－1673.

[12]陈页开，汪益敏，徐日庆，等.刚性挡土墙主动土压力数值分析[J].岩石力学与工程学报，2004，23(6):989－995.CHEN Ye-kai，WANG Yi-min，XU Ri-qing，et al.Numerical analysis of active earth pressure on rigid retaining wall[J].Chinese Journal of Rock Mechanics and Engineering，2004，23(6):989－995.

[13]BANG S.Active earth pressure behind retaining walls[J].Journal of Geotechnical Engineering，1985，111(3):407－412.

[14]CHANG M F.Lateral earth pressure behind rotating walls[J].Canadian Geotechnical Journal，1997，34(2):498－509.