两个非线性偏微分方程强解的持续性质

贺婷婷， 马飞遥

(宁波大学 数学系 非线性科学研究中心 浙江 宁波 315211)



两个非线性偏微分方程强解的持续性质

贺婷婷， 马飞遥

(宁波大学 数学系 非线性科学研究中心 浙江 宁波 315211)

给出了两个非线性偏微分方程，即耦合的Camassa-Holm-Novikov方程和两分量的Novikov方程强解的持续性质.通过构造权重函数，并利用Gronwall不等式，得到相关估计，从而证明了这两个偏微分方程的持续性质.

Camassa-Holm-Novikov方程； 两分量的Novikov方程； 持续性质

0 引言

近年来，著名的耦合的Camassa-Holm-Novikov方程越来越得到数学和物理工作者们的关注[1],该方程为

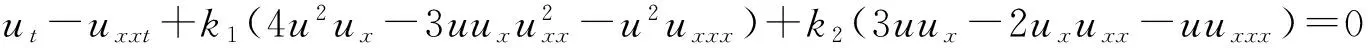
(1)

特别的，当k1=0,k2=1时，方程(1)就变成著名的非周期的Camassa-Holm方程，即

ut-uxxt+3uux-2uxuxx-uuxxx=0.

它是Fuchssteiner等[2]在1981年研究遗传对称性时发现的，是流体力学中的一个非常重要的非线性偏微分方程.1993年，Camassa等[3]在浅水波理论中导出了该方程，因此，它被称为Camassa-Holm方程(CH方程).CH方程有无穷多守恒积分、双哈密顿结构和尖峰孤立子解.后来研究者们进一步研究了CH方程的局部适定性[4-5]、爆破现象[6-7]和全局解的存在性[8].文[9-11]研究了CH方程的持续性质，并得到了它的孤子解.

此外，当k1=1,k2=0时，方程(1)又变成Novikov方程，即

该方程是Novikov[12]在研究非局域的带有平方项或立方项的非线性偏微分方程的对称分类时发现的，他还找到了Novikov方程的Lax对，证明了它的可积性.Hone等[13]发现了该方程的无穷多守恒量、矩阵形式的Lax对和双哈密顿结构，还计算出它的多孤子解.Ni等[14]证明了它的局部适定性.

(2)

本文研究的第2个方程，即著名的两分量Novikov方程，

(3)

该方程是Geng等[15]于2009年提出来的.随后，他们又计算出该方程的N孤子解和守恒量.Mi等[16]证明了该方程的局部适定性.Li等[17]得到了两分量Novikov方程的双哈密顿系统.

为了便于展开证明，将方程(3)写成它的等价形式，

(4)

对于偏微分方程强解的持续性的研究是十分必要的[18].关于Novikov方程[14]、DGH方程[15]、两分量的CH方程[19]、两分量的DP方程[20]和两分量的DGH方程[21]等的持续性质的研究结果相继问世.在此基础上，作者研究了耦合的Camassa-Holm-Novikov方程和两分量的Novikov方程的持续性质.

1 主要结果

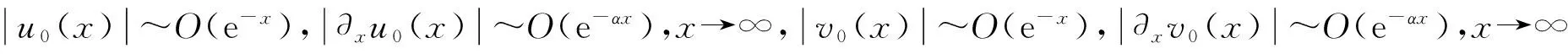
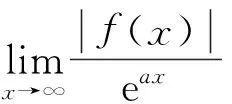
目前还没能证明方程(2)和(4)的唯一连续性质和无穷传播速度.

2 定理的证明

定理1的证明为了方便起见，首先引入符号，

(5)

证明思路是通过估计‖u(x,t)‖∞和‖ux(x,t)‖∞得到想要的结果.

第1步首先估计‖u(x,t)‖∞.

方程(2)两边同乘以u2n-1(n∈Z),再对方程两边关于x积分，得

∫Rutu2n-1dx+k1∫Ru2uxu2n-1dx+k2∫Ruuxu2n-1dx+

k1∫Ru2n-1G*E(u)dx+k2∫Ru2n-1∂xG*F(u)dx=0.

(6)

考虑式(6)中的左边第1项，有

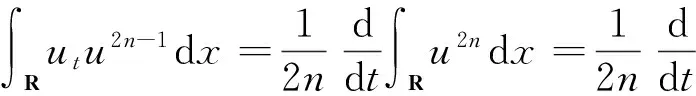
对左边第2项有

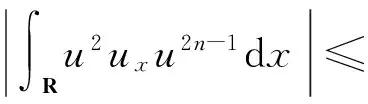
对左边第3项有

应用Hölder不等式，得到左边最后2项的估计结果分别为

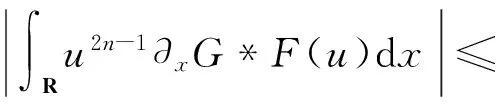
把上面所有的估计结果代入式(6)，整理可得

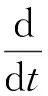
A(‖u(t)‖∞‖ux(t)‖∞+‖ux(t)‖∞)‖u(t)‖2n+

A‖G*E(u)‖2n+A‖∂xG*F(u)‖2n,

在上式中应用Gronwall’s不等式，得

对于任意的函数f∈L1(R)∩L∞(R),应有

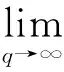
(7)

因此，令n→∞，可得

第2步估计‖ux(x,t)‖∞.

对方程(2)两边同时关于x求导，可得

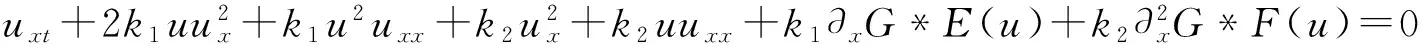
为了去掉二阶导数项，利用分部积分对上式中的第3项和第5项处理，可得

类似地，可以得到下面的不等式:

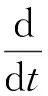
A(‖u(t)‖∞‖ux(t)‖∞+‖ux(t)‖∞)‖ux(t)‖2n+

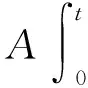
利用Gronwall’s不等式得

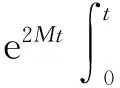
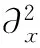
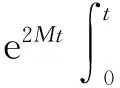
于是，得到关于‖u(t)‖∞和‖ux(t)‖∞的估计,

‖u(t)‖∞+‖ux(t)‖∞≤e2Mt(‖u(0)‖∞+‖ux(0)‖∞)+

利用式(5)中的符号E(u),F(u),从方程(2)中可得

∂t(uφN)+k1u2φNux+k2uφNux+k1φNG*E(u)+k2φN∂xG*F(u)=0.

因此，同理可得

和文[18]中一样，利用一些小技巧对上式中出现二阶导数的项处理，可得

因此，与无权重函数时的情形一样，重复前面的步骤，可得

‖u(t)φN‖∞+‖ux(t)φN‖∞≤e2Mt(‖u(0)φN‖∞+‖ux(0)φN‖∞)+

(8)

第3步通过简单的计算可知，存在一个仅依赖于θ∈(0,1)的常数C>0,使得对任意给定的N∈Z+,有

(9)

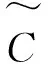
于是有

(10)

(11)

(12)

(13)

(14)

(15)

(16)

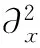
(17)

因此，将式(10)～(17)代入式(8)中，并利用式(5)和Gronwall’s不等式的积分形式，得

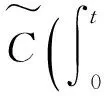
因此，对于任意的n∈Z+和t∈[0,T],都有

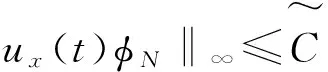
最后，在上式中令N→∞,有

定理2的证明在证明定理2的过程中将会用到定理1的结论.

对任意的t1∈[0,T],对方程(2)两边同时关于时间t在区间[0,t1]上积分,可得

(18)

利用定理1可得,

下面证明式(18)中左边的后两项是O(e-x)，于是有

从已知条件和定理1可知，h(x)～O(e-x),x→∞,因此,

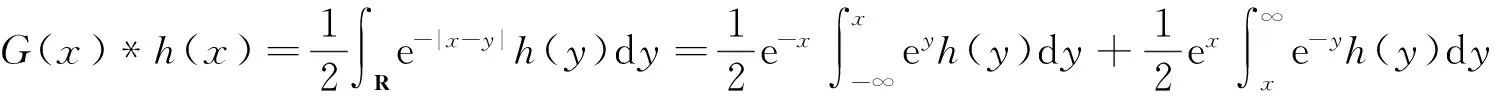
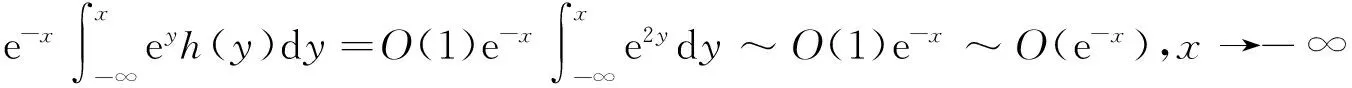
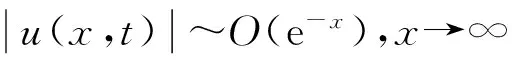
定理3的证明为方便起见，首先引入符号

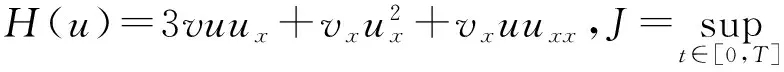
第1步估计‖u(x,t)φN‖∞.

方程(4)两边同时乘以φN(uφN)2n-1(n∈Z),然后方程两边同时关于x微分,得

∫RutφN(uφN)2n-1dx+∫RvuuxφN(uφN)2n-1dx+∫RφN(uφN)2n-1∂xG*(vxuux)dx+

∫RφN(uφN)2n-1G*H(u)dx=0.

仿照定理1的证明，对上式中每一项做估计，整理,得到

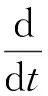
‖φN∂xG*(vxuux)‖2n+‖φNG*E(u)‖2n.

运用Gronwall’s不等式,可得

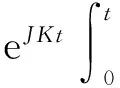
在上式中，令n→∞,再结合式(7)得

(19)

第2步估计‖ux(x,t)φN‖∞.

对方程(4)两边同时关于x微分，可得

上式两边同时乘以φN(uxφN)2n-1(n∈Z),得

∫R(uxφN)2n-1φN∂xG*H(u)dx=0.

为了消去上式中左边第4项的二阶导数项，对第4项做分部积分，于是有

同理可得

‖v(t)‖∞+‖u(t)‖∞‖ux(t)φN‖2n+

运用Gronwall’s不等式得，

上式中令n→∞,再结合式(7)可得

因此,结合式(19)和上式，得到‖u(t)φN‖∞和‖ux(t)φN‖∞的估计结果，即

‖u(t)φN‖∞+‖ux(t)φN‖∞≤e2JKt(‖u(0)φN‖∞+‖ux(0)φN‖∞)+

(20)

第3步利用式(9)可以得到如下的估计，

(21)

同理可得

(22)

于是，将式(21)～(22)代入到式(20)，并利用式(5)和Gronwall’s不等式的积分形式,可得

‖u(t)φN‖∞+‖ux(t)φN‖∞≤

‖ux(τ)‖∞‖vx(τ)‖∞)(‖φNu‖∞+‖φNux‖∞)dτ≤

因此，对任意的n∈Z+和t∈[0,T],有

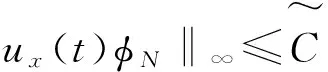
最后，在上式中令N→∞,从而发现对任意的t∈[0,T],

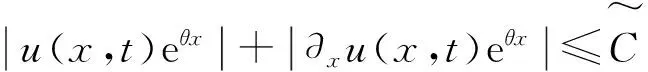
考虑到方程(4)中第1和2式的对称性，只需证明方程(4)中第1式的持续性质，方程(4)中第2式的持续性质自然可得，即

定理4的证明在证明定理4的过程中将用到定理3的结论.

对任意给定的时间t1∈[0,T],对方程(4)中第1式两边同时关于t在区间[0,t1]上积分，得

(23)

由定理3的结论可得

下面将证明式(23)中的最后两项是O(e-x),有

由已知条件和定理3可知，当x→∞时，vxuux～O(e-x),又因为

于是有

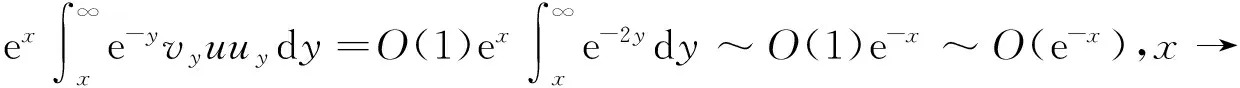
因此，

类似地，由H(u)～O(e-x)可得

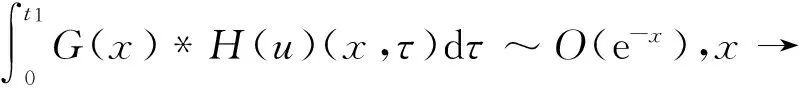
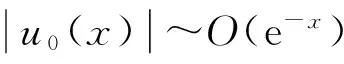
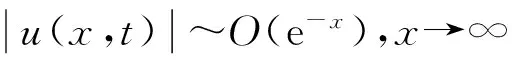
类似地，由方程(4)中第1和2式的对称性，自然可得关于v(x,t)的类似结论,即

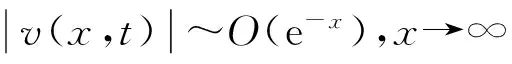
在区间[0,T]上一致成立.

参考文献：

[1] 李壹宏.一类耦合方程的单孤子解[J].纯粹数学与应用数学，2013，29(3)：287-292.

[2] Fuchssteiner B, Fokas A. Sympletic structures,their backlund transformations and hereditary symmetries[J]. Phys D, 1981,4(1):47-66.

[3] Camassa R, Holm D D. An integrable shallow water wave equation with peaked solutions[J]. Phys Rev Lett, 1993,71(11):1661-1664.

[4] Himonas A A, Misiolek G. The Cauchy problem for an integrable shallow-water equation[J]. Differential and Integral Equations, 2001,14(7):821-831.

[5] Rodríguez-Blanco G. On the Cauchy problem for the Camassa-Holm equation[J]. Nonlinear Anal,2001,46(3):309-327.

[6] Jiang Zaihong, Ni Lidao, Zhou Yong. Wave breaking of the Camassa-Holm equation[J]. Journal of Nonlinear Science, 2012,22(2):235-245.

[7] McKean H P. Breakdown of a shallow water equation[J]. The Asian Journal of Mathematics, 1998,2(4):867-868.

[8] Xin Zhongping, Zhang Ping. On the weak solutions to a shallow water equation[J]. Communications on Pure and Applied Mathematics, 2000,53(11):1411-1433.

[9] Himonas A A, Misiolek G, Ponce G, et al. Persistence properties and unique continuation of solutions of the Camassa-Holm equation[J]. Communications in Mathematical Physics, 2007,271(2):511-522.

[10]Constantin A, Strauss W A. Stability of peakons[J]. Communications on Pure and Applied Mathematics, 2000,53(5):603-610.

[11]Ni Lidao, Zhou Yong. A new asymptotic behavior of solutions to the Camassa-Holm equation[J]. Proc Amer Math Soc, 2012,140(2):607-614.

[12]Novikov V. Generalizations of the Camassa-Holm equation[J]. J Phys A, 2009,42(34):2002-2016.

[13]Hone A N W, Lundmark H, Szmigielski J. Explicit multipeakon solutions of Novikov’s cubically nonlinear integrable Camassa-Holm type equation[J]. Dyn Partial Differ Equ, 2009,6(3):253-289.

[14]Ni Lidao, Zhou Yong. Well-posedness and persistence properties for the Novikov equation[J]. J Differential Equations, 2011,250(7):3002-3021.

[15]Geng Xianguo, Xue Bo. An extension of integrable peakon equations with cubic nonlinearity[J]. Nonlinearity, 2009,22(8):1847-1856.

[16]Mi Yongsheng, Mu Chunlai, Tao Weian. On the Cauchy problem for the two-component Novikov equation[J]. Mathematical Physics, 2013, 2013:810725.

[17]Li Nianhua, Liu Qingping. On bi-Hamiltonian structure of two-component Novikov equation[J]. Phys Lett A, 2013,377(3/4):257-261.

[18]Zhou Yong, Guo Zhengguang. Blow up and propagation speed of solutions to the DGH equation[J]. Discrete Contin Dyn Syst Ser B, 2009,12(3):657-670.

[19]Guo Zhengguang, Ni Lidao. Persistence properties and unique continuation of solutions to a two-component Camassa-Holm equation[J]. Math Phys Anal Geom, 2011,14(2):101-114.

[20]Fu Ying, Qu Changzheng. Unique continuation and persistence properties of solutions to the two-component Degaperis-Procesi equations[J]. Acta Mathematica Scientia, 2012,32B(2):652-662.

[21]Zhai Panpan, Guo Zhengguang, Wang Weiming. Blow up phenomena and persistence properties of solutions to the two-component DGH equations[J]. Abstract and Applied Analysis, 2013, 2013:750315.

Persistence Properties for Two Kinds of Nonlinear Partial Differential Equations

HE Ting-ting, MA Fei-yao

(CenterofNonlinearStudies,FacultyofMathematics,NingboUniversity,Ningbo315211,China)

The persistence properties of two kinds of partial differential equations, i.e.a coupled Camassa-Holm-Novikov equation and a two component Novikov equation were investigated. On the basis of constructing weight function, and combing with the Gronwall’s inequality, the related estimates were obtained.

Camassa-Holm-Novikov equation; two component Novikov equation; persistence property

2014-08-06

宁波自然科学基金资助项目，编号2012A610033.

贺婷婷(1990-),女，甘肃庆阳人，硕士研究生，主要从事数学物理研究，E-mail: hetingting_3901@163.com;通讯作者：马飞遥(1979-)，男，湖南衡阳人，讲师，主要从事偏微分方程研究，E-mail: mafeiyao@nbu.edu.cn.

O175.2

A

1671-6841(2015)01-0014-10

10.3969/j.issn.1671-6841.2015.01.004