均布荷载下一次超静定梁的弹塑性全过程分析
2015-02-11罗运阔李会知
罗运阔, 李会知
(1.郑州大学 土木工程学院 河南 郑州 450001;2.开封市通达公路工程有限公司 河南 开封 475003)
均布荷载下一次超静定梁的弹塑性全过程分析
罗运阔1,2, 李会知1
(1.郑州大学 土木工程学院 河南 郑州 450001;2.开封市通达公路工程有限公司 河南 开封 475003)
对均布荷载加载作用下一次超静定梁的弹塑性变形全过程进行了分析.根据受力变形的特点,均布荷载下一次超静定梁的加载过程可分成4个阶段,分别是弹性阶段,固支端附近塑性变形区扩展阶段,固支端保持为塑性铰而固支端附近塑性变形区卸载阶段,固支端保持为塑性铰而梁中部出现塑性变形区并扩展直至中部某点形成塑性铰阶段.在弹性的第1阶段,弯矩内力、挠度与外荷载是线性比例关系;在第2阶段,弯矩内力、挠度与外荷载是复杂的非线性关系;在第3阶段,弯矩、挠度与外荷载是线性关系但不是比例关系;在第4阶段,弯矩与外荷载的关系与第3阶段相同,但挠度与外荷载是更复杂的非线性关系.给出了弹塑性全过程各阶段任意点的弯矩和挠度计算公式,可供结构设计应用.
超静定梁; 弹塑性; 塑性铰; 均布荷载; 挠度
0 引言
梁的受力变形数据是结构强度和刚度分析的基础.在线弹性范围内,梁的受力变形分析已是成熟的理论[1].在塑性条件下,应力-应变本构关系是非线性的,使得超静定梁的受力变形解析分析成为复杂的难题,现有研究主要依赖于数值方法来解决[2-3].曹天捷[4]、李会知[5-7]和樊友景[8]解析讨论了几种工况的超静定梁的受力和变形.但李会知的前期研究中忽视了塑性铰的转动对悬臂梁基本体系的否定,造成出现塑性铰后的位移公式存在错误.本文对跨中均布荷载作用下单跨一次超静定梁的弹塑性加载和变形全过程进行了分析,在出现塑性铰后,采用简支梁体系来分析,是一次完善性质的解析研究,给出了全过程各阶段任意点的弯矩和挠度计算公式,可供结构设计者参考和应用.
1 弹性阶段
单跨一次超静定梁和所受均布荷载如图1.已知梁是矩形截面梁,b,h分别是梁宽和梁高,梁材料是理想弹塑性材料,材料屈服应力是σs.梁的弯矩内力和挠度随均布荷载q的变化是分析梁强度和刚度的数据基础.
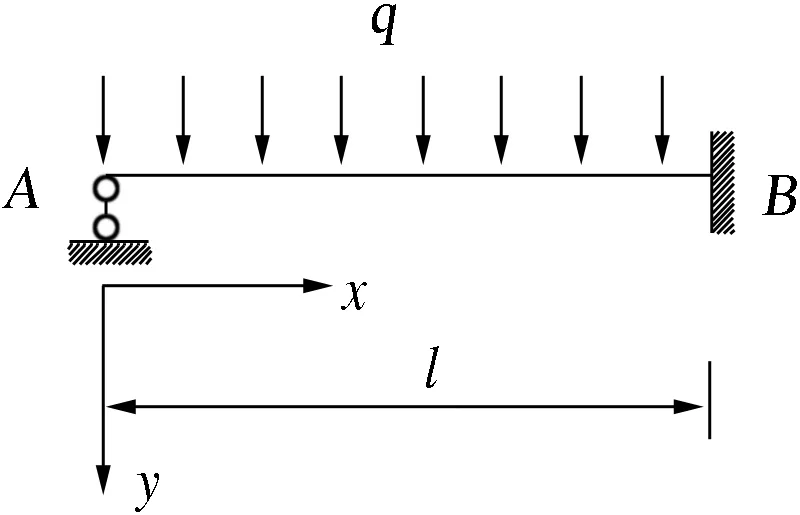
图1 一次超静定梁
利用材料力学理论[1]不难得出弹性阶段的结果,约束力、弯矩内力和挠度曲线分别是

(1)
上述各式表明弹性阶段的约束力、弯矩内力和挠度均随外荷载q的增加按线性比例增加.当固支端弯矩达截面弹性极限弯矩Me=bh2σs/6时,外荷载q达弹性极限qe=8Me/l2.
2 固支端附近塑性变形区扩展阶段

分析挠度w采用公式
(2)
下面以公式(2)为基本理论依据,分析图1梁出现塑性变形后弯矩和挠度随外荷载q的变化.
图1超静定梁的弯矩分布通过点A的约束力FA表达为

(3)
只要确定了FA与荷载q的关系,就确定了梁的弯矩内力随荷载的变化情况.
取图2所示的悬臂梁作为基本体系来分析讨论FA和q的关系.当荷载q和FA作用下基本体系A点的挠度wA=0时,FA就是图1梁的约束力.本加载阶段公式(3)的弯矩如图3,图3的x=a处弯矩为弹性极限弯矩Me,固支端附近弹塑性段(a (4) 图4是基本体系只在点A加竖向单位荷载的弯矩图,根据公式(2)求出点A的挠度wA并令wA=0,得FA和q关系如下 (5) 由式(5)可见约束力FA与荷载q是非线性关系,进一步可知,由公式(3)表达的弯矩内力M与荷载q也是复杂的非线性关系. 先确定本加载阶段的荷载范围.令式(3)中的点B弯矩FAl-ql2/2=-Mu=-1.5Me,联立式(5)得q=13.121 6Me/l2,FA=5.060 8Me/l,再代入公式(3)得0 (6) (7) 当a≤x≤l时,挠度方程为 (8) 挠度公式(7),(8)中的FA由式(5)确定,a由式(4)确定.可以看出,出现塑性变形后,挠度与外荷载q是非线性关系. 图2 基本体系 图3 弹塑性弯矩图(qe 图4 点A单位荷载弯矩图 图5 点X单位荷载弯矩图 当荷载q≥q1时,固支端成为塑性铰,塑性铰受约束转动,原超静定梁结构变成静定结构,等效于简支梁,力学等效结构如图6.只是随着外荷载q的增加,变成简支的右端恒作用着弯矩Mu=1.5Me,约束力和梁的弯矩分布为 (9) 可见弯矩M与q虽是线性关系,但不是比例关系,给定外荷载q时,即可由式(9)求出梁任意位置的弯矩内力. 虽然受力分析简单,但挠度计算仍很复杂.由于塑性铰引起的内力分布发生改变,使得随着荷载q增加,上一阶段结束时的弹塑性变形区域(a1≤x≤l)发生线性卸载,当a1≤x≤l时,曲率为 (10) (11) 当a1≤x≤l时,挠度方程为 (12) 挠度公式(11),(12)表明,在本加载阶段,挠度与外荷载q是线性关系但不是比例关系. 在本加载阶段(q2≤q≤qu),固支端仍保持为塑性铰,结构还是等效于静定的简支梁结构.图9是本阶段的弯矩分布图,弯矩分布与外荷载q关系仍由式(9)表达.随着荷载增加,梁中间部分出现弹塑性段,设其范围为c≤x≤b,令式(9)弯矩为Me,得 (13) 本加载阶段的变形特点是塑性区扩展与卸载并存.在c 与上同理可求挠度曲线,只是过程和结果更复杂.当0≤x≤c时,挠度方程为 (14) 当c≤x≤b时,挠度方程为 (15) 当b≤x≤a1时,挠度方程为 (16) 当a1≤x≤l时,挠度方程为 (17) 挠度式(14)~(17)表明,在本加载阶段,挠度与外荷载q是更为复杂的非线性关系. 图6 等效结构 图7 弹塑性弯矩图 图8 点X单位荷载弯矩图 图9 弹塑性弯矩图(q2 分析了均布荷载作用下一次超静定理想弹塑性矩形截面梁的受力变形全过程.根据受力变形的特点,均布荷载作用下一次超静定梁的加载过程可分为4个阶段,分别是弹性阶段,固支端附近塑性变形区扩展阶段,固支端保持为塑性铰而固支端附近塑性变形区卸载阶段,固支端保持为塑性铰而梁中部出现塑性变形区并扩展直至中部某点形成塑性铰阶段.在弹性的第1阶段,弯矩内力、挠度与外荷载是线性比例关系.出现塑性变形后,弯矩内力、挠度与外荷载不再是简单的比例关系.在第2阶段,弯矩内力、挠度与外荷载是复杂的非线性关系.在第3阶段,弯矩、挠度与外荷载是线性关系但不是比例关系.在第4阶段,弯矩与外荷载的关系与第3阶段相同,但挠度与外荷载是更复杂的非线性关系.本文给出了弹塑性全过程任意点的弯矩和挠度计算公式,可供结构设计者参考和应用. [1] 刘鸿文. 材料力学[M]. 北京: 高等教育出版社, 2010:76-89. [2] 聂国隽, 仲政. 用微分求积法求解梁的弹塑性问题[J]. 工程力学, 2005, 22(1): 59-62. [3] Kondoh K, Atluri S N. Large-deformation, elasto-plastic analysis of frames under nonconservative loading, using explicitly derived tangent stiffnesses based on assumed stresses[J]. Computational Mechanics, 1987, 2(1):1-25. [4] 曹天捷, 杜蓬娟. 一次超静定理想弹塑性梁的全过程分析[J]. 工程力学, 1999, 16(3): 105-112. [5] 李会知, 杨建中, 刘敏珊. 均布荷载作用下两端固支梁的弹塑性分析[J]. 河海大学学报:自然科学版, 2005, 33(4): 447-451. [6] 李会知, 刘敏珊, 陈淮. 一次超静定梁的弹塑性全过程分析[J]. 郑州大学学报:工学版, 2006, 27(2): 40-44. [7] 李会知, 刘敏珊, 陈淮. 均布荷载作用下一次超静定梁的弹塑性分析[J]. 工程力学, 2006, 23(10): 86-90. [8] 樊友景. 单跨均布荷载作用下两跨连续梁弹塑性分析[J]. 郑州大学学报:理学版, 2008, 40(4): 110-114. [9] 王仁, 黄文彬, 黄筑平. 塑性力学引论[M]. 北京: 北京大学出版社, 1992:53-55. [10]杨海波,曹建国,李洪波. 弹性和塑性力学简明教程[M]. 北京:清华大学出版社,2011:29-36. The Analysis of Entire Elastic-plastic Process of a Beam with One Degree of Indeterminacy under Uniformly-distributed Load LUO Yun-kuo1,2, LI Hui-zhi1 (1.SchoolofCivilEngineering,ZhengzhouUniversity,Zhengzhou450002,China;2.KaifengTongdaHighwayEngineeringCo.Ltd.,Kaifeng475003,China) The analysis of the entire elastic-plastic deformation process of a beam with one degree of indeterminacy under uniformly-distributed load was made. Based on the deformation feature, the up-loading process was divided into the following four stages : 1) the elastic stage, 2) the stage that beam region near the fixed end in plastic propagation state, 3) the stage that the fixed end as a plastic hinge while the plastic region near the end unloaded, and 4) the stage that the fixed end as a plastic hinge while the plastic region near the mid-point developing until the second plastic hinge occurring in the middle. In the first stage, the relationship between moment and load was proportional, so was that between deflection and the load. In the second stage, the relationship between moment and the load was complicated and nonlinear, so was that between deflection and the load. In the third stage, the relationship between moment and the load was linear but not proportion, so was that between deflection and the load. In the fourth stage, the relationship between moment and the load was the same as that in last stage, while the relationship between deflection and the load was much complicated and nonlinear. The formulae of moment and deflection of arbitrary point at each stage were derived. The formulas can be applied to engineering structure design. statically indeterminate beam; elastic-plastic; plastic hinge; uniformly-distributed load; deflection 2014-11-16 罗运阔(1974-),男,河南开封人,学士,主要从事土木工程研究,E-mail:luoyunkuo@163.com;通讯作者:李会知(1965-),男,河南永城人,教授,博士,主要从事结构分析研究,E-mail:lhz6380@zzu.edu.cn. TU323.3 A 1671-6841(2015)01-0119-06 10.3969/j.issn.1671-6841.2015.01.026


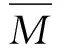

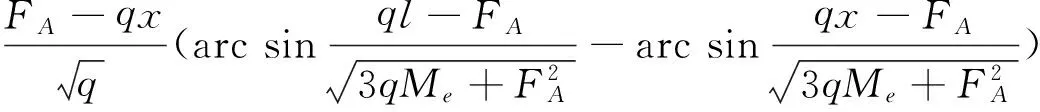




3 固支端保持为塑性铰而固支端附近塑性变形区卸载阶段
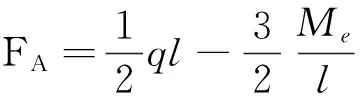




4 固支端保持为塑性铰而梁中部塑性变形区扩展阶段



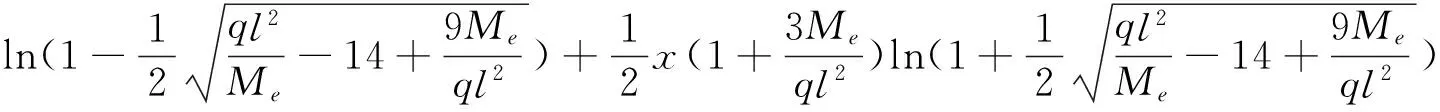









5 结束语
