一类非线性伪双曲方程Hermite型有限元的超收敛分析和外推
2015-02-11毛凤梅王俊俊
毛凤梅, 刁 群, 王俊俊
(平顶山学院 数学与信息科学学院 河南 平顶山 467000)
一类非线性伪双曲方程Hermite型有限元的超收敛分析和外推
毛凤梅, 刁 群, 王俊俊
(平顶山学院 数学与信息科学学院 河南 平顶山 467000)
在半离散格式下讨论了一类非线性伪双曲方程的Hermite型矩形元逼近. 利用插值理论、高精度分析和平均值技巧,借助于插值后处理技术,导出了精确解u的H1模意义下O(h3)阶的超逼近性质和整体超收敛. 进一步,通过构造一个适当的辅助问题,运用Richardson外推格式,得到了更高精度O(h4)阶的外推结果.
非线性伪双曲方程; 超逼近和超收敛; Hermite型矩形元; 外推
0 引言
考虑如下一类非线性伪双曲方程:
(1)
其中,Ω为R2上的一个有界闭区域,∂Ω为其光滑边界,X=(x,y).u0(X),u1(X),g(X,t)是已知光滑函数,f(u),a(u),b(u)满足有界函数且关于u满足Lipschitz条件.
伪双曲问题[1]是人们在研究非线性连续动力系统,动物神经轴突中的生物传导过程或黏弹性理论中提出的,这类方程的特点是含有时间和空间的高阶混合偏导数,对它的研究具有重要的理论价值与实际意义.文献[2-3]利用H1-Galerkin混合有限元方法对其进行了收敛性分析;文献[4]利用类Wilson元对其进行了超收敛性分析. 超收敛性和外推是提高有限元解的精度的有效方法,文献[5]构造了新的非常规Hermite型矩形元,并且对二阶椭圆方程导出了超收敛及外推结果;文献[6-7]分别讨论了Sine-Gordon方程和黏弹性方程的Hermite型元的高精度分析及超收敛性和外推. 本文主要目的是讨论非线性伪双曲方程的非常规Hermite型矩形元的超逼近及超收敛分析和外推,利用积分恒等式、平均值理论和插值后处理技术,得到了H1模意义下O(h3)阶的超逼近结果. 最后,通过构造一个适当的外推格式,导出了O(h4)阶的外推结果.
1 单元构造及引理
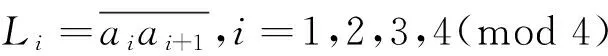
在K上定义有限元(K,Pk,∑k)如下:
Pk=span{1,x,y,xy,x2,y2,x2y,xy2},

设Ih:H2(Ω)→Vh为其诱导出的插值算子,文献[5]已验证该插值算子适定,并有引理1.


(2)
变分问题(2)有限元逼近方程为:求uh∈Vh,使得∀v∈Vh,有
(3)
由微分方程解的存在唯一性定理[8]知,方程(3)存在唯一解.
2 超逼近和超收敛分析
基于上述引理,给出下面的超逼近分析:


证明令u-uh=(u-Ιhu)+(Ιhu-uh)=η+θ,∀v∈Vh,由式(2),(3)得
(θtt,v)+(a(uh)θt,v)+(b(uh)θ,v)=
((f(u)-f(uh))ut,v)+(f(uh)θt,v)+(f(uh)ηt,v)-(ηtt,v)-
(α(uh)ηt,v)-((a(u)-a(uh))ut,v)-(b(uh)η,v)-
((b(u)-b(uh))u,v).
(4)
令v=θt代入式(4),则
((b0-b(uh))θ,θt)+((f(u)-f(uh))ut,θt)+(f(uh)θt,θt)+(f(uh)ηt,θt)-(ηtt,θt)-
((a(uh)-a(u))ηt,ηt,ηt,θt)-
((a(u)-a(uh))ut,θt)-((b(uh)-b(u))η,η,θt)-
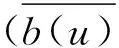

(5)
两边对t积分,并注意到θ(X,0)=θt(X,0)=0,再由Gronwall引理可得
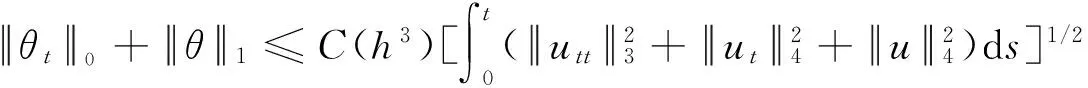
(6)


3 外推
设网格剖分是均匀的(记hx,K=hx,hy,K=hy),根据文献[5,7],有下面的引理2,3.
引理2[7]∀u∈H4(Ω),v∈Vh,则有

引理3[5]∀u∈H5(Ω),v∈Vh,则有


基于上面的引理,有定理3.
定理3设u,ut∈H5(Ω),utt∈H4(Ω)则

证明根据方程(4)和引理2,3得
(θtt,v)+(a(uh)θt,v)+(b(uh)θ,v)=
((f(u)-f(uh))ut,v)+((f(uh))θt,v)+((f(uh))ηt,v)-((a(uh)-a(u))ηt,v)-


(7)
考虑辅助问题,
(8)
其中,L(v)=L1(v)+L2(v)+L3(v).
类似于式(5)的估计得,
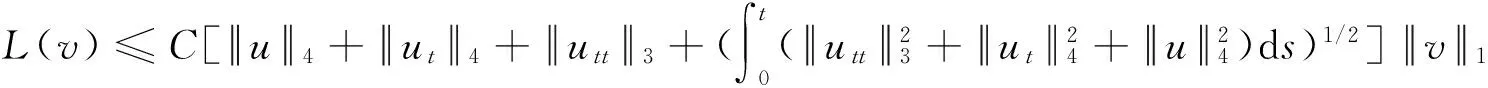



问题(8)的有限元逼近问题为
(9)
由式(7)得
(θtt,v)+(a(uh)θt,v)+(b(uh)θ,v)=

(10)
由式(9)、(10)得


(11)
((b0-b(uh))ξ,

两边从0到t积分,并注意到ξ(X,0)=ξt(X,0)=0,再由Gronwall引理得
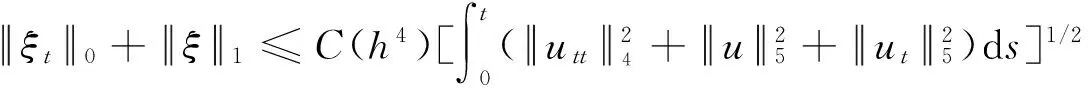
把相邻的16个Th的小单元格合并构成的1个大单元格,类似于文献[5]中构造的插值后处理算子4h,则成立如下的外推结果:1=O(h4).
注:本文的超逼近和超收敛结果对Hermite型三角形元亦成立.
[1] Pao C V. A mixed initial boundary-value problem arising in neurophysiology[J]. J Math Anal Appl,1975, 52(1): 105-119.
[2] Shi D Y,Zhang Y D.AnH1-Galerkin mixed finite element methods for pseudo-hyperbolic equations[J]. Math Appl,2011,24(3): 448-455.
[3] Wang J F, Liu Y, Li H, et al. AnH1-Galerkin expanded mixed element method for semi-linear hyperbolic wave equation[J].Chin Quart J of Math,2013, 28(1): 60-68.
[4] 史艳华,石东洋.伪双曲方程类Wilson 非协调元逼近[J]. 山东大学学报:理学版,2013, 48(4): 77-84.
[5] 石东洋,梁慧. 一个新的非常规Hermite 型各向异性矩形元的超收敛分析及外推[J]. 计算数学,2005,27(4): 369-382.
[6] 王芬玲.石东洋.非线性Sine-Gordon 方程Hermite 型有限元新的超收敛分析及外推[J]. 应用数学学报,2012,35(5): 777-787.
[7] 史艳华,石东洋.粘弹性方程Hermite 型有限元新的超收敛分析及外推[J]. 河南师范大学学报:自然科学版,2009,32(6): 148-151.
[8] Hale J K. Ordinary Differential Equations[M]. New York: Wiley-Inter Science, 1969.
A New Superconvergence Analysis and Extrapolation of Hermite-type Finite Element for Nonlinear Pseudo-hyperbolic Equation
MAO Feng-mei, DIAO Qun, WANG Jun-jun
(SchoolofMathematicsandInformationScience,PingdingshanUniversity,Pingdingshan467000,China)
A Hermit-type rectangular element approximation was discussed for a class of nonlinear pseudo-hyperbolic equation under semi-discrete scheme. The superclose properties and the global superconvergence with orderO(h3) for the exactuinH1norm were obtained through interpolated post-processing approach. Furthermore, by constructing a suitable auxiliary problem, the extrapolation solution with orderO(h4) was deduced through Richardson scheme.
pseudo-hyperbolic equation; Hermite-type rectangular element; superclose and superconvergence; extrapolation
2014-11-12
国家自然科学基金资助项目,编号11271340.
毛凤梅(1965-),女,河南鲁山人,副教授,主要从事有限元方法及应用研究,E-mail: maofengmei@pdsu.edu.cn;通讯作者:刁群(1979-),女,河南夏邑人,讲师,硕士,主要从事有限元方法及应用研究,E-mail:diaoqun.happy@163.com.
O242.21
A
1671-6841(2015)01-0006-04
10.3969/j.issn.1671-6841.2015.01.002
