斜交板梁桥的横向受力理论计算与试验分析

马占海

（河北承德承秦高速公路管理处 承德 067000）

目前，正交简支梁桥的横向分布系数的简化计算方法有：杠杆原理法、偏心压力法、铰接板（梁）法、刚接法、比拟正交异性板法［1－2］等。对于一座由多片梁组成的梁桥，当桥上有荷载P作用时，由于结构的横向联系使荷载P在纵向（x）和横向（y）内同时发生传递，并使所有主梁都不同程度参与受力，随着荷载位置的变化，主梁所承担的荷载也随之变化。为分析方便，通常将空间问题简化为平面问题，即

S ＝Pη（x，y）≈Pη1（x）η2（y） （1）

式中：η（x，y）为空间计算某梁的内力影响面；η1（x）为单梁在x轴方向某一界面的内力影响线；η2（y）为某梁的荷载横向分布影响线。

但是斜交简支梁桥荷载效应横向分布的计算方法在使用上还不是很方便［3－5］，因此有必要建立空间计算模型对斜交简支梁桥各片梁的受力性能进行讨论。本文以某实际简支空心梁桥为例，分别利用空间有限元和现场荷载试验，探讨了斜交板梁桥的空间受力性能和荷载效应在横桥向的分布规律。

1 斜板桥空间受力性能

理论和实验证明，简支斜板桥在垂直荷载下有向两支承边最短距离方向传递的趋势。本文就不同倾斜程度的斜板桥，建立了空间有限元模型，讨论了垂直荷载下，荷载效应的传递规律。模型中每片梁宽为1.2m，共9片梁，跨径为20m，倾角分别为0°，30°，45°，60°，1号梁跨中截面在单位荷载作用下的弯矩场，见图1a），c），e），g）相应的各片梁最大弯矩的位置图，见图1b），d），f），h）。

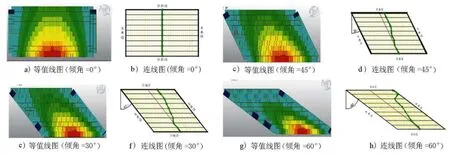
图1 1号梁跨中截面等值线图例

由图1可见，倾角分别为0°，30°，45°，60°的简支梁桥，当单位荷载作用在1号梁跨中截面时，荷载的横向传递趋势随斜交角度的变化而变化；各片梁的跨中位置连线与其所受的最大弯矩位置连线的分离程度随斜交角度的增大而增大。

2 实桥验证

某斜交简支板梁桥的计算跨径为19.6m，桥宽12.5m。上部结构采用先张预应力混凝土空心板梁，每孔由9片梁组成，梁宽为1.2m，梁高0.9m。设计荷载为汽－超20级，挂－120；横断面布置为0.5m（防撞护栏）＋11.5m（行车道）＋0.5m（防撞护栏），见图2。桥面铺装为10cm厚防水混凝土＋8cm沥青混凝土，混凝土强度为C50，斜交角度为60°。

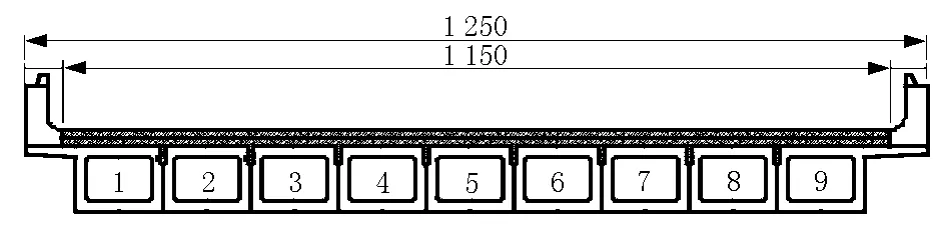
图2 横截面图（单位：cm）

2.1 试验荷载及控制截面

为讨论荷载效应的分布，选用1辆350kN重车作为试验荷载，加载车尺寸及轴重见图3。常规荷载试验一般是把B截面作为控制截面。本文依据上述分析提出将b截面作为控制截面。控制截面及加载车位置见图4。

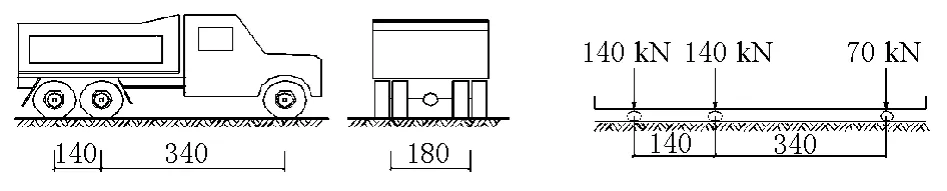
图3 加载车重量及尺寸（单位：cm）

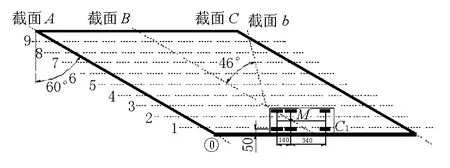
图4 控制截面及加载位置（单位：cm）

2.2 挠度测点

沿第1跨跨端A，C截面、跨中B截面以及从3号梁开始偏离B截面46°的b截面，布置挠度测点。测量时采用电阻式位移计进行测试，具体挠度测点布置见图5。

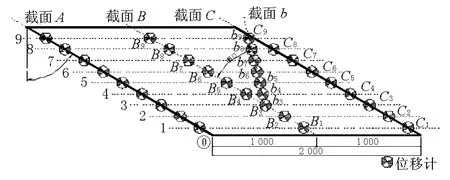
图5 挠度测点布置图（单位：cm）

2.3 测试结果分析

试验所得到的各梁挠度见表1，将挠度定义为向下为负，所得结果见图6。

表1 试验荷载下各梁挠度横向分布检测结果 mm

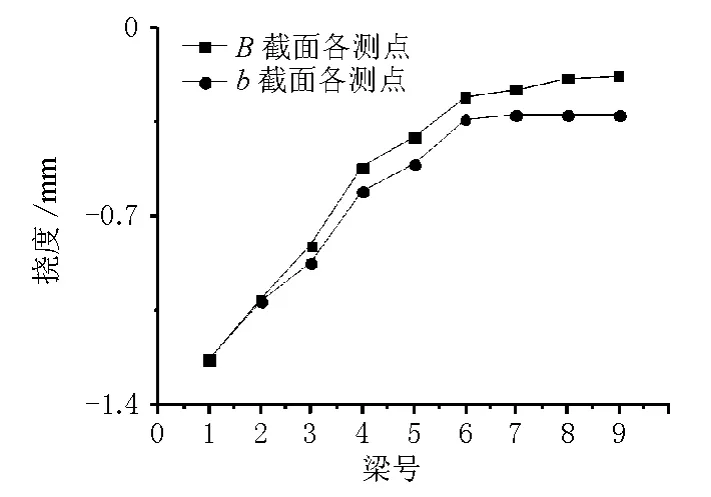
图6 试验荷载下各梁挠度横向分布结果对比图

由表1和图6可见，在试验荷载作用下，横向传递受斜交角的影响很大，不容忽略。距离荷载作用位置越远的主梁，其最大挠度出现的位置距离跨中也越远。

3 结论

（1）装配式简支斜交空心板梁桥在垂直荷载下有向两支承边最短距离方向传递的趋势。

（2）在对斜桥进行设计或检测评定过程中，应通过空间有限元分析模型分析倾角对荷载横向传递的影响，以减小利用简化的横向分布系数方法所带来的偏差。

［1］ 姚玲森.桥梁工程［M］.北京：人民交通出版社，2004.

［2］ 谢开仲，曾倬信，王晓燕.桥梁工程检测技术研究［J］.广西大学学报：自然科学版，2003，28（S1）：208－211.

［3］ 余钱华，于 强.斜交空心板桥横向分布系数计算方法研究［J］.公路与汽运，2013（3）：171－173.

［4］ 穆永江.简支空心板桥的荷载横向分布特性研究［D］.长春：吉林大学，2012.

［5］ 郑熙龙，李静辉，孙全胜.基于空心板桥的横向分布系数研究［J］.低温建筑技术，2013（10）：67－69.