STABILITY OF SOME POSITIVE LINEAR OPERATORS ON COMPACT DISK∗

Department of Mathematics,Aligarh Muslim University,Aligarh 202002,India

E-mail:mursaleenm@gmail.com;ansari.jkhursheed@gmail.com;asifjnu07@gmail.com

STABILITY OF SOME POSITIVE LINEAR OPERATORS ON COMPACT DISK∗

M.MURSALEENKhursheed J.ANSARIAsif KHAN

Department of Mathematics,Aligarh Muslim University,Aligarh 202002,India

E-mail:mursaleenm@gmail.com;ansari.jkhursheed@gmail.com;asifjnu07@gmail.com

Recently,Popa and Ra¸sa[27,28]have shown the(in)stability of some classical operators defned on[0,1]and found best constant when the positive linear operators are stable in the sense of Hyers-Ulam.In this paper we show Hyers-Ulam(in)stability of complex Bernstein-Schurer operators,complex Kantrovich-Schurer operators and Lorentz operators on compact disk.In the case when the operator is stable in the sense of Hyers and Ulam,we fnd the infmum of Hyers-Ulam stability constants for respective operators.

Hyers-Ulam stability;Bernstein-Schurer operators;Kantrovich-Schurer opera

tors;Lorentz operators;stability constants

2010 MR Subject Classifcation39B82;41A35;41A44

1 Introduction

The equation of homomorphism is stable if every“approximate”solution can be approximated by a solution of this equation.The problem of stability of a functional equation was formulated by S.M.Ulam[35]in a conference at Wisconsin University,Madison in 1940:“Given a metric group(G,.,ρ),a number ε＞0 and a mapping f:G→G which satisfes the inequality ρ(f(xy),f(x)f(y))＜ε for all x,y∈G,does there exist a homomorphism a of G and a constant k＞0,depending only on G,such that ρ(a(x),f(x))≤kε for all x∈G?”If the answer is afrmative the equation a(xy)=a(x)a(y)of the homomorphism is called stable;see[10,17].The frst answer to Ulam’s problem was given by D.H.Hyers[16]in 1941 for the Cauchy functional equation in Banach spaces,more precisely he proved:“Let X,Y be Banach spaces,ε a nonnegative number,f:X→Y a function satisfying‖f(x+y)-f(x)-f(y)‖≤ε for all x,y∈X, then there exists a unique additive function with the property‖f(x)-a(x)‖≤ε for all x∈X.”Due to the question of Ulam and the result of Hyers this type of stability is called today Hyers-Ulam stability of functional equations.A similar problem was formulated and solved earlier by G.P´olya and G.Szeg¨o in[25]for functions defned on the set of positive integers.After Hyers result a large amount of literature was devoted to study Hyers-Ulam stability for various equations.A new type of stability for functional equations was introduced by T.Aoki[2]and Th.M.Rassias[29]by replacing ε in the Hyers theorem with a function depending on x and y, such that the Cauchy diference can be unbounded.The results of Aoki and Rassias have beencomplemented later in the papers[12]and[7].Moreover,a lot of useful recent information on that type of stability can be found in[6].

The Hyers-Ulam stability of linear operators was considered for the frst time in the papers by Miura,Takahasi et al.(see[14,15,21]).Similar type of results are obtained in[34]for weighted composition operators on C(X),where X is a compact Hausdorfspace.A result on the stability of a linear composition operator of the second order was given by J.Brzdek and S.M.Jung in[9].

Recently,Popa and Ra¸sa obtained[26]a result on Hyers-Ulam stability of the Bernstein-Schnabl operators using a new approach to the Fr´echet functional equation,and in[27,28], they have shown the(in)stability of some classical operators defned on[0,1]and found the best constant for the positive linear operators in the sense of Hyers-Ulam.For other results on the Hyers-Ulam stability of functional equations one can refer to[22,23].

Motivated by their work,in this paper,we show the(in)stability of some complex positive linear operators on compact disk in the sense of Hyers-Ulam.We fnd the infmum of the Hyers-Ulam stability constants for complex Bernstein-Schurer operators and complex Kantrovich-Schurer operators on compact disk.Further we show that Lorentz polynomials are not stable in the sense of Hyers-Ulam on a compact disk.Issues considered in this paper are strictly connected with the problems of stability of the equation of fxed point investigated in[30]. Also,some related results have been obtained in[4,5,24,31,32,36]and[8].

2 The Hyers-Ulam Stability Property of Operators

In this section,we recall some basic defnitions and results on Hyers-Ulam stability property which form the background of our main results.

Defnition 2.1(see[34])Let A and B be normed spaces and T a mapping from A into B.We say that T has the Hyers-Ulam stability property(briefy,T is HU-stable)if there exists a constant K such that:

(i)for any g∈T(A),ε＞0 and f∈A with‖Tf-g‖≤ε,there exists an f0∈A such that Tf0=g and‖f-f0‖≤Kε.The number K is called a HUS constant of T,and the infmum of all HUS constants of T is denoted by KT.Generally,KTis not a HUS constant of T(see [14]and[15]).

Theorem 2.2(see[34])Let A and B be Banach spaces and T:A→B be a bounded linear operator.Then the following statements are equivalent:

(a)T is HU-stable;

(b)R(T)is closed;

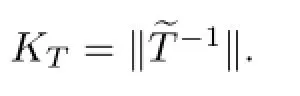
Remark 2.3(1)Condition(i)of Defnition 2.1 expresses the Hyers-Ulam stability of the equation Tf=g,where g∈R(T)is given and f∈A is unknown.

(2)If T:A→B is a bounded linear operator,then(i)is equivalent to:

(ii)for any f∈A with‖Tf‖≤1 there exists an f0∈N(T)such that‖f-f0‖≤K(see [13]).

The main results used in our approach for obtaining,in some concrete cases,the explicit value of KTare the formula given above and a result by Lubinsky and Ziegler[19]concerning coefcient bounds in the Lorentz representation of a polynomial.Let P∈Πn,where Πnis the set of all polynomials of degree at most n with real coefcients.

A Lorentz representation of a polynomial P(x),is a representation of the form

where ck∈R,k=0,1,···,n.While it is not unique in general-for example

-it becomes unique if we insist in(2.1)that n equals the degree of P.

Note that,in fact,it is a representation in Bernstein-B´ezier basis.Let Tndenote the usual n-th degree Chebyshev polynomial of the frst kind.From the expressions given in([11],p.34), one readily derives the representation:

where

It is proved in[27]that

Therefore

Theorem 2.4(Lubinsky and Ziegler[19])Let P(x)have the representation(2.1),and let 0≤k≤n.Let dn,kbe defned by(2.3).Then

with equality if and only if P(x)is a constant multiple of Tn(2x-1),where

As in[19],we observe that

Let A be the Banach space and M the closed subspace of A,then by A/M,we denote the quotient space with the usual norm

For more details,one can refer to[14].

Let C[0,1]be the space of all continuous,real-valued functions defned on[0,1],and CB[0,+∞)the space of all continuous,bounded,real-valued functions on[0,+∞).Endowed with the supremum norm,they are Banach spaces.

Popa and Ra¸sa have shown the Hyers-Ulam stability of the following operators:

(i)Bernstein operators[27]

For each integer n≥1,the sequence of classical Bernstein operators Bn:C[0,1]→C[0,1] is defned by(see[1])

They are stable in the Hyers-Ulam sense and the best Hyers-Ulam stability constant is given by

(ii)Sz´asz-Mirakjan operators[27]

The nth Sz´asz-Mirakjan operator Ln:Cb[0,+∞)→Cb[0,+∞)defned by(see[1],pp. 338)

is not HU-stable for each n≥1.

(iii)Beta operators[27]

For each n≥1,the Beta operator Bn:C[0,1]→C[0,1]defned by[20]

is not stable in the sense of Hyers-Ulam.

(iv)Stancu operators[28]

Let C[0,1]be the linear space of all continuous functions f:[0,1]→R,endowed with the supremum norm denoted by‖.‖,and a,b real numbers,0≤a≤b.The Stancu operator[33] Sn:C[0,1]→Πnis defned by

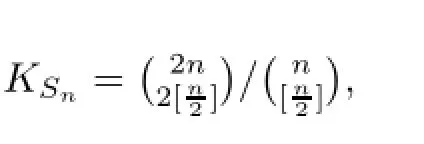
(v)Kantorovich operators[28]

Let X={f:[0,1]→R:where f is bounded and Riemann integrable}be endowed with the supremum norm denoted by‖.‖.The Kantorovich operators defned by

3 Main Results

In this section,we show the Hyers-Ulam stability of some other operators.Let DRdenote the compact disk having radius R,i.e.,DR={z∈C:|z|≤R}.

(i)Bernstein-Schurer Operators

Let XDR={f:DR→C|f is analytic in DR}be the collection of all analytic functions endowed with the supremum norm denoted by‖.‖for f∈XDR.The supremum norm is not over the whole space(as it is usually understood)and that the dimension of Πn+mis over reals. The complex Bernstein-Schurer operator Sn,m:XDR→Πn+mis defned by(see[3])

Theorem 3.1For n≥1,the Hyers-Ulam stability best constant(by Defnition 2.1 and Theorem 2.2)is given by

ProofLet p(z)∈Πn+mand‖p‖≤1.The Lorentz representation of p(z)is given by

Consider the constant function fp∈XDRdefned by

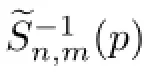
Hence using the above equality,we have

On the other hand,let r(z)=Tn(2z-1),|z|≤R.Then‖r‖=1 and|ck(r)|=dn+m,k, 0≤k≤n+m,according to Theorem 2.4.Consequently by(3.1),we have

and so by(3.2)and(3.3),we obtain

This completes the proof of the theorem.

(ii)Kantrovich-Schurer Operators

Let XDR={f:DR→C is analytic in DR}be the collection of all analytic functions endowed with the supremum norm denoted by‖.‖.The complex Kantrovich-Schurer operator [3]Kn,m:XDR→Πn+mis defned by

We have

The operators Kn,mare Hyers-Ulam stable since their ranges are fnite dimensional spaces.

Theorem 3.2For n≥1

ProofLet p(z)∈Πn+m,‖p‖≤1,and its Lorentz representation

Consider the constant function fp∈XDRdefned by

On the other hand,let r(z)=Tn(2z-1),|z|≤R.Then‖r‖=1 and|ck(r)|=dn+m,k, 0≤k≤n+m,according to Theorem 2.4.Consequently by(3.4),we have

and so by(3.5)and(3.6),we can conclude

This completes the proof of the theorem.

(iii)Lorentz Operators

The complex Lorentz polynomial[13]attached to any analytic function f in a domain containing the origin is given by

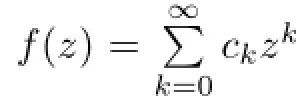
Theorem 3.3For each n≥1,the Lorentz polynomial on compact disk is not stable in the sense of Hyers and Ulam.

ProofTo prove this theorem,we use the approach used in[27,Theorem 4.1].Let us denote ej(z)=zj,then from Lorentz operators we can easily obtain that Ln(e0)(z)=1, Ln(e1)(z)=e1(z);and for all j,n∈N,j≥2,we have

Also an easy computation shows that

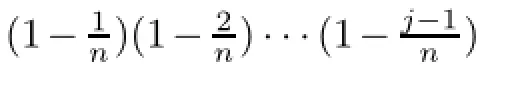
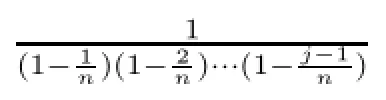
This completes the proof of the theorem.

[1]Altomare F,Campiti M.Korovkin-Type Approximation Theory and its Applications.Berlin,New York: W de Gruyter,1994

[2]Aoki T.On the stability of linear transformation in Banach spaces.J Math Soc Japan,1950,2:64-66

[3]Anastassiou G A,Gal S G.Approximation by complex Bernstein-Schurer and Kantorovich-Schurer polynomials in compact disks.Comput Math Appl,2009,58:734-743

[4]Bota M,Karapinnar E,Mle¸snit¸e O.Ulam-Hyers stability results for fxed point problems via α-ψ-contractive mapping in(b)-metric space.Abstr Appl Anal,2013,Art ID 825293

[5]Bota M,Petru T P,Petru¸sel G.Hyers-Ulam stability and applications in guage spaces.Miskolc Math Notes, 2013,14(1):41-47

[6]Brillou¨et-Belluot N,Brzd¸ek J,Ciepli´nski K.On some recent developments in Ulam’s type stability.Abstr Appl Anal,2012,2012:Article ID 716936

[7]Brzd¸ek J.Hyperstability of the Cauchy equation on resticted domains.Acta Math Hungar,2013,141: 58-67

[8]Brzd¸ek J,C˘adariu L,Ciepli´nski K.Fixed point theory and the Ulam stability.J Function Spaces,2014, 2014:Article ID 829419

[9]Brzd¸ek J,Jung S M.A note on stability of an operator linear equation of the second order.Abstr Appl Anal,2011,15:Article ID 602713

[10]Brzd¸ek J,Rassias Th M.Functional Equations in Mathematical Analysis.Springer,2011

[11]Freud G.Orthogonal Polynomials.Budapest:Akademiai Kiado/Pergamon Press,1966

[12]Gajda Z.On stability of additive mappings.Int J Math Math Sci,1991,14:431-434

[13]Gal S G.Approximation by complex Lorentz polynomials.Math Commun,2011,16:67-75

[14]Hatori O,Kobayasi K,Miura T,Takagi H,Takahasi S E.On the best constant of Hyers-Ulam stability.J Nonlinear Convex Anal,2004,5:387-393

[15]Hirasawa G,Miura T.Hyers-Ulam stability of a closed operator in a Hilbert space.Bull Korean Math Soc, 2006,43:107-117

[16]Hyers D H.On the stability of the linear functional equation.Proc Natl Acad Sci,1941,27:222-224

[17]Hyers D H,Isac G,Rassias Th M.Stability of Functional Equation in Several Variables.Basel:Birkh¨auser, 1998

[18]Lorentz G G.Bernstein Polynomials.2nd ed.New York:Chelsea Publ,1986

[19]Lubinsky D S,Ziegler Z.Coefcients bounds in the Lorentz representation of a polynomial.Canad Math Bull,1990,33:197-206

[20]Lupa¸s A.Die Folge der Betaoperatoren[D].Univ Stuttgart,1972

[21]Miura T,Miyajima M,Takahasi S E.Hyers-Ulam stability of linear diferential operator with constant coefcients.Math Nachr,2003,258:90-96

[22]Mohiuddine S A,Mursaleen M,Ansari K J.On the stability of fuzzy set-valued functional equations. Scientifc World J,2014,Article ID 392943

[23]Mursaleen M,Ansari K J.Stability results in intuitionistic fuzzy normed spaces for a cubic functional equation.Appl Math Inform Sci,2013,7(5):1685-1692

[24]Petru¸sel A,Petru¸sel G,Urs C.Vector-valued metrics,fxed points and coupled fxed points for nonlinear operators.Fixed Point Theory Appl,2013,2013:218

[25]P´olya G,Szeg¨o G.Aufgaben und Lehrs¨atze aus der Analysis,I.Berlin:Springer,1925

[26]Popa D,Ra¸sa I.The Fr´echet functional equation with applications to the stability of certain operators.J Approx Theory,2012,164(1):138-144

[27]Popa D,Ra¸sa I.On the stability of some classical operators from approximation theory.Expo Math,2013, 31:205-214

[28]Popa D,Ra¸sa I.On the best constant in Hyers-Ulam stability of some positive linear operators.J Math Anal Appl,2014,412:103-108

[29]Rassias Th M.On the stability of the linear mappings in Banach spaces.Proc Amer Math Soc,1978,72: 297-300

[30]Rus I A.Remarks on Ulam stability of the operatorial equations.Fixed Point Theory,2009,10:305-320 [31]Rus I A.Ulam stability of operatorial equations//Functional Equations in Mathematical Analysis.New York:Springer,2012:287-305

[32]Sintunavarat W.Genaralized Hyers-Ulam stability,well-posedness,and limit showding of fxed point problems for α-β-contraction mapping in metric spaces.Scientifc World J,2014,Article ID 569174

[33]Stancu D D.Asupra unei generaliz˘ari a polinoamelor lui Bernstein.Stud Univ Babe¸s-Bolyai,1969,14: 31-45

[34]Takagi H,Miura T,Takahasi S E.Essential norms and stability constants of weighted composition operators on C(X).Bull Korean Math Soc,2003,40:583-591

[35]Ulam S M.A Collection of Mathematical Problems.New York:Interscience,1960

[36]Urs C.Ulam-Hyers stability for coupled fxed points of cntractive type operators.J Nonlinear Sci Appl, 2013,6(2):124-136

∗Received May 8,2014;revised October 2,2014.